7.7 随伴の別定義
1)別定義
随伴の定義にはこれまでと異なる方法がある。それは次のように定義される。
\(\fbox {随伴の定義2:}\)
二つの局所的に小さな圏\(\mathcal{C},\mathcal{D}\)において、関手の対\(R: \mathcal{C} \rightarrow \mathcal{D}, L: \mathcal{D} \rightarrow \mathcal{C}\)が次の条件を満たす時そしてその時に限り、随伴であるという。
\begin{eqnarray}
\mathcal{C} (L(Y),X) \cong \mathcal{D} (Y,R(X)) \\
\end{eqnarray}
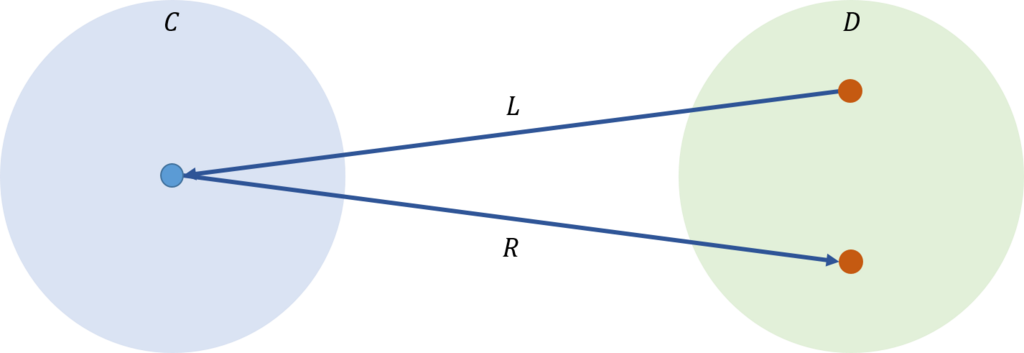
これを、下図に示す。

もう少し、詳しく説明しよう。
まず、定義をするための準備をしよう。今、二つの圏\(\mathcal{C},\mathcal{D}\)からそれぞれターゲットとなる対象\(X\)とソースとなる対象\(Y\)を適当に選んだとしよう。そして、ソースである対象\(Y\)を\(L\)によって、\(\mathcal{C}\)に写像したとしよう。これにより、二つの対象\(L(Y),X\)の間で、\({\rm Hom}\)集合\(\mathcal{C}(L(Y),X)\)を定義することができる。
同様にして、ターゲットである対象\(X\)を\(R\)によって、\(\mathcal{D}\)に写像したとしよう。これにより、二つの対象\(Y,R(X)\)の間で、\({\rm Hom}\)集合\(\mathcal{C}(Y,R(X))\)を定義することができる。
それでは随伴の定義をしてみよう。関手の対\(L,R\)が随伴の時かつその時に限り、二つの\({\rm Hom}\)集合\(\mathcal{C}(L(Y),X)\)と\(\mathcal{D}(Y,R(X)))\)は同型
\begin{eqnarray}
\mathcal{C}(L(Y),X) \cong \mathcal{D}(Y,R(X))
\end{eqnarray}
である。即ち、\(X,Y\)に対して自然である。
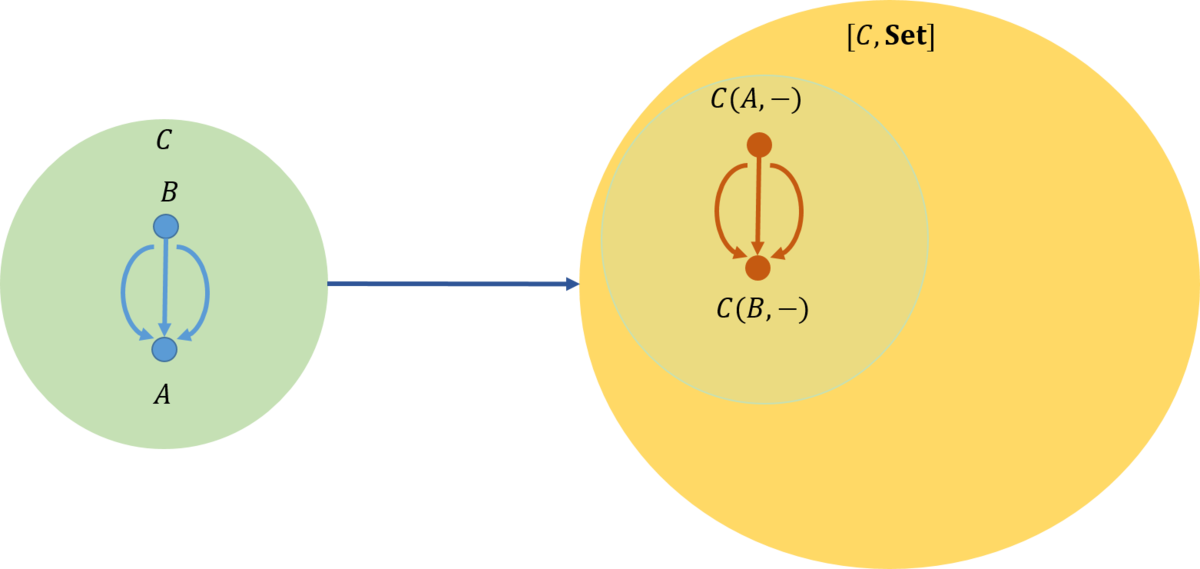
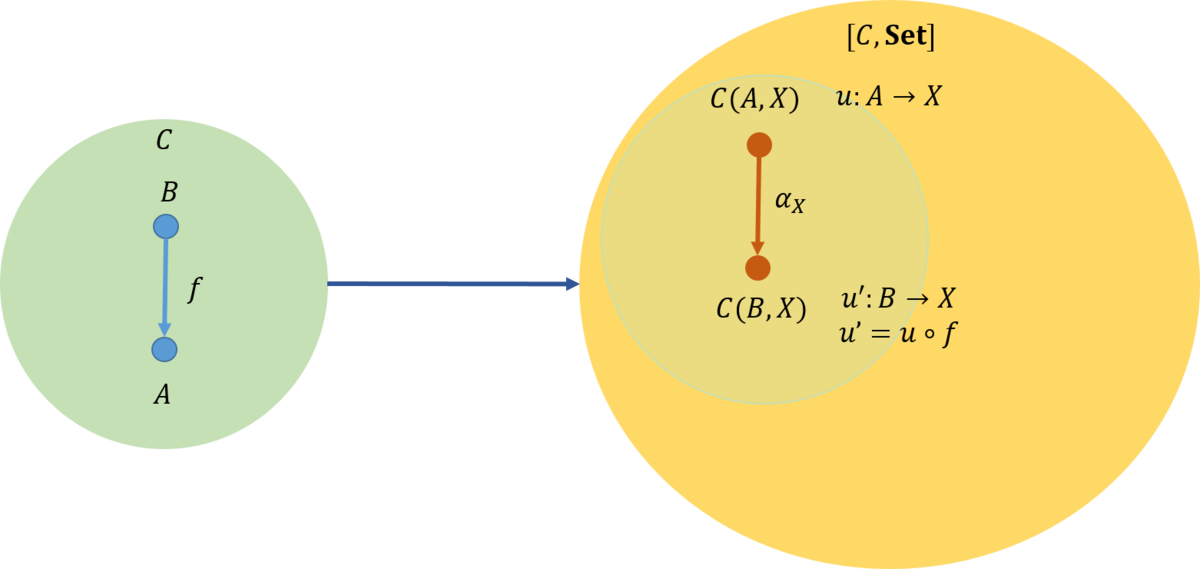
ここで、自然であるとは、\(\mathcal{C}\)から\({\rm Hom}\)集合の圏\({\rm Set}\)に対して、次の二つの関手
\begin{eqnarray}
X \rightarrow C(L(Y), X) \\
X \rightarrow D(Y, R(X))
\end{eqnarray}
の間に自然変換があり、さらに、
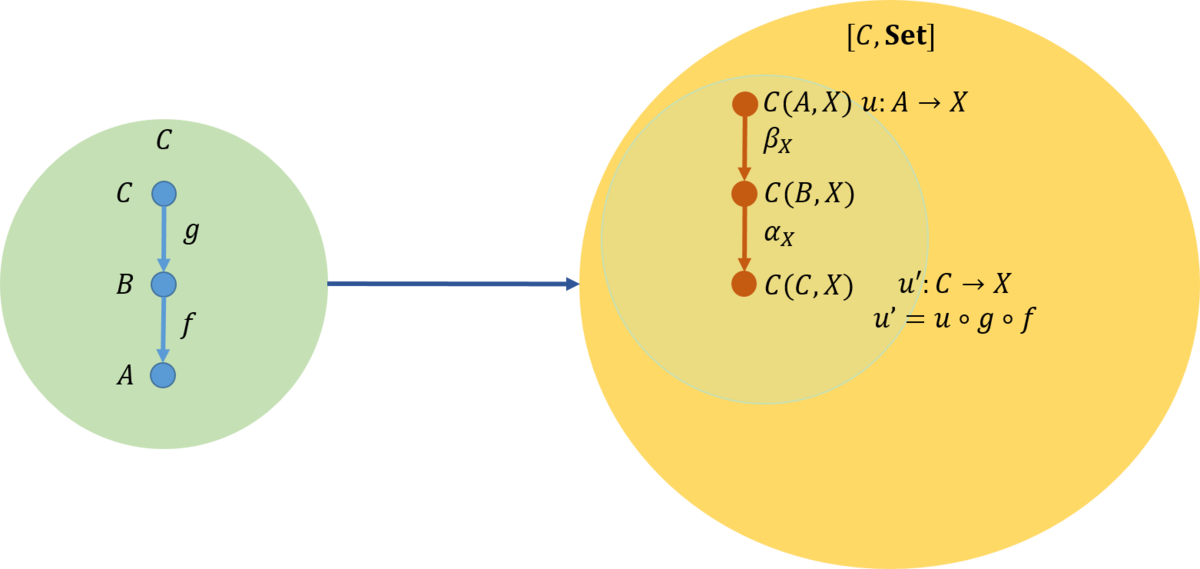
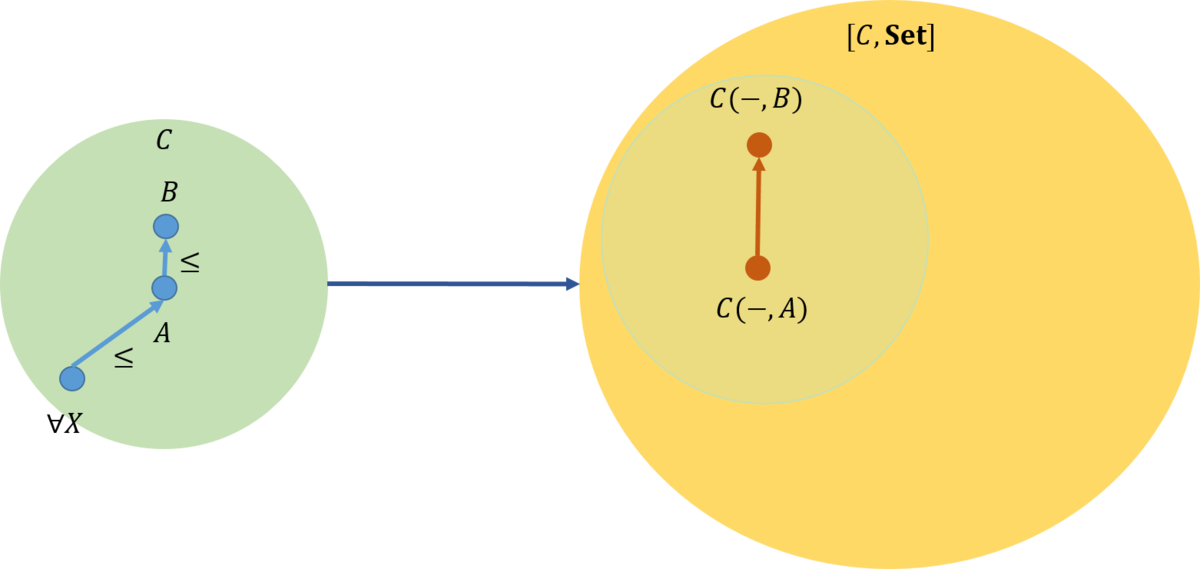
\(\mathcal{D}\)から\({\rm Hom}\)集合の圏\({\rm Set}\)に対して、次の二つの関手
\begin{eqnarray}
Y \rightarrow C(L(Y), X) \\
Y \rightarrow D(Y, R(X))
\end{eqnarray}
の間に自然変換があり、そして、自然変換は可逆(invertible)であることである。
これが、随伴の別定理である。
これと、今までに示してきた定義(下記に示す)が同一となる。
\(\fbox {随伴の定義1:}\)
二つの局所的に小さな圏\(\mathcal{C},\mathcal{D}\)において、関手の対\(R: \mathcal{C} \rightarrow \mathcal{D}, L: \mathcal{D} \rightarrow \mathcal{C}\)が三角恒等式を満たす次の射\(ϵ,η\)を有する時、随伴であるという。
\begin{eqnarray}
ϵ : L \circ R \rightarrow I_\mathcal{C} \\
η : I_\mathcal{D} \rightarrow R \circ L
\end{eqnarray}
それでは、二つの定義が同じであることの証明の概略を示そう。
2)証明の概略
定義2から定義1を導いてみよう。
同型は、任意の対象\(X\)に対して働くので、\(X=L(Y)\)としよう。そうすると、
\begin{eqnarray}
\mathcal{C}(L(Y), L(Y)) \cong \mathcal{C}(Y,R(L(Y))
\end{eqnarray}
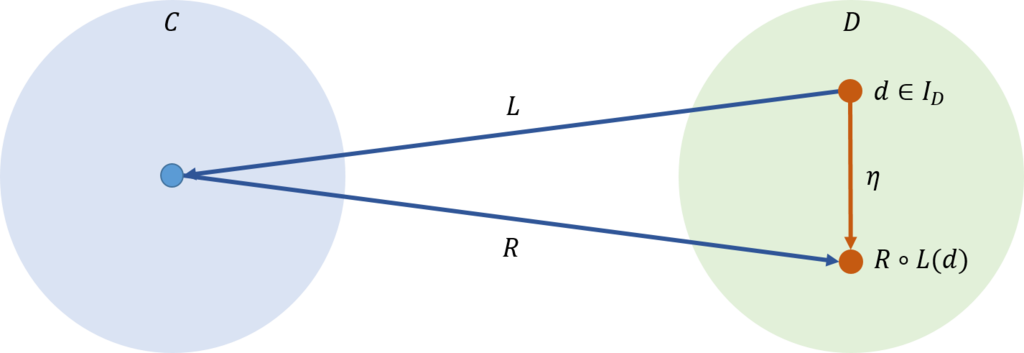
これより、左辺は少なくとも一つの射、即ち、恒等射\(I\)を持たなければならない。自然変換は恒等射を、\({\rm Hom}\)集合\(\mathcal{C}(Y,R(L(Y)))\)の一つの要素に写像する。ここで、\(I\)を挿入すると、\(\mathcal{C}(I(Y),R(L(Y)))\)の中の一つの要素にとなる。\(Y\)は任意なので、これは、まさしく、\(η : I_\mathcal{D} \rightarrow R \circ L\)と同じである。
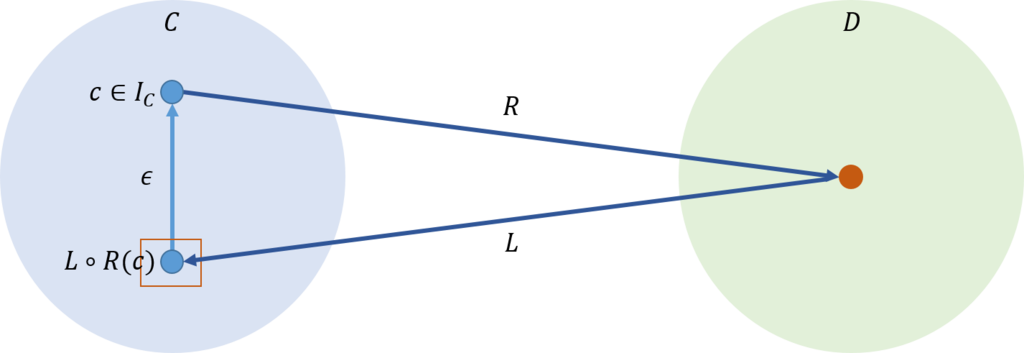
同じように、\(ϵ: L \circ R \rightarrow I_\mathcal{C}\)を得ることができる。
また、二つの自然変換、即ち、
\begin{eqnarray}
X \rightarrow C(L(Y), X) \\
X \rightarrow D(Y, R(X))
\end{eqnarray}
と
\begin{eqnarray}
Y \rightarrow C(L(Y), X) \\
Y \rightarrow D(Y, R(X))
\end{eqnarray}
が可逆であることから三角恒等式を導くことができる。
逆に定義1から定義2も導いてみよう。
ここでは、片方(\(\mathcal{C}(L(Y),X)\)または\(\mathcal{D}(Y,R(X))\))の射が定まった時に他方(\(\mathcal{D}(Y,R(X))\)または\(\mathcal{C}(L(Y),X)\))の射が一意的に定まることを示せばよい。
そこで、\(f\)を\(\mathcal{C}(L(Y),X)\)の任意の射としてみよう。これを関手\(R\)を用いて\(\mathcal{D}\)上に持ち上げると、
\begin{eqnarray}
R \circ f : R(L(Y)) \rightarrow R(X)
\end{eqnarray}
となる。
そこで、随伴の定義1での射\(η\)を用いると
\begin{eqnarray}
η: I_D \rightarrow R \circ L \\
η_X: I_D(Y) \rightarrow R \circ L (Y) \\
η_X: Y \rightarrow R \circ L (Y)
\end{eqnarray}
を得る。
従って、
\begin{eqnarray}
R \circ f \circ η_X: Y \rightarrow R (X)
\end{eqnarray}
となる。\(\phi_x = R \circ f \circ η_X\)とすると、
\begin{eqnarray}
\phi_X: Y \rightarrow R (X)
\end{eqnarray}
が一意に定まることが分かる。
同様に、\(\mathcal{D}(Y,R(X)\)の任意の射に対しても、\(\mathcal{C}(L(Y),X)\))の射が一意的に定まることが分かる。そして、三角恒等式を利用して、二つの自然変換が可逆となることを示すことができる。
これにより同型であること、即ち、
\begin{eqnarray}
\mathcal{C}(L(Y),X) \cong \mathcal{D}(Y,R(X))
\end{eqnarray}
を導くことができる。