8.随伴関手の応用
圏論の創始者はソーンダース・マックレーン(Saunders Mac Lane)とサミュエル・アイレンベルグ(Samuel Eilenberg)だ。1942年から45年にかけて、代数的位相幾何学(Algebraic Topology)を研究する中で、関手や自然変換などの圏論の概念を生み出した。マックレーンの著書“Categories for Working Mathematician”の冒頭で、彼は、”Adjoint functors arise everywhere.”と言っている。意訳すると、どこもかしこも随伴関手だらけということだろう。彼の考え方に従えば、殆どのことは随伴関手を用いて記述できるということだ。そこで、今回の記事では、これまでに学んできた普遍性の中からいくつか取り上げて、随伴関手を用いて表すこととしよう。
なお、マクレーンは、修士課程までをアメリカで学び、物足りなかったのだろう、当時、世界の最高峰の大学と目されていたドイツのゲッティンゲン大学で博士課程を過ごす。その後、米国に戻り、シカゴ大学教授となる。とても長生きをし、2005年に95歳で亡くなった。アイレンベルグはポーランド出身、ワルシャワ大学で博士号を修得した後、コロンビア大学の教授となった。彼も長生きしたほうだろう、1998年に84歳で亡くなっている。
8.1 自然変換の合成
随伴関手の中で、自然変換が重要な役割をなすので、自然変換の構成について簡単に説明しておこう。
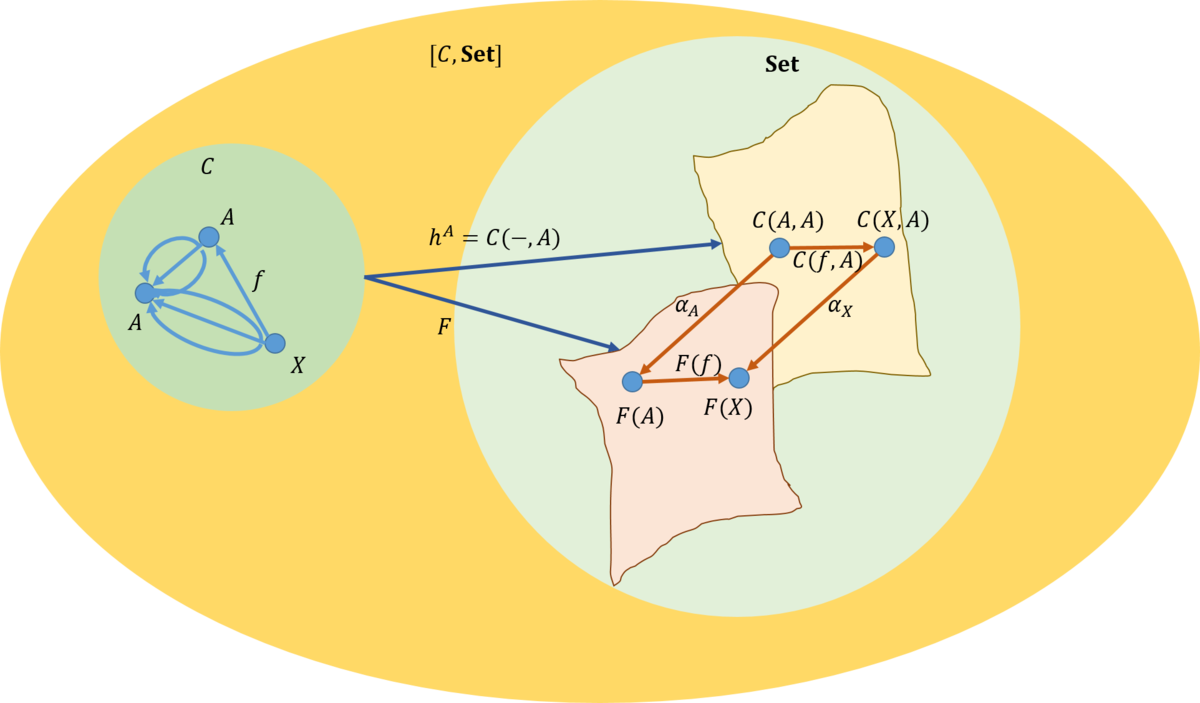
自然変換は、関手から関手への射である。自然変化の合成は、関手を介在させた縦方向の合成と

圏を介在させた横方向の合成がある。

ここでは横方向の合成について考えよう。縦方向については読者の方で考えて欲しい。
それでは、上の図での自然変換の合成
\begin{eqnarray}
\beta \circ \alpha : G \circ F \rightarrow G’ \circ F’
\end{eqnarray}
を考えることとしよう。
自然変換は、成分ごとに考えればよい。そこで、圏\(\mathcal{A}\)と圏\(\mathcal{B}\)の対象を\(X\)と\(Y\)としよう。

これより
\begin{eqnarray}
\alpha (X) : F(X) \rightarrow F’ (X) \\
\beta (X) : G(X) \rightarrow G’ (X)
\end{eqnarray}
となる。従って、
\begin{eqnarray}
(\beta \circ \alpha) (X) : G \circ F (X) \rightarrow G’ \circ F’ (X)
\end{eqnarray}
となり、さらに
\begin{eqnarray}
G \circ \alpha (X) : G \circ F (X) \rightarrow G \circ F’ (X)
\end{eqnarray}
である。
これより、
\begin{eqnarray}
(\beta \circ \alpha) (X) : G \circ F (X) \rightarrow G \circ F’ (X) \rightarrow G’ \circ F’ (X)
\end{eqnarray}
となり、
\begin{eqnarray}
(\beta \circ \alpha) (X) = \beta (F’ (X)) \circ (G \circ \alpha (X))
\end{eqnarray}
を得る。
これで、自然変換の合成を得ることができたが、それでは、その性質をいくつか調べてみよう。まず、\(\alpha=Id\)の場合を考えてみよう。即ち、\(Id : F \rightarrow F\)の場合である。

\begin{eqnarray}
(\beta \circ F) (X) & = &\beta (F’ (X)) \circ (G \circ \alpha (X)) \\
& = & \beta (F’ (X)) \circ (G \circ Id (X)) \\
& = & \beta (F’ (X))
\end{eqnarray}
上記で、\(G \circ Id (X)\)は恒等射\( Id (X)\)に関手\(G\)を適応させたものであるので、恒等射となる。
次に、\(\beta=Id\)の場合を考えてみよう。即ち、\(Id : G \rightarrow G\)の場合である。

\begin{eqnarray}
(G \circ \alpha) (X) &=& Id (F’ (X)) \circ (G \circ \alpha (X)) \\
&=& G \circ \alpha (X)
\end{eqnarray}
となる。
次回は、随伴関手についての比喩を説明しよう。