接着関数－路線網

１．接着関数

部品を結合して製品にしたり、サブルーチンを集めてプログラムを作成したり、課をまとめて部にしたりなど、物理的な結合や概念的な結合は日常茶飯事に発生する。このような結合は、数学的には、接着関数として次のように定義される。

接着空間：ある空間\(Y\)の部分空間\(Y_0\)を別の空間\(X\)に関数\(f: Y_0 \rightarrow X\)で接着したときの空間は、
\(X \sqcup Y/ \sim = Y \sqcup_f X / (y \sim f(y) | \forall y \in Y_0 )\)
と表す。ここで、空間\(X \sqcup Y/ \sim \)は、\(y\)と\(f(y)\)とを同値と見なした商空間である。
商空間は聞きなれない専門用語かもしれない。しかし、これは日常的に使っている概念で、例えば、2進数は、偶数の数はそれぞれ同値と見なし、奇数の数はそれぞれ同値と見なした空間である。

２．路線網

地下鉄、私鉄などで構成される路線網を考えることとする。ここでは、簡単のために都内の路線網は、半蔵門線、有楽町線、大江戸線だけとする。さらに、実用的なものにするためには、この三路線からなる路線網を拡張すればよい。この拡張は理解を深める演習として丁度よいので、この記事の内容を読んだ後、挑戦するとよい。

路線網をレコードを用いて表すこととする。フィールドは、路線網を表すnames、路線網で乗換駅を表すattached、路線網には含まれないが他の路線への乗換駅となっているtransfer、路線に含まれる駅を表すstationsを用意することとする。

路線、駅、乗換駅をニーモニックを用いてLine,Station,Transferで表し、路線網をデータ型Networkでレコード構文を用いて定義する。Networkのレコード構文で、フィールドnamesは、一つの路線、あるいは、複数の路線のリストである。transfersはこの路線網以外の路線への乗換駅のリストである。attachedはこの路線網内での乗換駅のリストである。stationsはこの路線内の駅のリストである。

type Line     = String
type Station  = (Char, Int)
type Transfer = ((Line, Station),(Line, Station))
data Network  = Network {names :: [Line], transfers :: [Transfer], attached :: [Transfer], stations :: [Station]} deriving Show

半蔵門線だけで構成される路線網は以下のようになる。ここでは、有楽町線あるいは大江戸線への乗換駅がtransfersに列挙されている。また、この路線網内での乗換駅は存在しないため、空である。また、半蔵門線内の駅は、Zを先頭の文字にして渋谷駅から押上駅の方に番号が降られているので、それに似せて表現した。

hanzomon  = Network {names = ["hanzomon"], transfers = [(("hanzomon",('Z', 4)),("yurakucho",('Y', 16))),(("hanzomon",('Z', 11)),("oedo",('E', 14))),(("hanzomon",('Z', 3)),("oedo",('E', 24)))], attached = [], stations = [('Z', x) | x <- [1..14]]}

同様に有楽町線は次の通りとなる。

yurakucho = Network {names = ["yurakucho"], transfers = [(("yurakucho",('Y', 16)),("hanzomon",('Z', 4))),(("yurakucho",('Y', 21)),("oedo",('E', 16)))], attached = [], stations = [('Y', x) | x <- [1..24]]}

また、大江戸線は次のようになる。

oedo  = Network {names = ["oedo"], transfers = [(("oedo",('E', 16)),("yurakucho",('Y', 21))),(("oedo",('E', 14)),("hanzomon",('Z', 11))),(("oedo",('E', 24)),("hanzomon",('Z', 3)))], attached = [], stations = [('E', x) | x <- [1..40]]}

次に二つの路線網を乗換駅で結合して、一つの路線網にすることを考える。これは、先ほど説明した接着関数である。関数attachingは次のようになる。

attaching :: Network -> Network -> Network
attaching x y = Network {names = n, transfers = t, attached = a, stations = s}
  where 
    n  = (names x) ++ (names y)
    a1 = [ x1 | x1 <- transfers x, y1 <- transfers y, fst x1 == snd y1 &&  snd x1 == fst y1]
    a  = a1 ++ (attached x) ++ (attached y)
    t1 = [ x1 | x1 <- transfers x, and $ map (\y1 ->  x1 /= y1) a1]
    t2 = [ x1 | x1 <- transfers y, and $ map (\y1 ->  fst x1 /= snd y1 ||  snd x1 /= fst y1) a1]
    t  = t1 ++ t2
    s  = (stations x) ++ (stations y) 

この関数では、二つの路線網の乗換駅がattachedに含まれ、また、transfersからは除外されたリストが作られる。

実行結果を示すと次のようになる。

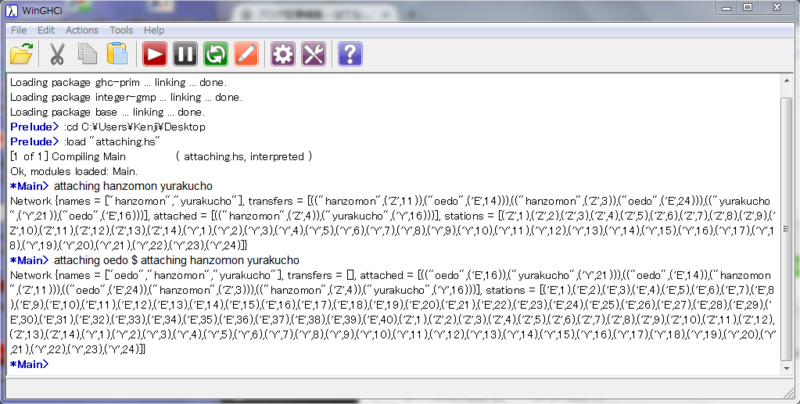
最初は、半蔵門線と有楽町線で構成される路線網、次が三つの線で構成される路線網である。それぞれ、transfersとattachedを見ると、路線外への乗換駅と路線内への乗換駅が正しいことが分かる。