1.型付きラムダ計算
バークレイの修士課程の学生だったころに、後にチューリング賞をとることになるM. Blum教授から"Theory Of Algorithms"の講義を受けた。日本の講義と比較すると、バークレイの先生たちの多くは、系統だってわかりやすく説明してくれるので、講義を楽しむことができた(もちろん、日本にも講義の上手な先生は何人かいました)。しかし、この授業だけはチャーチのラムダ計算を説明してくれた部分が難解で、教科書を何回も何回も読み直し、理解するのに随分と時間を費やした。その時の努力のおかげで、ラムダ計算に抵抗を感じることがなくなり、その後で、LispやSchemeを楽しむことができた。さらにめぐって、Haskellを好むようになるとは、講義を受けているときは想像もしなかった。
今回の記事は、型付きラムダ計算とデカルト閉圏に関する最近の研究内容である。といっても、筆者のものではなく、Conal Elliotの論理回路の合成に関する研究である。Elliotは関数型リアクティブ・プログラミング(Functional Reactive Programming:FRP)の概念に基づいて、Franというアニメーションを開発した。Franは、その後、エール大学のグループによってYampaへと引き継がれていく。彼は、関数型リアクティブ・プログラミングの世界では、先駆的な研究者である。
Elliotが最近まで取り組んでいた研究がプログラマブル・ハードウェア・アーキテクチャーである。2011年にベイエリアでのHaskellのコミュニティーで、ベンチャー企業Tabulaの創始者Taigに出会ったのが発端である。その会合の中で、verilogやVHDLに代わるハードウェア記述言語を関数型言語で、しかも、超並列で実現したいというTeigの熱望を聞き、意気投合して、研究が始まった。
筆者も、かって、大型システムのハードウェア設計に携わった経験があるので、この話題は、とても興味ある話なので、デカルト閉圏の応用と関連づけて記事にした。
2.セマンティックス
設計者は、それぞれの分野に合わせて、それに適したプログラミング言語やハードウェア記述言語を用いるが、Elliotの動機もそこにある。あるシステムをモデル化しようとするときは、それに適した記述法を用いる方がよいし、そのシステムが具体化された姿を観察するときは、それに適した記述法にするのがよい。そこで、モデル化するときの記述法と、具体的になった時の記述法を異なるものとするのだが、その時、両方の記述は、数学的に、等価でないと困る。それは、一方で正しいことが証明されれば、他方でも正しいことが保証されるためである。
Elliotがハードウェア・アーキテクチャの開発方法でとった方法は次のようになっている。論理回路の仕様は型付きラムダ計算、即ち、Haskellで記述し、論理回路や順序回路の構成はデカルト閉圏で記述する。仕様は、ハードウェアの開発者が担当するので、システムの機能を忠実に記述できる手段として、型付きラムダ計算を選択した。また、回路の構成は、CAD用のシステムが理解できればよいので、デカルト閉圏を用いた。
説明するにあたって、いくつかの例を用いて、Elliotが狙っていることが分かるようにする。
最初の例は、論理回路の合成である。この論理回路は、4つの積の合計を求めるものである。設計者はHaskell(型付きラムダ計算)を用いて、この論理回路の仕様(機能)を記述する。それは次のようになる。
sumSqure :: RTree2 Int -> Int sumSqure = sum . fmap squre
次に、これをコンパイルすると、デカルト閉圏での記述に変換される。これは、かなり見にくいのだが、次のようになる。
uncurry (apply . (curry (apply . (curry (apply . (curry (apply . (curry (curry (apply . (curry (apply . (apply . (curry (curry (uncurry add) . exr) . it &&& apply . (curry (repr . exr) . it &&& apply . (((((id . exr) . exl) . exl) . exl) . id *** (id . exl) . id))) &&& apply . (curry (repr . exr) . it &&& apply . (((((id . exr) . exl) . exl) . exl) . id *** (id . exr) . id)))) &&& apply . (curry (repr . exr) . it &&& apply . (curry (apply . (curry (abst . exr) . it &&& apply . (apply . (curry (curry id . exr) . it &&& apply . (((id . exr) . exl) . id *** (id . exl) . id)) &&& apply . (((id . exr) . exl) . id *** (id . exr) . id)))) &&& apply . (curry (repr . exr) . it &&& apply . (curry (repr . exr) . it &&& id . exr))))))) &&& curry (apply . (curry (abst . exr) . it &&& apply . (curry (apply . (curry (abst . exr) . it &&& apply . (apply . (curry (curry id . exr) . it &&& apply . (((id . exr) . exl) . id *** (id . exl) . id)) &&& apply . (((id . exr) . exl) . id *** (id . exr) . id)))) &&& apply . (curry (repr . exr) . it &&& apply . (curry (repr . exr) . it &&& id . exr))))))) &&& curry (apply . (curry (apply . (curry (abst . exr) . it &&& apply . (apply . (curry (curry (uncurry mul) . exr) . it &&& id . exr) &&& id . exr))) &&& apply . (curry (repr . exr) . it &&& id . exr))))) &&& curry (apply . (curry (apply . (curry (abst . exr) . it &&& apply . (apply . (curry (curry (uncurry add) . exr) . it &&& apply . (curry (repr . exr) . it &&& apply . (((id . exr) . exl) . id *** (id . exl) . id))) &&& apply . (curry (repr . exr) . it &&& apply . (((id . exr) . exl) . id *** (id . exr) . id))))) &&& apply . (curry (repr . exr) . it &&& apply . (curry (repr . exr) . it &&& id . exr)))))) &&& curry (apply . (curry (abst . exr) . it &&& apply . (curry (repr . exr) . it &&& id . exr))))) . (it &&& id)
上記を回路構成での記述に焼直すと次の結果が得られる。
module sumSquare-t2 (In_0, In_1, In_2, In_3, Out); input [0:31] In_0; input [0:31] In_1; input [0:31] In_2; input [0:31] In_3; output [0:31] Out; wire [0:31] w_mul_I1; wire [0:31] w_mul_I2; wire [0:31] w_mul_I3; wire [0:31] w_mul_I4; wire [0:31] w_add_I5; wire [0:31] w_add_I6; wire [0:31] w_add_I7; assign w_mul_I1 = In_0 * In_0; assign w_mul_I2 = In_1 * In_1; assign w_mul_I3 = In_2 * In_2; assign w_mul_I4 = In_3 * In_3; assign w_add_I5 = w_mul_I1 + w_mul_I2; assign w_add_I6 = w_mul_I3 + w_mul_I4; assign w_add_I7 = w_add_I5 + w_add_I6; assign Out = w_add_I7; endmodule
さらに回路図で表すと、次のようになる。
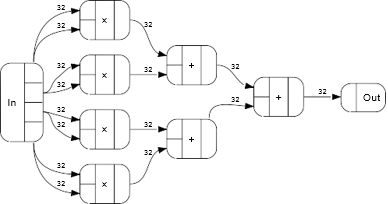
次は順序回路の合成である。ここでは、フィボナッチ数列を利用する。
フィボナッチ数列をHaskellで記述すると次のように幾通りにも表現できる。これらの表現はすべて等価である。
fib :: Num a -> Mealy ( ) a fib = Mealy ((\( ), (a,b)) -> (a, (b, a + b))) (0,1) fib = loop (arr (\ (), (a,b)) -> (a, (b, a + b))) . (0,1) fib = proc ( ) -> do rec (a, b) <- delay (0,1) -< (b, a + b) fib = proc ( ) -> do rec a <- delay 0 -< b b <- delay 1 -< a + b returnA -< a
一番最後の式を説明する。フィボナッチ数列は、\(f_{n+2} = f_{n+1} + f_n\)で定義される。この計算を行っているのが、recの部分である。a <- delay 0 -< bの部分は、\(f_n\)に関するもので、初期値は0となっている。b <- delay 1 -< a + bの部分は、\(f_{n+1}\)に関するもので、初期値は1となっている。
時間\(t\)での\(f_n\)と\(f_{n+1}\)からの出力はa,bである。また、\(f_n\)と\(f_{n+1}\)への入力はb,a+bである。これらは、時間\(t+delay\)での\(f_n\)と\(f_{n+1}\)からの出力となる。フィボナッチ数列に対応させるならば、一つずつ繰り上がるので、\(f_{n+1}\)と\(f_{n+2}\)の値b,a+bとなる。
また、retunrAの値が現時点\(t\)でのフィボナッチ数\(f_n\)を出力している。
このコードをコンパイルし、回路図に落とすと次のものが得られる。

3.Elliotの発想
彼はデカルト閉圏での語彙をハードウェアの記述と次のように結びつけた。まず、デカルト閉圏を構成している語彙に対して、圏は「射」、デカルトは「積\(\times\)」、閉は「指数対象」とした。
射は、圏論での定義の通り、ドメインとコドメインを有している。また、恒等射\(id\)と呼ばれるものが存在するとともに、射は合成\(\circ\)できる。論理回路の設計の中で、射は部品としての論理回路として、あるいは、部品を組み合わせて作成した論理回路として考えることができる。恒等射を意識することは少ないが、合成は、複数の論理回路を接続して大きな論理回路を作成するときに、当たり前のこととして用いる。
積\(\times\)は論理回路を接続するときの具体的な方法を示しているとみることができる。積のもともとの意味は、二つの対象を対として構成されている一つの対象にまとめられることを意味する。
指数対象は、射を対象として扱うことを言っている。これにより、積のところで対象についてのまとめ方を言っていたが、これは、射についてもいうことができるようになる。そこで、合成が論理回路を縦方向に接続して一つの論理回路に合成することを意味していたのに対して、積は論理回路を横方向に組み合わせて論理回路を合成できることを意味する。これにより、論理回路が縦方向、横方向に合成できるようになる。
デカルト閉圏を表すために用意したクラスは次のようなものである。
最初に圏は次のようにする。
class Category () where id :: a
a (
) :: (b
c) -> (a
b) -> (a
c)
なお、型クラスCategoryでは次の定理を満たす必要がある。
idf = f g
id = f (h
g)
f = f
(g
f)
次に積は次のようになる。
class Category () => ProductCat (
) where type a
b exl :: (a
b)
a exr :: (a
b)
b (
) :: (a
c) -> (a
d) -> (a
(c
d)) (
) :: (a
c) -> (b
d) -> ((a
b)
(c
d)) f
g = (f
exr)
(g
exr)
なお、型クラスProductCatでは次の定理を満たす必要がある。
exl(f
g) = f exr
(f
g) = g exl
h
exr
h=h exl
exr = id (f
g)
(h
k) = (f
h)
(g
k) id
id = id (f
g)
(h
k) = (f
h)
(g
k) (f
g)
h = (f
h)
(g
h)
積の可換図式は次のようになっていた。

そこで、型クラスProCategoryと積の可換図式の対応をとると次のようになる。
| 型クラス | 可換図式 |
|---|---|
| exl | \(p_1\) |
| exr | \(p_2\) |
| \(\bigtriangleup \) | \(u = < f_1, f_2 > \) |
また、型クラスの\(\times\)は下の可換図式に対応している。

次に閉は次のようになる。
class Category () => ClosedCat (
) where type a
b apply :: ((a
b)
a)
b curry :: ((a
b)
c) -> (a
(b
c)) uncurry :: (a
(b
c)) -> ((a
b)
c)
なお、デカルト閉圏の可換図式は次のようになっていた。

そこで、型クラスClosedCatとデカルト閉圏の可換図式の対応をとると次のようになる。
| 型クラス | 可換図式 |
|---|---|
| apply | \(\epsilon\) |
| curry | \(\tilde{f}\) |
| uncurry | \(f=\epsilon \circ (\tilde{f} \times 1_A) \) |
積は二つの論理回路を横方向につないで一つの論理回路を同棲すると前に説明したが、そのつなぎ方は、可換図式から連想すると、\(A \times B\)から矢印が出ているので、フォークと考えることができる。これに対して、方向が逆であるジョインも考えることができるので、Elliotは余積も次のように含めた。
class Category () => CoproductCat (
) where type a
b inl :: a
(a
b) inr :: b
(a
b) (
) :: (a
c) -> (b
c) -> ((a
b)
c) (
) :: (a
c) -> (b
d) -> ((a
b)
(c
d)) f
g = (inl
f)
(inr
g)
なお、型クラスCoproductCatでは次の定理を満たす必要がある。
(fg)
inl = f (f
g)
inr = g h
inl
h
inr = h inl
inr=id (h
k)
(f
g) = (h
f)
(k
g) id
id=id (h
k)
(f
g) = (h
f)
(k
g) h
(f
g) = (h
f)
(h
g)
余積の可換図式は次のようになる。

そこで、型クラスProCategoryと積の可換図式の対応をとると次のようになる。
| 型クラス | 可換図式 |
|---|---|
| inl | \(q_1\) |
| inr | \(q_2\) |
| \(\bigtriangledown \) | \(u' = [ g_1, g_2 ] \) |
また、型クラスの\(+\)は下の可換図式に対応している。
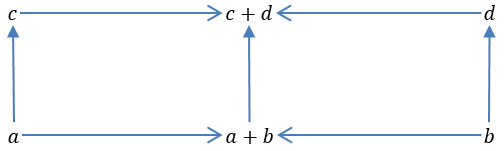
最後に、型付きラムダ計算からデカルト閉圏への変換は、大まかにいうと、次の式をHaskellで実装することになるが、詳細を知りたい場合には、Elliotの資料を参考にしてほしい。
\begin{eqnarray}
(\lambda p \rightarrow k) & ---> & con st \ k \\
(\lambda p \rightarrow u \ v) & ---> & apply \circ ( (\lambda p \rightarrow u) \bigtriangleup (\lambda p \rightarrow v))\\
(\lambda p \rightarrow \lambda q \rightarrow u) & ---> & curry ( \lambda (p,q) \rightarrow u)
\end{eqnarray}