昨日は退職者慰労会が催された。これで、本当に退職するのだなあという実感がわいてきた。家に戻って、退職後の仕事をする場所の整備に取り掛かった。主たる仕事は、文章を書いたり、プログラムを作成したりなので、まず最初にパソコン関係の設置を行った。座った時に、南面の窓が左側になるようにして、写真のように、西側の壁に沿って、ディスプレイを置いた。
左側の二つのディスプレイはWindows用。主に、文章作成に利用する。右側のディスプレイはUbuntu用。主に、プログラムの作成用だ。
その他に手元に置いておくのは、AmazonのKindle Foreだ。7,8.9,10インチのものを持っているが、一番小さい7インチのものを一番よく用いている。軽いのが何よりだと思う。Kindleには、既に500冊以上もの書籍が収納されているので、大変に重宝している。大学を辞めると家の中が本であふれ、床が抜けたという話を聞くこともあるが、大学にあった千冊近くの本は、貴重な本もあったが、すべて大学に還元した。
4.イベントを理解する
前回の記事で、イベントを次のように定義した。
-- | Event is modeled by an /infinite/ list of 'Maybe' values. -- It is isomorphic to @Time -> Maybe a@. -- -- 'Nothing' indicates that no occurrence happens, -- while 'Just' indicates that an occurrence happens. newtype Event a = E { unE :: [Maybe a] } deriving (Show)
この定義は分かりにくかったかもしれない。分からなくなったときは、基本に立ち戻って考えるのがよい。圏論の用語を用いて説明すると次のようになる。
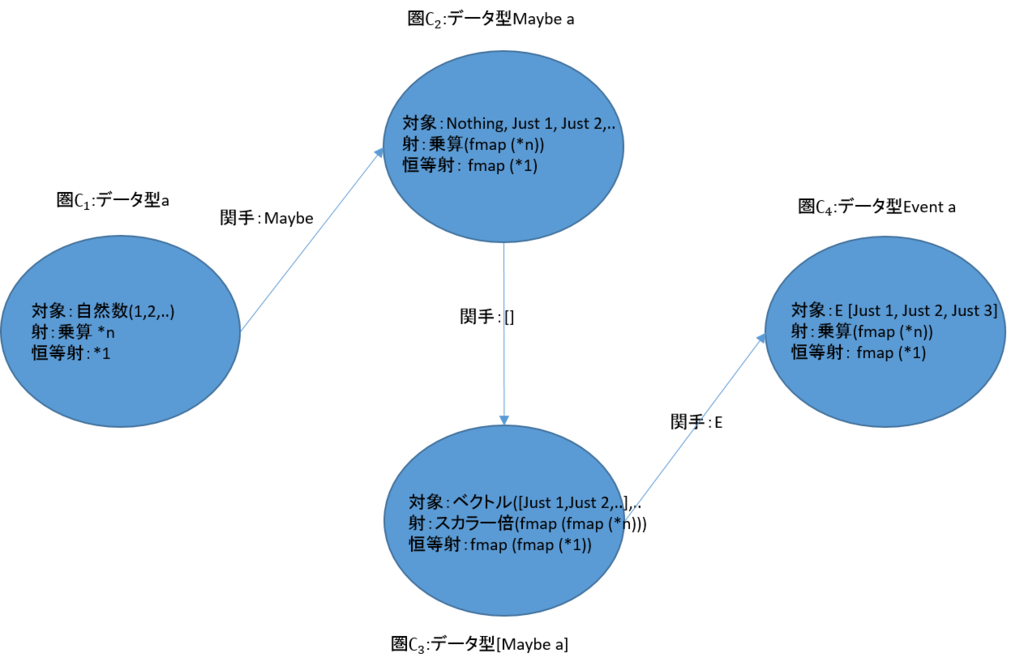
簡単な圏として、1以上の自然数の乗算を扱う圏\(\mathcal C_1\)を考えよう。圏の定義の仕方は一意的ではなく、幾通りもの方法が考えられる(しかし、それらはお互いに同値である)。ここでは、対象を1から始まる自然数とする。また、射を\(*n\)としよう。\(n\)はやはり1から始まる自然数である。この時、恒等射は1である。ドメインとコドメインは1から始まる自然数である。射の合成は\(*m \circ *n = *(m \times n)\)と定義する。この圏\(\mathcal C_1\)を下図の左側に示した。
イベントは、Maybeとリスト[ ]を用いて定義されているので、次に、この二つの圏を定義しよう。これらは、上図の真ん中の二つの図で示した。
Maybeの\(\mathcal C_2\)では、対象を\(Nothing\)と\(Just \ n\) (但し\(n\)は1以上の自然数)とした。また、Maybeを、圏\(\mathcal C_1\)からの関手で対応づけているので、射は\(fmap \ (*n)\)となる。恒等射は、もちろん、\(fmap \ (*1)\)となる。射を確認しよう。
*Reactive.Banana.Model> let a = Just 4 *Reactive.Banana.Model> fmap (*3) a Just 12
リストの\(\mathcal C_3\)では、対象を、要素が1以上の自然数であるベクトルとした。また、リストを、圏\(\mathcal C_1\)からの関手で対応づけているので、射は、この場合はスカラー倍となるが、\(fmap \ (*n)\)となる。恒等射は、もちろん、\(fmap \ (*1)\)となる。同じように、射を確認しよう。
*Reactive.Banana.Model> let b = [3, 2, 5] *Reactive.Banana.Model> fmap (*3) b [9,6,15]
イベントは、Maybeの圏\(\mathcal C_2\)を関手[]で対応付けたようなもの、あるいは、リストの\(\mathcal C_4\)を関手maybeで対応付けたようなものに近い。イベントをMaybeとリストと同じように、圏\(\mathcal C_1\)からの関手Eventで対応づけているものとすると、この圏\(\mathcal C_4\)は、対象をMaybeの対象をリストにしたものとなる(但し、リストの前に値コンストラクタのEが付く)。また、射は、上の二つと同様で、\(fmap \ (*n)\)となる。恒等射は、もちろん、\(fmap \ (*1)\)となる。ここでも、射を確認しよう。
*Reactive.Banana.Model> let c = [Just 3, Just 2, Nothing] *Reactive.Banana.Model> let d = E c *Reactive.Banana.Model> fmap (*3) d E {unE = [Just 9,Just 6,Nothing]}
正しく、働いていることが分かった。
なお、Reactive.Banana.Modelでは、Eventのファンクタは次のように定義されている。
instance Functor Event where fmap f (E xs) = E (fmap (fmap f) xs)
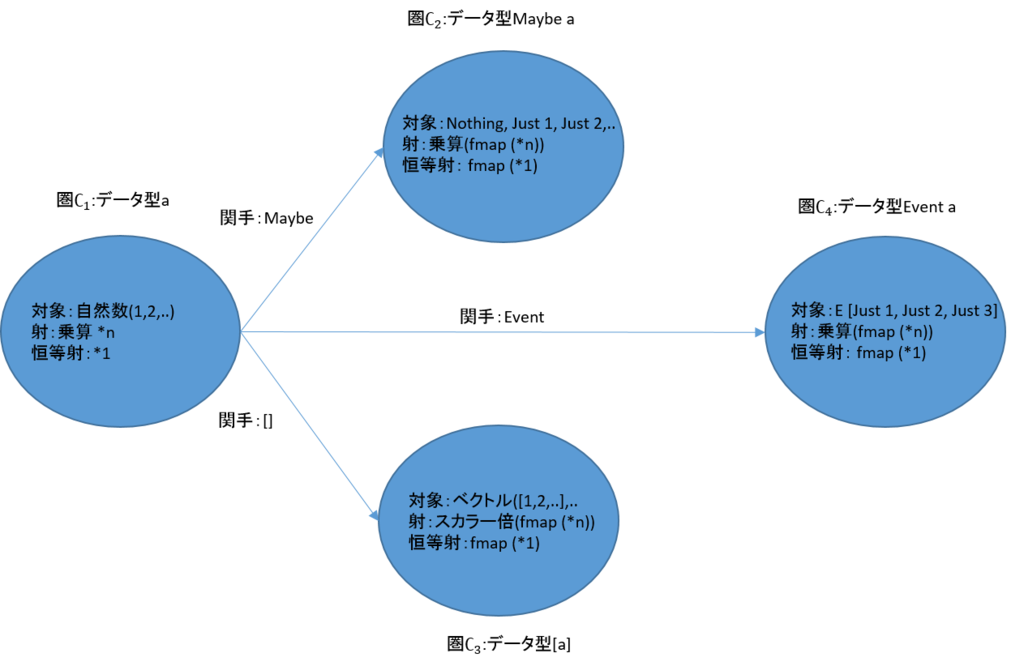
右側の式は、Maybeの値を要素とするリストxsを作成し、その要素のそれぞれに、即ちMaybeの値に、\(fmap \ f\)を施してやり、それをリストとして返すというものである。圏\(\mathcal C_2\)を関手[ ]で対応づけた圏\(\mathcal C_3\)を作成し、それを関手Eventで対応づけた圏\(\mathcal C_4\)を得よといっている。これを確認すると次のようになる。
*Reactive.Banana.Model> let c = [Just 3, Just 2, Nothing] *Reactive.Banana.Model> let e = fmap (fmap (*3)) c *Reactive.Banana.Model> e [Just 9,Just 6,Nothing] *Reactive.Banana.Model> E e E {unE = [Just 9,Just 6,Nothing]}
また、これを図で示すと次のようになる。