Reactive Bananaで学ぶリアクティブ・プログラミング（３）

５．音符をイベントに

最近は楽譜を作成するソフトには素晴らしいものがいくつかあり、わざわざ、Reactive Bananaを用いて楽譜を表そうとしても意味がないのかもしれない。しかし、現実の世界を関数型言語でどのように表すことができるのかを提示することは、他の分野に応用していくときに参考になると思う。

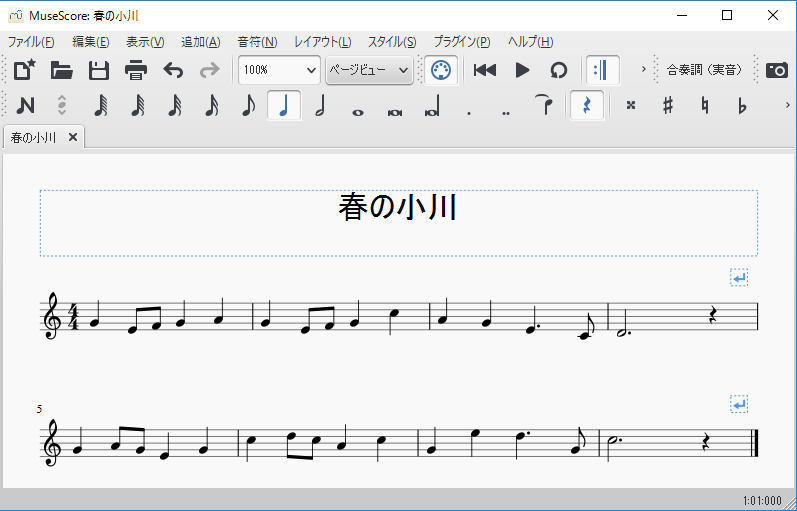
MuseScorを用いて、春の小川の楽譜を書いてみた。

５．１　音階をデータ型に

楽譜をHaskellで表せるようにするためには、音階を表す手段を考えなければならない。音階にはいろいろな表し方がある。ドイツ語表記のC,D,E..を用いることが多いが、ここでは、小学校以来使っているイタリア語表記のDo,Re,Mi..を用いることとする。また、音階は、オクターブ違っても同じ記号が使われるが、ここでは、一オクターブ高い音階には、音階を示す記号の後に5をつけることとする。例えば、1オクターブ高いドであれば、Do5とする。また、ここでは、シャープやフラットのような半音上げたり下げたりすることはないものとする。このような制限をして、音階を示すデータ型scaleを次のように定義する。

data Scale = Do | Re | Mi | Fa | So | La | Si | Do5 | Re5 | Mi5 | Fa5 | So5 | La5 | Si5 | Rest deriving (Show, Read, Eq, Ord)

なお、上記の定義でRestは休符である。

５．２　各小節を表す

小節は次のように表すこととする。時間の単位は8分音符を1単位とする。これにより、4分音符は2単位を使用する。そこで、最初の1単位で音を出し、次の1単位では継続することにする。他の音符についても同様に考える。

各小節の音は、音階をMaybeに移し、その列で表すこととする。春の小川の第一小節は、4分音符のソ、8分音符のミ、8分音符のファ、4分音符のソ、4分音符のラで構成されている。そこで、最初の4分音符のソは最初の1単位でソの音を出すので、これはJust Soとなる。次の1単位は継続なので、これはNothingで表すことにする。この結果、最初の4分音符は[Just So, Nothing]で表すこととする。次の8分音符のミは[Just Mi]となる。

これを続けると第一小節は、次のようになる。

score1 = [ Just So,  Nothing, Just Mi,  Just Fa,  Just So,  Nothing, Just La,   Nothing] 

春の小川のスコア―を表すと、次のようになる。

score1 = [ Just So,  Nothing, Just Mi,  Just Fa,  Just So,  Nothing, Just La,   Nothing]  

score2 = [ Just So,  Nothing, Just Mi,  Just Fa,  Just So,  Nothing, Just Do5,  Nothing]  

score3 = [ Just La,  Nothing, Just So,  Nothing,  Just Mi,  Nothing, Nothing,   Just Do]  

score4 = [ Just Re,  Nothing, Nothing,  Nothing,  Nothing,  Nothing, Just Rest, Nothing]  

score5 = [ Just So,  Nothing, Just La,  Just So,  Just Mi,  Nothing, Just So,   Nothing]  

score6 = [ Just Do5, Nothing, Just Re5, Just Do5, Just La,  Nothing, Just Do5,  Nothing]  

score7 = [ Just So,  Nothing, Just Mi5, Nothing,  Just Re5, Nothing, Nothing,   Just So]  

score8 = [ Just Do5, Nothing, Nothing,  Nothing,  Nothing,  Nothing, Just Rest, Nothing]

５．３　打鍵をイベントに

春の小川のスコア―を得たので、これをピアノを弾くときの打鍵という動作に変えてみる。これは、Eventに移してあげればよいので次のようになる。

play = E $ score1 ++ score2 ++ score3 ++ score4 ++ score5 ++ score6 ++ score7 ++ score8

playというイベントは当然のことだが次のようになっている。

Prelude> :load "Music.hs"
[1 of 2] Compiling Model            ( Model.hs, interpreted )
[2 of 2] Compiling Main             ( Music.hs, interpreted )
Ok, modules loaded: Model, Main.
*Main> unE play
[Just So,Nothing,Just Mi,Just Fa,Just So,Nothing,Just La,Nothing,Just So,Nothing,Just Mi,Just Fa,Just So,Nothing,Just Do5,Nothing,Just La,Nothing,Just So,Nothing,Just Mi,Nothing,Nothing,Just Do,Just Re,Nothing,Nothing,Nothing,Nothing,Nothing,Just Rest,Nothing,Just So,Nothing,Just La,Just So,Just Mi,Nothing,Just So,Nothing,Just Do5,Nothing,Just Re5,Just Do5,Just La,Nothing,Just Do5,Nothing,Just So,Nothing,Just Mi5,Nothing,Just Re5,Nothing,Nothing,Just So,Just Do5,Nothing,Nothing,Nothing,Nothing,Nothing,Just Rest,Nothing]

５．４　プログラムの全体

ここまでに用いたプログラムを示す。

import Model

data Scale = Do | Re | Mi | Fa | So | La | Si | Do5 | Re5 | Mi5 | Fa5 | So5 | La5 | Si5 | Rest deriving (Show, Read, Eq, Ord)


score1 = [ Just So,  Nothing, Just Mi,  Just Fa,  Just So,  Nothing, Just La,   Nothing]  

score2 = [ Just So,  Nothing, Just Mi,  Just Fa,  Just So,  Nothing, Just Do5,  Nothing]  

score3 = [ Just La,  Nothing, Just So,  Nothing,  Just Mi,  Nothing, Nothing,   Just Do]  

score4 = [ Just Re,  Nothing, Nothing,  Nothing,  Nothing,  Nothing, Just Rest, Nothing]  

score5 = [ Just So,  Nothing, Just La,  Just So,  Just Mi,  Nothing, Just So,   Nothing]  

score6 = [ Just Do5, Nothing, Just Re5, Just Do5, Just La,  Nothing, Just Do5,  Nothing]  

score7 = [ Just So,  Nothing, Just Mi5, Nothing,  Just Re5, Nothing, Nothing,   Just So]  

score8 = [ Just Do5, Nothing, Nothing,  Nothing,  Nothing,  Nothing, Just Rest, Nothing]

play = E $ score1 ++ score2 ++ score3 ++ score4 ++ score5 ++ score6 ++ score7 ++ score8

また、MedelはReactive.Banana.Modelと同一のモジュールだが、このモジュールをimportするとうまく動かないので、同一ディレクトリー内にモジュール名をModelにして呼び出せるようにした。その内容は次の通りである。

{-----------------------------------------------------------------------------
    reactive-banana
------------------------------------------------------------------------------}
{-# LANGUAGE RecursiveDo #-}
module Model (
    -- * Synopsis
    -- | Model implementation for learning and testing.

    -- * Overview
    -- $overview

    -- * Core Combinators
    -- ** Event and Behavior
    Nat, Time,
    Event(..), Behavior(..),
    interpret,
    -- ** First-order
    module Control.Applicative,
    never, unionWith, filterJust, apply,
    -- ** Moment and accumulation
    Moment(..), accumE, stepper,
    -- ** Higher-order
    valueB, observeE, switchE, switchB,
    ) where

import Control.Applicative
import Control.Monad
import Control.Monad.Fix

{-$overview

This module reimplements the key FRP types and functions from the module
"Reactive.Banana.Combinators" in a way that is hopefully easier to understand.
Thereby, this model also specifies the semantics of the library.
Of course, the real implementation is much more efficient than this model here.

To understand the model in detail, look at the source code!
(If there is no link to the source code at every type signature,
then you have to run cabal with --hyperlink-source flag.)

This model is /authoritative/:
Event functions that have been constructed using the same combinators
/must/ give the same results when run with the @interpret@ function
from either the module "Reactive.Banana.Combinators"
or the module "Reactive.Banana.Model".
This must also hold for recursive and partial definitions
(at least in spirit, I'm not going to split hairs over @_|_@ vs @\\_ -> _|_@).

-}

{-----------------------------------------------------------------------------
    Event and Behavior
------------------------------------------------------------------------------}
-- | Natural numbers (poorly represented).
type Nat = Int

-- | The FRP model used in this library is actually a model with continuous time.
--
-- However, it can be shown that this model is observationally
-- equivalent to a particular model with (seemingly) discrete time steps,
-- which is implemented here.
-- The main reason for doing this is to be able to handle recursion correctly.
-- Details will be explained elsewhere.
type Time = Nat -- begins at t = 0

-- | Event is modeled by an /infinite/ list of 'Maybe' values.
-- It is isomorphic to @Time -> Maybe a@.
--
-- 'Nothing' indicates that no occurrence happens,
-- while 'Just' indicates that an occurrence happens.
newtype Event a = E { unE :: [Maybe a] } deriving (Show)

-- | Behavior is modeled by an /infinite/ list of values.
-- It is isomorphic to @Time -> a@.
newtype Behavior a = B { unB :: [a] } deriving (Show)

interpret :: (Event a -> Moment (Event b)) -> [Maybe a] -> [Maybe b]
interpret f as =
    take (length as) . unE . (\m -> unM m 0) . f . E $ (as ++ repeat Nothing)

{-----------------------------------------------------------------------------
    First-order
------------------------------------------------------------------------------}
instance Functor Event where
    fmap f (E xs) = E (fmap (fmap f) xs)

instance Functor Behavior where
    fmap f (B xs) = B (fmap f xs)

instance Applicative Behavior where
    pure x          = B $ repeat x
    (B f) <*> (B x) = B $ zipWith ($) f x

never :: Event a
never = E $ repeat Nothing

unionWith :: (a -> a -> a) -> Event a -> Event a -> Event a
unionWith f (E xs) (E ys) = E $ zipWith combine xs ys
    where
    combine (Just x) (Just y) = Just $ f x y
    combine (Just x) Nothing  = Just x
    combine Nothing  (Just y) = Just y
    combine Nothing  Nothing  = Nothing

filterJust :: Event (Maybe a) -> Event a
filterJust = E . fmap join . unE

apply :: Behavior (a -> b) -> Event a -> Event b
apply (B fs) = E . zipWith (\f mx -> fmap f mx) fs . unE

{-----------------------------------------------------------------------------
    Moment and accumulation
------------------------------------------------------------------------------}
newtype Moment a = M { unM :: Time -> a }

instance Functor     Moment where fmap f = M . fmap f . unM
instance Applicative Moment where
    pure   = M . const
    (<*>)  = ap
instance Monad Moment where
    return = pure
    (M m) >>= k = M $ \time -> unM (k $ m time) time

instance MonadFix Moment where
    mfix f = M $ mfix (unM . f)

-- Forget all event occurences before a particular time
forgetE :: Time -> Event a -> [Maybe a]
forgetE time (E xs) = drop time xs

stepper :: a -> Event a -> Moment (Behavior a)
stepper i e = M $ \time -> B $ replicate time i ++ step i (forgetE time e)
    where
    step i ~(x:xs) = i : step next xs
        where next = case x of
                        Just i  -> i
                        Nothing -> i

-- Expressed using recursion and the other primitives
-- FIXME: Strictness!
accumE :: a -> Event (a -> a) -> Moment (Event a)
accumE a e1 = mdo
    let e2 = ((\a f -> f a) <$> b) `apply` e1
    b <- stepper a e2
    return e2

{-----------------------------------------------------------------------------
    Higher-order
------------------------------------------------------------------------------}
valueB :: Behavior a -> Moment a
valueB (B b) = M $ \time -> b !! time

observeE :: Event (Moment a) -> Event a
observeE = E . zipWith (\time -> fmap (\m -> unM m time)) [0..] . unE

switchE :: Event (Event a) -> Moment (Event a)
switchE es = M $ \t -> E $
    replicate t Nothing ++ switch (unE never) (forgetE t (forgetDiagonalE es))
    where
    switch (x:xs) (Nothing : ys) = x : switch xs ys
    switch (x: _) (Just xs : ys) = x : switch (tail xs) ys

forgetDiagonalE :: Event (Event a) -> Event [Maybe a]
forgetDiagonalE = E . zipWith (\time -> fmap (forgetE time)) [0..] . unE

switchB :: Behavior a -> Event (Behavior a) -> Moment (Behavior a)
switchB b e = diagonalB <$> stepper b e

diagonalB :: Behavior (Behavior a) -> Behavior a