これまで、Haskellと結びつけながら量子力学の世界を説明してきた。そのため、Haskellに邪魔されて量子力学の世界が分かりにくくなったかもしれない。
そこで、この記事では、これまでの話をまとめながら、量子力学の世界を、離散系から連続系へと展開させてみたい。
9.離散系
ここは、量子力学の初歩をHaskellで学ぶの中の、ブラとケットおよび重ね合わせの記事の要約である。
これまで、量子力学の世界を一次元空間の離散系として見てきた。この離散系は、下図に示すように、粒子は格子点で区切られた場所に存在する。

この時、格子点間の距離を\(d\)とし、格子点を区別できるように番号\(l\)をつけて考えた。
粒子の状態は、ケットあるいはブラで表した。真空状態を\( | 0 > \)あるいは\( < 0 | \)で表した。状態からは、演算子を作用させることで新しい状態を作ることができる。演算子には、発生演算子\(\hat{a}^\dagger_l\)と消滅演算子\(\hat{a}_l\)がある。\(\hat{a}^\dagger_l\)は\(l\)番目の格子点に一つの粒子を生成し、\(\hat{a}_l\)は\(l\)番目の格子点から一つの粒子を消滅する。
\(l\)番目の格子点に粒子が一つ存在している状態は\(\hat{a}^\dagger_l | 0 > \)と表すことができる。量子力学では、一つの粒子しか存在しないのだが、それが存在する格子点の場所を特定できないという現象が存在する。しかし、観察すると粒子はどこかの格子点で見つかる。そこで、観察したときに、番号\(l\)で見つかる確率(頻度)を\(\varphi_l\)とする。そして、この現象を重ね合わせ状態\(\hat{\Psi}^\dagger | 0 > = \displaystyle \sum_l \psi_l\hat{a}^\dagger_l | 0 >\)で表す。あるいは、ブラで表現するとこの状態は\(< 0 | \hat{\Psi} = < 0 | \displaystyle \sum_l \hat{a}_l \psi^*_l \)である。なお、\(\psi_l\)と\(\psi^*_l\)は互いに共役な数である。
また、\(< 0 | \hat{\Psi} \hat{\Psi}^\dagger | 0 > = < 0 |\displaystyle \sum^\infty_{l=-\infty} \hat{a}_l \psi^*_l \psi_l \hat{a}^\dagger_l | 0 > = 1\)の時、即ち、\(\displaystyle \sum^\infty_{l=-\infty} \psi^*_l \psi_l = 1\)の時、確率\(\varphi_l\)は規格化されているという
9.1 飛び移る粒子の固有状態
ここは、有限系を説明した記事の要約である。
図のように粒子が隣の格子点に飛び移るモデルを考えてみよう。
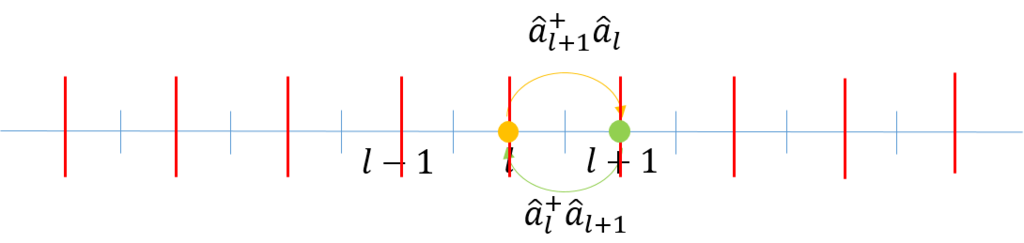
これに対するハミルトニアンは次のようになる。
\begin{eqnarray}
\hat{H}=-g \sum_l(\hat{a}^l_{l+1}\hat{a}_{l}+\hat{a}^l_{l}\hat{a}_{l+1})
\end{eqnarray}
そして、一つの粒子が重なり合っている状態\(| \Psi >= \displaystyle \sum_l\psi_l(t) \hat{a}^\dagger_l |0>\)に\(\hat{H}\)を作用させると、時間発展方程式\(i \hbar \frac{d}{dt} | \Psi(t)> = \hat{H}| \Psi(t)>\)は次のようになる。
\begin{eqnarray}
i \hbar \frac{d}{dt} \displaystyle \sum_l \psi_l(t)\hat{a}^\dagger_l |0> = -g \displaystyle \sum_l [\psi_{l-1}(t)+\psi_{l+1}(t)] \hat{a}^\dagger_l |0>
\end{eqnarray}
これから、次の微分方程式をえる。
\begin{eqnarray}
i \hbar \frac{d}{dt} \psi_m(t) = -g[ \psi_{m -1}(t)+\psi_{m +1}(t)]
\end{eqnarray}
この方程式の解は、
\begin{eqnarray}
\psi_l(t) = Ae^{-iwt}e^{i\kappa l}
\end{eqnarray}
で、\(\kappa\)は隣り合う格子点での位相差である。
また、上の解は次の分散関係を満たさなければならない。
\begin{eqnarray}
\psi_l(t) = Ae^{-iwt}e^{i\kappa l}=\phi_\omega(t) \varphi_{\kappa l}
\end{eqnarray}
ここで、
\begin{eqnarray}
\phi_\omega(t) &=& e^{-iwt} \\
\varphi_{\kappa l} &=& A e^{i\kappa l}
\end{eqnarray}
解は、時間に関係する関数\(e^{-iwt}\)と位置に関する\(e^{ikl}\)の積によって与えられる。
注意:任意の演算子\(\hat{O}\)に対して、平均値\(<\Psi(t)|\hat{O}|\Psi(t)>\)が時間\(t\)に関係しないとき、状態\(|\Psi(t)>\)を定常状態と呼ぶ。また、\(|\Psi(t)>\)が時間発展方程式の解であるとき、これを定常解という。従って、\(\psi_l(t) = Ae^{-iwt}e^{i\kappa l}\)は定常解である。
9.2 \(e^{i\kappa l}\)を係数に持つ重ね合わせ状態
\(e^{i\kappa l}\)を係数に持つ重ね合わせ状態を考えることにする。
\begin{eqnarray}
\displaystyle \sum_l \phi_{\kappa l} \hat{a}^\dagger_l |0> = \displaystyle \sum_l A e^{i\kappa l} \hat{a}^\dagger_l |0>
\end{eqnarray}
これに、飛び移る粒子に対するハミルトニアンを作用させると、
\begin{eqnarray}
\hat{H} \displaystyle \sum_l A e^{i\kappa l} \hat{a}^\dagger_l |0> = -2g \cos \kappa \displaystyle \sum_l A e^{i\kappa l} \hat{a}^\dagger_l |0> = E \displaystyle \sum_l A e^{i\kappa l} \hat{a}^\dagger_l |0>
\end{eqnarray}
但し、\(E=-2g \cos \kappa \)とする。なお、\(E\)は物理的な量としてはエネルギーである。
\(-2g \cos \kappa\)が係数なので、\(\displaystyle \sum_l A e^{ikl} \hat{a}^\dagger_l |0>\)は\(\hat{H}\)の固有状態、\(E=-2g \cos \kappa\)は\(\hat{H}\)の固有値である。
固有状態が見つかると、定常状態はこれより簡単に求めることができる。いま、固有状態を\(|\varepsilon>\)とすると、定常状態は
\begin{eqnarray}
| \Psi(t) > = e^{-i(E / \hbar)t} | \varepsilon> =e^{-iwt} | \varepsilon>
\end{eqnarray}
となる。
注意:ある状態\(|\Psi(t)>\)に演算子\(\hat{O}\)を作用させたとき、
\begin{eqnarray}
\hat{O} | \Psi(t) > = \lambda | \Psi(t) >
\end{eqnarray}
となるとき、 \(\lambda\)を固有値、\( | \Psi(t) > \)を固有状態という。なお、\(\lambda\)は係数である。
9.3 周期系
ここは、周期系を説明した記事の要約である。

周期系での飛び移る粒子のハミルトニアンは次のようになる。
\begin{eqnarray}
\hat{H}_{periodic}=-g\sum_{l=0}^{N-1} (\hat{a}^\dagger_{l+1} \hat{a}_l + \hat{a}^\dagger_{l} \hat{a}_{l+1})
\end{eqnarray}
なお、\(l=N\)の時、\(l=0\)である。
このハミルトニアン\( \hat{H}_{periodic} \)の固有状態は平面波状態
\begin{eqnarray}
\displaystyle \sum^{N-1}_{l=0} \phi_{\kappa l} \hat{a}^\dagger_l |0> = \displaystyle \sum^{N-1}_{l=0} A e^{i\kappa l} \hat{a}^\dagger_l |0>
\end{eqnarray}
である。ここで、
\begin{eqnarray}
\kappa &=& \frac{2 \pi m}{N} \\
k= \frac{2 \pi m}{Nd} &=& \frac{2 \pi m}{L}
\end{eqnarray}
なお、\(m\)は整数である。これの取りうる値については後で述べる。また、 \(\kappa\)と\(k\)は離散的な値しか取れないことに注意。
固有状態が波数で表わされているので、この状態を\(|\kappa >\)で表すこととする。即ち、
\begin{eqnarray}
|\kappa > = \displaystyle \sum^{N-1}_{l=0} \phi_{\kappa l} \hat{a}^\dagger_l |0> = \displaystyle \sum^{N-1}_{l=0} A e^{i\kappa l} \hat{a}^\dagger_l |0>
\end{eqnarray}
とする。
また、規格化して\(A\)の値を得ておこう。
\begin{eqnarray}
\displaystyle \sum^{N-1}_{l=0} P'_{l} &=& 1 \\
P'_{l}=\varphi^*_{\kappa l}\varphi_{\kappa l} &=& A^2
\end{eqnarray}
より、\(A=\frac{1}{\sqrt N}\)
となる。
これより平面波状態は次のようになる。ついでにブラの方も示しておこう。
\begin{eqnarray}
|\kappa > = \displaystyle \sum^{N-1}_{l=0} \phi_{\kappa l} \hat{a}^\dagger_l |0> &=& \displaystyle \sum^{N-1}_{l=0} \frac{1}{\sqrt N} e^{i\kappa l} \hat{a}^\dagger_l |0> \\
<\kappa | = \displaystyle \sum^{N-1}_{l=0} <0| \hat{a}_l \phi^*_{\kappa l} &=& \displaystyle \sum^{N-1}_{l=0} <0| \hat{a}_l \frac{1}{\sqrt N} e^{-i\kappa l}
\end{eqnarray}
\begin{eqnarray}
<\kappa |\kappa ' > = \delta_{kk'}
\end{eqnarray}
である。\(\delta_{kk'}\)は\(k=k'\)の時1、そうでない時0である。従って、平面波状態は直交している。
平面波状態\( |\kappa > = \displaystyle \sum^{N-1}_{l=0} \phi_{\kappa l} \hat{a}^\dagger_l |0>\)は、生成演算子\(\hat{a}^\dagger_l\)の線形結合になっている。そこで、線形結合の部分を\(a^\dagger_{[\kappa]}\)で表すと、次のようになる。
\begin{eqnarray}
\hat{a}^\dagger_{[\kappa]} = \displaystyle \sum^{N-1}_{l=0} \phi_{\kappa l} \hat{a}^\dagger_l &=& \displaystyle \sum^{N-1}_{l=0} \frac{1}{\sqrt N} e^{i\kappa l} \hat{a}^\dagger_l \\
\hat{a}_{[\kappa]} = \displaystyle \sum^{N-1}_{l=0} \phi^*_{\kappa l} \hat{a}_l &=& \displaystyle \sum^{N-1}_{l=0} \frac{1}{\sqrt N} e^{-i\kappa l} \hat{a}_l
\end{eqnarray}
\(\hat{a}^\dagger_{[\kappa]}\)と\(\hat{a}_{[\kappa]}\)は波数\(k=\kappa / d\)の生成演算子、消滅演算子と考えることができる。
逆に\( \hat{a}^\dagger_{[\kappa]}\)と\(\hat{a}_{[\kappa]}\)を用いて、\( \hat{a}^\dagger_l\)と\(\hat{a}_l\)を次のように表すこともできる。
\begin{eqnarray}
\hat{a}^\dagger_l = \displaystyle \sum_\kappa \phi^*_{\kappa l} \hat{a}^\dagger_l &=& \displaystyle \sum_\kappa \frac{1}{\sqrt N} e^{-i\kappa l} \hat{a}^\dagger_{[\kappa]} \\
\hat{a}_l = \displaystyle \sum_\kappa \phi_{\kappa l} \hat{a}_l &=& \displaystyle \sum_\kappa \frac{1}{\sqrt N} e^{i\kappa l} \hat{a}_{[\kappa]}
\end{eqnarray}
なお、\(\kappa = \frac{2 \pi m}{N}\)で\(m=0,1,..,N-1\)の値をとる(他にも\(m\)の取り方はある。これは任意の\(i\)に対して\(j=m \times i + j\)なので、\(N\)個の独立な\(m\)の取り方はいかようにもなる。例えば、連続した\(m\)個の整数を取ってもよい) 。
10.連続系
10.1 周期系
今までは離散系で考えていたが、連続で考えたほうが分かりやすい場合もあるし、もっといいことには、数学的には取り扱いやすい場合も多い(逆に、情報科学の場合には面倒くさいことになる)。
波数の生成演算子\(\hat{a}^\dagger_{[\kappa]}\)を一次元の連続な空間で定義することとしよう。式の展開は大幅に省くので、詳しくは、西野友年著『場の理論』を参考にして欲しい。
\(x=ld\)とすると次の関係が成り立つ。
\begin{eqnarray}
\varphi_k(x)=\varphi_{kl} / \sqrt {d} \\
\hat{a}^\dagger(x) \leftarrow \hat{a}^\dagger_l / \sqrt {d} \ \ (d \leftarrow 0) \\
\hat{a}(x) \leftarrow \hat{a}_l / \sqrt {d} \ \ (d \leftarrow 0)
\end{eqnarray}
これを利用すると、
\begin{eqnarray}
&&\hat{a}^\dagger_{[\kappa]} \\
&=& \sum^{N-1}_{l=0} \varphi_{kl}\hat{a}^\dagger_{l} \\
&=& d \sum^{N-1}_{l=0} \frac{\varphi_{kl}}{\sqrt {d}} \frac{\hat{a}^\dagger_{l}}{\sqrt {d}} \\
&\rightarrow& d \sum^{N-1}_{l=0} \varphi_k (ld) \hat{a}^\dagger(ld) \ \ (d \leftarrow 0) \\
&=& \int^L_{x=0} \varphi_k (x) \hat{a}^\dagger(x) dx \\
&=& \int^L_{x=0} \frac{e^{ikx}}{\sqrt{L}} \hat{a}^\dagger(x) dx
\end{eqnarray}
上記の最後の式は、\(\kappa\)ではなく、波数\(k\)で表わされているので、\(\hat{a}^\dagger_{[\kappa]}\)を\(\hat{a}^\dagger_k\)で表すことにすると、
\begin{eqnarray}
\hat{a}^\dagger_k = \int^L_{x=0} \frac{e^{ikx}}{\sqrt{L}} \hat{a}^\dagger(x) dx
\end{eqnarray}
同様に
\begin{eqnarray}
\hat{a}_k = \int^L_{x=0} \frac{e^{-ikx}}{\sqrt{L}} \hat{a}(x) dx
\end{eqnarray}
また、
\(\hat{a}^\dagger(x)\)と\(\hat{a}(x)\)もそれぞれ波数での発生演算子の線形結合と消滅演算子での線形結合で表すことができる。これらをまとめたのが以下の表である。
\begin{array}{|c|c|c|}
\hline
& 離散系 & 連続系 \\
\hline
位& \hat{a}^\dagger_l = \displaystyle \sum^{N-1}_{l=0} \frac{e^{-i \kappa l}}{\sqrt{N}} \hat{a}^\dagger_{[\kappa]} & \hat{a}^\dagger(x) = \displaystyle \sum_k \frac{e^{-i k x}}{\sqrt{L}} \hat{a}^\dagger_k \\
置& \hat{a}_l = \displaystyle \sum^{N-1}_{l=0} \frac{e^{i \kappa l}}{\sqrt{N}} \hat{a}_{[\kappa]} & \hat{a}(x) = \displaystyle \sum_k \frac{e^{i k x}}{\sqrt{L}} \hat{a}_k \\
\hline
波& \hat{a}^\dagger_{[\kappa]} = \displaystyle \sum^{N-1}_{l=0}\frac{e^{i \kappa l}}{\sqrt{N}}\hat{a}^\dagger_l & \hat{a}^\dagger_k = \displaystyle \int^L_{x=0}\frac{e^{i k x}}{\sqrt{L}}\hat{a}^\dagger (x) dx \\
数& \hat{a}_{[\kappa]} = \displaystyle \sum^{N-1}_{l=0} \frac{e^{-i \kappa l}}{\sqrt{N}} \hat{a}_l & \hat{a}_k = \displaystyle \int^L_{x=0} \frac{e^{-i k x}}{\sqrt{L}} \hat{a}(x) dx \\
\hline
\end{array}
10.2 無限系
有限ではなく無限になった時も発生演算子、消滅演算子を求めることができる。ここでは結果だけを表に記載する。詳しくは西野友年著『場の理論』を参考にして欲しい。
\begin{array}{|c|c|c|}
\hline
& 有限 & 無限 \\
\hline
位 & \hat{a}^\dagger(x) = \displaystyle \sum_k \frac{e^{-i k x}}{\sqrt{L}} \hat{a}^\dagger_k & \hat{a}^\dagger (x) = \displaystyle \int^\infty_{-\infty}\frac{e^{-i k x}}{\sqrt{2 \pi}}\hat{a}^\dagger (k) dk\\
置 & \hat{a}(x) = \displaystyle \sum_k \frac{e^{i k x}}{\sqrt{L}} \hat{a}_k & \hat{a} (x) = \displaystyle \int^\infty_{-\infty} \frac{e^{i k x}}{\sqrt{2 \pi}} \hat{a}(k) dk\\
\hline
波 & \hat{a}^\dagger_k = \displaystyle \int^L_{x=0}\frac{e^{i k x}}{\sqrt{L}}\hat{a}^\dagger (x) dx & \hat{a}^\dagger_k = \displaystyle \int^\infty_{-\infty}\frac{e^{i k x}}{\sqrt{2 \pi}}\hat{a}^\dagger (x) dx \\
数 & \hat{a}_k = \displaystyle \int^L_{x=0} \frac{e^{-i k x}}{\sqrt{L}} \hat{a}(x) dx & \hat{a}_k = \displaystyle \int^\infty_{-\infty} \frac{e^{-i k x}}{\sqrt{2 \pi}} \hat{a}(x) dx \\
\hline
\end{array}