4.様々な圏の作成
圏に馴染むためにいくつかの例を挙げることにしよう。
4.1 空圏
圏の中でもっとも単純な圏は、対象も射も持たない。このため、恒等射も存在しないことになる。これは空圏(圏0)と呼ばれる。その構成を挙げておこう。
1) 対象:なし
2) 射:なし
3) ドメイン、コドメイン:なし
4) 恒等射:なし
5) 合成:なし
① 結合律:満足
② 単位律:満足
4.2 終端圏
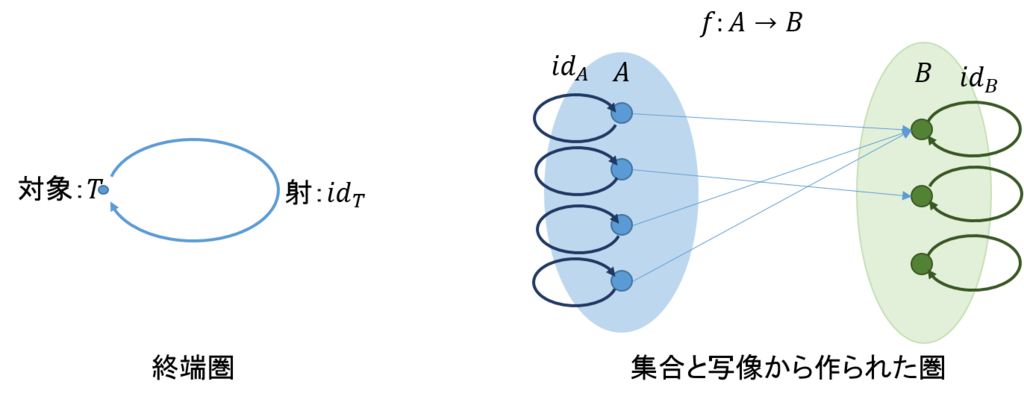
空圏に続いて単純な圏は、対象と射を一つずつ持つ終端圏(自明な圏、圏1)である。これの構成は次のようである。
1) 対象:一つ\(T\)
2) 射:一つ\(id_T\)
3) ドメイン、コドメイン:\(T\)
4) 恒等射:あり\(id_T\)
5) 合成:\(\circ\)
① 結合律:満足、即ち、\( (id_T \circ id_T) \circ id_T = id_T \circ (id_T \circ id_T) \)
② 単位律:満足、即ち、\(id_T \circ id_T=id_T\)
まだ、関手(functor)の話をしていないが、圏を対象とし、圏から圏への弧を射にすると新たな圏を構成することができる。この圏での始対象となるのが空圏で、終対象となるのが終端圏である。
4.3 二集合と関数からの圏
二つの集合\(A,B\)とその間の関数\(f\)は、それぞれの集合に恒等射を用意することで、圏にすることができる。
1) 対象:集合\(A,B\)
2) 射:関数\(f\) 、及び、恒等射と合成された射
3) ドメイン:\(A\)、コドメイン:\(B\)
4) 恒等射:\(id_A,id_B\)
5) 合成:\(\circ\)
① 結合律:関数が一つなので満足
② 単位律:\(f \circ id_A = f = id_B \circ f\)とする。
図で例を示そう(終端圏の例も同時に示す)。
4.4 グラフからの圏
射が写像だけではなく、関係も表すことができることを説明しよう。最初はグラフである。
グラフには方向のあるものとそうでないものがあるが、ここでは方向のあるものについて扱う。グラフは、節点(node)とそれを結ぶ弧(arc)によって構成される。
グラフからは、次のようにして圏が作成できる。
1) 節点(\(V_1,V_2,V_3,..\))を対象にし、弧(\(f_1,f_2,f_3,..\))を射とする。
2) さらに二つの連続している弧(片方の弧の終点と他方の弧の始点が同じ節点である)に対しては、これらを接続した弧を新たに作成し、射の中に加える。この操作を、新たな弧が作れなくなるまで繰り返す。
3) 各節点に対して、自身へ向かう弧を作成し、これを恒等射とする。
それでは例で示そう。

1) 左上は与えられたグラフである。
2) 右上は、二つの連続する弧をつなげて加えたものである。
3) 左下は三つの連続した弧をつなげて加えたものである。
4) 右下は恒等射を加えたものである。
出来上がった圏は次のようになっている。
1) 対象:節点\(U,V,W,X,Y,Z\)
2) 射:弧\(f,g,h,k,p,q,r\),及び、恒等射と合成された射
3) ドメインとコドメイン: \(f:V \rightarrow W, g:W \rightarrow X, h:X \rightarrow Y, k:U \rightarrow Z\), \( p:V \rightarrow X, q:W \rightarrow Y, r:V \rightarrow Y \)
4) 恒等射:\(id_U,id_V,id_W,id_X,id_Y,id_Z\)
5) 合成:\(p=g \circ f, \ q=h \circ g, \ r=h \circ g \circ f =h \circ p =q \circ f \)
① 結合律:\((h \circ g) \circ f = h \circ (g \circ f)\)であるので満足している。
② 単位律:\(f \circ id_V = f = id_W \circ f,...\)であるので満足している。
4.4 順序からの圏
射が関係を表す例の二番手は順序である。順序は、量や質の差によって、順序付けを行うときに使う数学の概念である。順序付けの仕方には強い場合も弱い場合もあるが、その強弱によって、順序には、前順序(preorder)、半順序(partial order)、全順序(total order)の三種類が数学の世界では用意されている。
1)前順序
ATP男子のテニスツアーも一昨日(11月6日)全て終わり、2016年度のシングルスレースの順位が確定した。錦織は、幸い、5位の位置におりロンドンで開催されるATPファイナルに出場できることとなった(上位の8人がファイナルに出場できる。今年は、ナダルが8位だが、怪我のため出場しないので、9位のティエムが繰り上げで参加になった。また、4大オープンに優勝すれば順位に関係なく出場できる)。上位5人の今年度のポイントは次のようになっている。
| 順位 | 名前 | ポイント |
|---|---|---|
| 1 | マレー | \(11,185\) |
| 2 | ジョコビッチ | \(10,780\) |
| 3 | ワウリンカ | \(5,115\) |
| 4 | ラオニッチ | \(5,050\) |
| 5 | 錦織 | \(4,705\) |
しかし、マレーとワウリンカを比べたとき、どちらが強いかと問われた時、マレーだと多くの人が答えるのではないだろうか。対戦成績を比較すると9対7だ。ジョコビッチとはさらにひらいて19対5だ。
だが、ワウリンカは次に続くラオニッチや錦織よりは強そうだ。4大タイトルの試合で2回も優勝している。
このように考えると、上位5人は3グループに分けられそうだ。最強の2人(マレー、ジョコビッチ)、追いかける1人の勇者(ワウリンカ)、次の世代を担う2人(ラオニッチ、錦織)という具合だ。
そこで、この強さの関係を前順序で表すことにしよう。前順序は、マレーとジョコビッチのように、二者間で順序をつけがたい時、即ち、どちらとも言えない時に、用いると便利である。
前順序は、量あるいは質の違いを二項関係\(\leq\)で表し、次の要件が成立することが必要とされる。ここで、\(P\)は集合とし、集合の要素同士を比較しているものとする。
1) 反射律(reflexivity):任意の\(a \in P\)に対して、\(a \leq a\)である。
2) 推移律(transitivity):任意の\(a,b,c \in P\)に対して、\(a \leq b\)かつ\(b \leq c\)であれば、\(a \leq c\)である。
\(a \leq b\)を\(a\)は\(b\)よりも強くはないということにしよう(弱いか一緒である)。このように定めると、先の5人のテニス選手の集まりを集合\(P\)とした時、彼らの関係を次図のように表すことができる。
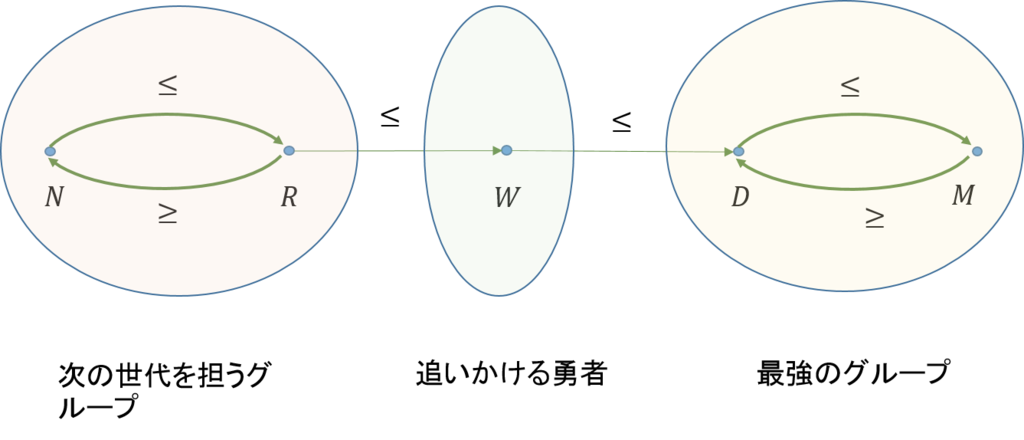
図で節点はテニス選手を表し、それぞれの姓の頭文字で表してある。また、強くはないという二項関係は弧で表してある。また、マレーとジョコビッチのように、強弱がつけがたい場合には、マレーはジョコビッチよりは強くないという関係と、ジョコビッチはマレーよりは強くないという関係の両方を用いて表した。
上の図は、先ほどのグラフと似ていないだろうか。そこで、グラフから圏を求めたときと同じ方法で、この前順序集合を圏に変えてみよう。図に示すような手順で求められる。
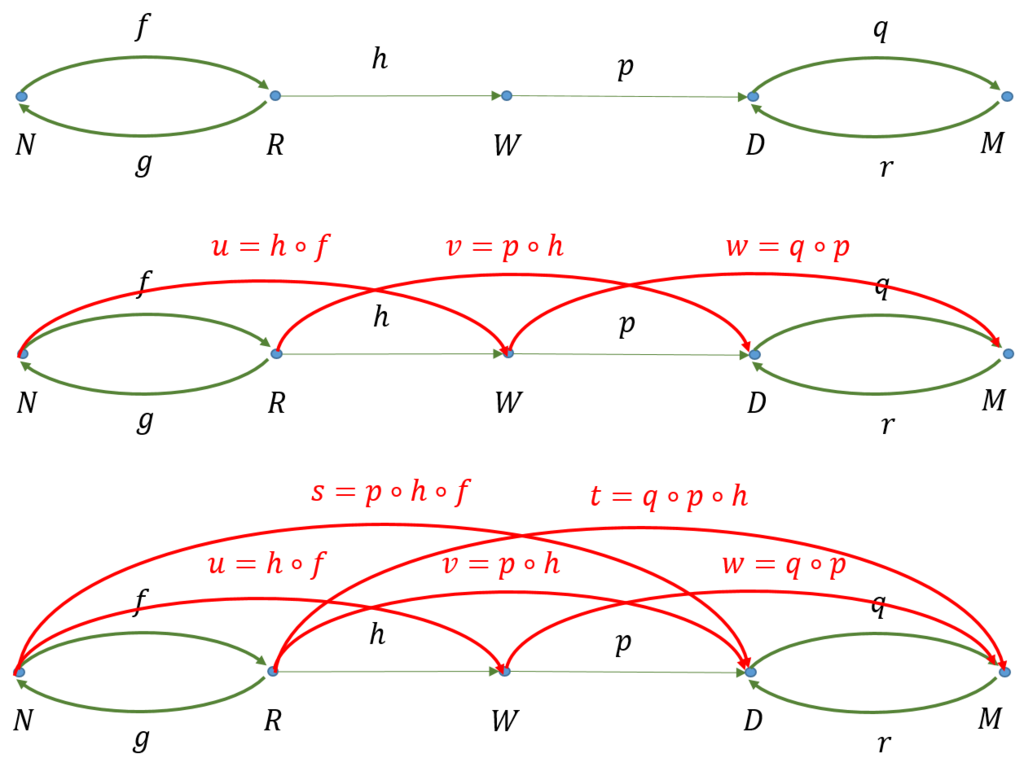

出来上がった圏は次のようになっている。
1) 対象:選手\(N,R,W,D,M\)
2) 射:強弱関係 \(f,g,h,p,q,r,s,t,u,v,w,z\)、及び、恒等射と合成された射
3) ドメインとコドメイン: \(f:N \rightarrow R, g:R \rightarrow N, h:R \rightarrow W,... \)
4) 恒等射:\(id_N,id_R,id_W,id_D,id_M\)
5) 合成:\(u=h \circ f, \ v=p \circ h, \ w=q \circ p,...\)
① 結合律:\((p \circ h) \circ f = p \circ (h \circ f),...\)であるので満足している。
② 単位律:\(f \circ id_N = f = id_R \circ f,...\)であるので満足している。
2)半順序
位相空間(topological space)を取り上げてみよう。これにはアレルギーがある人も多いことと思う。数学を得意としていた人が、大学に入ってつまずくきっかけとなりやすいのが位相空間だ。ここでは、単に集合と考えてもらっても構わないので、気楽に読んでほしい。
今、全体集合\(X\)と二つの部分集合\(A,B\)が図のように与えられたとしよう。

これから位相空間を作ることにしよう。位相空間を作るためには、開集合あるいは閉集合を用意する必要がある。ここでは、開集合を用意することにしよう。定義は次のようになっている。
位相空間は順序付けられた対\((X,T)\)である。ここで、\(X\)は集合であり、\(T\)は\(X\)の部分集合の集まりで、次の命題を満たす。
1) 空集合\(\{\}\)と\(X\)は\(T\)に属する。
2) \(T\)のメンバーのいかなる(有限でも無限でもよい)論理和も\(T\)に属する。
3) \(T\)のメンバーのいかなる有限の数の論理積も\(T\)に属する。
そこで、先に与えられた集合\(X\)と部分集合\(A,B\)から、\(T\)のメンバーを作成してみよう。
与えられた集合と空集合はメンバーに属すので、\(T\)は取り敢えず\(T=\{\{\},X,A,B\}\)となる。そこで、その他のメンバーを探してみよう。
まず、論理和の方から考えると、\(A \cup B\)が得られる。これを\(C=A \cup B\)と名付けよう。他にはなさそうである。メンバーをどのように取ってきてそれらの論理和を取ったとしても、現在のメンバーのどれかになってしまう。そこで、ここまでに得られたメンバーは\(T=\{\{\},X,A,B,C=A \cup B\}\)である。
次に論理積について考えよう。\(A \cap B\)が得られる。これを\(D=A \cap B\)と名付けよう。他にはなさそうである。ここまでに得られたメンバーは\(T=\{\{\},X,A,B,C=A \cup B,D=A \cap B\}\)である。
新たなメンバーが増えたので、もう一度論理和を考える。新しく加わるものはないので、\(T=\{\{\},X,A,B,C,D\}\)となる。

ここで、最初に与えられた集合から位相空間\((X,T)\)を作成することができた。位相空間では、\(T\)のメンバーは集合なので、含むか含まないかの関係を有する。そこで、\(A \leq B\)を\(A\)は\(B\)に含まれるということにすると、\(T\)のメンバーは順序付けすることができる。これは、以下のようなハッセ図となる。

ハッセ図は、半順序集合になっているのだが、半順序をまだ定義していない。そこで、定めておこう。前順序の時と同じように、集合\(P\)の要素同士を比較しているものとする。半順序集合は次の要件を満たすものである。
1) 反射律(reflexivity):任意の\(a \in P\)に対して、\(a \leq a\)である。
2) 推移律(transitivity):任意の\(a,b,c \in P\)に対して、\(a \leq b\)かつ\(b \leq c\)であれば、\(a \leq c\)である。
3) 反対称律(asymmetry):任意の\(a,b \in P\)に対して、\(a \leq b\)かつ\(b \leq a\)であれば、\(a = b\)である。
反対称律は、二つの要素の間には、高々一つの関係しか存在しないことをうたっている。前順序集合では、二つの要素の間に二つの関係が成り立つことを認めていた。テニス選手の例でいえば、錦織とラオニッチの間は甲乙つけがたいということで、\(N \leq R\)と\(R \leq N\)という二つの関係を用意した。
しかし、半順序集合ではこのようなことは許されない。\(N \leq R\)と\(R \leq N\)であれば、\(N = R\)となり、錦織とラオニッチは同じということになる。二人の異なる人間が同じということは何となく気持ちが悪いので、テニス選手の強さを表す時は、半順序ではなく前順序で表した。
前順序では循環(サイクル)が生じることがあるが、半順序では循環が生じない。一方向に進むグラフとなる。それでは、先のハッセ図から圏を求めてみよう。ここでは、答えだけにすると、下図のようになる。
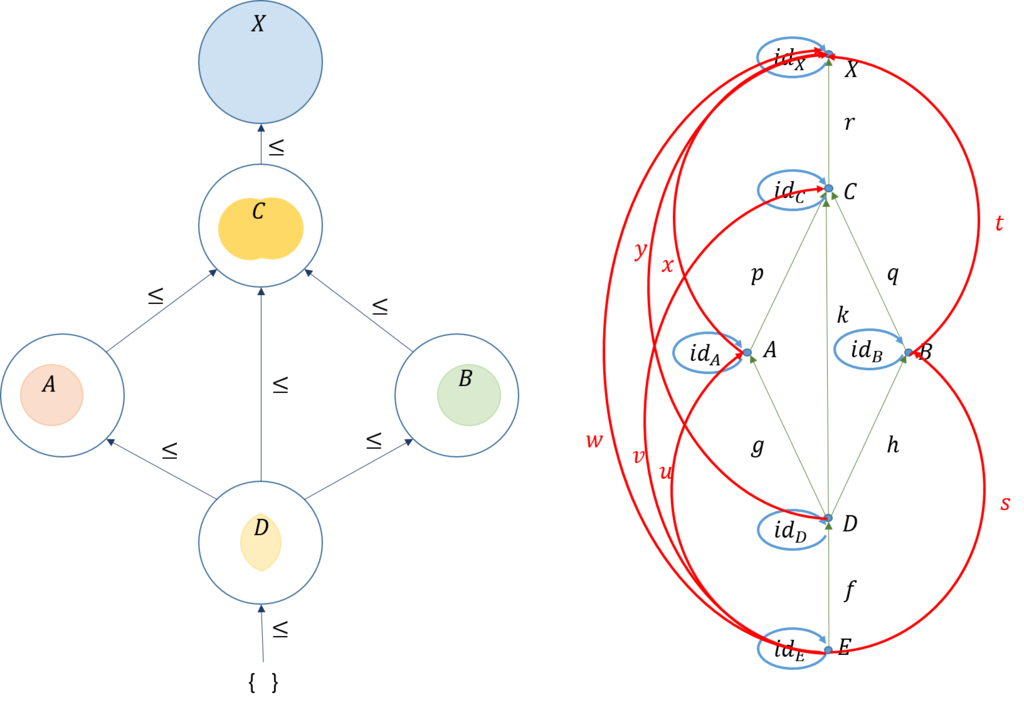
出来上がった圏は次のようになっている。
1) 対象:集合\(X,E,A,B,C,D\)
2) 射:包含関係 \(f,g,h,k,p,q,r,s,t,u,v,w,x,y\),及び、恒等射と合成された射
3) ドメインとコドメイン: \(f:E \rightarrow D, g:D \rightarrow A, h:D \rightarrow B,... \)
4) 恒等射:\(id_X,id_E,id_A,id_B,id_C,id_D\)
5) 合成:\(u=g \circ f, \ v=p \circ g \circ f, \ w=r \circ p \circ g \circ f,...\)
① 結合律:\((p \circ g) \circ f = p \circ (g \circ f),...\)であるので満足している。
② 単位律:\(f \circ id_E = f = id_D \circ f,...\)であるので満足している。
今、対象\(A\)から\(B\)への写像の集合を\({\rm Hom}(A,B)\)で表すことにしよう。
半順序の場合、任意の二つの接点を結ぶ弧は、最初に説明したように高々一つである。従って、任意の二対象\(A,B\)に対して\({\rm Hom}(A,B)\)の要素の数は高々一つである(空集合かシングルトン)。このように、任意の二対象に対して射の集合の要素の数が高々一つである圏を薄い圏(thin category)という。
薄い圏でかつ循環(サイクル)を有しないとき、全ての射はエピ射であるとともにモノ射である(証明は簡単なので試みること)。集合の世界では、単射で全射である時は、逆関数があることが保証されていた(これを双射(bijective)という)。しかし、循環(サイクル)を有しない薄い圏においては、それぞれの弧はエピ射でありモノ射であるにもかかわらず、逆向きの弧は存在しない(循環することはないため)。即ち、逆射に相当するものは存在しない。このため、エピ射・モノ射と全射・単射は完全に一致する概念ではない。
3)全順序
最後は全順序である。
全順序集合は次の要件を満たすものである。
1) 反射律(reflexivity):任意の\(a \in P\)に対して、\(a \leq a\)である(この要件は全順序律に含まれるので省いてもよい。ここでは、要件を増やしながら説明しているので、そのまま載せておいた)。
2) 推移律(transitivity):任意の\(a,b,c \in P\)に対して、\(a \leq b\)かつ\(b \leq c\)であれば、\(a \leq c\)である。
3) 反対称律(asymmetry):任意の\(a,b \in P\)に対して、\(a \leq b\)かつ\(b \leq a\)であれば、\(a = b\)である。
4) 全順序律(totality):任意の\(a,b \in P\)に対して、\(a \leq b\)か\(b \leq a\)である。
このように、全ての二つの要素に対して\(\leq\)の関係がつけられるものを全順序と呼ぶ。
建物では、どの二つの階もどちらが高いか比較できるので全順序になっている。二つの階\(A,B\)に対して、\(A \leq B\)を\(A\)は\(B\)よりも高くはないということにすると、図の階\(A,B,C,D\)について、圏を作成すると以下のようになる。
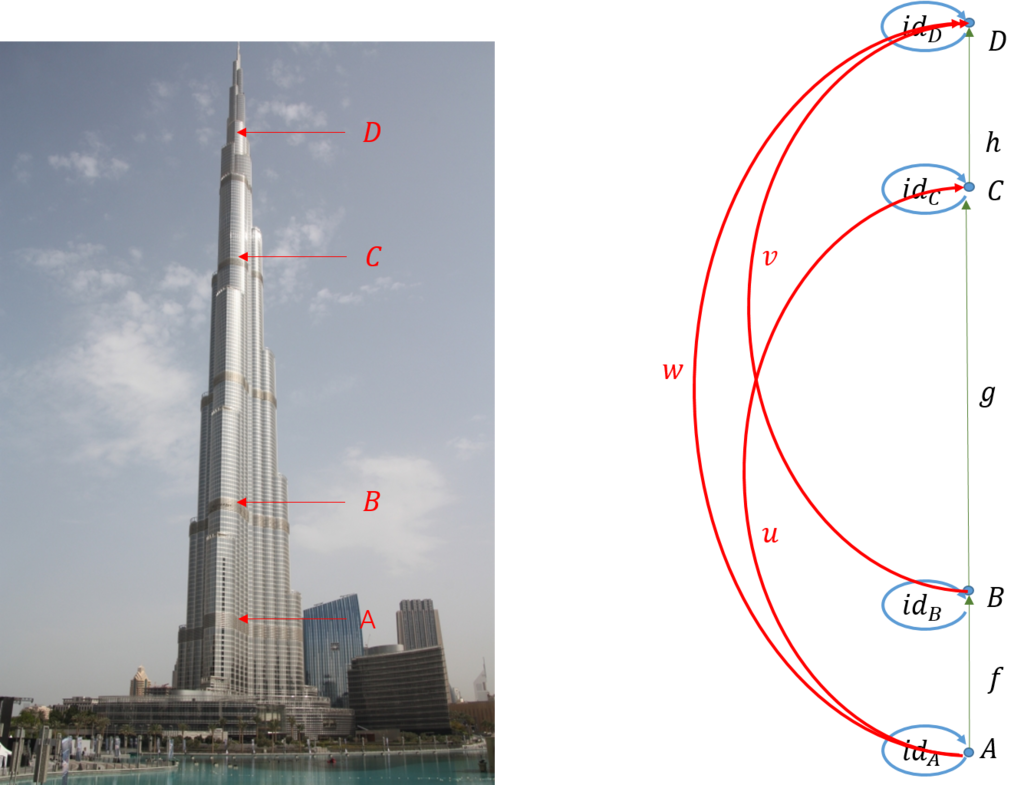
出来上がった圏は次のようになっている。
1) 対象:階\(A,B,C,D\)
2) 射:高低関係 \(f,g,h,u,v,w\),及び、恒等射と合成された射
3) ドメインとコドメイン: \(f:A \rightarrow B, g:B \rightarrow C, h:C \rightarrow D,... \)
4) 恒等射:\(id_A,id_B,id_C,id_D\)
5) 合成:\(u=g \circ f, \ v=h \circ g, \ w=h \circ g \circ f\)
① 結合律:\((h \circ g) \circ f = h \circ (g \circ f)\)であるので満足している。
② 単位律:\(f \circ id_A = f = id_B \circ f,...\)であるので満足している。
4.5 ホモトピー論からの圏
薄い圏が出てきたので、厚い圏(thick category)の例を挙げよう。二つの対象の間に複数の射があるものが厚い圏になるが、どのようなものがあるだろうか。
位相空間が出てきたので、それより、もっと近代的な数学の一分野であるホモトピー論に登場してもらおう。実は、ホモトピー論とコンピュータ科学の関係は、私事になるが、私の研究分野である。これまでにいくつかの論文を執筆してきた。当初は関心をあまり引かなかったようだが、最近では、少しずつではあるが、読んでくれる人が増えてきて喜んでいる。
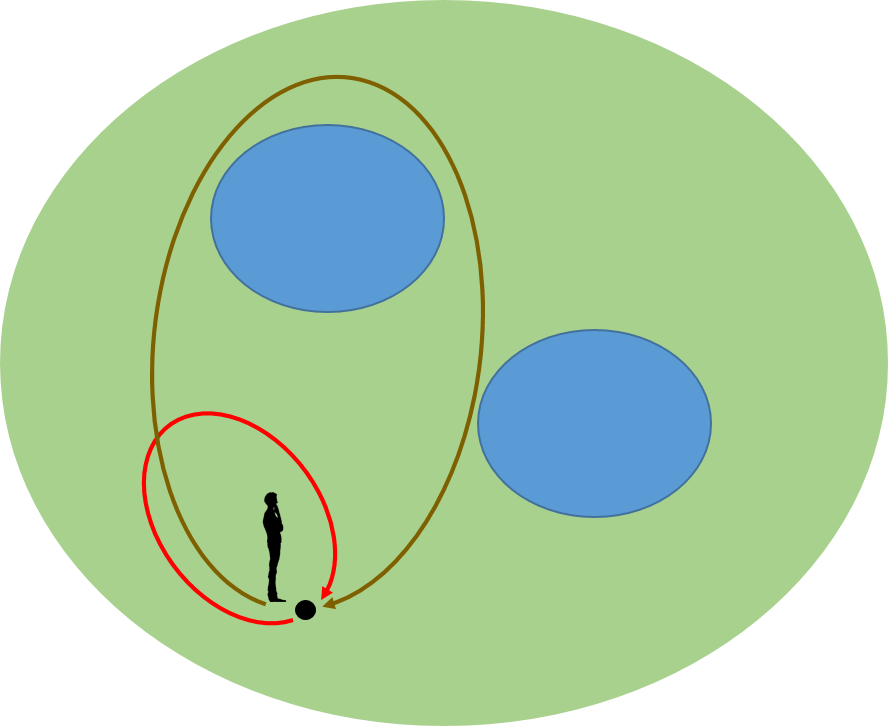
ホモトピー論にまともに立ち向かうと大変なことになるので、その考え方が伝わるように図を多用して説明しよう。下の図は公園である。公園には池が二つある。それらは青色で示してある。
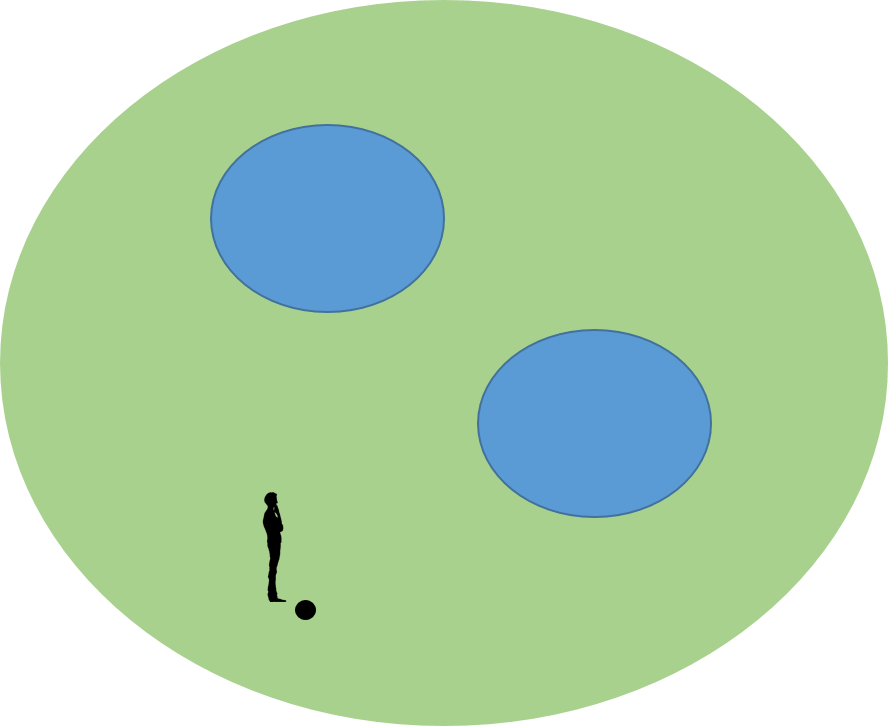
ある人が黒い地点(ここでは基点と呼ぶことにしよう)にいるとしよう。そして、一回りして基点に戻ってくることにする。例えば、池を巡らない方法は、いくつか考えられるが、例えば、図で示したように赤色と黄色の路がある。
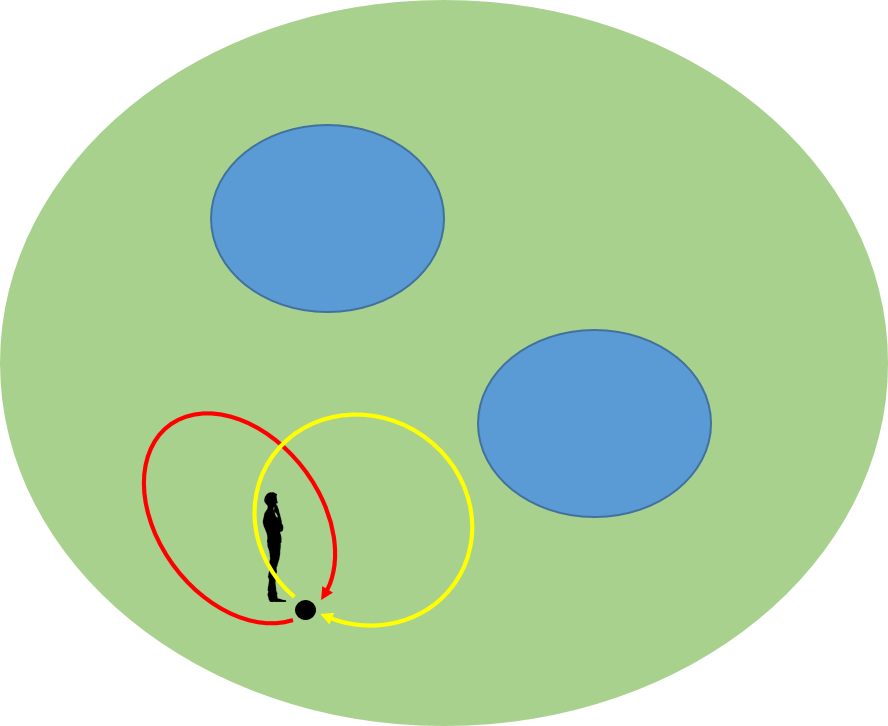
二つの路(Path)は、連続的に変化したときに相手側に行くことができれば、同値な路ということにする。少し工夫すると赤色から黄色の路に連続的に変形して移れることが分かる。
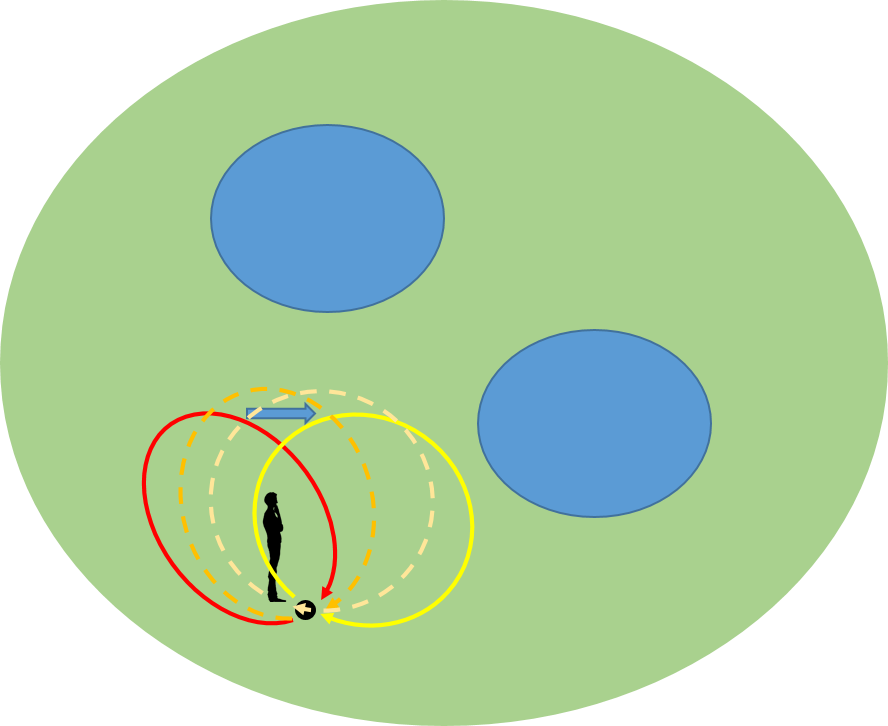
これから、池を巡ってこない路は全て同値ということになる。そこで、池を巡らない路を赤色の路で代表させることにする。
同じように考えると、左側の池を巡ってくる路はすべて同値になる。そこで、池をめぐる路の代表を茶色の路にしよう。
さらに、右の池を巡ってくる路の代表を灰色の路としよう。

これらの路は、お互いに連続な変形をして移ることができないので、独立であるという。この他に独立な路はないであろうか。二つの池をめぐる青色の路はどうであろうか。
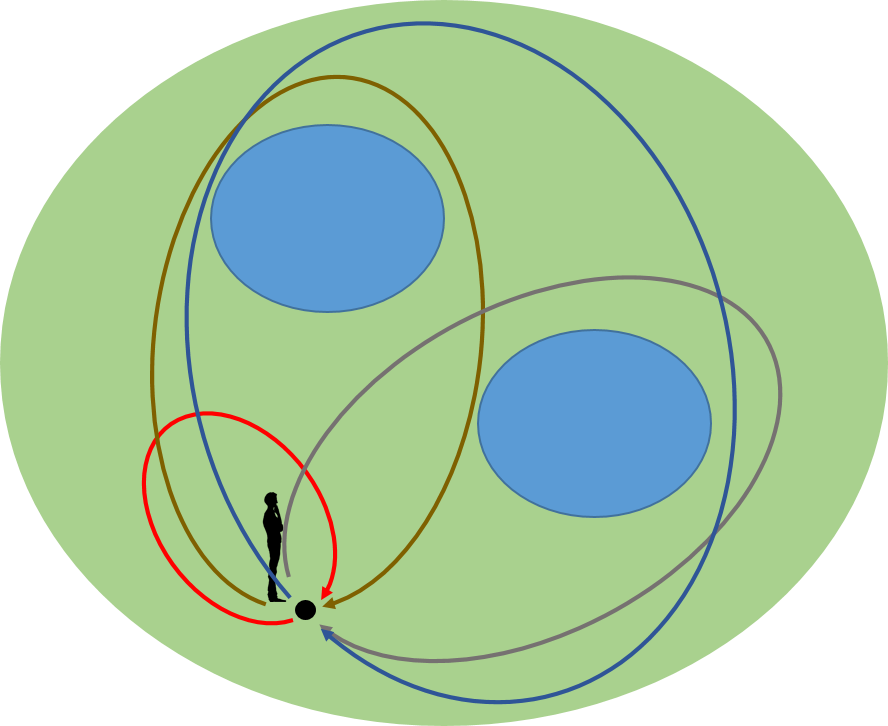
結論から言うと、青色の路は独立ではない。茶色の路を辿った後で灰色の路を辿ることで構成される合成された路を考えてみよう。この合成された路からは、下図に示すように、青色の路に連続的に変形できる路が存在する。従って、青色の路は独立とはならない。
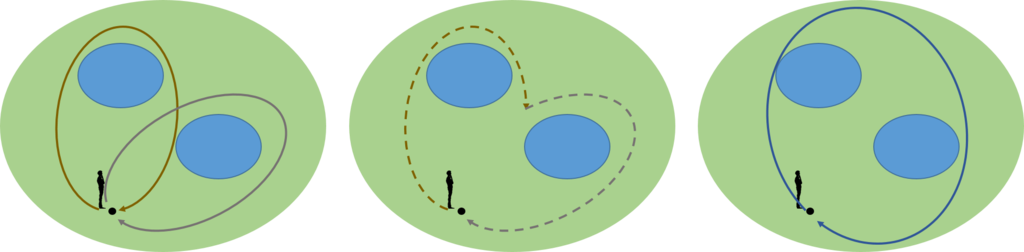
それでは、この公園でのホモトピー的な路を圏にしてみよう。図で示すと次のようになる。

図において、池を巡らない赤色の路は恒等射となる。これは、赤色の路は縮めていくと基点と一致してしまう。これは、基点から動かないことと同じなので、恒等射となる。独立な茶色と灰色の路は、射となる。これらは\(f,g\)で表すことにする。また、赤色の路と灰色の路を何回かたどるのも基点から基点へ至る路であるので、\(f\)と\(g\)を合成したもの(何回用いてもよい)も射である。
1) 対象:基点\(X\)
2) 射:路 \(f, g, s,t,u,.., \)
3) ドメインとコドメイン: \(X\)
4) 恒等射:池を巡らない路(赤色の路)\(id_X\)
5) 合成:\(\circ\)(基点を軸にして何度も路を回る)
① 結合律:満足している(路の周りかたは、結合の仕方によらない)。
② 単位律:\(f \circ id_X = f = id_X \circ f,g \circ id_X = g = id_X \circ g\)であるので満足している。
路から作られる圏は、無数の射を有していることが分かる。これは、厚い圏の例である。
次の図はトーラスである。
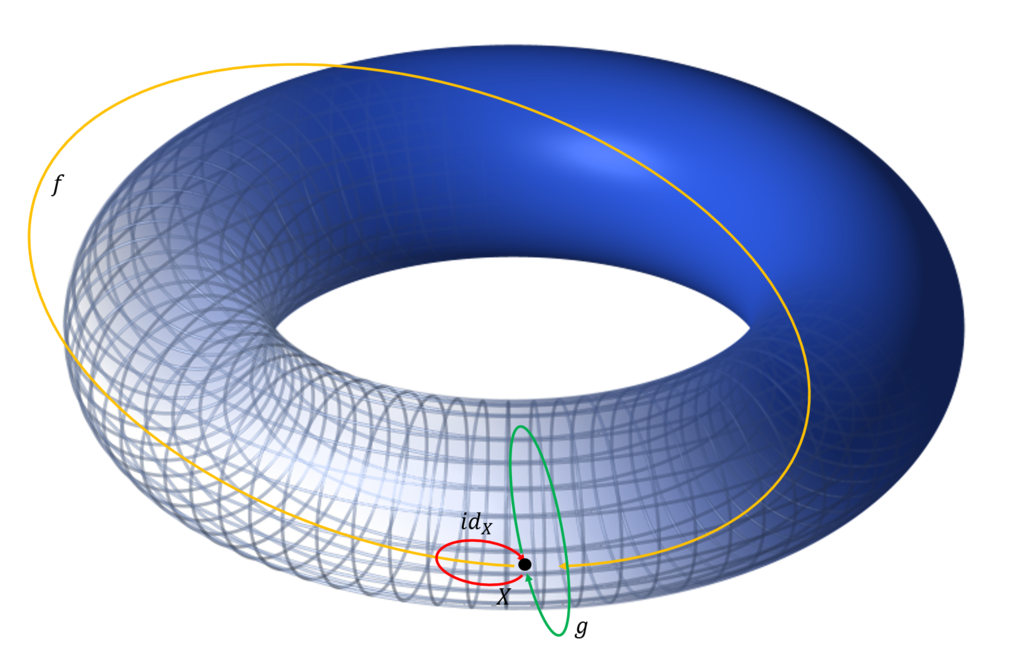
このトーラスと先ほどの公園とは全く違うものに見えるかもしれない。しかし、トーラスの一点を基点とし、そこで、路を考えてみよう。路の一つは、トーラスの穴に沿ってぐるりと回ってくるもの(図では\(f\))である。他の一つは、それとは直角方向にぐるりと回るもの(図では\(g\))である。恒等射となる路は、一周せずに戻ってくるもの(図では\(id_X\))である。他の路はこれらの合成により作られる。従って、トーラスと先ほどの公園は、同じ圏となる。トーラスは3次元で、公園は2次元であるにもかかわらず同じものとみなされる。何とも面白い世界をホモトピー論は扱う。
トーラスだけでなく、下図に示すカップもクラインの壺も同じ圏になる。

ホモトピー論の世界では基本群などを用いて物体の性質を表す。トーラスやクラインの壺の基本群は\({\mathbb Z} \times {\mathbb Z}\)である。\({\mathbb Z}\)は整数を表すが、ここでの意味は、回ってくる回数を表す。
公園の場合には、池の周りをまわる回数となる。逆回りの時は回数を減らすものと考える。従って、回数は、負を含むので、自然数ではなく整数となる。左の池と右の池を回ることは独立であったので、独立な回り方が二通りあるということで、\({\mathbb Z} \times {\mathbb Z}\)と表す。
最近のホットな数学の分野はホモトピー・タイプ論(homotopy type theory)である。この分野でタイプの研究が進むと、Haskellは多大な恩恵を受けるものと期待している。