圏論での積と余積―余積

５．５　余積

オーストラリアオープンテニス2017は、昨日、男子決勝戦が行われた。テニス界のレジェンドといわれるフェデラーとナダルが決勝で争うこととなり、これ以上、楽しませてくれる組合せはなかった。
グランドスラムの優勝回数で、二人は歴代の1位と2位である。テニス史上、最も強いプレーヤーの対決だ。二人とも準決勝では長い試合を戦ったので、決勝戦に疲れが残っていないのだろうかと心配していたが、そのような心配は全く不要で、信じられないようなスーパープレーを余すところなく見せてくれ、感動したの一言に尽きる試合であった。

勝敗を決めることを雌雄を決するという。「雌雄を決する」という用語は『史記・項羽本記』のなかで、「願與漢王挑戦決雌雄(願わくは漢王との戦いを挑み、雌雄を決せん)」と出てくる。一般に、動物は雄が強く、雌が弱いものとされていて、いずれが雄でいずれが雌であるかを決めようということから来た言葉だそうだ。

フェデラーとナダル、ジョコビッチとマレー、そして願わくば、錦織とラオニッチが、雌雄を決する最高の場面をこれからもたくさん提供してくれるといいなあと思う。

これから話をする余積は、概念的には雌雄に相当するものだ。

積の圏(product category)は次の条件を満たすものであった。
1) 積と呼ばれる対象が一つ存在する。これを\(C\)とする。
2) \(C\)には投影(Projection)と呼ばれる二つの射\(p,q\)が存在する。これらは\(C\)をそれぞれ\(A,B\)に投射する。
3) \(C\)以外の任意の対象\(C'\)は\(A,B\)へ投影する射\(p',q'\)を持つ。そして、ただ一つの射\(m\)が存在し、これは\(p'=p \circ m,q'= q \circ m\)を満たす。
\(C\)が上記を満たす時、これは\(A,B\)の余積と呼ばれ\(C=A \times B\)と記される。

積の圏での射の方向を逆にすると、双対関係にある、余積の圏(coproduct category)を得る。図で示すと以下のようになる。

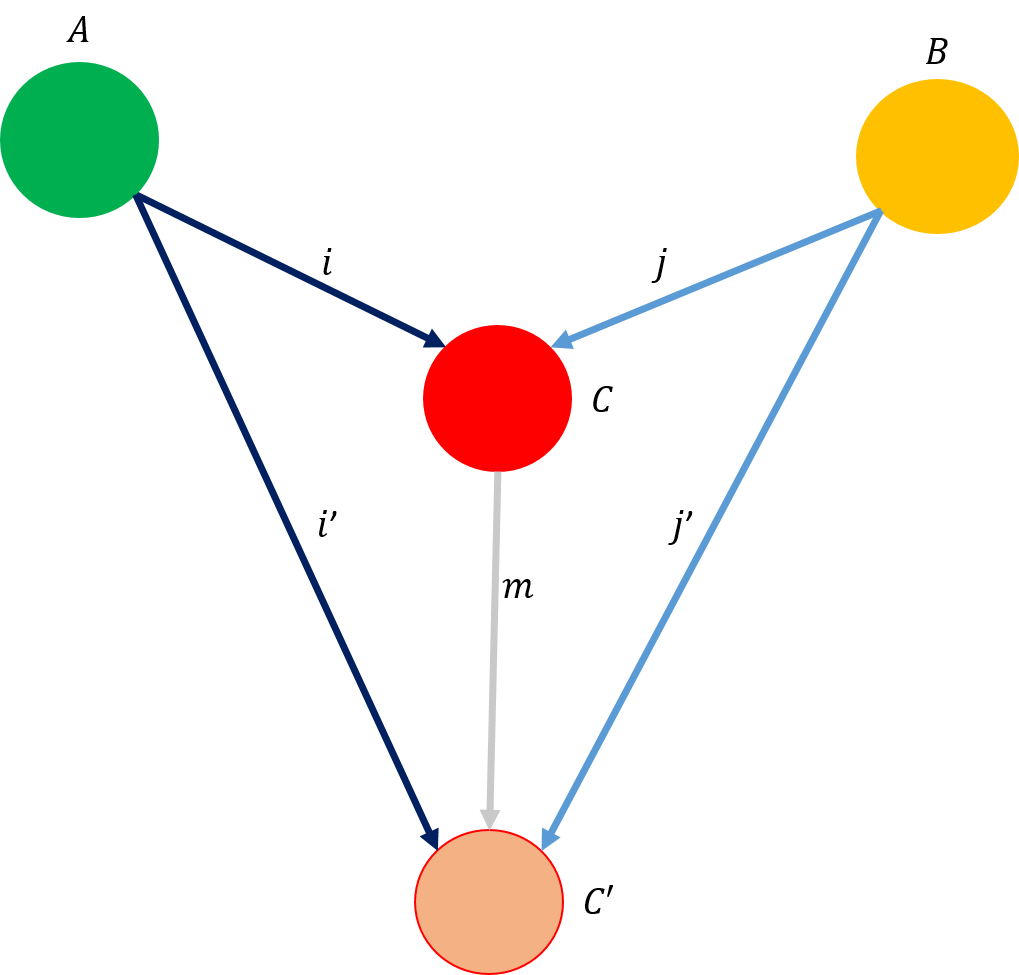
余積の圏を定義すると次のようになる。
1) 余積と呼ばれる対象が一つ存在する。これを\(C\)とする。
2) \(C\)には注入(Injection)と呼ばれる二つの射\(i,j\)が存在する。これらはそれぞれ\(A,B\)から\(C\)に注入する。
3) \(C\)以外の任意の対象\(C'\)は\(A,B\)から注入する射\(i',j'\)を持つ。そして、ただ一つの射\(m\)が存在し、これは\(i'=m \circ i,j'= m \circ j\)を満たす。
\(C\)が上記を満たす時、これは\(A,B\)の積と呼ばれ\(C=A + B\)と記される(\(+\)の代わりに\(\oplus\)や\(\amalg\)が使われることもある)。

余積の圏とはどのようなものであろうか。二つの対象を注入して一つの対象を作るというのがその趣旨である。レトリックな世界で少し楽しんでみよう。

先ほどまで、雌雄の話をしていたので、ここでは、男女のカップルを考えてみよう。対象\(A\)を男だけを集めた対象にする。対象\(B\)を女だけを集めた対象とする。そして、対象\(C\)はカップルを集めた対象とする(ここは進行中のカップルだけでなく、可能なカップルをすべて含む。余談だが、何となく、\(C=A \times B\)ではなく、自由度の高そうな、\(C=A + B\)というような気がしないだろうか)。この時、\(i,j\)はカップルを構成するための関数として定義できる。それでは、対象\(C'\)は何だろう。カップルが住む家の集まりを対象\(C'\)にしてはどうだろうか(但し、それぞれのカップルは一軒だけ家を持つこととする。二軒以上持つと関数を定義するのが厄介になる）。このようにすると、射\(m\)は一意に決めることができ、また、\(i'=m \circ i\)と\(j'= m \circ j\)を満足する。

積の圏はHaskellでは対、あるいは、タプルであった。余積の圏はHaskellではなんであろうか。Eitherである。これは次のように定義されている。

Prelude> :i Either
data Either a b = Left a | Right b 	-- Defined in ‘Data.Either’

ここで、\(i\)に相当するものはLeftであり、\(j\)に相当するものはRightである。少し利用してみよう。友人たちの名前を利用させてもらうと次のようになる。

Prelude> let a1 = Left "Peter"
Prelude> let a2 = Left "Mike"
Prelude> let b1 = Right "Leonie"
Prelude> let b2 = Right "Jenny"
Prelude> :t a1
a1 :: Either [Char] b
Prelude> :t b1
b1 :: Either a [Char]

それでは、家を求める関数\(m\)を定義してみよう。最初の二組は法律上のカップル。最後は、実際にそうなると大変なことになる。英語ではaffairといわれるものだ。

Prelude> let m (Left a) (Right b) = "Home of " ++ a ++ " and " ++ b ++ "."
Prelude> m a1 b1
"Home of Peter and Leonie."
Prelude> m a2 b2
"Home of Mike and Jenny."
Prelude> m a1 b2
"Home of Peter and Jenny."

積は\(\times\)で余積は\(+\)で表した。これらの記号は、乗算と加算で用いられるものである。このような記号が使われているからには、関係があるはずである。これについて次の記事で述べる。