6.8 余積をファンクタで実現する
前回の記事では関手を利用しての積と余積を定義する中で\(Identity\)を用いたが、その詳しい説明はしなかった。そこで、ここでは、まず、データ型\(Identity\)の定義から話を始めよう。関手\(Identity\)の可換図式は下図のようになる。
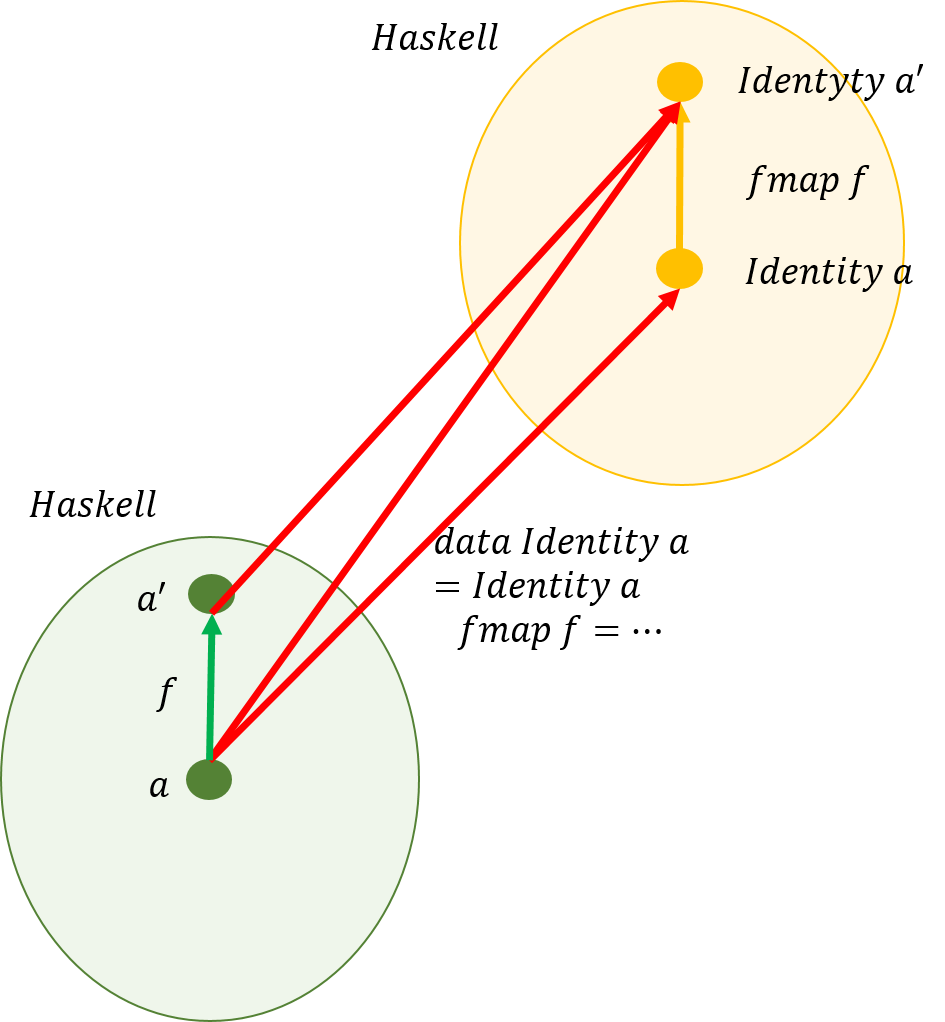
これを参考にしてHaskellで\(Identity\)のデータ型とファンクタを実現すると次のようになる。
data Identity a = Identity a deriving (Eq, Show, Read) instance Functor Identity where fmap f (Identity a) = Identity (f a)
終対象への写像に似ている関数で、一つの値\(c\)に写像する定数関数\(const\)と呼ばれるものがある。これを下図のように関手として利用してみよう。

\(Const\)のデータ型とファンクタは次のようになる。
data Const c a = Const c deriving (Eq, Show, Read) instance Functor (Const c) where fmap f (Const c) = Const c
少し利用してみよう。
*Main> a = Identity 4 *Main> fmap (*3) a Identity 12 *Main> fmap (+6) a Identity 10 *Main> b = Const 3 *Main> fmap (*3) b Const 3 *Main> fmap (+6) b Const 3
今得た二つの可換図式を左右を逆にして重ねてみよう。

この可換図式は定数\(Const \ c\)と値\(Identity \ a\)との余積と見ることができる。しかも、余積はファンクタとしての\(Identity\)と\(Const\)により実現されている。
それでは、\(Const \ c\)を\( ( ) \)で置き換えてみよう。

これも余積である。Haskellは余積を\(Either\)で表していたので、これは\(Either \ (Const \ ()) \ (Identity \ a)\)と書くことができる。
これは何かに似ていないだろうか。\(Maybe\)は値を持たないか値を持つかのいずれかであった。値を持たない場合には\(Nothing\)で表し、持つ場合には\(Just \ a\)で表した。そこで、これを今得た\(Either\)に当てはめてみよう。\(Nothing\)を\(Const \ ( )\)と、\(Just \ a\)を\(Identity \ a\)と考えてみよう。相互に表現法が違うだけで同じものであることが分かる。そこで、\(Either \ (Const \ ()) \ (Identity \ a)\)をタイプを用いて次のように\(Maybe'\)で言い換えてみる。
type Maybe' a = Either (Const () a) (Identity a)
少し利用してみよう。変数のデータ型を定めながらの利用になるが以下の様である。
*Main> a = Identity (3 :: Integer) *Main> b = Right a :: Maybe' Integer *Main> c = Const () :: Const () Integer *Main> d = Left c :: Maybe' Integer *Main> :t a a :: Identity Integer *Main> a Identity 3 *Main> b Right (Identity 3) *Main> c Const () *Main> d Left (Const ()) *Main> :t a a :: Identity Integer *Main> :t b b :: Maybe' Integer *Main> :t c c :: Const () Integer *Main> :t d d :: Maybe' Integer *Main> :i a a :: Identity Integer -- Defined at <interactive>:9:1 *Main> :i b b :: Maybe' Integer -- Defined at <interactive>:10:1 *Main> :i c c :: Const () Integer -- Defined at <interactive>:11:1 *Main> :i d d :: Maybe' Integer -- Defined at <interactive>:12:1
このことからも、\(Maybe\)と\(Either\)は同じ概念を表していることが分かる。沢山のファンクタについて説明してきたが、次は反関手の話をする。