1.5 極限の定義
前回の記事で、インデックス圏から錐を作成する方法を示した。
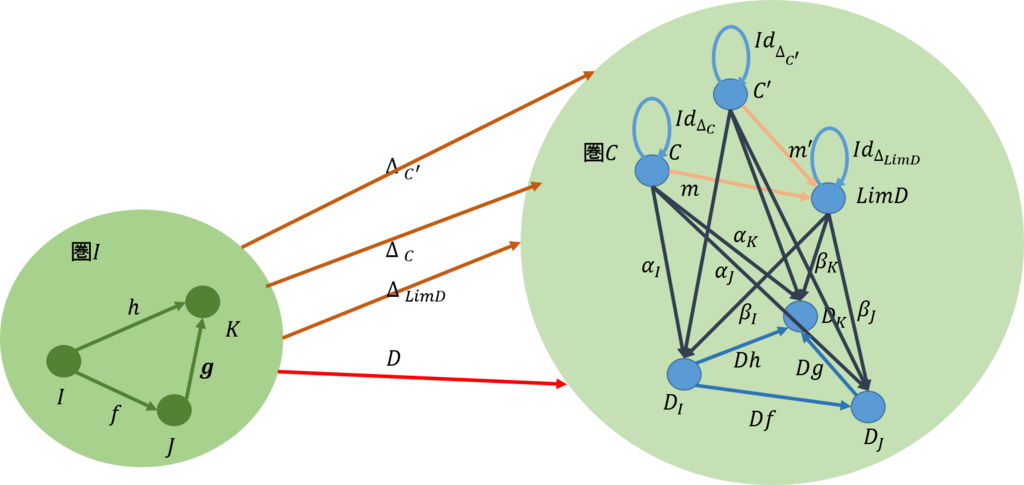
上図で、関手\(D\)によって、インデックス圏\(\mathcal{I}\)での三角形(頂点が対象、辺が射)が、圏\(\mathcal{C}\)に移され、これから作成される(三角)錐の底辺を形成する。この底辺の各頂点は\(\mathcal{I}\)の対象を、また、各辺は\(\mathcal{I}\)の射を、関手\(D\)によって、それぞれ移したものである。
また、上の図で、圏\(\mathcal{I}\)の三角形の頂点、即ち、対象の全てを、関手\(\Delta_C\)によって、一つの対象\(C\)に移した。このとき、圏\(\mathcal{I}\)の三角形の辺、即ち、射の全ては、\(\Delta_C\)によって、\(C\)での恒等射\(Id_{\Delta_C}\)に移される。
関手\(\Delta_C\)と関手\(D\)の間で、自然変換\(\alpha=\{\alpha_I,\alpha_J,\alpha_K\}\)が存在するなら、三角錐\(C,D_I,D_J,D_K\)が構成され、その側面は可換となっている。即ち、\(Df \circ \alpha_I = \alpha_J\), \(Dg \circ \alpha_J = \alpha_K\),\(Dh \circ \alpha_I = \alpha_K\)である。
同様に、関手\(\Delta_C’\)からも同じように側面が可換となっている三角錐を構成できる。
このような三角錐がいくつもできるであろう。その中で、極限と呼ばれるものを定義することにしよう。得られた三角錐の中から一つの頂点を選び、これを\(LimD\)と呼ぶことにしよう。\(LimD\)を頂点とする三角錐が次の条件を満たす時、極限という。なお、この三角錐での自然変換を\(\beta=\{\beta_I,\beta_J,\beta_K\}\)とする。
[条件] 任意の(三角)錐の頂点\(C\)に対して
1. 一意的に定まる射\(m: C \rightarrow LimD \)が存在し、
2. 圏\(\mathcal{I}\)の全ての対象\(i\)に対して、\(\beta_I \circ m = \alpha_I\)となる。即ち、上記の図の場合には、\(\beta_I \circ m = \alpha_I\),\(\beta_J \circ m = \alpha_J\),\(\beta_K \circ m = \alpha_K\)である。
説明では、理解しやすくするために、インデックス圏を三角形としたが、多角形でも構わない。さらには、辺の数が無限となった円でも構わない。
なお、このような射\(m\)は分解射(factorization)と呼ばれる。
また、\(\beta_I,\beta_J,\beta_K\)は、専門用語を用いれば、モノ射である。モノ射は次のように定義されている。射\(f:X \rightarrow Y\)がモノであるとは、任意の射\(g_1,g_2:Z \rightarrow X\)に対して、\(f \circ g_1= f \circ g_2\)であるならば、\(g_1=g_2\)が成り立つ。