1.7 錐と極限のさらなる抽象化
前回の記事で、錐は二つの異なる方法で作成できることが分かった。一つは、錐の頂点から錐の底面への写像を自然変換で与えるものである。もう一つは、求める錐の頂点から極限の錐の頂点への射を与えるものである。
前回は、さらに、この二つの方法は同型の写像を与えることも示した。写像が同型であるので、この間で自然変換を定義できるようになる。求める錐の頂点を\(C\)としたとき、この始自然変換を\(\alpha_C\)で表すことにしよう。図で示すと次のようになる。
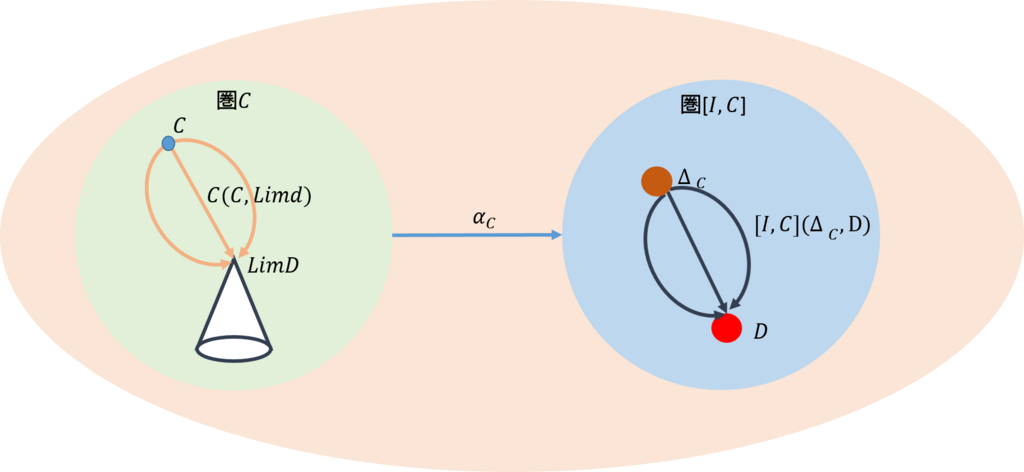
ここまでが前回の話である。
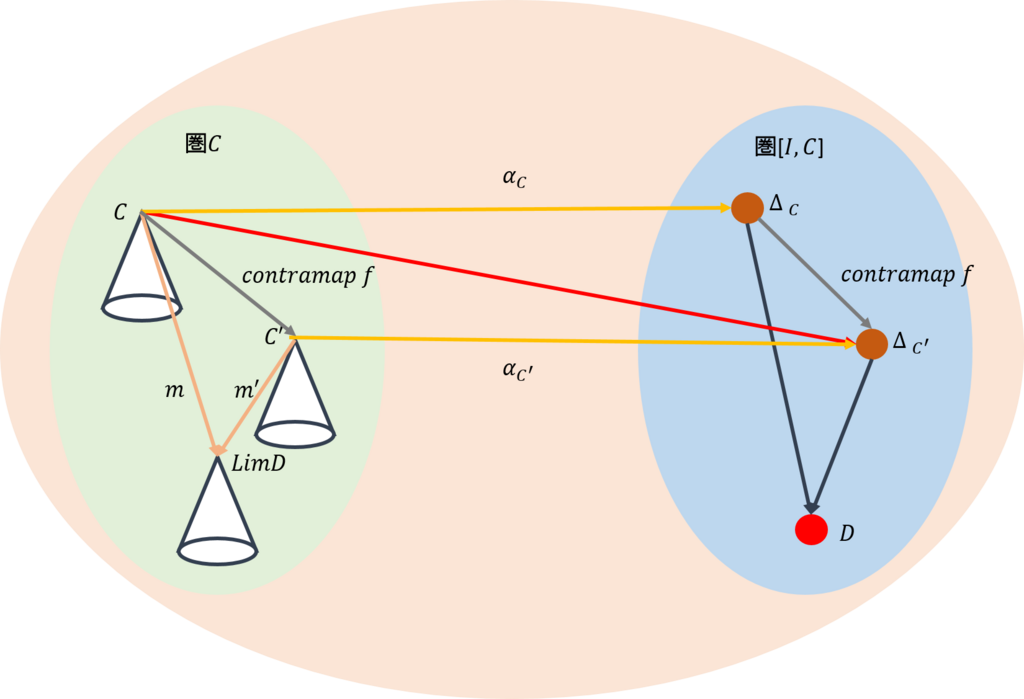
それでは、この方法によって、\(C\)を頂点とする錐が得られたとする。この得られた錐から、別の錐\(C’\)を求めるにはどのようにしたらよいであろうか(下図)。
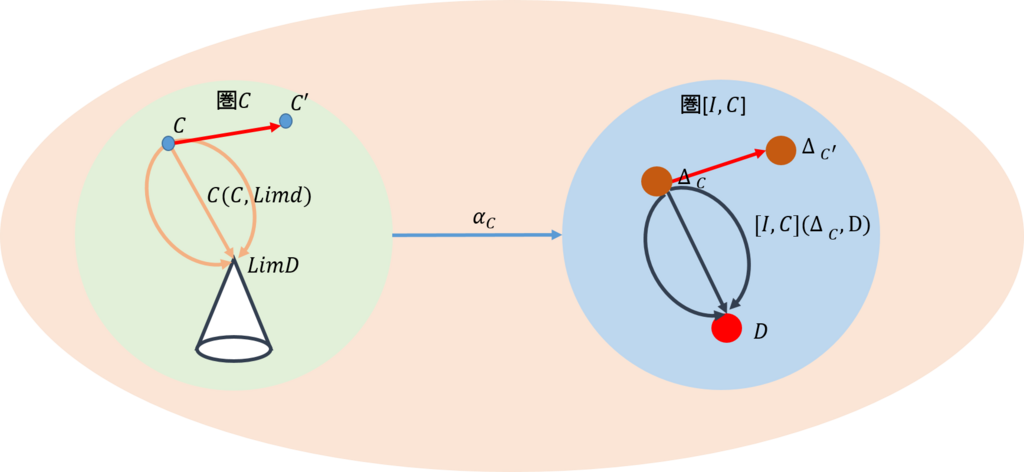
なお、\(C\)と\(C’\)には、\(f:C’ \rightarrow C\)の関係があるものとする。ここで、\(f:C \rightarrow C’\)でないことに注意しておいてほしい。訳はすぐに分かる。
これの可換図式を求めると次のようになる。なお、関手は射も写像するが、その時移す側と移される側で向きが同じとき、この関手は共変関手(contravariant)と呼ばれる。それに対して、反対になるときは、関手は反変関手(contravariant)と呼ばれる。そこで、上の図では反変関手なので、\(f\)が移されている先を\(contramap \ f\)とした。
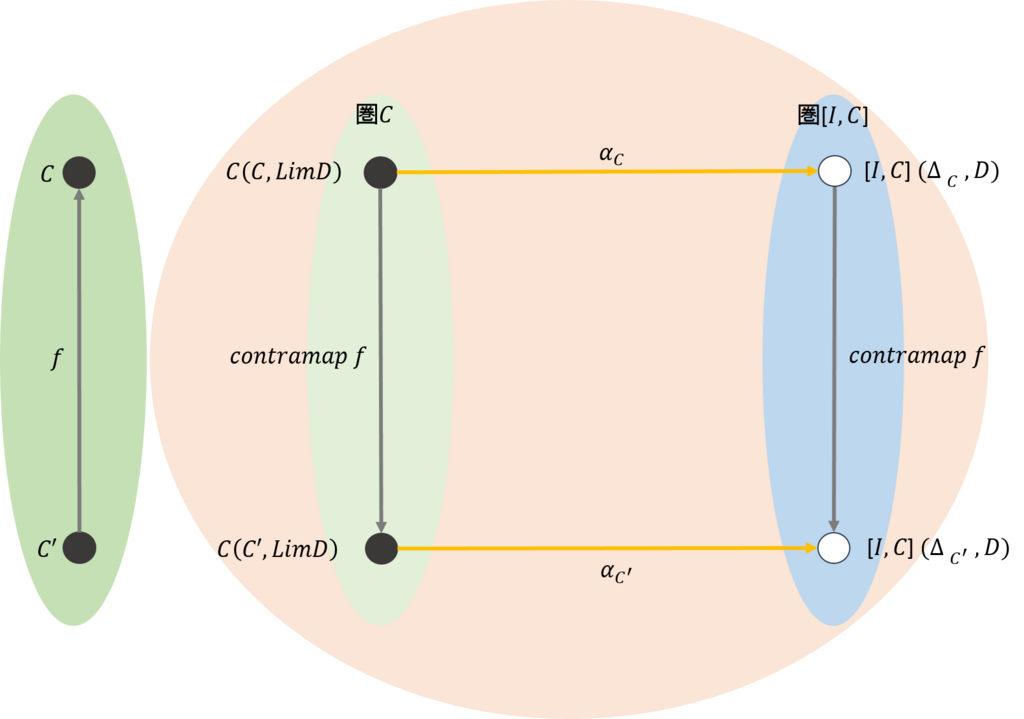
上図の可換図式で\(\mathcal{C}(C,LimD)\)は射の集合であるので、それを\(u: C \rightarrow LimD\)と表すことができる。また、\(\mathcal{C}(C’,LimD)\)を\(v: C' \rightarrow LimD\)と表すことができる。ところで、\(f:C' \rightarrow C\)なので、\(v=u \circ f\)となる。
また、\([\mathcal{I,C}](\Delta_C,D)\)は自然変換である。従って、これはインデックス圏の対象\(I\)毎に、\(\mu_I:C \rightarrow D_I\)と表すことができる。同様に、\([\mathcal{I,C}](\Delta_{C'},D)\)を\(\nu_I:C’ \rightarrow D_I\)と表すことができ、先ほどと同様に、\(\nu_I =\mu_I \circ f\)となる。
この関係を示したのが下図である。
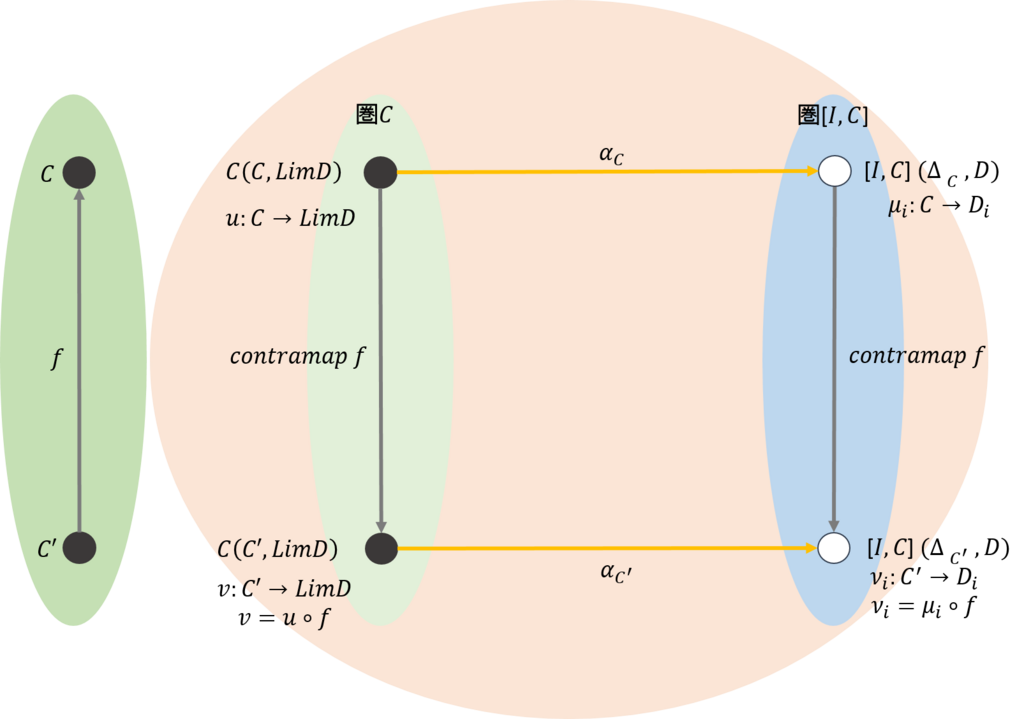
この可換図式から、圏\(\mathcal{C}\)での頂点を\(C\)とする錐から、圏\([\mathcal{I,C}]\)での頂点\(C’\)の錐を求めるには、圏\(\mathcal{C}\)で\(C’\)に移動してから圏\([\mathcal{I,C}]\)にジャンプしてもよいし、圏\(\mathcal{C}\)から圏\([\mathcal{I,C}]\)にジャンプしてから\(C’\)に移動してもよいと言っている。これを図で表すと以下のようになる。
極限の理論的な話はここまでだが、次回はいくつか例を示そう。