7.2 余米田の補題
米田の補題では、共変\(\rm{Hom}\)関手\(\mathcal{C}(A,-)\)を用いていたが、これを反変\(\rm{Hom}\)関手\(\mathcal{C}(-,A)\)に変えたのが、余米田の補題となる。
次のようになる。局所的に小さな圏\(\mathcal{C}\)と集合の圏\(\mathbf{Set}\)、これらによって作られる関手圏\([\mathcal{C},\mathbf{Set}]\)を考える。今、任意の対象\(A \in \mathcal{C}\)と任意の関手\(F: \mathcal{C} \rightarrow \mathbf{Set}\)に対して、
\begin{eqnarray}
[\mathcal{C},\mathbf{Set}](\mathcal{C}(-,A),F) \cong F(A)
\end{eqnarray}
が成り立つ。ただし、\(\mathcal{C}(-,A): \mathcal{C} \rightarrow \mathbf{Set}\)は関手であり、\([\mathcal{C},\mathbf{Set}](\mathcal{C}(-,A),F)\)は\(\mathcal{C}(-,A)\)から\(F\)への自然変換である。
図で示すと次のようになる。
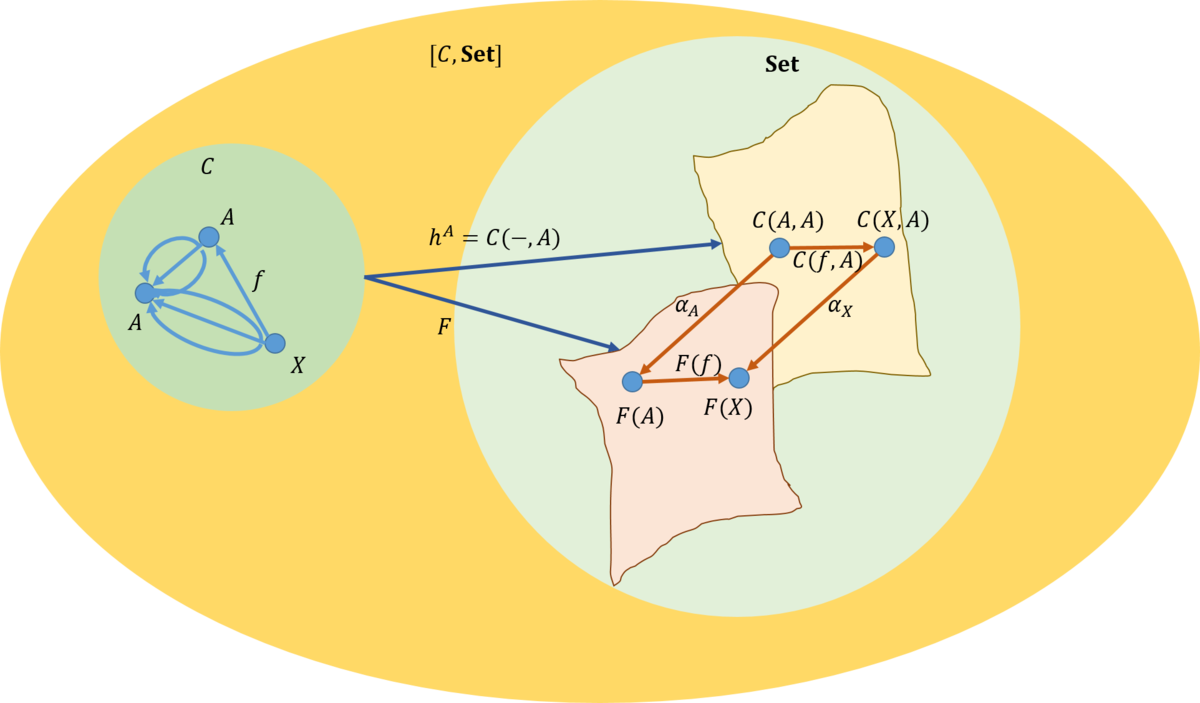
証明は、米田の補題でのそれを利用すると、同じように行える。
7.3 米田の埋め込み
米田の補題は、米田の埋め込みを証明するために利用したものである。米田の補題で、関手\(F\)を反変関手にしたものを、前回の記事で紹介した。
\begin{eqnarray}
[\mathcal{C},\mathbf{Set}](\mathcal{C}(A,-), \mathcal{C}(B,-)) \cong \mathcal{C}(B,A)
\end{eqnarray}
これが米田の埋め込みと呼ばれている。図で表すと次のようになる。
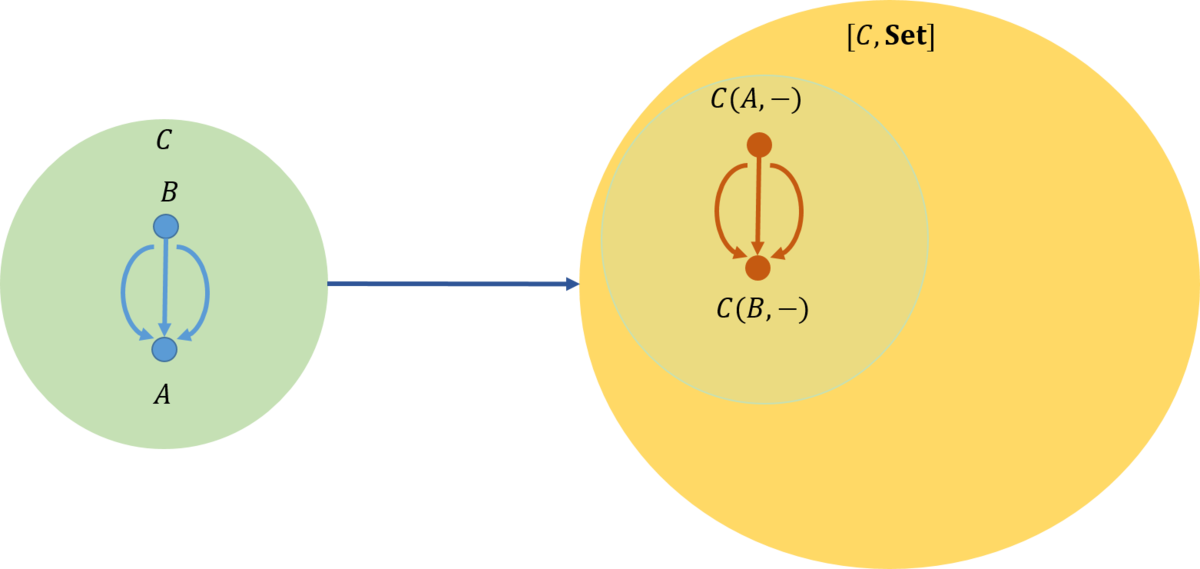
米田の埋め込みは\(B\)から\(A\)への\({\rm Hom}\)集合と、\(\mathcal{C}(A,-)\)から\(\mathcal{C}(B,-)\)への\({\rm Hom}\)集合とは同型であるといっている。
これは、局所的に小さな圏\(\mathcal{C}\)の任意の二つの対象\(A\)と\(B\)を選び、また、その対象間の\({\rm Hom}\)集合を\(\mathcal{C}(A,B)\)とした時、関手圏\([\mathcal{C},\mathbf{Set}]\)にはこれと同型の構造が存在する。即ち、\(A\)に対して対象\(\mathcal{C}(B,-)\)が、また、\(B\)に対して対象\(\mathcal{C}(A,-)\)が対応し、\(\mathcal{C}(A,B)\)に対して、対象\(\mathcal{C}(B,-)\)から対象\(\mathcal{C}(A,-)\)への同型の\({\rm Hom}\)集合が存在する。
従って、米田の埋め込みは、局所的に小さな圏\(\mathcal{C}\)の構造が、関手圏\([\mathcal{C},\mathbf{Set}]\)に忠実に(faithful)しかも充満に(full)埋め込まれることを述べている。なお、忠実は単射であることを言い、充満は全射であることを言う。
米田の埋め込みを利用してみよう。
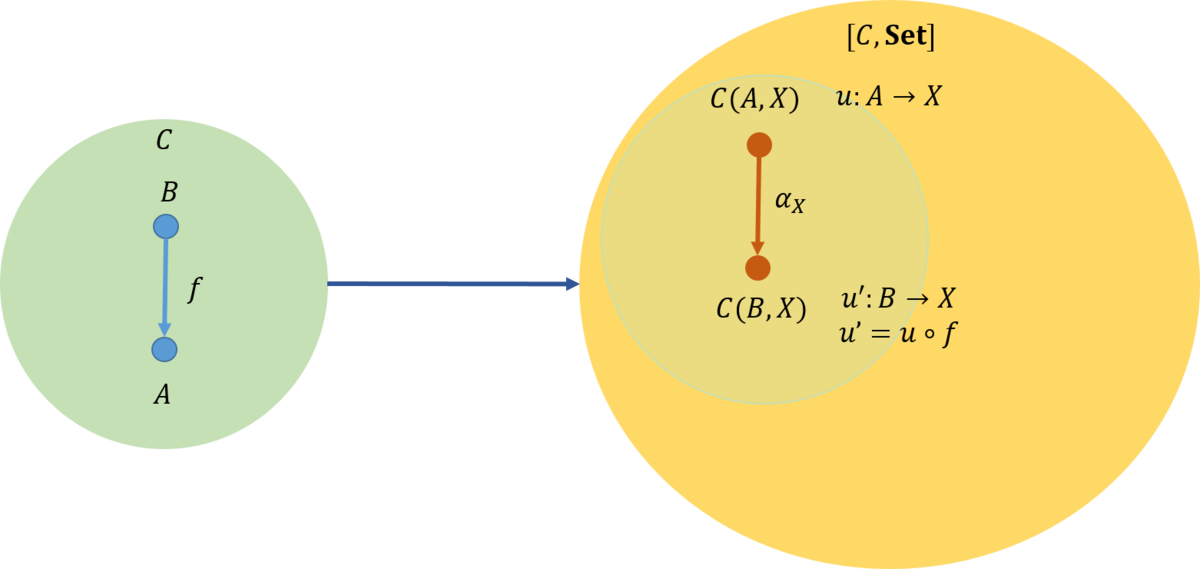
例1
今、\(f \in \mathcal{C}(B,A)\)と\(u \in \mathcal{C}(A,X)\)が図のように与えられたとしよう。この時、自然変換\(\alpha_X\)を求めよう。これには、\(u’ \in \mathcal{C}(B,X)\)を求めればよいが、\(u’ = u \circ f\)となることは自明である。
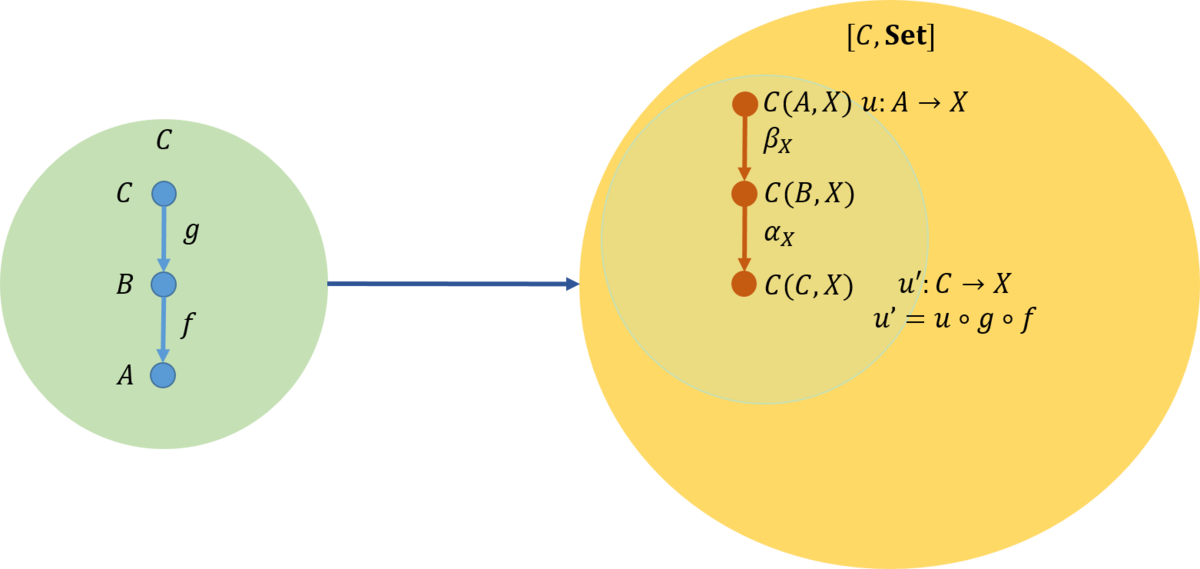
参考のために、三つの対象の場合も図に挙げておく。対応関係を確認して欲しい。
例2
関手圏\([\mathcal{C},\mathbf{Set}]\)において、\(\mathcal{C}(A,-)\)と \(\mathcal{C}(B,-)\)が同型の時、小さい圏\(\mathcal{C}\)において、\(A\)と\(B\)は同型である。また、逆も成り立つ。証明は試みて欲しい。
例3
前順序(preorder)集合を考えてみよう。これは、任意の二つの要素に対して、\(a \leq b\)であれば矢印があり、そうでなければ矢印はないという性質を有している。
それでは、前順序集合に対して余米田の埋め込みを利用してみよう。
\begin{eqnarray}
[\mathcal{C},\mathbf{Set}](\mathcal{C}(-,A), \mathcal{C}(-,B)) \cong \mathcal{C}(A,B)
\end{eqnarray}
今、右辺が\(A \leq B\)であったとする。この時、\({\rm Hom}\)集合\(\mathcal{C}(A,B)\)での関数の数が1であることに注意して、これを満たす左辺を求めて見よう。
今、任意の\(X\)に対して\(X \leq A\)の時は、前順序の関数が一つ存在するので\({\rm Hom}\)集合としての\(\mathcal{C}(-,A)\)は関数の数は1になり、そうでないときは前順序の関数が存在しないので空\(\phi\)となる。\(X \leq B\)についても同じである。なお、ここでは、\(X\)は\(A\)でもなく\(B\)でもないとする。
左辺の\({\rm Hom}\)集合での関数の数が1なので、\({\rm Hom}\)集合としての自然変換\([\mathcal{C},\mathbf{Set}](\mathcal{C}(X,A), \mathcal{C}(X,B))\)も1になるはずである。自然変換は、\(\mathcal{C}(X,A) \rightarrow \mathcal{C}(X,B))\)での組み合わせとなる。従って、以下の四つの組合せのどれかということになるが、どれが該当するのであろうか。この中の、一つだといっている。
\begin{eqnarray}
id_\phi: \phi \rightarrow \phi \\
absurb: \phi \rightarrow 1 \\
id_1: 1 \rightarrow 1 \\
prohibit: 1 \rightarrow \phi
\end{eqnarray}
この中で、4番目は関数が値を持たないこととなり関数ではない。従って、最初の三つが候補となるが、正しいのは3遍目となる。これは、\(X \leq A\)ならば、\(X \leq B\)であるといっている。これを示したのが下図である。
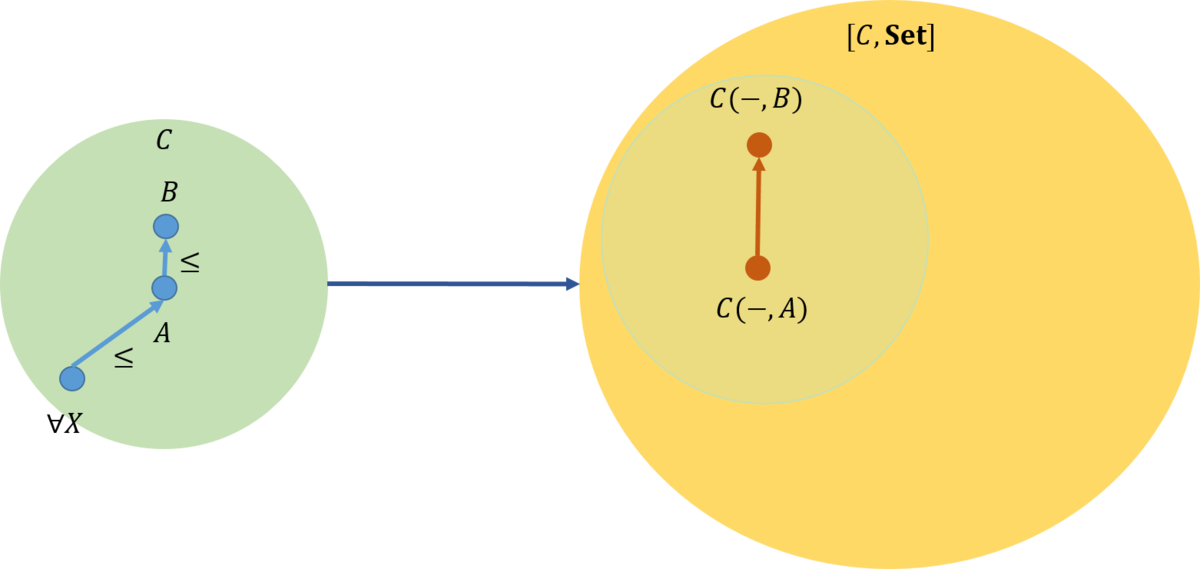
このように、米田の補題、あるいは、余米田の補題は証明の助けにもなる。
次回は、圏論の中心である随伴関手を説明しよう。