随伴関手 － 随伴関手をHaskellで表現する

７．８　随伴関手をHaskellで表現する

随分と時間がかかったが、随伴関手をHaskellで表現するための準備がほぼ出そろった。ほぼといったのは、もう一つだけ、頭の体操をしておかなければならないことがある。それは、右随伴関手が表現可能関手でもあるということだ。

１）右随伴関手は表現可能関手である

表現可能関手を復習しておこう。局所的に小さな圏\(\mathcal{C}\)と集合の圏\(\mathbf{Set}\)において、\({\rm Hom}\)関手\(\mathcal{C}(A,-)\)と関手\(F\)の自然変換が、自然同型である時、即ち、
\begin{eqnarray}
\mathcal{C}(A,-) \cong F
\end{eqnarray}
ならば、\(F\)を表現可能関手という。

それでは、右随伴関手が表現可能関手であることを示そう。随伴の定義は次のようになっていた。

\(\fbox {随伴の定義２：}\)
二つの局所的に小さな圏\(\mathcal{C},\mathcal{D}\)において、関手の対\(R: \mathcal{C} \rightarrow \mathcal{D}, L: \mathcal{D} \rightarrow \mathcal{C}\)が次の条件を満たす時、随伴であるという。
\begin{eqnarray}
\mathcal{C} (L(Y),X) \cong \mathcal{D} (Y,R(X)) \\
\end{eqnarray}

これを図で示すと以下のようになることも示した。

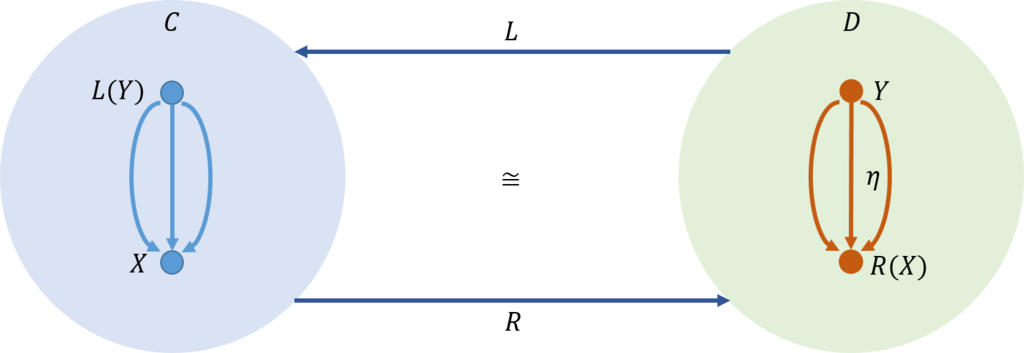
そこで、\(\mathcal{D}\)は集合の圏でもあるので、これを\(\mathbf{Set}\)で、\(Y\)を単集合(singleton setに置き換えると下図を得る。

従って、
\begin{eqnarray}
\mathcal{C} (L( ),X) \cong \mathcal{D} ( ( ),R(X))
\end{eqnarray}
を得る。右側の\(\mathcal{D} ( ( ),R(X))\)は、単集合を\(R(X)\)に写すものである。関数の数は、その集合の要素の数と同じになる。従って、各\(x \in X\)に対して、一つの関数を与えるので、\(R\)は表現可能関手となる。即ち、
\begin{eqnarray}
\mathcal{C} (L( ),-) \cong R
\end{eqnarray}
である。

２）Haskellで表現する

それではすべての材料がそろったので、Haskellで表すことにしよう。ここでは、最初に定義したものを実装することとしよう。定義は次のようになっていた。
\(\fbox {随伴の定義１：}\)
二つの局所的に小さな圏\(\mathcal{C},\mathcal{D}\)において、関手の対\(R: \mathcal{C} \rightarrow \mathcal{D}, L: \mathcal{D} \rightarrow \mathcal{C}\)が三角恒等式を満たす次の射\(ϵ,η\)を有する時、随伴であるという。

\begin{eqnarray}
ϵ : L \circ R \rightarrow I_\mathcal{C} \\
η : I_\mathcal{D} \rightarrow R \circ L
\end{eqnarray}

そこで、\(L,R\)を\(f,u\)とし、\(ϵ,η\)を\(counit,unit\)とすると、次のようになる。

{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE TypeFamilies #-}

class (Functor f, Representable u) => Adjunction f u where
  unit :: a -> u (f a)
  counit :: f (u a) -> a

class Representable f where
  type Rep f :: *
  tabulate :: (Rep f -> x) -> f x
  index :: f x -> Rep f -> x

\(\fbox {随伴の定義 2：}\)
また、定義2に従うと、次のようになる。

{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE TypeFamilies #-}

class (Functor f, Representable u) => Adjunction f u where
  leftAdjunct :: (f a -> b) -> a - u b
  rightAdjunct :: (a -> u b) -> f a - b

class Representable f where
  type Rep f :: *
  tabulate :: (Rep f -> x) -> f x
  index :: f x -> Rep f -> x

定義1と定義2のいずれかが満たされればよいが、両方を一緒に含めても構わないので、この場合には次のようになる。

{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE TypeFamilies #-}

class (Functor f, Representable u) => Adjunction f u where
  unit :: a -> u (f a)
  counit :: f (u a) -> a
  leftAdjunct :: (f a -> b) -> a - u b
  rightAdjunct :: (a -> u b) -> f a - b

class Representable f where
  type Rep f :: *
  tabulate :: (Rep f -> x) -> f x
  index :: f x -> Rep f -> x

なお、三角恒等式は次の条件となる。

  rightAdjunct unit = id
  leftAdjunct counit = id