8.6 モノイドとしての随伴関手
随伴関手の応用についていくつか説明してきたが、アダルトとベビーの例を始めとしてこれまでの例ではすべて、左側の圏の方が厳密であることに気がついただろう。今回の例も同じである。左側がモノイドを対象にした圏、右側が集合を対象にした圏である。
1)モノイド圏と忘却関数
モノイドは加算や乗算などの二項演算を表すのに都合のよい圏である。モノイドであることの条件は、
1) 対象は一つしかない(通常、これは星印で表す)、
2) 射は、通常の写像を連想すると納得するのが難しいが、集合上の要素である、
3) どの射のソースもターゲットも全て同じで、星印である、
4) 射と射の合成は用意されていて、二項演算子が用いられる、
5) 恒等射が用意されている、
もちろん単位律と結合律が成り立っている、というである。
今、モノイドを対象とした圏\(\mathbf{Mon}\)を考えることにしよう。この圏はモノイド\(M,M’\)を対象にしていたとしよう。このとき、\(M\)から\(M’\)への\({\rm Hom}\)集合を\(\mathbf{Mon}(M,M’)\)としよう。
モノイド圏とは別に集合の圏\(\mathbf{Set}\)を用意しよう。また、\(M,M’\)の射は集合の要素であるので、この集合だけを取り出して\(\mathbf{Set}\)に写像する関手\(U\)を考えよう。この関手はモノイドとしての構造を忘れ、射の構成要素だけを取り出すので、忘却関数と呼ばれる。図で示すと次のようになる。

\(U(M)\)と\(U(M’)\)の間にも\({\rm Hom}\)集合\(\mathbf{Set}(U(M),U(M’))\)を考えることができる。
ところで、\(\mathbf{Mon}(M,M’)\)を構成する射のそれぞれは、\(M,M’\)の射を\(U(M),U(M’)\)の集合の要素が同じものを表していると考えるとすると、\(\mathbf{Set}(U(M),U(M’))\)に対応づけることができる。これが、図で実戦で示したものである。その他にも、\(\mathbf{Set}(U(M),U(M’))\)には、\(\mathbf{Mon}(M,M’)\)に対応付けることができない多くのものを含んでいる。これは、\(\mathbf{Mon}\)での\({\rm Hom}\)集合が、\(M\)の構造を維持しなければならないことによる。それに対して、\(\mathbf{Set}\)での\({\rm Hom}\)集合は構造を持たないので、よりたくさんのもので構成されることとなる。即ち、\(U(M)\)の要素数を\(m\)、\(U(M’)\)の要素数を\(n\)とすれば、\({\rm Hom}\)集合の要素数は\(n^m\)となる。
具体的な例を用いて理解を深めることとしよう。下図において、\(M\)は乗算のモノイド、\(M\)はモジュロ3での乗算のモノイドである。

この図で、乗算モノイドの射は、\(M=\{1,2,3,4,5,6,7,…\}\)である。また、モジュロ3での乗算モノイドの射は、\(M’=\{1,2,3\}\)である。この間の射は一つだけで、\(Mod3\)である。\(3\)で割った時の余りを求める関数である。但し、割り切れたときは\(0\)ではなく\(3\)とする。
それぞれのモノイドの射は忘却関数\(U\)によって、\(U(M)=\{1,2,3,4,5,6,7,…\}\)と\(U(M’)=\{1,2,3\}\)に写す。\(U(M)\)から\(U(M’)\)への\({\rm Hom}\)集合には、\(Mod3\)に対応するものが一つ存在することは自明である。そして、\({\rm Hom}\)集合にはこれ以外にもたくさんあることも自明である。
2)自由モノイド
さてモノイドの性質が分かってきたところで、随伴関手との関係を調べることにしよう。右側の関手として忘却関手を用いることにしよう。また、左側の関手として自由関手を用いてみよう。生成された集合の要素の全てにたして、異なる射を与えられるというのが自由関手だ。
加算の場合
まず、例から見ていこう。生成元が\(1\)だけである集合を考えよう。これは、任意の数だけ\(1\)を並べたものが集合の要素となるので、これから作られる集合は\(X=\{\phi,1,(1,1),(1,1,1),…\}\)となる。これを射の集合としたものが自由モノイドである。合成を加算としよう。これで、加算モノイドが得られた。これから、モジュロ3の加算モノイドを作ることを考えよう。さらに、これを忘却関数で\(\mathbf{Set}\)に写すと下図が得られる。

この図で、二つの圏が自然同型であるとしよう。今、\(\mathbf{Mon}(F(X).M)\)にはただ一つの関数\(h=Mod3\)が存在するので、\(\mathbf{Set}(X,U(X))\)でも一つの関数が存在することとなる。これを\(f\)としよう。
これを縦と横をひっくり返すと下図のようになる。
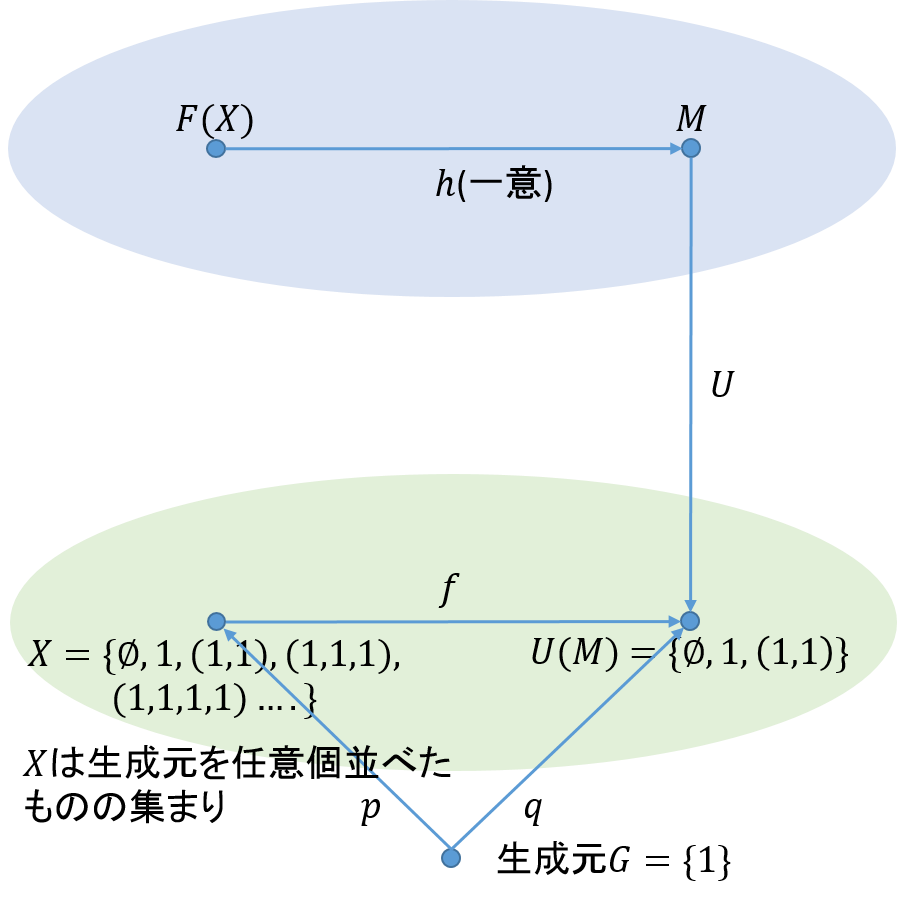
自由モノイドの定義
自由モノイドは次のように定義される。生成元\(G\)から関数\(p\)によって生成された集合\(X\)に対して、その要素を射とするモノイド\(F(X)\)を生成する。これとは別に任意のモノイドを選んできたとする。これを\(M\)としよう。\(F(X)\)から\(M\)への関数\(h\)が一意的に与えられ、\(M\)から忘却関手\(U\)によって得られた\(U(M)\)に対して\(X\)からの関数\(f: X \rightarrow U(M)\)が存在するとき\(F(X)\)は自由モナイドと呼ばれる。なお、\(U(M)\)は生成元\(G\)より関数\(q\)によって生成されたものとする。
今回の例では、\(M\)としてモジュロ3の加算モノイドを用いたが、これが任意のモノイドについていえれば、加算モノイドは自由モノイドとなる。実は、この証明はそれほど難しくはないので、試みて欲しい。
乗算の場合
乗算での生成元は何を考えたらよいのだろうか。中学の頃、素因数分解というのを習った。数を素数の積で表すものだ。全ての数は素数の積で表すことができるので、乗算での自由モノイドを求めるためには、素因数を用いるとよい。そこで下図のようにした。

\(X\)は重複を許して素数を任意に並べたものの集まりである。即ち、
\begin{eqnarray}
X &=& \{\phi,2,3,(2,2),5,(2,3),(3,2), \\
&& 7,(2,2,2),(3,3),(2,5),(5,2),11,\\
&& (2,2,3),(2,3,2),(3,2,2),13, \\
&& (2,7),(7,2),(3,5),(5,3),(2,2,2,2),…\}
\end{eqnarray}
である。
自由モノイドは、\(\phi\)を恒等射とし、他を射とし、合成を\(\circ\)としたものである。即ち、
\begin{eqnarray}
F(X) &=& \{1,2,3,2 \circ 2,5,2 \circ 3,3\circ 2, \\
&& 7,(2 \circ 2 \circ 2),3 \circ 3,2 \circ 5,5 \circ 2,11,\\
&& 2 \circ 2 \circ 3,2 \circ 3 \circ 2,3 \circ 2 \circ 2,13, \\
&& 2 \circ 7,7 \circ 2,3 \circ 5,5 \circ 3,2 \circ 2 \circ 2 \circ 2,…\}
\end{eqnarray}
また、乗算モノイド\(M\)も用意した。自由モノイドから乗算モノイドへは一意的な関数\(h\)が存在し、単射ではないことに注意しよう。即ち、自由モノイドでは異なる射と思われていたものが自由モノイドでは同じ射へと移されている。例えば、自由モノイドでは\(2 \circ 3\)と\(3 \circ 2\)は異なるものとして扱われているが、乗算もなどでは、\(2 \times 3\)と\(3 \times 2\)は同じものである。
もし、二つの圏が自然同型であれば、\(X\)から\(U(M)\)への関数が一つ存在することとなる。最初から、自由モノイドという言葉を用いていたが、乗算モノイド以外の他のモノイドについても同じことがいえるので、これは文字通り自由モノイドであることが分かる。その証明は以下の図を参考に試みて欲しい。
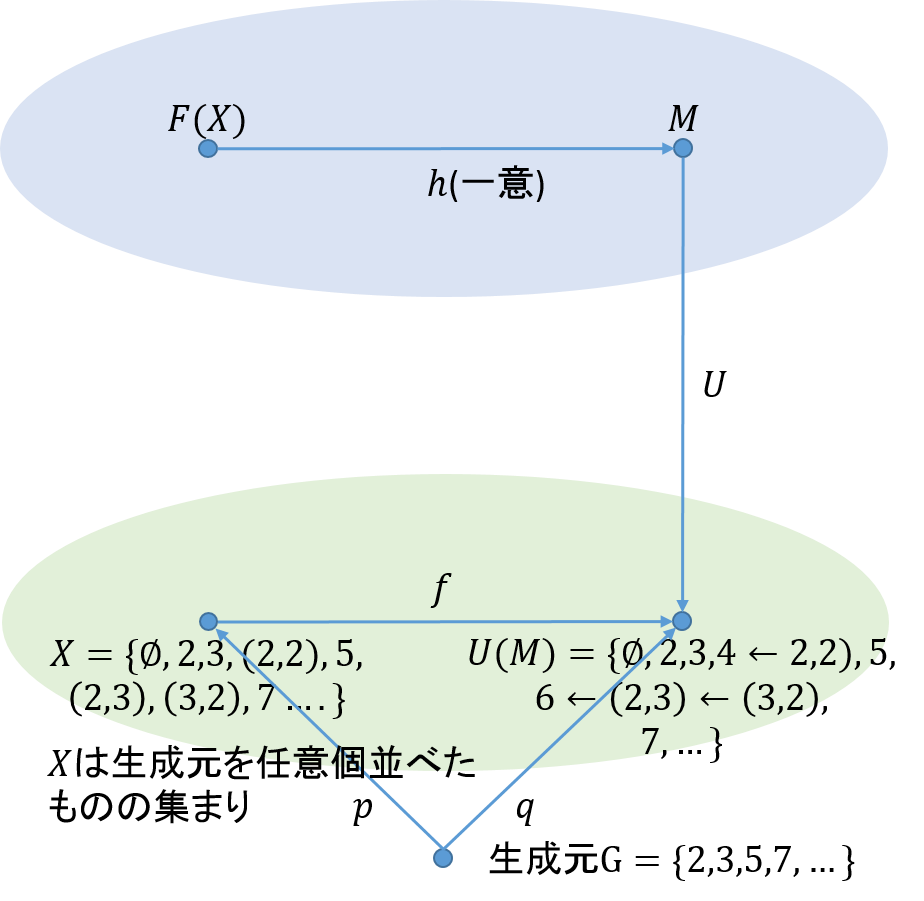
まとめ
今回は、加算と乗算を取って、自由モノイドの説明をしたが、この議論は一般的に行うことが可能である。手順は次の通りである。
1) 生成元\(G\)を用意する。
2) \(G\)の要素を任意個並べたものを漏れなく用意する。これを\(X\)(圏\(\mathbf{Set}\)の対象)とする。このときの関数は\(p: G \rightarrow X\)である。
3) 自由関手\(F\)を用いて、\(X\)を射の集まりとしたモノイド\(F(X)\)(圏\(\mathbf{Mon}\)の対象)を作成する。
4)任意のモノイド\(M\)(圏\(\mathbf{Set}\)の対象)を選ぶ。そして、\(X\)から\(M\)には一意的な関数\(h\)があることを確認する。
5) 忘却関手\(U\)を用いて、集合\(U(M)\)(圏\(\mathbf{Set}\)の対象)\)を作成する。生成元\(G\)から\(U(M)\)への関数\(q\)が存在することを確認する。
6) 関数\(f : X \rightarrow U(M)\)が存在することを確認する。
これで自然同型となり、\(F(X)\)は自由モノイドであることが保証される。
最後にまとめることとしよう。
\(\fbox{随伴関手と自由モノイド}\)
集合の圏\(\mathbf{Set}\)とモノイドの圏\(\mathbf{Mon}\)において、自由関手\(F :\mathbf{Set} \rightarrow \mathbf{Mon}\)が左随伴関手であり、忘却関手\(U :\mathbf{Mon} \rightarrow \mathbf{Set}\)が右随伴関手であるとき、下図で、\(F(X)\)は自由モノイドとなる。なお、\(X\)は\(\mathbf{Set}\)全体となる。これは証明して欲しい。

逆に、\(F(X)\)が自由モノイドの時、下図で、上の部分をモノイドの圏\(\mathbf{Mon}\)とし、下の部分を集合の圏\(\mathbf{Set}\)としたとき、自由関手\(F\)は左随伴関手となり、忘却関数\(U\)は右随伴関手となる。
