1.6 自然変換
対象の間をつないだものが射、圏の間をつないだものが関手、そして関手の間をつないだものが自然変換である。射での合成は、関手でも保存されたが、自然変換でも同じように保存される。
関手は二つの圏を結ぶものであった。このため一方の圏は関手のドメインとなり、他方の圏は関手のコドメインであるが、本当の意味でドメインになるのは一方の圏の対象であり、コドメインとなるのは他方の圏の対象である。
従って一方の圏から対象\(X\)を任意に選んだとき、関手\(F,G\)のドメインは\(X\)で、コドメインはそれぞれ\(F((X),G(X)\)である。関手\(F,G\)をつなぐ自然変換\(α\)はドメインごとに定義され、ドメインは自然変換\(α\)の成分と呼ばれる。従って成分\(X\)に対しての自然変換は、\(α_X:F(X) \rightarrow G(X) \)で定義される。
圏\(\mathcal{C}\)で任意の射\(f:X \rightarrow Y\)を考える。このとき、対象\(Y\)を成分にして、自然変換\(α_Y:F(Y) \rightarrow G(Y) \)を定義することができる。このとき、それぞれの関係は図28に示すようになる。
それでは、自然変換をストリング・ダイアグラムで表すこととしよう。例によって、圏\(1\)を用意し、\(\mathcal{C}\)の対象と射を、それぞれ関手と自然変換に変えよう。これは図29になる。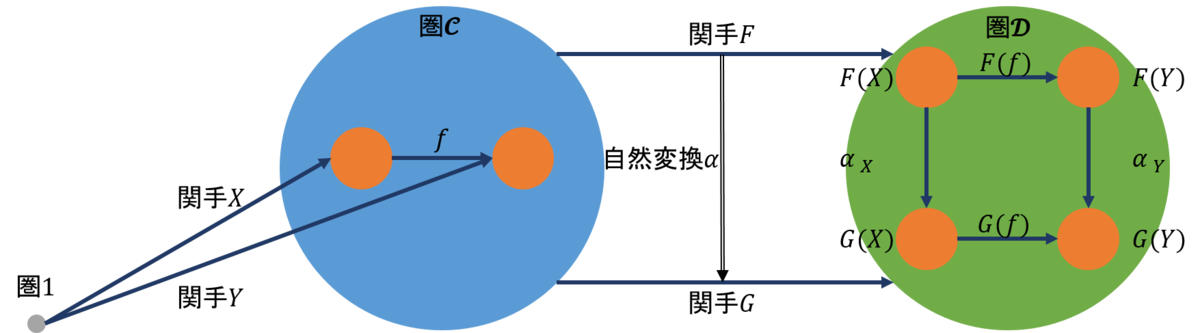
図30はこれのpasting diagramである。
ストリング・ダイアグラムでは複数の表現方法が可能であるが、その代表的なものが図31である。この図で右側の2つのダイアグラムが、自然変換の定義に相当する。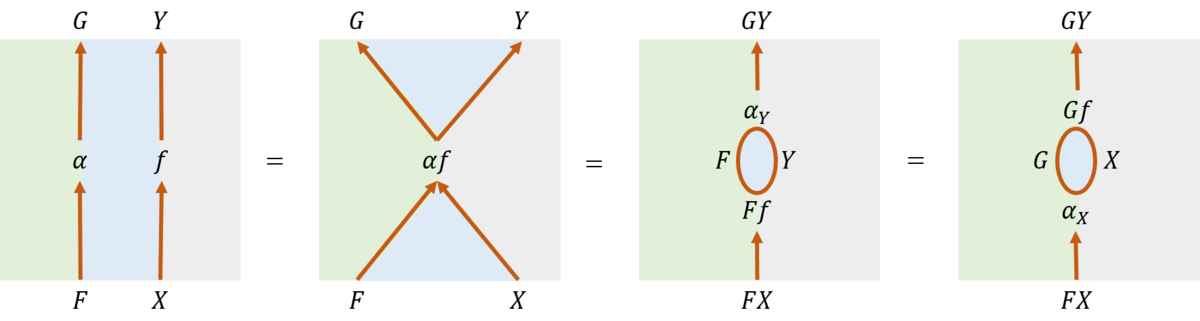
用語説明:自然同型
自然変換は射の一種である。このため同型射を考えることができる。同型射は、ドメインからコドメインへの射が全単射であることを言う。これと同じように、自然同型とは、任意の成分\(X\)に対しての自然変換\(α_X:F(X) \rightarrow G(X\)が全単射となっていることである。
あるいは次のように定義することもできる。関手\(F\)から関手\(G\)への自然変換\(α_X\)が自然同型であるとは、任意の成分\(X\)に対して、\(β_X \circ α_X = I_F\) かつ\(α_X \circ β_X=I_G\) となるような、関手\(G\)から関手\(F\)への自然変換\(β_X\)が存在するときである。これを図で示したのが付録7である。
自然同型をストリング・ダイアグラムで表すと次のようになる。なお、\(u \in F(X), v \in G(X) \)である。