横浜市農村生活館みその公園『横溝屋敷』を訪れる

家にこもっての読書にもさすがに飽きてきて、毎日の散歩で行く場所よりも離れたところに行きたいという衝動にかられ、横浜市鶴見区にある古民家を訪ねてみた。東横線大倉山駅から歩いて25分の距離だが、コロナの流行が下火になったとは言えないこの時期に、電車は避けたいと躊躇し自家用車でとした。

あらかじめパソコンで調べると、この春に開通した横浜北西線を利用すれば40分弱の場所であった。カーナビに目的地をセットして走り出したところ、16号線のバイパスを利用するようにと指示された。ここは首都圏でも最も渋滞する道として知られているところなのになぜと怪訝し、逆らってパソコンが教えてくれた北西線の入り口である青葉インターチェンジを目指して、国道246号線を東京方面に向かった。

おかしなことにカーナビは青葉インターチェンジに近づいても高速道路に乗るようには指示してこなかった。奇妙だとは思ったが、初志貫徹で高速道路に入ると、カーナビから道が消えた。新しくできた道路なのでカーナビの方が対応できていなかったのである。

新横浜を通り過ぎて横浜北線に入ったところからカーナビは再び活動を始め、岸谷生麦で降りるようにと指示してきた。行き過ぎではと思っていると、馬場という出口表示が高速道路に現れた。ここだろうと思ったが、カーナビにこの出口は表れない。仕方がないので通り過ぎて、カーナビの指定通りに岸谷生麦で降りたが、やはりかなりの回り道となってしまった。

あとで判明したのだが、馬場の出入口もこの春設置されたため、カーナビは対応していないことが判明した。出発前に分かっていれば、スマホの地図案内を利用したのにと思った次第である(ちなみにアメリカでレンタカーを利用するとカーナビはついていない。多くの人がスマホの地図案内を利用するためである)。

回り道をしたがそれでも1時間足らずで目的地の「みその公園『横溝屋敷』」に到着した。横溝屋敷は、幕末から明治時代中期に建てられた、江戸時代農村の原風景を残す建物群である。横溝家は、16世紀末の慶長年間から獅子ヶ谷村の名主を務め、代々五郎兵衛と名乗った。今昔マップで明治39年の土地利用を見ると、鶴見川に沿って水田が開けていることが分かる。横溝家は、図中の赤丸の位置にあり、谷戸への入り口に面していて、公園の名称ともなっている御園(みその)と呼ばれた一等地に住んでいたそうである。

国立歴史民俗博物館のデータベース「旧高旧領取調帳」で調べると、獅子ヶ谷村の旧領名は久志本左京(110.8石)、小田切愛之助(199.1石)となっているので、この村は2名の旗本による相給であったことが分かる(この取調帳は幕末期頃の村落の実体を示す)。

また新編武蔵風土記稿は獅子ヶ谷村を紹介し、最後に「旧跡小田切屋敷跡」に触れている。そこには、慶長年間まで小田切美作守が久しくここに住んでいたが、江戸に召し出され、ここを知行地とした後、現在の里正(五郎兵衛)の先祖に一部を与えたと記されている。現在の横溝屋敷の場所が小田切屋敷跡という保証はないが、もしそうだとすれば屋敷の後ろの小高い丘は殿山となる。


ちなみにこの村の人口は、文政10年(1827)38軒226人、安政2年(1855)39軒224人、明治3年(1871)42軒278人と推移した(今年1月の人口は7191人)。石高は正保年間(1645-48)244石余り、天保・明治元年(1831-69)309石であった。

それでは横溝屋敷に入ってみよう。最初は屋敷への入り口となる長屋門である。背景に小高い山があり、緑に囲われた旧家であることを伝えてくれた。

長屋門をくぐり抜けると、正面にどっしりと構えた主屋が現れた。先日の薬師池公園の永井家と比較すると、とても大きい。

その横には蚕小屋が並んでいた。明治の初めごろにこの地方でも養蚕が盛んだったことを伺わせてくれる。

主屋の中は、部屋は広々とし、柱は太く、明るい。住み心地は良さそうに思えた。


主屋と蚕小屋

外に出ると竹林、またこの時期は紫陽花が美しい。

主屋の2階は養蚕に使われていたそうだが、今は展示室となっている。一生懸命に勉強したのだろうか、論語の本の横に和算の本が並んでおかれていた。

この家の住人が書いたのであろうか、屋敷の風景画も、

さらには家の模型も、

2階から眺めた長屋門、

半夏生(はんげしょう)だろうか、庭先にあまり見かけない花を見かけた。

買い物をする都合もあり帰路は一般道を利用したが、幸いなことに新設の道路はなく、カーナビは役に立ってくれたが、カーナビの地図更新もすでに有料になっているので、どうしたものかと思い悩んでいるところである。

日本の歴史公園100選に選ばれた薬師池公園を訪れる

中先代の乱の古戦場「井手の沢」のあとに訪れたのは薬師池公園、2007年には「日本の歴史公園100選」にも選ばれた町田市を代表する公園で、季節に応じて、梅、椿、桜、花菖蒲、古代ハス、紅葉などを楽しむことができる。いまの時期は花菖蒲と紫陽花である。

公園の名称にもなっている薬師池はかつては「福王寺池」と呼ばれたそうで、この池は戦国時代に農業用の溜池として開発された。この地域の支配者であった北条氏照が、天正5年(1577)に、野津田の武藤半六郎(河井家祖先)に印判状を下し、天正18年に溜池は完成した。

北条氏照は、後北条家3代目氏康の子で、4代目氏政とは同母兄弟である。氏照は大石家に養子に入って大石源蔵氏照と名乗り、滝山城主となる(1563~67の間に)。武田信玄との戦い(1569年)で敗れたのち北条に復姓する。父の氏康が死去(1571年)、遺言に従い兄の氏政が、上杉との同盟を見限り武田と同盟を結んだため、今度は上杉謙信と戦うことになる。謙信没後(1678年)に上杉家では家督争いが生じ、紆余曲折の末、上杉と武田が和睦し、氏政は武田との同盟を破棄する(このときは勝頼、信玄は1573年に死去)。武田勢からの攻撃に備えて、氏照は八王子城を構築し(1581年)、のちに移る。豊臣秀吉の小田原攻め(1590年)のとき、小田原城に駆けつけ籠城し戦うが敗北、自刃した。

氏照の略歴からも分かるように、薬師寺池が開発されたのは、戦いに明け暮れていた時期で、領主も百姓も溜池の開発どころではないように思える。その理由を知りたいところだが、公園の案内にはない。ほかにも調べてみたのだが、開発の経緯に関わる資料を見つけることができなかった。その代わりと言っては何だが、どのようなところを開発しようとしたのかを知りたくて、埼玉大学教育学部谷謙二さんの「今昔マップon the web」で調べてみると、明治39年(1906)には下図のようになっていた。

上部(北)が鶴見川、中央のやや下の窪んだところが薬師池である。拡大したのが下図である。薬師池から北の鶴見川に向かって、細く長い谷戸が形成されていて、それに沿って水田が開かれているのが分かる。池から鶴見川まではおよそ1㎞ほど、谷戸の幅はあまり広くはない。ここからの収穫量がどれだけあったのかが気になるが、農業用水確保のための開発に見合うだけの利益はあったのであろう。

薬師池は、宝永4年(1707)の富士山の噴火により泥砂で埋まり3年かけて除去、また文化14年(1817)にも埋まったため掘り直したそうだ。昭和51年(1976)に薬師池公園として開園した。

現在の薬師池公園は下図のように、薬師池を中心に大きな公園になっている。2ヶ月前の4月17日には、薬師池公園四季彩の杜西園(地図では薬師池公園の下の方になる)がオープンしたが、コロナウイルスの影響を受けて、その催しはひっそりと行われたそうである。

我々はオープンしたばかりの西園から入場し、薬師池公園へと向かった。尾根道を越えてしばらく行くと展望が開け、紫陽花や花菖蒲が見事に咲いていた。




公園の中には水車も、

趣のある薬師池、

重要文化財の旧永井家住宅。多摩ニュータウンの建設に伴って、町田市小野路より移築された。建築年代ははっきりしないものの、1600年代末ごろのものと考えられている。建物の幅15m、奥行き8.8m、寄棟造、茅葺で、窓や出入り口が少なく、薄暗い閉鎖的な建物である。

内部に入ってみる。敷居をくぐると大きな土間がある。典型的な農家だと思ったのもつかの間、ヒロマが竹の床なのを見て一瞬たじろいだ。この上にむしろを敷いて利用するのだろう、何とも居づらそうな空間で嫌だと感じた(後で分かったが、竹簾子床(たけすのこゆか)と呼ばれる)。これも後で分かったことだが、この他にヘヤとデイと呼ばれる小さな部屋があり、ヘヤは竹の床、デイは板敷きだそうだ。この家のような間取りは、「広間型三間取り」と呼ばれ、居間(ヒロマ)、寝間(ヘヤ)、客間(デイ)の３間で構成されている。

野津田薬師と呼ばれている薬師堂。天平年間(729~749)行基の開基と伝えられ、現存する薬師堂は明治16年(1883)に再建されたものである。

もう一軒の古民家、江戸時代末期に医院兼住宅として建てられた旧荻野家住宅。木立に囲まれた武蔵野らしい風景で、気に入った。

最後は少し急ぎ足になったが、思いもかけず、この時期の美しい花々を見ることができ、充実した一日となった。季節を変えてまた訪れたいと思っている。

中先代の乱の戦場「井手の沢(菅原神社)」を訪ねる

東京都のコロナウイルス感染者は特定の場所に限定されているようであり、都下のはずれに感染者がいるはずもないと考え、空っとよく晴上がった17日に、近くの歴史遺跡を訪れた。

その場所は、町田市の菅原神社。この場所は、鎌倉幕府が終わり、建武の新政が成った翌年の1335年に、鎌倉幕府の復活を目指した北条時行が戦をしたところである。この戦いを含め、時行が鎌倉を支配するまでの一連の戦いは、中先代の乱と称せられる。鎌倉を支配した先代(北条氏)と後代(足利氏)との間にあって、わずかな時期ではあるが(20日間)支配したことからこのように呼ばれる。

北条氏が滅亡したあと、鎌倉幕府最後の執権高時の遺児の時行は信濃に潜伏したが、御内人(みうちびと)の諏訪頼重によって擁立され、鎌倉を目指した。武蔵国に入って、女影原で渋川義季・若松経家を、小手指ヶ原で今川範満を、武蔵府中で小山秀朝を打ち破り、現在は菅原神社となっている「井手の沢(井出の沢とも書かれる)」で足利直義(ただよし)と決戦に臨んだ。下図には、時行がたどったであろう、女影原(図では霞野神社)から井手の沢(菅原神社)を経て鎌倉へ至る鎌倉街道上道を示す。

この当時、鎌倉には後醍醐天皇の皇子成良(なりよし)親王を長に直義を執権とする鎌倉将軍府が設置されていた。時行は、井手の沢に出陣してきた直義を破り、直義は、成良親王や尊氏の嫡子の義詮(よしあきら)らと鎌倉を落ちた(このとき幽閉されていた護良親王は殺害される)。時行は鎌倉に入り、短期間ながら支配した。

この後、尊氏は後醍醐天皇から征夷大将軍の号を与えられなかったにもかかわらず出陣し、直義と合流して勢力を盛り返し、時行を鎌倉より追い出した(その後の時行は、後醍醐天皇から赦免され南朝方の武将として戦っている)。

井手の沢にはいまでは菅原神社が建っている。この神社は鎌倉街道に面し、その裏手に井手の沢の碑があり、背面には由緒書きが残されていた。


新しい説明書きもあった。

その周辺はちょっとした木立となっていた。

鎌倉期の歌謡、宴曲抄「善光寺修行」には、井手の沢について、「かれいい(乾飯)食うべしいにしえも、かかりし井手の沢辺かとよ、小山田の里に来にけらし」と詠まれている。きれいな水が湧きだし、弁当の干し飯を食べるのに都合のよい場所であったようだ。いまでも水が湧いているのだろう、御神水の碑があった。

菅原神社の由緒は以下の通り。

室町時代に大沢左近正次が京都北野天神に詣でたときに得た天神像をこの地に奉安したのが始まりで、江戸時代の初期、その子孫の大沢玄蕃(げんぱ)が新たに天神像を奉安し、享保7年(1722)に本殿が再建、天明5年(1785)に社殿が造られたとのことである。平成24年に竣工した社殿はなかなか立派な建物である。

平成29年に竣功した参集殿、

雅楽などの芸能を神様に奉納する神楽殿、

火伏の神様を祀る愛宕社と狛犬、

最後になったが鳥居。

とてもこじんまりとした歴史散歩ではあったが、久しぶりの外出を楽しむことができ満足した。さらに近くに公園があることを思い出し、今の時期にはあじさいがきれいに咲いているだろうと考えて、立ち寄ってみることにし、古戦場跡を離れた。

チキンライムアフリカ風

またまた手軽に作れるチキン料理の紹介である。前のレシピもそうだったが、今度のレシピの出どころは、堤人美さんの『こんがり焼くだけレシピ』である。この本には、野菜と、野菜・肉あるいは魚介とを組み合わせた料理、いずれもがオーブンあるいはトーストで焼く料理が紹介されている。焼く時間が分かりやすく表題のところに書かれているので、調理時間の目安もつけやすい。その中で、アフリカ風というのが変わっていて面白そうだったので、トライしてみた。

必要な材料はやはりシンプルで、写真のようにこれだけ。鶏もも肉が主である。

鶏肉に味をつけるためにマリネ液を用意した。これには塩(小匙1/2)、胡椒(少々)、ライムのしぼり汁(100ml、2個分)、ニンニクのすりおろし(1かけ)、ハチミツ(大匙2)である。ライムは写真のように1個しか購入しなかったので、冷蔵庫の中にあったレモンで残りの分は代用した。

鶏もも肉(2枚)をマリネ液につけ、冷蔵庫で2時間寝かした。

焼きあがった鶏肉の上に乗せるししとうがらし(6個)を小口切りにした。

アルミホイルを敷き、皮の部分が上に来るようにして鶏肉を並べた。

このような感じに焼きあがった

鶏肉を角皿に移し、その上にししとうがらしを添え、チリパウダーをふった。さらに角皿に残っている焼き汁にナンプラー(大匙1/2)を混ぜた液をさらにかけた。

オーストラリアに滞在した頃、辛みと甘みが混じったタイ料理をよく食し、南国の料理を楽しんだ。今回の料理にも、ハチミツやチリパウダーを用いたので、同じような味なのではと想像していたが、食してみるとと薄味で、それぞれの甘みと辛さがやっと感じられる程度であった。もう少し、味を強くした方が良いようにも感じたが、楽しめる料理であった。

鶏肉のプチ塩釜焼き

コロナウィルスによる自粛が解除される中、外に飛び出す人も増えてきているようだが、もう少し様子を見極めたほうがよさそうに思えるので、家での料理作りをしばらく楽しむことにした。前回は4日もかかる長丁場のラザーニャに挑戦したが、今回は簡単に作れる鶏肉料理にした。

かつて大量の塩の塊で鯛を包んで、蒸焼き料理を作ったことがある。これは塩釜料理と呼ばれるが、あまりにも大量の塩を用いるので、何となく無駄な料理だとその時感じた。今回は、塩の量を節約したプチ塩釜料理を作ることにした。そして鯛ではなく、作るときも食べるときもハンドリングが良い鶏肉を用いることにした。

今回の材料はこれだけである。ラザーニャと比較すると、食材も香味料もとても少ない。

最初に塩釜を作った。全体ではなく、一部を覆うだけのプチ塩釜である。材料は塩(80g)、卵白(1個分)、ローズマリー(1枝)で、ローズマリーは枝からそいで葉の部分だけを用いた。

これらを一緒にし混ぜ合わせた。


アスパラガス(6個)の下端を落とし、下部に切り目を入れた。

角皿にアルミホイルを敷き、オリーブオイルを少し垂らし、手羽元(10個)を並べた。


手羽元に均等になるように塩釜(それぞれ小匙1と少々)をのせた。オーブンを200℃にして15分ほど焼いた。

アスパラガスを角皿に加えて、さらに15分焼いた。その間に食するときに添えるレモンを用意した。

ついでにサラダも。

焼き上がりはこのようになった。鶏肉の上にちょっこと乗っているのが、塩釜。何とも可愛らしく思えた。しかしこれは食べてはいけない。食べる前に外さないと、とてもではないほどの塩辛さを味わうこととなる。

暖かいうちに食したところ、鶏肉に付着したそれほど強くはない塩味とレモンの酸っぱい味が調和し、美味しく頂けた。今回の料理は、手間暇がかからず、短時間で完成するので、時間に追われているときに使うとよいと思った。

プロのレシピでラザーニャ・エミーリア風に挑戦するー仕上げ

4日間かけての調理も、いよいよ最終段階、これまでに作ってきたパスタとソースを使っての仕上げである。ここまでの作業が台無しにならないことを祈りながら、そしてレストランで味わえるような魅力的なディナーとなることを期待して、ラザーニャ・エミーリア風の締めくくりに入った。材料はもちろんこれまでに作ってきたものとパルメザンチーズ、オリーブオイルである。

最初に、ラザニア皿にオリーブオイルをよく塗った。

茹でたことで大きくなり過ぎてしまったパスタを、調理ばさみで整えて、ラザニア皿に敷いた。

その上にミートソースをパスタが見えない程度に薄く敷いた。

さらにペジャメルソースをミートソースが隠れる程度に薄く流し込んだ。

そしてパルメザンチーズをふりかけた。食した後の感想だが、もっとたくさん振りかけて、チーズの味がもう少し出るようにした方が良かったと反省している

さらにパスタを敷いてこの工程を繰り返す。



そして最後のパスタを敷く。

このあと大きなミスを犯してしまった。さらにミートソース、ペジャメルソースを敷いた後、パルメザンチーズを敷くべきなのだが、一番上はパスタで覆われるものと勝手な思い込みをして、これらを飛ばして、いきなりパルメザンチーズをふりかけ、オリーブオイルを軽く散らして、オーブンで焼いてしまった。焼く前の姿、

焼きあがった姿は無残にも、一番上のパスタが焦げていた。

幸いなことに、材料がたくさんあまっていたので、丸い耐熱皿にも、同じ工程で焼く前のラザーニャを用意しておいた。但しチーズを多くしてみようということで、モッツァレラチーズを一番上に加えてあるという違いはあった。

しかしラザニア皿での失敗に気がついて、急遽、この上にソースを加え、さらにモッツァレラチーズをのせて、チーズいっぱいのラザーニャを用意し、同じように、200度のオーブンで1時間ほど焼いた。

この日の食卓を飾ったのは、表面のパスタが焼けてしまったラザーニャであったが、ミートソースとペシャメルソースがうまく溶け合い、内部のパスタのふんわり感と混じりあって、家庭ではなかなか得ることができない、深みのある味で、素晴らしい食卓となり、妻からも好評であった。残念なことに、一番上に置かれたパスタは焦げてしまい、本来のパスタの味を提供してくれなかったものの、焼けたパスタも、歯ごたえがしっかりした美味しいパスタになっていたので、別の料理では使えるのではと予期しない成果が得られた。

また耐熱皿で焼いたラザーニャは後日食べたが、味が染みていて美味しく、チーズたっぷりにしたので、チーズ味も楽しむことができた。

初めての長丁場の料理作りを体験した。手順書を読み違えるミスを何か所かで犯したものの、最後までたどり着くことができ、プロのレシピと料理を楽しむことができた。これで作り方が分かったので、再度挑戦し、お客様にも饗せられるような美味しい味のそして見た目にも美しいラザーニャを作れるようになれればと願っているところである。

プロのレシピでラザーニャ・エミーリア風に挑戦するーベシャメルソース作り

ミートソースに加えてもう一つ用意しておくのが、ベシャメルソース(sauce béchamel)である。材料はこの通り乳製品が多い。ダマにならないように作るのがコツである。

ベシャメルソースは次のようにして作成した。中火で、フライパンにバター(40g)を溶かした。

火力を弱めて(弱火の強め)、薄力粉(40g)を加えペースト状になるまで、焦がさないように注意を払いながら炒めた。黄色の美しいルーになる。

水で濡らした大きな鍋に移し、氷水を入れた大き目のフライパンに乗せて冷やした。

水で濡らした別の鍋に、牛乳(1000ml)とローリエ(1枚)を加え、強火で沸騰する直前まで、温めた。

これを、先ほどのルーが入っている鍋に一気に加え、泡だて器でかき回しながら、ぼこぼこと煮立つまで炊いて、塩と胡椒で味を調えた。

この作業は、ミートソースを煮込んでいるときの待ち時間を利用して行ったが、全く問題なく仕上げることができた。これらの作業は午前中に行ったので、次の組み立て作業は、夕方行うことにし、しばしの休憩を楽しむことにした。

プロのレシピでラザーニャ・エミーリア風に挑戦するーボローニャ風ミートソース作り

ミートソースはこの料理のかなめだ。そのため使う食材の種類も半端ではない。ひき肉を中心に香味野菜、ハーブ、香辛料などがオンパレードだ。

最初に野菜を炒める。材料は玉ねぎ(1個)、にんじん(1本)、セロリ(1本、頂いたレシピは2本の指定だが、購入のときそこまで注意がいかなかったので今回はこれで我慢)、ニンニク(1片、今見ると手順書の方は1/2になっている)、バジリコ(3枚)、干シイタケ(1個、水100mlで戻したもの。浸した水はいらない)。

これをフードプロセッサでみじん切りにした。

大き目のフライパンにオリーブオイルを熱し、みじん切りにした野菜を加え、軽く塩をまぶし、じっくりと炒めた。塩は野菜の水分をとるためだそうだ。手順書には香味野菜から汗をかかせる気持ちで、蒸気を飛ばしながら炒めあげると書かれている。素晴らしく分かりやすい表現に感謝。


バットに取り出すとなっていたが、ないので皿にした。

次はひき肉である。手順書には仔牛または牛の赤身のひき肉(300g)、豚赤身ひき肉(100g)、鶏レバー(30g)とある。しかし私が住んでいる街には、あいにく肉屋さんは存在しない。駅の前にスーパーが一軒だけという完全な住宅街である。隣町の横浜市や大和市へ行けば大きなスーパーがありこれらの食材を得ることも可能なのだが、これらの店は買い物客が多く、テレビのニュースは人込みを避けるようにとも伝えているので、今回は近場で間に合わせることにした、牛のひき肉は300gに少し足りず、豚のひき肉は100gを越えているが、合わせて400gなのでこれで我慢とした。また鶏レバーはなくてもよいということなのでこれは省略した。

野菜を取り出したままのフライパンに、オリーブオイルを熱し、ひき肉を加えた。焼き方は表面を焼き上げるという感じだそうだ。

このまま静かに置いて表面が焼きあがるのを待って、ひっくり返した。ひき肉なので肉が分離し、きれいにひっくり返すことはできない。プロはどうしているのだろうと思ったりもした。ひっくり返した部分の表面に焼き色がついたと思われるころに、ヘラで崩しながら、表面がカリッとするまで、香ばしく焼き上げた。

次の作業は、「香味野菜をフライパンに戻して」となっていたのだが、読み間違えて、新しいフライパンを使ってしまった。
味付けのために用意したのはこれ。炒めた香味野菜と薄力粉(大匙1)、タイム(1枝に相当する程度)、ローリエ(1枚)、ナツメグ(少々)である。

香味野菜をフライパンに戻し、薄力粉をふるい入れ、薄力粉を焼き上げるイメージでしっかりと炒めた。

さらにタイム、ローリエ、ナツメグを加えて、さっと炒めあげた。

次はトマト味をつける。赤ワイン(200ml)、トマトペースト(30g)、トマトホール(400g)を用いる。トマトホールに対して、ヘタと種を取り粗く刻んでおくという注意書きがあった。作業中もこのことは覚えていたのだが、いざとなった時、この部分が見つからず、記憶違いかと悩みながらトマトホールはそのまま加えてしまった。調理中にヘラで切っていけば大丈夫という妻の大胆な発言に救われて作業を続けた。
フライパンにワインを加え、アルコール分を飛ばした。

トマトペーストを加えてしっかりと炒めたあと、トマトホールを加えた。

このとき、肉は何処で入れるのだろうと不安になり、手順書を何度も読み直したり、YouTubeで調べたりして、野菜をフライパンに戻す時だったのではとか、あるいは赤ワインを入れる前だったのではとか思い悩んだが、とにかく、一緒にしようということで、ここで炒めてあったひき肉を加えた。あとになって手順書を読み間違えたことに気がついたのだが、一度思い込んでしまうとなかなか気がつかないものと改めて認識させられた。

ひき肉を混ぜるのが少し遅くなったが、まあ大丈夫だろうと楽観的に考え、赤みが取れてオレンジ色になるまで弱火でじっくりと煮込めという指示に従って作業を再開した。この様子を見ていた妻が、うちの電磁調理器では、いったん中火ぐらいにしてぐつぐつしてから弱火にした方がよいと忠告してくれた。そうかなと思いながらも従った。手順書には、「煮込み料理に液体を入れていくときは、酸味が強いものから酸味の少ない方へ順番に加え、トマトは必ず弱火で」と書かれている。強火で煮込むとトマトの強い酸が出てしまうそうで、妻の忠告が間違いではない範囲の内に収まっていることを願いながら作業を続けた。次の作業に移る前に、このときのトロみを覚えておくようにと手順書には書かれていた。そこでの目標は、このトロみになるまで煮込むことであった。

いよいよ最後の作業だ。フライパンに鶏のだし汁(チキンコンソメ2個と水500mlで作成)を加えて、先ほど覚えたトロみになるまで、塩と胡椒で味を調えながら、じっくり煮込んだ。

前の記事で述べた「説明書を読まない人」には、説明書を読むのが苦手ということが含意されている。今回はこの特性をいかんなく発揮して、見落としや読み違いによるくるいを伴っての調理となったが、味は素晴らしく良かった。少しぐらいの手順の違いを吸収してくれたプロのレシピに感謝して次の工程に進むことにした。

プロのレシピでラザーニャ・エミーリア風に挑戦するー生地作り

昨年暮れ、飯田橋にあるイタリアンレストランで、かつての職場の同僚と、ラザーニャを食した。とても美味しかったのでそのことを告げたところ、ありがたいことに、後日そのレシピを頂くことができた。折角なのですぐに試してみたかったのだが、運の悪いことにコロナウイルスでなるべく外出をしないようにとの自粛が始まり、その影響で家でケーキなどを作る人が増えたのであろう、強力粉や薄力粉が入手できない時期が長く続き、その機会はなかなか訪れなかった。やっと緊急事態宣言が解除され、近くのスーパーの棚にも必要な食材が並ぶようになったので、満を持して挑戦することにした。

挑んだのはプロの手になるレシピ。手順書は3.5ページ、調理にかかる日数も4日だ。うまく作れるか心配だ。常日頃、妻からは説明書を読まない人と言われていて、指示通りに作業することが嫌いあるいはできないタイプであると自身も自覚しているので、これほどの長い指示書に沿って、間違いなくやり通せるかについては自信がない。失敗は次の成功をもたらすだろうと楽観的に考えて、先週の金曜日より、ラザーニャ作りに励んだ。

ラザーニャ(lasagna)は、元々は料理の名前ではなく、平たい板状のパスタのことを言うそうだ（料理の場合には、オーブンで焼き上げたラザニアということで、ラザーニャ・アル・フォルノ(lasagna al forno)とも呼ばれるそうだ）。このため生地を作らないとラザーニャを作ったことにはならない。先だってレモンビスケットの生地を作ったが、今回の難しさはこの比ではない。バリラ社の乾麺を使ってもよいと教わったが、ここは王道を行くことにした。

1日目：生地作り

材料はいたって単純。強力粉(210g)、薄力粉(140g)、玉子(3個)、塩(小匙1/3)、オリーブオイル(大匙1と1/2)だけである。

それでは始めよう。薄力粉、強力粉、塩を用意。

それらを混ぜ合わせる。

ふるいで混ぜ合わせ、ボールに入れる。

真ん中を窪ませ、玉子とオリーブオイルが入る空間を作る。

玉子はかき混ぜる。

さらにオリーブオイルを加える。

これを粉の真ん中に入れる。

周りの土手を崩すようにしながら、水分と粉を馴染ませていく。


水分が全体に回ったところで、生地をひねるようにしてまとめる。


ラップに包んで一晩室内で寝かせる。

2日目：生地伸ばし

午前中の作業をするために、一晩寝かせた生地を取り出す。表面を見ると、水分が多くなり、みずみずしくなったように感じられた。

綿棒でひたすら伸ばす。目標は厚さ0.7ミリ。

さらにさらに伸ばしていく。

長くなりすぎてしまったので、3つに分割（頂いた作業書には分割してよいとは書いてない。正しい方向に進んでいるのかが心配）
さらに伸ばす。

伸びなくなってきたので、ラップに包み、丸い棒に巻いて室内で、夕方まで寝かせる（これによりグルテンの力が弱まるそうだ。グルテンは、穀物の胚乳から生成されるたんぱく質のグルテニンとグリアジンが水を吸収して網目状につながったものである）。


夕方取り出し、再度伸ばして、目標の0.7ミリになったところで、生地の切り分け作業に入る。手順書には、グラタン皿の大きさに合わせて切ると書かれている。これまでは丸い耐熱皿を用いてラザニアを作っていたが、今回のイベントに合わせて、ラザニア皿を購入した。しかし明日届くことになっているので、正確な大きさが分からない。購入先の広告を見ておおよその寸法を得たのだが、合っているか心配である。取り敢えず型紙を作って、それに合わせて、板状のパスタを作成（次の日に茹でるという作業があるのだが、パスタが伸びることを計算に入れてなかった。実はもっと小さめで良かった）。


さらに端切れを利用して、小さいのも作る。

初めてにしてはうまくいったかなと自己満足し、次の作業に備えて涼しいところで一晩寝かせた。

3日目：生地を茹でる

朝になってびっくり。生地は乾いているものの、曲がったり、ひび割れたりしていて、お行儀が悪い。伸ばしたときの厚さが一様でないことが影響したのだろうか、原因は定かではない。

少し気落ちしながらも、茹でる作業にとりかかった。一つ一つ茹でていくので、時間節約のために茹でるための鍋を二つ用意した。それぞれには、7分目ぐらいの高さまで水を入れ、小匙1杯程度のオリーブオイルと大さじ1杯程度の塩を加えた。オリーブオイルはパスタがくっつかないようにするためだそうだ。但し、沸点が高くなるので注意とのことでもあった。また茹で上がったパスタを冷やすための氷水も用意した。

生地は一枚一枚、透明感が感じられるようになるまでゆでた。また浮き上がっても来るので、小さい生地のときはそれを目安としたが、大きい生地の場合には、中心付近では下から上がってくるお湯の流れで常に浮き上がった状態になり判断しにくかったため、生地の色の変化を観察して取り出した。

茹で上がった生地はすぐに冷水に入れて冷やす。

ふきんで水分をとる。

一枚一枚ラップで包む。

型紙と比較すると、随分と膨張していることが分かる。次の作業のときは、さみで切り取って整形して使うことにし、一晩冷蔵庫で寝かせた。

茹でたパスタを食してみたところ、ふんわりとした感じがありとても美味しく感じられ、戦場状態の忙しさであったことも忘れ、明日の完成に向けて希望が湧いてきた。

4日目：いよいよ完成

最後の日、ラザニア皿に並べた。

今回の反省点：➀パスタ一枚一枚の大きさはラザニア皿の大きさでなくてよい。茹でやすさなどを考慮すると、茹で上がった時にラザニア皿の半分程度になるのがよさそうである（今回使用したラザニア皿(直径26.7奥行15.3深さ4㎝に対しては、10cmx5cmのパスタにするのがよさそう）。②生地を伸ばすと、大きく広がり過ぎて作業がしにくくなるが、このときは分割してよい。ラザニア皿には、一枚のパスタでなくても、タイルのように張り詰めも構わない。並べているときは美的な差を感じないわけでもないが、このあとの調理でその差はなくなってしまうので、形はあまり気にせず、同じ厚さになるように注意を払った方が良い。③ただ厚さを一様にするのはかなり難しそうで、一工夫も二工夫も必要そうである。

ということで、さらに次に進むことにしよう。

Ubuntuに搭載の代数幾何学用ソフトMacaulay2を遠隔操作でWindowsマシンより利用する

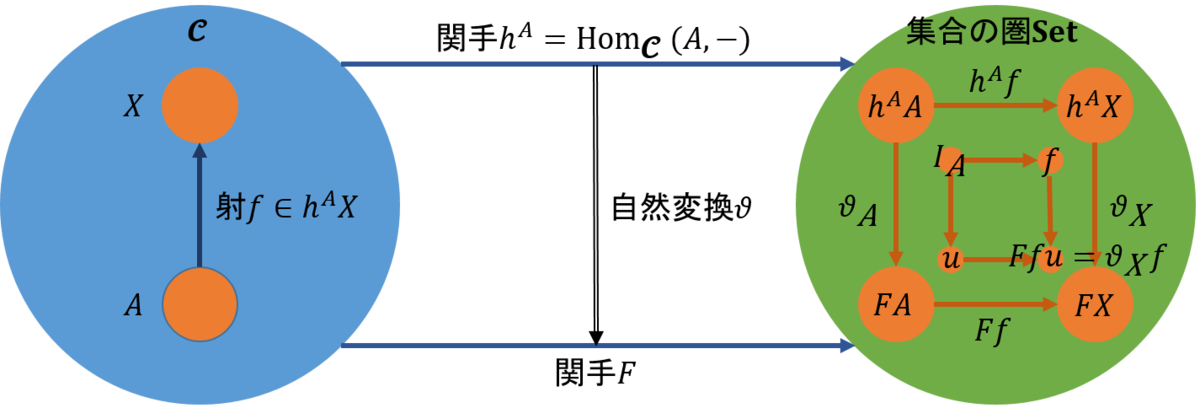
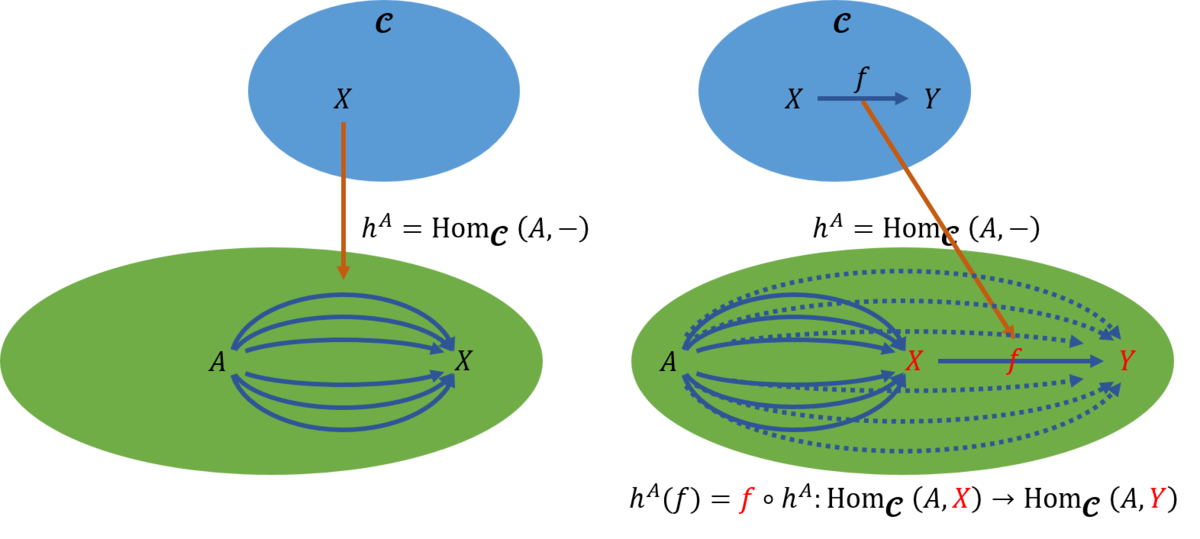
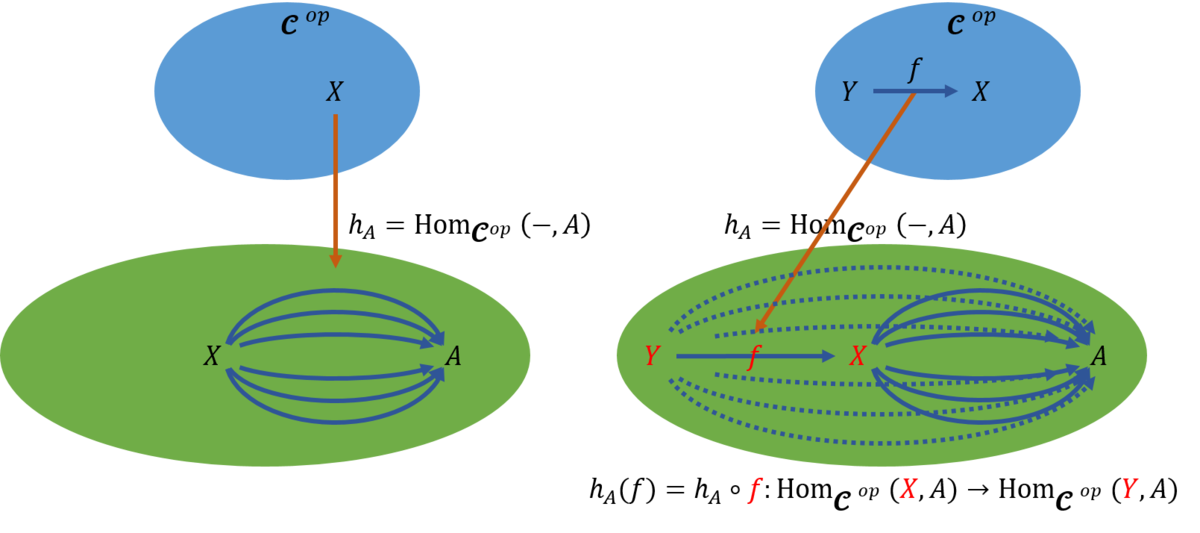
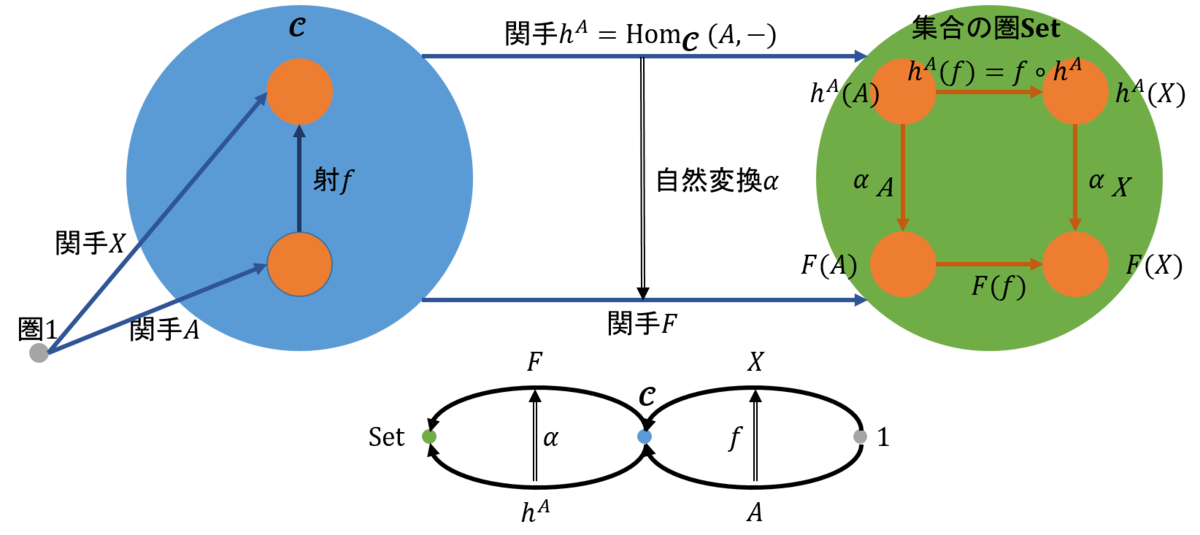
表現可能関手の記事を書いているときに、表現可能という専門用語が代数幾何学からの由来であるらしいことを知り、代数幾何学を少しでも理解しようとして、よさそうな参考資料を探して読んでいるときに、Macaulay2と呼ばれるソフトがあることを知った。これは、代数幾何学(algebraic geometry)と可換環論(commutative algebra)での研究を支援するために開発されたそうである。

1992年からアメリカ国立科学財団(National Science Foundation)の基金を得て開発が始まったとのことなので、どこかで聞いたかもしれないのだが、興味がなかったために見過ごしたものと思われる。代数幾何学の勉強のついでに、Macaulay2について少し調べてみると、グレブナー基底(Gröbner bases)によるアルゴリズムを含んでいるということなので、少し使ってみようと思い立ち、自宅のコンピュータへのインストールを試みた。その時の経験を記しておこう。

Macaulay2はLinuxの環境でしかサポートされていないということだったので、Ubuntuをインストールしてあるが、普段は使っていないコンピュータを利用することにした。これは、元々はwindouws7が搭載されていたデスクトップコンピュータだったが、利用価値がなくなったので、Linux用にと変えたものである。調べてみると、このマシンのバージョンは19.10で、今年5月9日にリリースされた最新のバージョンに簡単にはアップグレードすることができないことが分かった。このマシンにはLatexやHaskellを搭載し何かのときに利用していたので、これらが再実装になることに気後れもしたが、通常リリース(試験的なバージョンといったほうが適切)の19.10ではこれからも困ると思い、最新の長期サポートリリースのUbuntu20.04をインストールすることにした。

インストールそのものはいたって簡単。まずUbuntu Japanese TeamからUbuntu Desktop 20.04LTSをダウンロードしてインストールすればよいはずだったのだが、DVD-RWに書かれていた前のバージョンを消去して焼直したのだが、このとき表面をきれいに掃除するのをさぼったため、正しく書き込まれにくい状態になっていた。さらにさぼって焼いた後の確認作業を省き次の作業に移ったため、インストール中に予想もつかない様々なエラーが発生し、無駄な時間を費やしてしまった。再度焼き直し、インストールを開始したところスムーズに進み、タイムゾーンとユーザ情報の設定などをして使える状態になった。急がば回れの格言通りで、手抜きをしてはいけないと改めて反省した。

そしていよいよMacaulay2のインストールだ。18.04に対しての説明はあちらこちらにあるのだが、20.04についてはなかなか見つからない。リリースされてからあまり日がたっていないので、まだなのかとあきらめかけたころ、イリノイ大学の数学科のサイトにやっと適切な記事を見つけることができた。　
https://faculty.math.illinois.edu/Macaulay2/Downloads/GNU-Linux/Ubuntu/index.html
先ほどの作業ではないが、このホームページもかなり手抜きで、大学のホームページにもかかわらずその背景にある考え方が説明されていない手順書になっていて、なぜこのようなことをしているのかを理解できないまま、指示に沿って操作を進めざるを得なかったことに不満が残った。インストールした後に分かったことだが、要は公開鍵暗号方式を利用して、実行可能なバイナリのプログラムをダウンロードするということであった。このため、私の側には、公開鍵とMacaulay2のプログラム名を用意しておく必要がある。プログラム名は

deb https://faculty.math.illinois.edu/Macaulay2/Repositories/Ubuntu focal main

で、最後のほうにあるfocalは、リリース20.04のコードネームである。この名前はファイル/etc/apt/sources.list内に記憶する必要があるので、エディタのnanoを用いて行った。公開鍵の格納はいくつかの方法が紹介されていたので、今回は次を用いた。

sudo apt-key adv --keyserver hkp://keys.gnupg.net --recv-key CD9C0E09B0C780943A1AD85553F8BD99F40DCB31

Macaulay2のインストールにはSynapticと呼ばれるパッケージマネジャを用いる。Ubunuをインストールした段階では、このパッケージは含まれていなかった。今回はUbuntuソフトウェアセンターを用いて「Synaptic」で検索してインストールした。起動したSynapticの画面で、「再読込」をクリックすると、公開鍵とプログラム名を用いて、Macaulay2をロードできる状態にしてくれる。Synapticの左上にカテゴリーを示す場所があるので、数学にすると、右側にmacaulay2とmacaulay2-commonが現れるので、これにチェックを入れ、「適用」のボタンを押すとインストールされる。インストールされていれば下図のようになる。

これでOKなので、M2と入力すれば使うことができる。

しかし直接では記録も残らないので、emacsから使えるようにした。このため、ホームディレクトリの直下に.emacsファイルを作成し、下記を書き込んだ(プログラムの実行は、emacsと打ち込み、emacsの画面が出てきたらF12のキーを押す)。

;; .emacs file in your home directory
 (load "M2-init")
 ; comment out the following line with an initial semicolon 
 ; if you want to use your f12 key for something else
 ; or change f12 to (for example) f8
 (global-set-key [ f12 ] 'M2)

このようにして準備したマシンだが、残念なことに使い勝手が悪いところに置かれている。そこで通常使っているWindows10のマシンから遠隔操作で利用できるように試みた。やはり18.04に対してはたくさんの説明があるのにもかかわらず、20.04に関してはかなり少ない。18.04ではUbuntu側は画面共有を用いて遠隔操作を実現していたが、同じように20.04で設定してもうまくつながらない。そうこうしているうちに、20.04では繋がらないという記事を見かけたので、別の方法をとることにした。いろいろと試行錯誤の末、VNCを用いることにした。Windows側にはUltraVNCを用いることにし、クライアントとしての利用だけなので、いくつかあるユーティリティの中から、UltraVNC Viewerのみをインストールした。

Ubuntu側にはつぎのようにしてVNCサーバーをインストールした。

sudo apt -y install tigervnc-standalone-server

パスワードの設定も

vncpasswd

VNCに必要なファイルを作成するために、一度起動する。

vncserver :1

そして停止する。

vncserver -kill :1

作成されたファイルに必要な事項を追加する。ここではデスクトップとしてMateを使用することにしたので、/.vnc/xstartupに次の事項を書き込んだ。なおUbuntuをインストールした段階ではMateは用意されていなかったので、ubuntu-mate-disktopをインストールした。

unset DBUS_SESSION_BUS_ADDRESS
exec /usr/bin/mate-session &

これでUbuntu側の準備は完了なので、VNCを起動する。

vncserver :1 -geometry 1280x1024 -localhost no

なお、サーバ側(Ubuntu)のIPアドレスはifconfigで調べられる。

クライアント側ではUltraVNC Viewrを起動する。IPアドレスが要求されるので、アドレスを入れた後にコーロン(:)をつけ、そのあとに１をつけて「connect」ボタンを押す。

パスワードが求められるので、Ubuntu側でのサーバーの設定の時に、vncpasswdで指定したものを入れる。Windows側にUbuntuの画面が現れる(中央右がUbuntuのデスクトップ)。

なお、VNCの安全性を強化するためにSSH(secure shell)接続を行う必要があるが、これはMark Drakeさんのブログ"How to Install and Configure VNC on Ubuntu 20.04"を参照して欲しい。

Windows10からUbuntu20.04に実装されているMacaulay2を利用したのが下記の画面である。多項式\(x^3-y^2\)を代入し、そのイデアルと根基イデアル(グレブナー基底計算を利用)を求めた。この例は、横田博史さんのMacaulay2の紹介(平成22年1月27日)にあるので、詳細はこれを参考にして欲しい。

インストール後の感想である。久しぶりのUbuntuの利用のためインストールに手間取ったものの、使い勝手が良さそうなので、しばらくこれを利用してMacaulay2を楽しもうと思っている。

レモンビスケット

馴染みの店のfacebookでレモンビスケットを見つけた。お店の人がイタリアでの修業時代のレシピを紹介してくれたものだ。巣ごもりが続く中、気晴らしにと挑戦することにした。

簡単そうに見えたのだが、やっと３回目に家族に出しても大丈夫だろうと思われるものが出来上がった。１回目は生地がべとついてしまったので、こねすぎたと考えて途中で断念した。２回目は、同じようにべとべとしていたので、このようなものかと思い、冷蔵庫で１時間ぐらい寝かせてから焼いてみた。味は良かったが、ビスケットのかたちが整わなかったので、勧められるようなものではなかった。そして今回が３回目の挑戦だ。生地を切り分けるときに等量になるように工夫したのだが、予想したようにはうまくいかず、大小の差が生じてしまったが、それでもビスケットらしくなった。

１回目の失敗にはもう一つの理由がある。多くの人が自粛生活を始めるようになった影響で、ケーキを作るのに必要な薄力粉、強力粉、ベーキングパウダーなどが、店頭から消えた。このときもベーキングパウダーがお店になく、使用期限が１年前のものを仕方なく使用したのだが、焼いてみても満足いくようにはうまく膨らまなかった。

それでは作り方を紹介しよう。今回の材料はとてもシンプル。

１）レモン１個の皮をすりおろし、半個のしぼり汁を得る。

２）これに加えてグラニュー糖(50g)、キャノーラ油(50g)を用意。

３）これらをボールに移してよくかき混ぜる。

４）卵(１個)を溶いて、その半分をボールに加え、さらに良くかき混ぜる。トロっとした状態になった。

５）薄力粉(150g)、ベーキングパウダー(小匙１杯)をボールに移し、かき混ぜる。

６）これをふるいに移し、先ほどのレモンのしぼり汁などのボールに、ふるい入れる。

７）３回に分けてふるい入れ、その都度、液と混ぜた。

８）切るようにして生地をこねる。表面がつるっとし、手にべとべとつかなくなるくらいまでこねた。

９）この状態で切り分けようとするとヘラにくっついてくるので、冷蔵庫に１時間ほど寝かせ、生地が落ち着くのを待つ。

１０）生地を４等分し、さらにそれらを９等分して。それぞれを丸くし、粉糖の中に入れる。

１１）真ん中をへこませ、形を整えて、オーブン皿に隙間を作って並べる。

１２）オーブンを１８０℃にして２０分間焼く。

１３）冷ますために網の上にのせる。

生地の切り分けに当たっては、同じ大きさになるように工夫を凝らしたが、やはり大きさでの差が生じてしまった。次回は一つ一つの重さが9g程度になるように測り、均等な大きさになるようにしたいと思っている。ビスケットそのものは、レモンの香りとさわやかな味がマッチしてとても美味しく、一つ食べると止まらなくなるほどである。

最後はおまけである。定番の川に沿っての散歩は、雰囲気が良いので楽しむ人が多く、コロナウイルスのこの時期は避けたほうが良さそうなので、東工大のすずかけ台キャンパスの周囲を歩いているが、そのときに可愛らしいお地蔵さま(寛政：19世紀が始まるころ)と道祖神(昭和25年)を見つけた。この辺りの歴史については詳しくないが、そのうちに調べてみようと思っている。

圏論：ストリング・ダイアグラム ー 米田の補題

４．米田の補題

いよいよ米田の補題の証明である。これは次のようになっている。

局所的に小さい圏\(\mathcal{C}\)(任意の2対象\(A,B\)に対して\({\rm Hom(A,B)}\)の類が集合となっているような圏)について、共変\({\rm Hom}\)関手\(h^A:\mathcal{C} \rightarrow \mathbf{Set}\)から集合値関手\(F:\mathcal{C} \rightarrow \mathbf{Set}\)への自然変換と、集合である対象\(F(A)\)の要素との間には一対一の対応が存在する。即ち、
\begin{eqnarray}
Nat (h^A,F) \cong F(A)
\end{eqnarray}
である。

あるいは、圏\(\mathcal{C}\)と圏\(\mathbf{Set}\)により作られる関手圏を\([\mathcal{C} , \mathbf{Set}]\)で表し、
\begin{eqnarray}
[\mathcal{C} , \mathbf{Set}] (h^A,F) \cong F(A)
\end{eqnarray}
が成り立つというのが米田の補題である。

４．１　証明の準備

それでは証明のための準備をしよう。米田の補題を証明するために図１を用いる。

図１：米田の補題を証明するための説明図

まず、米田の補題に関して射\(φ_{FA}\)を次のように用意する。
\begin{eqnarray}
φ_{F,A}:Nat (h^A,F) \cong F(A)
\end{eqnarray}

射\(φ_{FA}\)を自然変換\(\partial \in Nat(h^A,F) \)に対して、
\begin{eqnarray}
φ_{F,A}\partial=\partial_A I_A
\end{eqnarray}
と定める。
さらに、\(F(A)\)から出発して\(F(X)\)に至る経路は\(h^A(A)\)から\(h^A(X)\)を経由する場合と、直接至る場合とがあり、これらが可換である。そこで、
\begin{eqnarray}
ψ: F(A) \rightarrow Nat (h^A,F)
\end{eqnarray}
を任意の\(u \in F(A) \)に対して、
\begin{eqnarray}
ψ(u)_X (f) &=& F(f)(u) \\
f & : & A \rightarrow X
\end{eqnarray}
と定める。このとき、\(ψ(u)_X= \partial_X \)である。

米田の補題を証明するためには、次の3項目を証明すればよい。
１）\(ψ(u)\)が自然変換である。
２）\(ψ=φ_{F,A}^{-1}\)である。
３）\(F,A\)に対して自然である。

４．２　米田の補題をストリング・ダイアグラムに

米田の補題をストリング・ダイアグラムで表すことにしよう。図２に示すように、例によって圏\(1\)を設け、圏\(\mathcal{C}\)の対象\(A,X\)を、圏\(1\)から\(\mathcal{C}\)への関手として表すことにする。なお図２下はpasting diagramである。

図2：説明図をストリング・ダイアグラムに変えるための準備

準備のところで得た二つの式は図３のストリング・ダイアグラムになる。

図３：\(φ_{F,A}\partial_A I_A\)と\(ψ(u)_X= \partial_X \)をストリング・ダイアグラムで表す。

４．３　米田の補題の証明

それでは順を追って証明していこう。最初の項目から始めよう。
１）\(ψ(u)\)が自然変換である。
\(ψ(u)_X=\partial_X\)であることから、\(\partial: h^A \rightarrow F\)が自然変換であることを言えばよい。即ち、任意の\(X,Y\)に対して、図４が可換になることを示せばよいので、\(h^A(X)\)から出発して\(F(Y)\)に到達する経路において、\(F(X)\)を経由する場合と\(h^A(Y)\)を経由する場合は同値であることを示せばよい。

図４：\(ψ(u)\)が自然変換となるためには、ここでの図式が可換になること。

すなわち、
\begin{eqnarray}
\partial_X & : & h^A (X) \rightarrow F(X) \\
F (g) \partial_X &=& \partial_Y h^A (g)
\end{eqnarray}
が成り立つことを示せばよい。

それではストリング・ダイアグラムを用いて証明してみよう。図5のようになる。これは、\(f:A \rightarrow g\)を利用して、\( F (g) \partial_X f = \partial_Y h^A (g (f ))
\)となることを示している。

図５：\(ψ(u)\)が自然変換であることをストリング・ダイアグラムを用いて証明する。

細部を確認してみよう。図で(1)から(2)は、\(\partial_X\)を\( ψ(u)_X \)で置き換え、さらに\(f \in h^A(X)\)であることを利用。(2)から(3)は、\(ψ(u)_X (f) = F(f)(u)\)を利用。(4)から(5)は、\(ψ(u)_Y (gf) = F(gf)(u), g : X \rightarrow Y\)を利用した。

２）\(ψ=φ_{F,A}^{-1}\)である
証明を図６に示す。(3)から(4)へは、\(ψ(u)_A (I_A) = F(I_A) (u)\)を利用した。

図６：\(ψ=φ_{F,A}^{-1}\)であることをストリング・ダイアグラムを用いて証明する。

３）\(F,A\)に対して自然である。

二つに分け、まず\(A\)に対して自然であることについて考える。

証明に先立って、関手\(h^A\)の性質を復習しておこう。この関手が\(A\)に対して自然であるとき、図７の可換図式を得ることができる。\(f:A \rightarrow B\)のとき、\(h^f : h^B \rightarrow h^A\)と矢印が逆向きになることに注意しておこう。

図７：関手\(h^A\)の性質

それでは証明に移る。図８において、真ん中の図が可換図式になればよいので、\(F(f)(φ_{F,A})=φ_{F,X}(N(f))\)が成り立つことを示せばよい。従って、この図の左右にある二つのストリング・ダイアグラムが同値であることを示せばよい。

図８：\(A\)に対して自然であるときは上の図式は可換図式となる。

ストリング・ダイアグラムを用いての変形を図９に示す。

図９：\(A\)に対して自然であることをストリング・ダイアグラムを用いて証明する。

それでは、細部を見ていこう。(1)から(2)は\(F(f)\)と\(φ_{F,A} \partial\)を切り離し、その間で、\(FA\)が受け渡しされるので、それを明示。(2)から(3)は\(φ_{F,A} \partial =\partial_A I_A\)を利用。(3)から(4)は\(f \in h^A (X) \)を利用。(4)から(5)は\(h^f = h^X \rightarrow h^A\)と\(I_X=h^X(X)\)を利用。 (5)から(6)は\(N(f) \partial = \partial h^f\)(図１０参考) *1を利用。(6)から(7)は\( φ_{F,X} \partial^{\prime} = \partial_X^{\prime} I_X, \partial_X^{\prime} =N(f) \partial \)より導かれる。

図１０：\(N(f) \partial_Y= \partial_Y^{\prime}\)を証明するための参考図

それでは、最後に\(F\)に対して自然であるについて考える。

先ほどと同様に、図１１において、真ん中の図が可換図式になればよいので、\(μ_A (φ_{F,A} ) = φ_{G,A} (M(μ))\)が成り立つことを示せばよい。従って、この図の左右にある二つのストリング・ダイアグラムが同値であることを示せばよい。

図１１：\(F\)に対して自然であるときは上の図式は可換図式となる。

ストリング・ダイアグラムを用いての変形を図１２に示す。

図１２：\(F\)に対して自然であることをストリング・ダイアグラムを用いて証明する。

それでは、細部を見ていこう。(1)から(2)は\(μ_A\)と\(φ_{F,A} \partial\)を切り離し、その間で、\(FA\)が受け渡しされるので、それを明示。(2)から(3)は\(φ_{F,A} \partial =\partial_A I_A\)を利用。(3)から(4)は\(M(μ) \partial_Y =μ_Y\partial_Y\)(図１３参考) を利用。(4)から(5)は\( φ_{G,A} M(μ) \partial = M(μ) \partial_A I_A \)を利用。

図１３：\(M(μ) \partial_Y =μ_Y\partial_Y\)を証明するための参考図

これで、米田の補題を証明することができた。式を展開しての証明よりは、ストリング・ダイアグラムを用いてのビジュアルな証明の方が理解しやすかったのではと期待しているのだが、読者の方はどうでしたか。

機会があれば、ストリング・ダイアグラムについて再度触れてみたいと思っている。

*1:\(\partial_Y \in Nat(h^A(Y),F(Y) ) \),\(\partial_Y^{\prime} \in Nat(h^X(Y),F(Y) ) \)としたとき、\(N(f) \partial_Y= \partial_Y^{\prime}\)である。図１０に示すように、\(h^f(Y) :h^X(Y) \rightarrow h^A(Y), \partial_Y: h^A(Y) \rightarrow F(Y) \)より、\( \partial_Y^{\prime} : h^X (Y) \rightarrow F(Y) = \partial_Y h^f(Y) \)である。従って、\(N(f) \partial = \partial h^f\)となる。

圏論：ストリング・ダイアグラム ー 表現可能関手

３．表現可能関手

世の中のものにはそれぞれ名前がついているのが普通で、いちいちその由来を考えることはないが、時々なぜと頭を悩ませるものがある。表現可能関手(representable functor)もその一つだ。この関手が、何を表現可能にしてくれるのだろうと考えこんでしまう。その都度適当な解釈を見出してその場をしのいでいたのだが、どうも的確であったようには思えない。

Ulrich Goertz, Torsten Wedhornが著わした”Algebraic Geometry I”の8章では、表現可能関手を取り上げている。その冒頭で表現可能を言い換えて、幾何学的な対象(geometric object)と言っている。この本は代数幾何学について説明しているので、幾何学的な対象は、(多変数)多項式の解の集合を表した空間図形(楕円、放物線、双曲線など)だろうと推測できる。

ところで、代数幾何学の基本的な考え方はイデアル(ideal)にあると考えてよい(イデアルは環論(ring theory)とも呼ばれる)。イデアルは整数の性質を調べるために考え出された概念で、倍数や素数などのそれが明らかにされ、その考え方は、多項式の解の集合(空間図形)へと拡張された。とても大雑把に言ってしまうと、空間図形を数の集合として、逆に数の集合を空間図形として扱ってしまおうとするのが代数幾何学である。そして空間図形と数の集合を結びつける概念を表す一つの方法として、表現可能関手が導き出された。

表現可能関手の素性が分かったところで、これをストリング・ダイアグラムで表すという本題に戻ることにしよう。なお代数幾何学は統計学、学習理論、深層学習などに応用され、情報科学・工学の分野ではとても役に立つ基礎理論の一つになっている。

３．１　表現可能関手の定義

それでは定義から始めよう。\(\mathcal{C}\)を局所的に小さい圏とし、\(\mathbf{Set}\)を集合の圏とする。\(\mathcal{C}\)の対象\(A \)に対して関手\({\rm Hom} (A,-) \)は、\(\mathcal{C}\)の対象\(X\)を集合\({\rm Hom} (A,X) \)に写像するものとする。

「定義」：　関手\(F:\mathcal{C} \rightarrow \mathbf{Set}\) が、\(\mathcal{C}\)のある対象\(A \)において\({\rm Hom} (A,-) \)への自然同型であるとき、\(F\)を表現可能という。また\(F\)の表現とは、\( φ:{\rm Hom}(A,-) \cong F \) を満たす対\( (A, φ) \)のことである。

「定理」：　この定義から次の定理が導かれる。関手\(F\)が表現可能であるとき、ある\(a \in F(A)\)において、全ての\( x \in F(X) \)に対して、\( (Ff) a = x\)とするような射\(f\)が一意的に存在する。また、その逆も言える。

それではこの定理を、ストリング・ダイアグラムを用いて証明することを考えよう。

３．２　証明の準備

証明に入る前に少し準備をしておこう。表現可能関手に関連する圏と関手は図１のように表すことができる。

図１：表現可能関手\(F\)とそれに関連する圏、関手、自然変換

図で、関手\(h^A={\rm Hom}_\mathcal{C}(A,-) \)から関手\(F\)への自然変換は\(α\)とした。\(F\)が表現可能であることから、各成分での自然変換に対して逆の自然変換が存在する。すなわち\(A\)と任意の\(X\)に対して、
\begin{eqnarray}
β_A \circ α_A &=& I_{h^A(A)} \\
α_A \circ β_A &=& I_{F(A)} \\
β_X \circ α_X &=& I_{h^A(X)} \\
α_X \circ β_X &=& I_{F(X)}
\end{eqnarray}
となるような\(β\)が存在する。

関手\(h^A\)の役割についても説明しておこう。

図２左に示すように、関手\(h^A={\rm Hom}_\mathcal{C}(A,-)\)は、\(\mathcal{C}\)の対象\(X\)を\(\mathbf{Set}\)の集合\({\rm Hom}_\mathcal{C}(A,X)\)に写像する。また\(\mathcal{C}\)の射\(f:X \rightarrow Y\)を\(h^A(f)\)に写像する。このとき、図２右に示すように
\begin{eqnarray}
h^A(f)= f \circ h^A: {\rm Hom}_\mathcal{C}(A,X) \rightarrow {\rm Hom}_\mathcal{C}(A,Y)
\end{eqnarray}
である。

図２：共変関手\(h^A\)の役割

共変関手\(h^A\)を用いて表現可能関手を定義したが、反変関手\(h_A={\rm Hom}_\mathcal{C}(-,A)\)を用いても同様に表現可能関手を定義できる。このときは、関手\(F:\mathcal{C} \rightarrow \mathbf{Set}\) が\(\mathcal{C}\)のある対象\(A \)において\(h_A (={\rm Hom} (-,A) ) \)への自然同型であるとき\(F\)を表現可能という、となる。関手\(h_A\)の役割は次のようになる。

図３左に示すように、関手\(h_A={\rm Hom}_{\mathcal{C}^{op}}(-,A)\)は、\(\mathcal{C}^{op}\)の対象\(X\)を\(\mathbf{Set}\)の集合\({\rm Hom}_{\mathcal{C}^{op}}(X,A)\)に写像する。また\(\mathcal{C}^{op}\)の射\(f:Y \rightarrow X\)を\(h_A(f)\)に写像する。このとき、図３右に示すように
\begin{eqnarray}
h_A(f)= h_A \circ f : {\rm Hom}_{\mathcal{C}^{op}}(X,A) \rightarrow {\rm Hom}_{\mathcal{C}^{op}}(Y,A)
\end{eqnarray}
である。

図３：反変関手\(h_A\)の役割

３．３　定理の証明

それでは、関手\(F\)が表現可能であるとき、ある\(a \in F(A)\)において、全ての\( x \in F(X) \)に対して、\( (Ff) a = x\)とするような射\(f\)が一意的に存在することを証明しよう。図４に示すように、例によって圏\(1\)を設け、圏\(\mathcal{C}\)の対象\(A,X\)を、圏\(1\)から\(\mathcal{C}\)への関手として表すことにする。なお図４下はpasting diagramである。

図４：表現可能関手をストリング・ダイアグラムに表すために圏\(1\)を設け、圏\(\mathcal{C}\)の対象\(A,X\)を圏\(1\)からの関手とする

\(\mathcal{C}\)の対象\(A,X\)を関手\(F,H^A\)によって圏\( \mathbf{Set} \)に写像したとき、図５中に示す可換図が得られる。ここで\(α\)は\(h^A\)から\(F\)への、\(β\)は\(F\)から\(h^A\)への自然変換である。可換図であることから、\(F(A)\)から\(F(X)\)への変換は経路に寄らない。このため図５左の\(h^A(A),h^A(X)\)を経由するストリング・ダイアグラムと、図５右の直接たどり着くストリング・ダイアグラムとは、同値となる。

図５：同値なストリング・ダイアグラム

図５左のストリング・ダイアグラムを変形すると図６となる。

図６：左側のストリング・ダイアグラムを変形する。

これにより\(x = (Ff) a \)であることが示された。

そこで次に\(f\)が一意に決まることを示そう。\(f\)のほかに\(g\)があったとしよう。図５右のストリングダイアグラムの\(f\)を\(g\)に置き換えて変形すると、図７右に示すような変形が得られる。右からの変形と先に示した左からの変形は同値であることから、\(f=g\)となる。これで証明は終了である。

図７：\(f\)が一意であることの証明

さて次はいよいよ米田の補題を示そう。

圏論：ストリング・ダイアグラム ー 異なる随伴の定義が同値であることの証明

２．２　余単位-単位随伴による定義

随伴の定義には先に説明したもののほかに、いくつかの同値な言い換えがある。その中で、よく知られているものに、余単位(counit)-単位(unit)随伴がある。これは次のように定義される。

圏\(\mathcal{C}\)と\(\mathcal{D}\)の余単位-単位随伴とは、二つの関手\(L: \mathcal{D} \rightarrow \mathcal{C}\)と\(R: \mathcal{C} \rightarrow \mathcal{D}\)、および二つの自然変換
\begin{eqnarray}
ε: LR \rightarrow I_\mathcal{C} \\
η: I_\mathcal{D} \rightarrow RL
\end{eqnarray}
があり、図１２に示すような可換図式となるときである(これを三角可換図式と呼ぶ)。そして\(ε\)と\(η\)はそれぞれ余単位と単位、\(L\)は\(R\)の左随伴、\(R\)は\(L\)の右随伴と呼ばれる。

図１２：余単位-単位随伴を成り立たせる可換図式

上記の可換図式を等式で表すと、
\begin{eqnarray}
I_L=εL \circ Lη \\
I_R=Rε \circ ηR
\end{eqnarray}
となる。

２．３　証明をストリング・ダイアグラムで行う

それでは、先に説明した随伴の定義から、今回の余単位-単位を用いての定義が導き出されることを、ストリング・ダイアグラムを用いて証明しよう。

\begin{eqnarray}
Φ_{A,B}:{\rm Hom}_\mathcal{C} (LB,A) \cong {\rm Hom}_\mathcal{D} (B,RA)
\end{eqnarray}
より、\(Φ_{A,B}Φ^{-1}_{A,B}g = g\)となるので、\(g \in h^BRA\)を関手\(L\)で圏\(\mathcal{C}\)に移すと、これに対応した射\(f \in h^{LB}A\)となる。さらに関手\(R\)で圏\(\mathcal{D}\)に移すと、\(g\)に戻る。これはストリング・ダイアグラムで表すと、図１３となる。

図１３：\(g \in h^BRA\)を一回りさせたものと、元のものとが同じであることを表したストリング・ダイアグラム

右側を変形すると、図１４となる。

図14：一回りした\(g\)のストリング・ダイアグラムを変形する。

これを見やすくすると、図１５の中央の図となる。そして、これと左側の図とは等しい。

図１５：一回りした\(g\)と、もとの\(g\)とがストリングダイアグラムで表す。

三角可換図式に対応する部分を抜き出すと図１６となる(\(g\)より左側の部分)。この左図で下の方から上の方に移動していくと、\(R\)から、\(Rη\)に達し、そこを越えたところから\(RLR\)となり、さらに上に行くと\(εR\)となり、ついに\(R\)に至ることが分かる。そして右図は左図と同値であるので、図１２の三角可換図式(右側)と同じであることが分かる。

図１６：三角可換図式の一つを導き出した。

同じように、\(f \in h^{LB}A\)についても考えることができ、一回りしてきたものと、そのままとが等しいというストリング・ダイアグラムは図１７となる。

図１７：\(f \in h^{LB}A\)を一回りさせたものと、元のものとが同じであることを表したストリング・ダイアグラム

これの右側を変形すると、図１８の中央の図となる。これとその右側の図とは等しい。

図１８：一回りした\(f\)のストリング・ダイアグラムを変形する。

三角可換図式に対応する部分を抜き出すと、図１９を得る。これからこの図は図１２の三角可換図式(左側)と同値であることが分かる。

図１９：三角可換図式の残りの一つを導き出した。

これによって、随伴の二つの定義が同値であることが証明できたが、ストリング・ダイアグラムを用いての証明は、このようにビジュアルで分かりやすい。

圏論：ストリング・ダイアグラム ー 随伴

２．　随伴

ストリング・ダイアグラムでの表現にも慣れてきたので、いきなりジャンプして、圏論の真髄ともいえる随伴について考えることにしよう。

２．１　随伴の定義

ウィキペディアでは、随伴を次のように定義している(但しここでは記号は変えてある)。

圏\(\mathcal{C}\)と圏\(\mathcal{D}\)との間の随伴とは、二つの関手
\begin{eqnarray}
L: \mathcal{D} \rightarrow \mathcal{C} \\
R: \mathcal{C} \rightarrow \mathcal{D}
\end{eqnarray}
の対であって、全単射の族(集合)
\begin{eqnarray}
Φ_{A,B}:{\rm Hom}_\mathcal{C} (LB,A) \cong {\rm Hom}_\mathcal{D} (B,RA)
\end{eqnarray}
が変数\(A\),\(B\)に関して自然となるものをいう。なお\(L\)は\(R\)の左随伴、\(R\)は\(L\)の右随伴という。これは図１のように表すことができる。

別の言い方をすると、任意の射\(f \in {\rm Hom}_\mathcal{C} (LB,A) \)を取りだしたとき、これに対して\(Φ_{A,B}f=g\)となるような\(g \in {\rm Hom}_\mathcal{D} (B,RA)\)が唯一つ存在し、逆もまた真であるといえる。

図１：随伴の定義

これからは\(f\)や\(g\)のように、射の集合の１要素を扱うことになるので、これをストリング・ダイアグラムでどのように表現できるかあらかじめ議論しておこう。

\(h^A B = {\rm Hom}(A,B) \)が集合(族)であるとする。集合が便利な点は、それが要素を有するということである。そこで射の集合\(h^A B\)からの任意の一つの射を\(fA\)と表すことにしよう。\(f^A\)と表してもよいのだが、ここでは\(fA\)とし、これは\(A\)をドメインとした射\(f\)ということにする。\(f\)のコドメインを\(B\)とすると、\(f \in h^A B\)は図２のストリング・ダイアグラメで表すことができる。丁度、集合の要素を表現したものと同じような感じである。

図２：\(\rm Hom\)集合の１要素をストリング・ダイアグラムで表す。

感覚的にあっているというだけでは、数学としての扱いができないので、この表現に矛盾がないかを調べよう。図３に示すように、一つの対象だけを有する圏\(1\)から、圏\(\mathcal{C}\)の対象\(A\)に対して関手を張る。このとき一つではなく、2つの関手\(*,A\)を張ったとし、この関手間の自然変換を\(A\)としよう。

図３：\(\rm Hom\)集合の１要素を表すために圏\(1\)を利用する。

これをストリング・ダイアグラムで表すと図４となり、図２の表現には問題がないことが分かる。これで集合の要素としての射を表すことができるようになったので、随伴に関わる性質を考えていこう。

図４：圏\(1\)を利用して\(\rm Hom\)集合の１要素をストリング・ダイアグラムで表す。

随伴に関しても、図５に示すように、圏\(1\)から、圏\(\mathcal{C}\)の対象\(A\)への関手\(A\)と、圏\(\mathcal{D}\)の対象\(B\)への関手\(B\)を設けて議論を進めることができる。

図５：随伴の定義に対しても圏\(1\)を利用する。

任意の射\(f \in h^{LB} A \)を取りだすと、これに対して\(Φ_{A,B}f=g\)となるような\(g \in h^B RA \)が唯一つ存在するという随伴の定義は、図６に示すように、\(B\)から出発して\(A\)に到達する経路は二つあるが、これらは可換であると言い換えることができる。

図６：随伴の定義のうち、任意の射\(f \in h^{LB} A \)に対して、唯一つの\(g \in h^B RA \)が存在することに対応した可換図式

このため、任意の\(f \)に対して、唯一つの\(g \)が存在するということは、(1) \(LB\)をドメインとして\(f\)を施して得たコドメイン\(A\)と、(2) \(B\)をドメインとして\(g\)を施して得たコドメインを関手\(L\)によって\(\mathcal{C}\)の側に移した\(A\)とには、(1)と(2)とも\(B\)からスタートして同じところに至ると言い換えることができるので、ストリング・ダイアグラムで表すと図７のようになる。

図７：可換図式をストリング・ダイアグラムで表す。

それでは図７の右側を変形すると図8になる。ここで(1)はスタート。(2)は\(LgB\)を詳細にしたもの。(3)は\(ε: LR \rightarrow I_\mathcal{C}\)で置き換えたもの。(4)は(3)を見やすくしたものである。

図８：ストリング・ダイアグラムを変形して、\(ε: LR \rightarrow I_\mathcal{C}\)を得る。

逆の場合についても考えてみよう。今度は任意の射\(g \in h^B RA \)を取りだすと、これに対して\(Φ^{-1}_{A,B}g=f\)となるような\(f \in h^{LB} A \)が唯一つ存在するという場合である。図９に示すように、\(B\)から出発して\(RA\)に到達する経路は二つあるが、これらは可換である。

図9：随伴の定義のうち、任意の射\(g \in h^B RA \)に対して、唯一つの\(f \in h^{LB} A \)が存在することに対応した可換図式

前と同じようにこの関係をストリング・ダイアグラムで示すと図１０となる。

図１０：可換図式をストリング・ダイアグラムで表す。

前と同じように右側を変形すると、図１１を得る。ここでは(2)から(3)に移行するときに、\(η: I_\mathcal{D} \rightarrow RL \)を用いた。

図１１：ストリング・ダイアグラムを変形して、\(η: I_\mathcal{D} \rightarrow RL \)を得る。

ここで得られた\(ε,η\)を用いても随伴を同じように定義することができる。これについては次の記事にしよう。