1.8 錐の例
今年のブログの締めは、少しでも圏論が身近に感じられるようにするために、錐の例を取り上げよう。
前回のブログで、抽象度の高い、下図のような極限の可換図式を示した。

この可換図式は、錐を作成すると、それがどのような極限なのかを、示してくれる。
上図で、圏\(C\)は、対象となっているのは錐だけで、射となっているのは錐の頂点間の写像という極めて簡素な圏である。
圏\([\mathcal{I,C}]\)はインデックス圏\(I\)から圏\(C\)への関手によって、錐がどのような構造を持っているかを示した圏である。
それでは、いくつかの例を示そう。
1)終対象
最初は、底面のない錐である。圏\(\mathcal{C}\)があった時、その対象は底面のない錐であったとしよう。その中には、極限と呼ばれる錐\(C’\)が存在する。これを\(LimD\)と記述しよう。これを下図の左側に示す。
そして、圏\(\mathcal{C}\)から任意の対象\(C\)を取り出そう。\(C\)も\(C’(=LimD)\)も錐であり、そして、\(C’\)は極限の錐であることから、\(m:C \rightarrow C’\)となる一意に定まる関数が存在する。そして、\(f:C’ \rightarrow C\)とした時、\(m= contramap \ f\)となる。これらの関係を下図の真ん中に示す。
これらの関係については、下図を参照のこと。錐の頂点は正確に記述すると\(\mathcal{C}(C',LimD)\),\(\mathcal{C}(C,LimD)\)だが、ここでは、簡略して\(C',C\)と記述している。
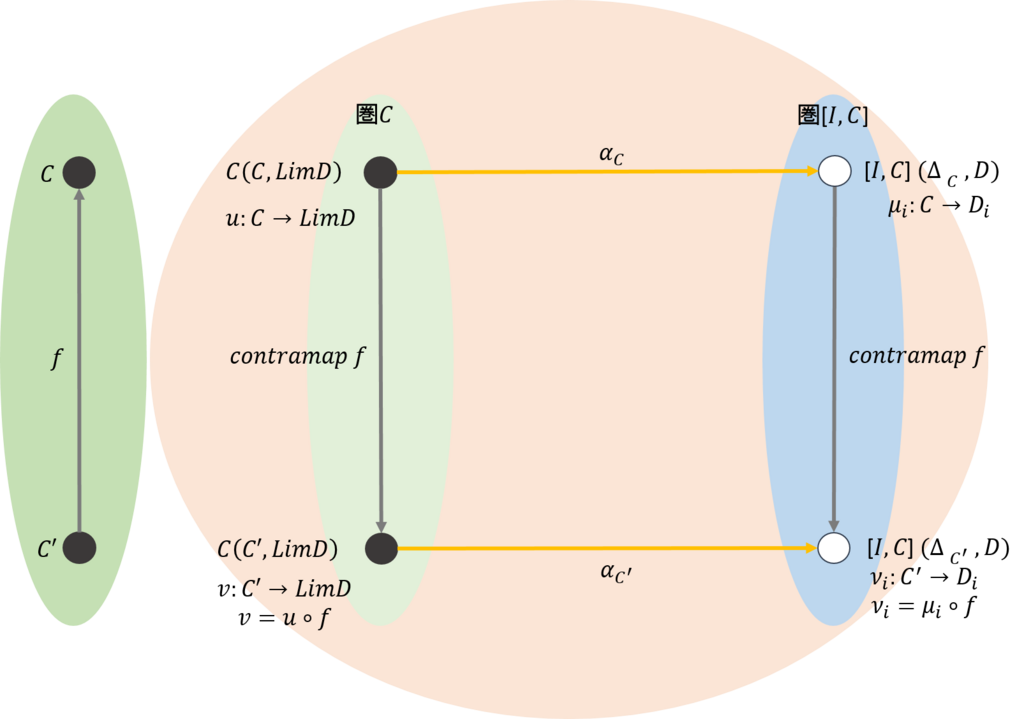
これを圏\([\mathcal{I,C}]\)に移すと、下図の右側の図となる。これは、任意の対象について成り立っていることから、任意の対象\(\Delta_C\)から\(\Delta_{LimD}\)への射\(contramap \ f\)が存在することとなり、\(\Delta_{LimD}\)は終対象となる(なお、\(contramap \ f \)は圏\(\mathcal{C}\)と圏\([\mathcal{I,C}]\)で同一に記述しているが、構造は似ているものの異なる関数であることに注意しておこう)。
従って、頂点だけの錐は、極限が終対象となることが分かる。

2)積、デカルト積、冪
次の例を示そう。次の圏\(C\)は、底面は有するが、2頂点だけで、辺を持たない錐を対象にしているものとする。それを、下図の右側に示す。
前回の例と同じように、錐\(C,C’\)を定めることにしよう。\(C’=limD\)は極限の錐である。これを示したのが、下図の左側と真ん中である。
そして、これを圏\([\mathcal{I,C}]\)に移してみよう。これは、圏\(\mathcal{C}\)の積であることが分かる。

もう少し、分かりやすく示したのが下図である。

底辺の頂点をさらに具体的にすると下図のようになる。底辺の頂点\(A,B\)が集合である時は、下図の右側に示すように、錐の頂点\(A \times B\)はデカルト積\((A,B)\)となる。
また、底辺の頂点\(X,Y\)を写像のドメインとコドメインと考えると、\(X \times Y\)は定数関数となり、冪\(Y^X\)で表される。(なお、\(X\)から\(Y\)への写像は、\(X\)の集合の要素の数を\(X\)とし、\(Y\)の集合の要素の数を\(Y\)とすると、定数関数の数は、\(Y^X\)となる。これを利用して、関数をこのように冪を用いて表現している)。

3)イコライザ
さらに、例を示そう。次の圏\(C\)は底面に2頂点を有し、一方の頂点から他方の頂点へ二つの射\(f,g\)があるものとする。これを、下図の右側に示す。
前回の例と同じように、錐\(C,C’\)を定めることにしよう。\(C’=limD\)は極限の錐である。これを示したのが、下図の左側と真ん中である。

これを、圏\([\mathcal{I,C}]\)に移すと上図の左側の図になる。
かつて、イコライザの説明をした時に、これを次のように定義した。
「イコライザの定義」適当な対象\(E\)と射\(eq:E \rightarrow X\)で\(f \circ eq = g \circ eq\)を満たすものの組\((E,eq)\)が存在し、任意の対象\(O\)と射\(m:O \rightarrow X\)の組\((O,m)\)で、\(f \circ m = g \circ m\)が与えられた時、射\(u:O \rightarrow E\)が\(eq \circ u = m\)を満たすものが一意的に存在するとき、\((E,eq)\)をイコライザという。
下図に示すように、圏\([\mathcal{I,C}]\)はイコライザの定義そのものである。従って、底辺の2頂点間で同一方向に二つの射が存在するとき、極限はイコライザとなる。

4)引き戻し
さらに、例を示そう。次の圏\(C\)は底面に3頂点を有し、二つの頂点から残りの一つの頂点への写像が存在するものである。それを下図の右側に示す。

この例はデータベースである。具体的に示そう。ある学年の名簿を作成したと仮定しよう。そして、上の図に示すように、錐の頂点はデータベースという対象である。ここには、男子学生、女子学生、組のテーブルがある。男子学生のテーブルには、名前を記載するフィールドと所属する組を示すフィールドがある。女子学生のテーブルも同じである。また、組のテーブルは、クラスの名前を記入する。
データベースからの射が、男子学生、女子学生、クラスと呼ばれる集合で、これらは錐の底辺での頂点となる。そして、頂点間では、男子学生と女子学生からクラスへの射が設けられている。
ここで、射の方向を変えて、クラスの側から男子学生あるいは女子学生を観察したらどのようになるであろうか。例えば、A組に属している男子学生を求めたとしたら、それは、{太郎、次郎、…}というように構成員の集まりとなる。通常、写像はコドメインとなっている集合の要素を与えてくれるが、この場合は、集合を与えてくれる。
このような場合、上図に示すように、男子学生からクラスへの写像の値が一致する男子学生の集合を表すために一本の線を引き、その線上に構成要素を記述する。これは、数学の用語では、ファイバーと呼んでいる。ホモトピーなどを学ぶときなどに、必要とされる概念である。
また、この錐の極限を、引き戻し、あるいはファイバー積という。
宿題:上記のデータベースを極限を用いてHaskellで実現しなさい。
年が明けたら、極限と双対関係にある、余極限について説明する。それでは、良いお年をお迎えください。