Netwireでゲームを作成する（５）

８．各圏へのインスタンス化

前回の記事で、振舞いを次のように定義した。

newtype Behavior t a b = Behavior { stepBehavior :: t -> a -> (b,Behavior t a b) }

この段階では、型として定義しただけなので、いろいろな性質を持たせるために、必要な型クラスのインスタンスにする。以下で、インスタンス化を行うが、そこでは、いくつかのモジュールを必要とする。それを示したのが下記である。

{-# LANGUAGE TemplateHaskell #-}

import Control.Lens
import Control.Arrow
import Control.Category
import Prelude hiding ( (.), id )
import Control.Applicative
import Data.Semigroup

８．１　Arrowのインスタンスに

Arrowはスイッチを表現するために、なくてはならない型クラスである。過去の記事で、Yampaの信号関数を説明するときにArrow記法に触れた。Arrow記法を用いることで、逐次処理、分岐(スイッチ)、繰り返しが可能になる。

型クラスArrowは次のようにCategoryのサブクラスとして定義されている。Arrowはメソッドとしてarrとfirstを有する。

class Category a => Arrow a wherewhere
  arr :: (b -> c) -> a b c
  first :: a b c -> a (b,d) (c,d)

Haskellのよいところは、あるいは、圏論のよいところは、抽象度の高い定義に対して多様な解釈を許すことである。型クラスArrowもとても抽象度が高いので様々な見方から説明できる。例えば、Yampaでの信号関数のように、あるいは、Haskell/Understanding arrowsの記事にみられるように、Arrowを工場に見立て、写像を機械とみなし、機械をコンベアの上に載せることで実現できる逐次処理、並行処理、並列処理などを例示して説明できる。このように、顧客にあわせて説明できるので、抽象度の高い定義はとても便利である。このことが、ドメイン固有言語を容易に作成できる能力をHaskellに与えている。

arrの定義は、カリー化したときの可換図式を思い出してほしい。

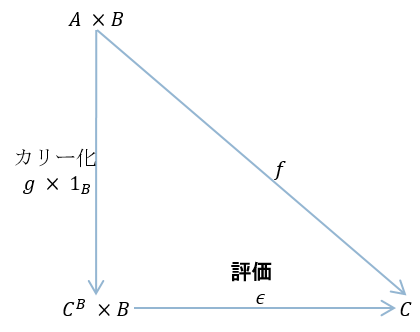
上記の図で、\(f: A \times B \rightarrow C\)をカリー化すると\(g: A \rightarrow C^B\)となる。arrの定義は、指数対象\(C^B\)が与えられた時、カリー化関数で対象Aから\(C^B\)への写像を与えていると考えればよい。

firstの定義は次のように説明できる。まず、上記の可換図式から次の可換図式を得る。

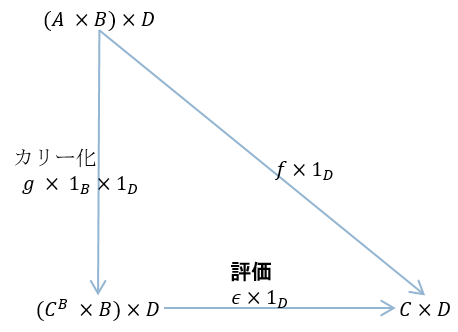
firstは上記の可換図式のカッコの部分、すなわち左側(first)の部分を表したものである。右側の\( \times D \)はごみのようなものだ。

しかし、この可換図式を下記のように書き換えることが可能である。

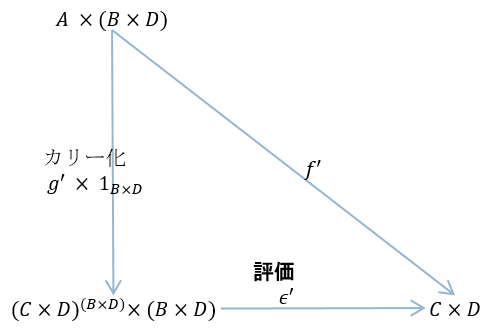
型シグネチャでの右側の項はこれを表したものである。

この型クラスには次の制約がある。なお、下記で(>>>)は関数合成である。通常は、(.)を用いるが、ここではArrowの通例に従った。

arr id = id
arr (f >>> g) = arr f >>> arr g
first (arr f) = arr (first f)
first (f >>> g) = first f >>> first g
first f >>> arr fst = arr fst >>> f                     -- fstは対のペアの最初の要素
first f >>> arr (id *** g) = arr (id *** g) >>> first f -- ***は後で説明
first (first f) >>> arr assoc = arr assoc >>> first f where assoc ((a,b),c) = (a,(b,c))

上記で、arr f >>> arr gの部分で用いられている(>>>)の型シグネチャは、

(>>>) :: a b c -> a c d -> a b d

である。
arr,first,(>>>)を図で表すと以下のようになる。

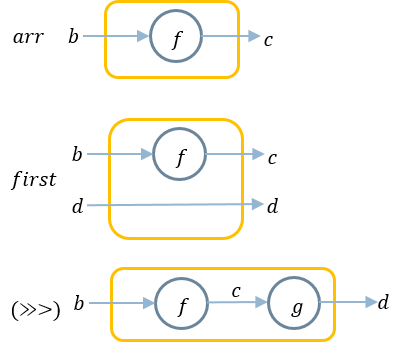
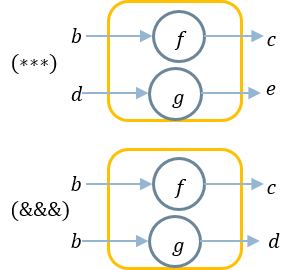
arrowで用意した関数arr, firstを利用して次の有用な関数を作成できる。

(***) :: a b c -> a d e -> a (b, d) (c, e)
(&&&) :: a b c -> a b d -> a b (c, e)

そこで、型Behaviorを以下のようにして型クラスArrowのインスタンスにする。

fix f = f (fix f)

instance Arrow (Behavior t) where
  arr f = fix $ \r -> Behavior $ \t a -> (f a,r)
  first f = Behavior $ \t (b,d) ->
    let (c,fn) = stepBehavior f t b
    in ((c,d),first fn)

８．２　Categoryのインスタンスに

BehaviorをArrowのインスタンスにしたので、そのスーパークラスであるCategoryのインスタンスにもしておく必要がある。

Categoryは、圏論での圏である。圏は、①対象の集まりを有する②射の集まりを有する③射はドメインからコドメインへと写像する④恒等射が存在する⑤関数の合成が存在するであった。また、満たさなければならない条件は、①恒等射に対しては単位律が成り立つ。即ち、いかなる射に恒等射を(右からでも左からでも)施しても、元の射になる。②関数を合成したとき、結合律が成り立つ。即ち、どの部分から関数の合成を計算しても変わらないである。

Categoryの定義は次のようになっていて、メソッドとして恒等射idと合成(.)を有する。

class Category cat where
  id :: cat a a 
  (.) :: cat b c -> cat a b -> cat a c

そこで、Behaviorを次のようにして、Categoryのインスタンスとする。

instance Category (Behavior t) where
  id = arr id
  x . y = Behavior $ \t a ->
    let (yr, yn) = stepBehavior y t a
        (xr, xn) = stepBehavior x t yr
    in (xr, xn . yn)

上記で、x.yは、aという入力を受けて、yがyrという出力を出し、xはyrという入力を受けて、xrという出力を出す。また、この時、yの新しい振舞いはynになり、xの新しい振舞いはxnになる。

８．３　Semigroupのインスタンスに

集合\(S\)と二項演算が与えられ、そこで、結合律が成り立つとき半群という。1以上での自然数での加算は半群の例である。自然数の加算では0が恒等射であるが、半群は恒等射があることを要求していない。

Categoryの定義は次のようになっていて、メソッドとして二項演算子<>を有する。

class Semigroup a where
  (<>) :: a -> a -> a

振舞いについても、出力と振舞いの型が同じである時、二つの振舞いを一つの振舞いにまとめられるように、次のようにインスタンス化する。

instance (Semigroup b) => Semigroup (Behavior t a b) where
  x <> y = Behavior $ \t a ->
    let (xr,xn) = stepBehavior x t a
        (yr,yn) = stepBehavior y t a
    in (xr <> yr,xn <> yn)

８．４　Functorのインスタンスに

キーボードからのイベントを処理するときに、Functorを用いた。そこで、Behaviorをこのインスタンスとする。Functorについては馴染んでいる人も多いと思うが、その定義は次のようになっている。また、メソッドとしてfmapを有する。

class Functor f where
  fmap :: (a -> b) -> f a -> f b

なお、次の規則を満たさなけらばならない。

  fmap id == id
  fmap (f . g) == fmap f . fmap g

Behaviorは、次によりFunctorのインスタンスにする。

instance Functor (Behavior t a) where
  fmap f b = Behavior $ \t a ->
    let (br,bn) = stepBehavior b t a
    in (f br,fmap f bn)

８．５　ApplicativeとProfunctorのインスタンスに

使い勝手を良くするために、ApplicativeとProfunctorのインスタンスにもする。これは次のように行う。
なお、ApplicativeとProfunctorについては、別の記事で説明する予定である。

Applicativeの定義は次のようになっている。pureという関数は後続の記事でキーボードの入力を速度に変換するときに使用する。

class Functor f => Applicative f where
  pure :: a -> f a 
  (<*>) :: f (a -> b) -> f a -> f b

インスタンス化は次のように行う。

instance Applicative (Behavior t a) where
  pure = arr . const
  f <*> x = Behavior $ \t a ->
    let (fr,fn) = stepBehavior f t a
        (xr,xn) = stepBehavior x t a
    in (fr xr,fn <*> xn)

Profunctorの定義は次のようになっている。

class Profunctor h where
  dimap :: (c -> a) -> (b -> d) -> f a b -> f c d

インスタンス化は次のように行う。

instance Profunctor (Behavior t) where
  dimap l r x = Behavior $ \t a ->
    let (xr,xn) = stepBehavior x t (l a)
    in (r xr,dimap l r xn)