2.2 射
圏論の中で一番重要な役割を担うのは射(arrowあるいはmorphism)である。射は対象を対象へと移す(写像という用語を使ったときは「写す」といったほうがよさそうだが、射は矢を射るという意味で用いているので「移す」という漢字を使う)。射は、他の分野では写像と呼ばれたり、関数と呼ばれたりする。しかし、圏論では、写像や関数の概念を抽象化して用いるので、射という特別な用語を用いる。
1)射とは
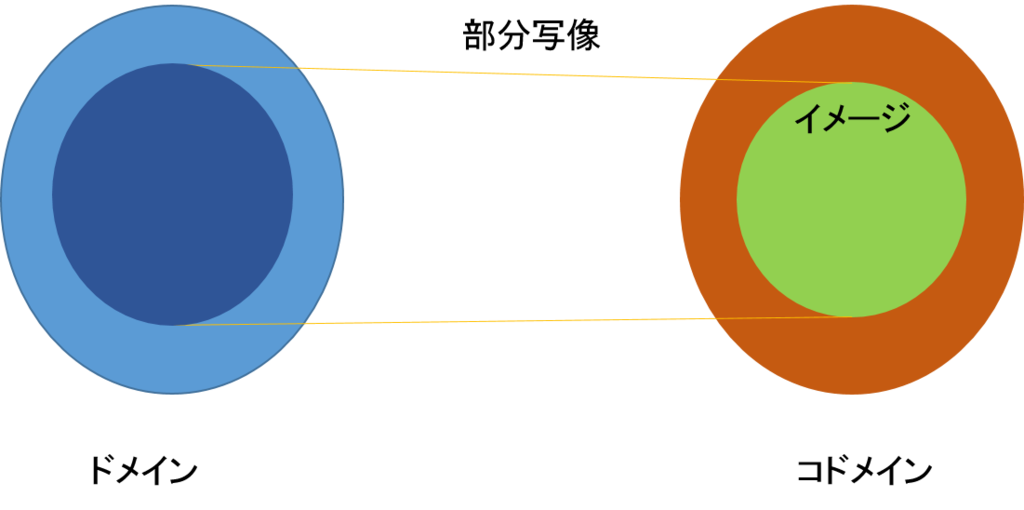
射\(f\)は、\(f:A \rightarrow B\)と記述される。\(A,B\)は対象で、\(A\)をドメイン(domain)、\(B\)はコドメイン(codomain)と呼ばれる。また、\(f(A)\)、即ち、ドメイン\(A\)が射\(f\)によって移される先をイメージ(Image)と呼ぶ。

2)部分写像は射ではない
射の定義はかなり自由だが、それでもいくつか制限がある。その一つは、ドメインのいずれの要素も射によってコドメインのある要素に移されなければならない。しかし、反対に、コドメインの全ての要素が射のイメージになっている必要はない。射によって、全部であったり一部であったりしてよい。
関数では、このような関数を全関数(total function)と呼んでいる。しかし、我々が使っている写像の中には、全写像とはならないものがあることに注意しておく必要がある。例えば、お見合いパーティーをしたとしよう。パーティーに参加する人の情報をあらかじめ与えておいて、一番気に入っている人を当日会場の入り口で提出することにしよう。そして、相互に名前が一致した人達だけが、最初にお見合いをすることとする。この時、男性をドメインに、女性をコドメインにして、お見合いの相手を男性の方から女性の方に写像したとする。しかし、残念なことに、お見合いの相手がいない男性もいるであろう。このような場合には、ドメインのある要素に関数が定義されない。このようなものは部分写像(partial mapping)あるいは部分関数(partial function)と呼ばれるが、これは、集合と(全域)写像の圏の射ではない。
部分関数は、あるもの同士の関係を表す時によく現れる。例えば、データベースではこのようになっている場合が多い。
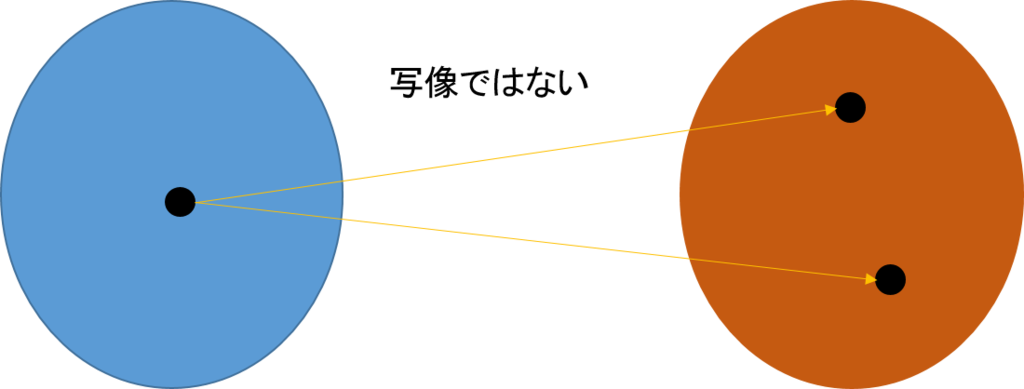
また、関数は、一つの要素に複数の要素が対応することを許してはいないので、このようなものも圏論での射とはならない(ただし、関数の逆関数はこのようになることがある)。
3)倍数を求める射
それでは、射の例をいくつか挙げてみよう。ドメインもコドメインも1で始まる自然数とする。射は2倍にする関数*2とする。この時の射は次のようになる。イメージは偶数となり、コドメインより小さい領域となる。

それでは、上の射をHaskellで実現してみよう。Haskellでは射は関数という用語を使っているので、慣習に従って、Haskellのプログラムを説明しているときは、関数という用語を用いる。また、対象もデータ型という用語を用いる。
Haskellは自然数のデータ型を用意していないので、自分で用意する必要がある。そこで、次のように定めよう。
data Nat1 = One | Succ Nat1 deriving (Read, Eq, Ord, Show)
とても短い定義だ。\(One\)は自然数1に対応する。\(Succ \ Nat1\) は自然数\(Nat1\)に続く自然数を表す。従って、\(Succ \ One\)は自然数1に続く自然数ということで2を表す。以下同様に、\(Succ \ (Succ \ One)\)は3である。
ところで、これではわかりにくいので、正の整数から対応する自然数を作り出す関数\(toNat1\)を用意しよう。これは以下のようにする。なお、記述\(toNat1 :: Int \rightarrow Nat1\)は次のことを意味する。関数\(toNat1\)はデータ型Intをデータ型\(Nat1\)へ移す。
toNat1 :: Int -> Nat1 toNat1 m | m == 1 = One | m > 0 = Succ $ toNat1 (m - 1) | otherwise = error "Not Natural Number"
また、逆に自然数から対応する整数を作り出す関数\(fromNat1\)も次のように用意しよう。
fromNat1 :: Nat1 -> Int fromNat1 One = 1 fromNat1 (Succ n) = 1 + fromNat1 n
それでは少し使ってみよう。自然数1から順番に求めてみよう。また、逆への変換も行ってみる。
Prelude> :load "Nat1.hs" [1 of 1] Compiling Main ( Nat1.hs, interpreted ) Ok, modules loaded: Main. *Main> let v1 = toNat1 1 *Main> v1 One *Main> let v2 = toNat1 2 *Main> v2 Succ One *Main> let v3 = toNat1 3 *Main> v3 Succ (Succ One) *Main> let v4 = toNat1 4 *Main> v4 Succ (Succ (Succ One)) *Main> let v8 = toNat1 8 *Main> v8 Succ (Succ (Succ (Succ (Succ (Succ (Succ One)))))) *Main> fromNat1 v1 1 *Main> fromNat1 v2 2 *Main> fromNat1 v8 8
それでは与えられた自然数の2倍を求める関数を求めてみよう。名前は、*2ではなく\(times2\)とする(*2はHaskellで既に使われているので、これとの混用を避ける)。2倍を求めるためには、与えられた数同士を加えればよい。そのためには、自然数を足し合わせる関数plusが必要になるので、これも一緒に定義することにしよう。次のようになる。
plus :: Nat1 -> Nat1 -> Nat1 m `plus` One = Succ m m `plus` Succ n = Succ (m `plus` n) times2 :: Nat1 -> Nat1 times2 m = m `plus` m
関数\(plus\)は少し説明が必要である。自然数\(m\)と\(One\)を加えると、\(m\)に続く自然数\(Succ \ m\)となる。また、自然数\(m\)と\(Succ \ n\) (\(n\)に続く自然数)を加算すると、自然数\(m\)と\(n\)を加算して得られた自然数に続く自然数となる。これらを表したのが、上の定義である。なお、\(plus\)を中置関数として利用するときは、関数の前後に\(`\)をつけて、\(`plus`\)とする。さて、完成したので、実験してみよう。同じように自然数1から始めて、だんだんに数を大きくしてみる。
Prelude> :load "Nat1.hs" [1 of 1] Compiling Main ( Nat1.hs, interpreted ) Ok, modules loaded: Main. *Main> let v1 = toNat1 1 *Main> let v1_2 = times2 v1 *Main> v1 One *Main> v1_2 Succ One *Main> let v2 = toNat1 2 *Main> let v2_2 = times2 v2 *Main> v2 Succ One *Main> v2_2 Succ (Succ (Succ One)) *Main> let v3 = toNat1 3 *Main> let v3_2 = times2 v3 *Main> v3 Succ (Succ One) *Main> v3_2 Succ (Succ (Succ (Succ (Succ One)))) *Main> let v7 = toNat1 7 *Main> let v7_2 = times2 v7 *Main> fromNat1 v7 7 *Main> fromNat1 v7_2 14
なお、上の定義で、関数\(times2\)は、\(times2 :: Nat1 \rightarrow Nat1\)という記述があったが、ここれは次のことを意味する。写像\(times2\)がデータ型\(Nat1\)をデータ型\(Nat1\)へ移す。これは圏論の用語を用いて説明すれば、射\(times2\)が対象\(Nat1\)を対象\(Nat1\)へ移すということになる。
4)剰余を求める射
それでは、ドメイン、コドメインは自然数だが、0始まりとする。そして、3で割った時の余りを求める関数を\(mod3\)とした時の射を求めてみよう。イメージは0,1,2となり、コドメインよりもずっと小さい領域である。

それではHaskellで実現してみよう。0から始まる自然数\(Nat0\)を、先ほどの1から始まる自然数と同様に、定義してみよう。その時、一緒に、自然数と整数の間で変換する関数\(toNat0,fromNat0\)も定義しよう。以下のようになる。
data Nat0 = Zero | Succ Nat0 deriving (Read, Eq, Ord, Show) toNat0 :: Int -> Nat0 toNat0 m | m == 0 = Zero | m > 0 = Succ $ toNat0 (m - 1) | otherwise = error "Not Natural Number" fromNat0 :: Nat0 -> Int fromNat0 Zero = 0 fromNat0 (Succ n) = 1 + fromNat0 n
それでは、関数\(mod3\)を実現してみよう。次のようになる。
mod3 :: Nat0 -> Nat0 mod3 Zero = Zero mod3 (Succ Zero) = Succ Zero mod3 (Succ (Succ Zero)) = Succ (Succ Zero) mod3 (Succ (Succ (Succ m))) = mod3 m
使ってみよう。自然数0から始めて少しずつ数を大きくして調べてみる。
Prelude> :load "Nat0.hs" [1 of 1] Compiling Main ( Nat0.hs, interpreted ) Ok, modules loaded: Main. *Main> let v0 = toNat0 0 *Main> v0 Zero *Main> mod3 v0 Zero *Main> let v1 = toNat0 1 *Main> v1 Succ Zero *Main> mod3 v1 Succ Zero *Main> let v2 = toNat0 2 *Main> v2 Succ (Succ Zero) *Main> mod3 v2 Succ (Succ Zero) *Main> let v3 = toNat0 3 *Main> v3 Succ (Succ (Succ Zero)) *Main> mod3 v3 Zero *Main> let v4 = toNat0 4 *Main> v4 Succ (Succ (Succ (Succ Zero))) *Main> mod3 v4 Succ Zero *Main> let v15 = toNat0 15 *Main> v15 Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ Zero)))))))))))))) *Main> mod3 v15 Zero
5)複数の射
今度は、射が二つある場合を考えてみよう。対象を\(A={f,g,h},V={a,b,c,d}\)とする。また、射\(arc,trg\)はドメインを\(A\)とし、コドメインを\(V\)とし、下図のように移すとする。

圏は抽象化されたものなので、それに対応させて様々な具体例を作ることができるが、上の射を実現したような実例を挙げることができるであろうか。下図はどうであろうか。

上の図からわかるように、グラフは矢印をドメインとし、接続点をコドメインとし、矢印の元の方を接続点に移す射\(src\)と、矢印の先の方を接続点に移す射\(trg\)を用意することで圏となる。
5)可能な射をすべて求める
それでは、\(A={1,2,3}\)と\(B={a,b}\)の二つの対象があり、\(A\)をドメイン、\(B\)をコドメインとする射はいくつあるだろうか。ただし、同じ射は含めないとする。正解は下図のように\(2^3=8\)である。

上の結果をHaskellで確かめてみよう。
ドメインとコドメインを次のデータ型\(Domain,Codomain\)で定義しよう。
data Domain = D1 | D2 | D3 deriving (Read, Show) data Codomain = CA | CB deriving (Read, Show)
可能な射をリストとして出力されるようにしよう。即ち、リストの要素は一つの射に対応するものとする。また、それぞれの射は、ドメインの要素とコドメインの要素の対とする。それぞれの対では、ドメインの要素はその射によって移されるコドメインの要素に移されるものとする(リストが入れ子になっていることに注意)。これを実現したのが、下記のプログラムである。
morphism :: [((Domain, Codomain), (Domain, Codomain), (Domain, Codomain))] morphism = [((D1,d1), (D2,d2), (D3,d3)) | d1 <- [CA, CB], d2 <- [CA, CB], d3 <- [CA, CB]]
この関数を実行してみよう。
Prelude> :load "Morphism.hs" [1 of 1] Compiling Main ( Morphism.hs, interpreted ) Ok, modules loaded: Main. *Main> morphism [((D1,CA),(D2,CA),(D3,CA)),((D1,CA),(D2,CA),(D3,CB)),((D1,CA),(D2,CB),(D3,CA)),((D1,CA),(D2,CB),(D3,CB)),((D1,CB),(D2,CA),(D3,CA)),((D1,CB),(D2,CA),(D3,CB)),((D1,CB),(D2,CB),(D3,CA)),((D1,CB),(D2,CB),(D3,CB))]
上記の結果で、リストの要素が一つの射を表しているので、可能な射は、
\(( (D1,CA),(D2,CA),(D3,CA) )\)
\(( (D1,CA),(D2,CA),(D3,CB) )\)
\(( (D1,CA),(D2,CB),(D3,CA) )\)
・・・
の8個である。これは、先ほど示したものと一致する。
また、上記の射は、ドメインの要素とそれによって移されるコドメインの要素を示している。最初の射では、\(D1\)を\(CA\)に、\(D2\)を\(CA\)に、\(D3\)を\(CA\)に移す。
6)個数\(m\)のドメインから個数\(n\)のコドメインへの射
一般にドメインの要素数が\(m\)でコドメインの要素数が\(n\)のとき、異なる射の数は\(n^m\)となる。
いくつか確認してみよう。コドメインの要素数が1の時は、異なる射の数は1個である。例えば、ドメインを自然数とすると、射は次のようになる。

それでは、ドメインの要素数を1としよう。この時は異なる射の数はコドメインの要素の数となる。例えば、コドメインが自然数であったとすると次のようになる(図では\(one,two,three\)まで書いたが、そのあと無限に続く)。

それでは、ドメインの要素数が0の時は、どうであろうか。式からは1となる。そこで、ドメインが空集合の時は、コドメイン全体に移す射が一つあることにする。

それでは、Haskellでドメインの要素数が\(m\)でコドメインのそれが\(n\)の時の関数をすべて求めてみよう。
このプログラムは相当に手ごわいので、少しずつ部品を用意しながら、完成に導こう。今、ドメインの要素数が3であり、要素は順番に\(a1,a2,a3\)となっていったとしよう。これをリストで表すと\([a1,a2,a3]\)となる。一方、コドメインの要素数は2であり、順番に\(b1,b2\)であったとする。ドメインの要素に対してコドメインの要素を対応させることになるが、ドメインの右の方から処理していくことにする。
最初に、行うのは、\(a3\)となる。そこで、\(a3\)を\(b1,b2\)で置き換えたリストを\([[b1],[b2]]\)とする。次に\(a2\)を置き換えて、それを先ほど得たリストの頭にくっつけることにしよう。そうすると、\([[b1,b1],[b1,b1],[b2,b1],[b2,b2]]\)をえる。さらに、\(a1\)についても同じことを行えば、ドメインからコドメインに移す異なる射をすべて得ることができる。
そこで、置き換えられたリストから次の要素も置き換えたリストを作る関数\(addRep\_\)を定義しよう。
addRep_ :: [b] -> [[b]] -> [[b]] addRep_ [] _ = [] addRep_ _ [] = [] addRep_ (y:ys) (l:ls) = (y:l) : addRep_ [y] ls ++ addRep_ ys (l:ls)
確認してみよう。
*MorphismA> addRep_ [1,2] [[1],[2]] [[1,1],[1,2],[2,1],[2,2]]
うまく動いているようである。それでは、この操作を左端から右端まで再帰的に順番に行う関数\(morphism\_\)を定義しよう。
morphism_ :: [a] -> [b] -> [[b]] morphism_ _ [] = [] morphism_ [] ys = [ys] morphism_ (x:[]) (y:ys) = [y] : morphism_ (x:[]) ys morphism_ (x:xs) ys = addRep_ ys $ morphism_ xs ys
上の関数で、左端についての処理を行うのが、以下の部分である。
morphism_ (x:[]) (y:ys) = [y] : morphism_ (x:[]) ys
途中の処理は次の部分である。
morphism_ (x:xs) ys = addRep_ ys $ morphism_ xs ys
すでに置き換えの済んでいるリスト\(morphism\_ \ xs \ ys\)に新しい置き換え\(addRep\_ \ ys\)を付け加えている。
正しく動いているかどうか確認してみよう。
*MorphismA> morphism_ [1,2,3] [1,2] [[1,1,1],[1,1,2],[1,2,1],[1,2,2],[2,1,1],[2,1,2],[2,2,1],[2,2,2]] *MorphismA> morphism_ ['a', 'b', 'c'] [1,2] [[1,1,1],[1,1,2],[1,2,1],[1,2,2],[2,1,1],[2,1,2],[2,2,1],[2,2,2]]
うまく動いているようだ。
また、プログラムで
morphism_ [] ys = [ys]
は、空集合に対する射である。次のようになる。
*MorphismA> morphism_ [] [1,2] [[1,2]]
全体への射となる。
さて、部品が完成したので、これはモジュール\(MorphingA\)としておこう。
module MorphismA (morphism_) where morphism_ :: [a] -> [b] -> [[b]] morphism_ _ [] = [] morphism_ [] ys = [ys] morphism_ (x:[]) (y:ys) = [y] : morphism_ (x:[]) ys morphism_ (x:xs) ys = addRep_ ys $ morphism_ xs ys addRep_ :: [b] -> [[b]] -> [[b]] addRep_ [] _ = [] addRep_ _ [] = [] addRep_ (y:ys) (l:ls) = (y:l) : addRep_ [y] ls ++ addRep_ ys (l:ls)
要素の数が与えられた時は、配列を自動的に作り出して、\(morphism\_\)を呼び出して、可能な関数をリストの列で与える関数\(morphism\)を次のように定義する。
morphism :: (Num b, Num a, Enum b, Enum a) => a -> b -> [[b]] morphism m n = morphism_ [1..m] [1..n]
これの動作を確認しよう。
*Main> morphism 3 2 [[1,1,1],[1,1,2],[1,2,1],[1,2,2],[2,1,1],[2,1,2],[2,2,1],[2,2,2]]
うまく動いているようである。
上記では、ドメインからコドメインへの射は配列、例えば[1,1,1]、で与えられているが、これをタプル、即ち(1,1,1)、で表すことにしよう。
これは、コドメインの要素数ごとに関数を用意する。要素数が0に対しては\(morphism0、1\)に対しては\(morphism1、2\)に対しては\(morphism2\)のように定義しよう。次のようになる。
morphism0 :: (Num a, Enum a) => a -> [[a]] morphism0 n = morphism 0 n morphism1 :: (Num a, Enum a) => a -> [a] morphism1 n = toPair1 $ morphism_ [1..1] [1..n] where toPair1 [] = [] toPair1 (f:fs) = (f !! 0) : toPair1 fs morphism2 :: (Num a, Enum a) => a -> [(a, a)] morphism2 n = toPair2 $ morphism_ [1..2] [1..n] where toPair2 [] = [] toPair2 (f:fs) = (f !! 0, f !! 1) : toPair2 fs morphism3 :: (Num a, Enum a) => a -> [(a, a, a)] morphism3 n = toPair3 $ morphism_ [1..3] [1..n] where toPair3 [] = [] toPair3 (f:fs) = (f !! 0, f !! 1, f !! 2) : toPair3 fs morphism4 :: (Num a, Enum a) => a -> [(a, a, a, a)] morphism4 n = toPair4 $ morphism_ [1..4] [1..n] where toPair4 [] = [] toPair4 (f:fs) = (f !! 0, f !! 1, f !! 2, f !! 3) : toPair4 fs morphism5 :: (Num a, Enum a) => a -> [(a, a, a, a, a)] morphism5 n = toPair5 $ morphism_ [1..5] [1..n] where toPair5 [] = [] toPair5 (f:fs) = (f !! 0, f !! 1, f !! 2, f !! 3, f !! 4) : toPair5 fs morphism6 :: (Num a, Enum a) => a -> [(a, a, a, a, a, a)] morphism6 n = toPair6 $ morphism_ [1..6] [1..n] where toPair6 [] = [] toPair6 (f:fs) = (f !! 0, f !! 1, f !! 2, f !! 3, f !! 4, f !! 5) : toPair6 fs
分かりやすいところから、実行してみよう。ドメインとコドメインとも要素数が2の場合は次のようになる。
*Main> morphism2 2 [(1,1),(1,2),(2,1),(2,2)]
これは次のように解釈される。射は4個ある。それらは、(1,1),(1,2),(2,1),(2,2)である。最初の射(1,1)は、ドメインの最初の要素をコドメインの最初の要素に、そして、ドメインの最後の要素をコドメインの最初の要素に移す。ここで、ドメインの要素の順番は適当でよい。コドメインについても同じである。
*Main> morphism3 2 [(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2)]
4では、
*Main> morphism4 2 [(1,1,1,1),(1,1,1,2),(1,1,2,1),(1,1,2,2),(1,2,1,1),(1,2,1,2),(1,2,2,1),(1,2,2,2),(2,1,1,1),(2,1,1,2),(2,1,2,1),(2,1,2,2),(2,2,1,1),(2,2,1,2),(2,2,2,1),(2,2,2,2)]
だいぶ関数が多くなってきた。関数の数を数えてみよう。今得た結果に\(length\)を施すと求めることができる。
*Main> length $ morphism4 2 16
要素数が5と6の時についても求めてみよう。
*Main> length $ morphism4 2 16 *Main> length $ morphism5 2 32 *Main> length $ morphism6 2 64
*Main> morphism1 2 [1,2]
本当は、[(1),(2)]と表示されることを望んだのだが、()がなくても同じということで、省かれている。
ドメインの要素数が1の時の射を求めてみよう。
*Main> morphism0 2 [[1,2]] *Main> length $ morphism0 2 1
全体に移され、射の総数は1である。
それでは、コドメインの要素数を変えてみよう。1個の場合はどうであろうか。
*Main> morphism0 2 *Main> morphism6 1 [(1,1,1,1,1,1)] *Main> morphism5 1 [(1,1,1,1,1)] *Main> morphism4 1 [(1,1,1,1)] *Main> morphism2 1 [(1,1)] *Main> morphism1 1 [1] *Main> morphism0 1 [[1]]
射の数はどれも1であることが確認できる。
それでは0の場合はどうであろうか。
*Main> morphism6 0 [] *Main> morphism5 0 [] *Main> morphism4 0 [] *Main> morphism3 0 [] *Main> morphism2 0 [] *Main> morphism1 0 [] *Main> morphism0 0 []
個数は0だ。
Haskellでは空集合をデータ型Data.Voidで定義している。その中に、\(absurd\)という関数があって、\(Void\)を任意の型に移している。
Prelude> import Data.Void Prelude Data.Void> :i Void data Void -- Defined in ‘Data.Void’ instance [safe] Eq Void -- Defined in ‘Data.Void’ instance [safe] Ord Void -- Defined in ・eData.Void’ instance [safe] Read Void -- Defined in ‘Data.Void’ instance [safe] Show Void -- Defined in ‘Data.Void’ Prelude Data.Void> :t absurd absurd :: Void -> a
論理学では\(Void\)は偽の値を持つ。\(Absurd\)の関数を\(if \ Void \ then \ a\)とみなすならば、\(Void\)が偽であることから、\(a\)は何であったもよいことになる。即ち、任意の型でよいことになる。このことを表しているのが、\(absurd\)だが、使う機会はなさそうである。
7)星の上の対象
圏論を勉強しているときに、下記の図を見てびっくりした。驚愕したという方が適切かもしれない。

この図を見るまでは自然数は対象にしかならないと思い込んでいたが、なんとここでは射になっている。全く異質な世界を見せられた。射であるからには、自然数はあるものをあるものに移さなければならない。図では星を星に移していた。明らかに対象なのだが、なぜ、星で表しているのであろうか。
圏論の入門書を読むと、最初の方に対象の詳細を知ることなしに、論じることができる数学の体系を考えようという趣旨のことが書かれている。対象は集合やグラフなど様々な構造を持っている。その構造に重点を置いて論じると、集合論やグラフ理論や位相空間論などの様々な数学の分野に落ち込んでしまう。そこで、構造を気にしないで論じてみようというのが圏論だ。
しかし、圏論の入門書を読んでいると、集合から初めてグラフへと説明が移行していくので、圏論の本来の趣旨をすっかり忘れて、対象の構造にどっぷりしたって考える癖がついてしまう。そのような時に出会ったのが、上の図である。
星が対象の本体の趣旨を思い出させてくれた。星が表しているのは対象なのでその中身は気にしないでねというメッセージを送ってくれている。とても高尚な表現である。
この図が持つ正確な意味は、射と射の合成を論じてからでないと、説明できない。従って、ここでは問題の提起だけにして、楽しい話はしばらく後にしよう。