6.1 関手の定義
圏論は数学的な構造を対象としての点と対象を結ぶ射としての矢印で表している。二つの圏があった時に、片方の構造を他方のそれに写像するのが関手である(注意:集合はいわゆる写像を有しないので、恒等射のみを有する圏である。このような圏は離散圏(discrete category)と呼ばれる)。
例を挙げて説明しよう。今、二つの圏\(\mathcal{C}\)と\(\mathcal{D}\)があり、前者は対象\(A,B\)と射\(f:A \rightarrow B\)と恒等射\(id_A,id_B\)で構成されているとする。関手\(F\)は前者の構造を後者に写像する。すなわち、図に示すように \(\\\)
\(A,B\)を\(F (A),F (B)\)に、\(\\\)
\(f:A \rightarrow B\)を\(F (f): F (A) \rightarrow F (B)\)に、\(\\\)
\(id_A,id_B\)を\(F (id_A),F (id_B)\)に写像する。

この時、\(\mathcal{D}\)での対象\(F (A)\)と\(F (B)\)に対する恒等射\(id_{F(A)}\)と\(id_{F(B)}\)はそれぞれ\(F (id_A)\)と\(F (id_B)\)であることに注意して欲しい。
射\(f\)を関手\(F\)で写像するということが理解しにくいかと思う。\(A\)から\(B\)への射は一つとは限らない。複数あっても構わない。そこで、これらを集合と見なすことができる。そこで、\(A\)から\(B\)への射の集合を\({\rm HOM}(A,B)\)と記述する。もし、圏を明記する必要があるときは、\({\rm HOM}\)に添え字で圏の名前を付す。例えば、\({\rm HOM}_\mathcal{C} (A,B)\)とする。このようにすると\(F (f): {\rm HOM}_\mathcal{C} (A,B) \rightarrow {\rm HOM}_\mathcal{D} (F (A),F (B))\)となる。これは集合から集合への写像なので、通常の関数の概念と同じになるので、理解しやすいと思う。
集合から集合への写像なので、単射(injective)であるのか全射(surjective)であるのかが気になるが、関手はこれらの性質を問わない。単射であってもそうでなくても構わない。即ち1対1対応である必要はない。また、全射であってもそうでなくても構わない。即ち、写像される側のすべての要素に写像される必要はない。但し、関手が単射であるとき忠実(faithful)関手といい、全射であるとき充満(full)関手という。
圏の構造の一つの特徴は、射の合成である。そこで合成を伴う圏の関手を考えることにしよう。圏\(\mathcal{C}\)は対象\(A,B,C\)と射\(f:A \rightarrow B, g:B \rightarrow C \)と恒等射\(id_A,id_B,id_C \)で構成されているとする。射は合成できるので、\(g \circ f:A \rightarrow C \)が存在する。この構造を、図に示すように、関手\(F\)で圏\(\mathcal{D}\)に写像することを考えよう。

\(A,B,C\)は\(F (A),F (B),F (C)\)に、 \(\\\)
\(f:A \rightarrow B\)と\(g:B \rightarrow C \)は\(F (f): F (A) \rightarrow F (B)\)と\( F (g): F (B) \rightarrow F (C) \)に、 \(\\\)
\(id_A\)と\(id_B\)と\(id_C\)は\(F (id_A)\)と\(F (id_B)\)と\(F (id_C) \)にそれぞれ写像される。
また、\(g \circ f:A \rightarrow C \)は\(F ( (g \circ f) ): F (A) \rightarrow F (C) \)に写像される。一方、\(F (f)\)と\(F (g)\)は合成できるので、これは\(F (g) \circ F (f): F (A) \rightarrow F (C) \)となる。圏論では、構造を保持する必要があるので、\(F (g \circ f)= F (g) \circ F (f)\)となる。
関手のいくつかの例を挙げてみよう。
最初の例はシングルトンだけから成り立つ圏からの関手である。これは相手側の対象を一つ選択する件である。

次の例は、定関手(constant functor)と呼ばれるものである。すべての対象が一つの対象に写像される。また、すべての対象が恒等射に写像される。
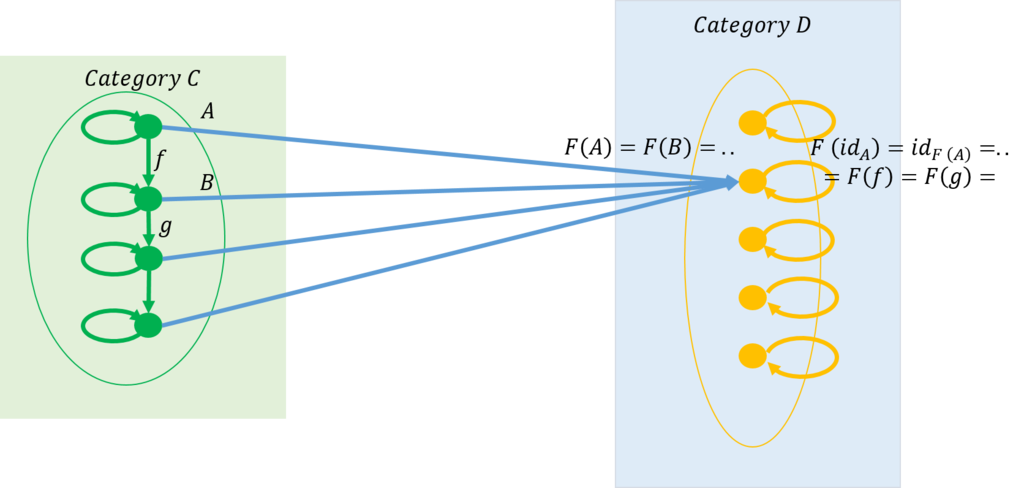
最後の例は自己関手(endofunctor)と呼ばれる。プログラミング言語もこの例の一つである。
それではHaskellのプログラムで関手を使ってみよう。Haskellでは対象は型としてあらわされる。また、型シグネチャを用いて、入力されるデータの型や出力されるデータの型を示す。この時、型はその時の状況によって決まることが多いので、通常は、型そのもので表さず、型変数というものを用いる。実際に関数を利用するときに、型変数が型にバインディングされる。
\(Maybe\)という型を考えることにする。これは次のように定義する。
data Maybe a = Nothing | Just a
最初の図をHaskellの流儀で表したものが次の図である。

この図では、\(F\)は対象に対しては\(Maybe\)を、射に対しては\(fmap\)を用いている。また、対象は型変数となるので小文字で書いてある。それでは、関手を定義してみよう。
fmap :: (a -> b) -> (Maybe a -> Maybe b) fmap f Nothing = Nothing fmap f (Just x) = Just (f x)
プログラムを作って実行してみよう。Maybeは用意されているので、これとの混同を避けるために、新しく定義するMaybeには句読点をつけて定義しよう。即ち次のようにする。
data Maybe' a = Nothing' | Just' a deriving (Eq, Show, Read) fmap' :: (a -> b) -> (Maybe' a -> Maybe' b) fmap' f Nothing' = Nothing' fmap' f (Just' x) = Just' (f x)
実行してみよう。
Prelude> :load "maybe.hs" [1 of 1] Compiling Main ( maybe.hs, interpreted ) Ok, modules loaded: Main. *Main> fmap' (+3) (Just' 4) Just' 7 *Main> fmap' (++ "!!") (Just' "Happy") Just' "Happy!!"
\(Maybe\)という関手を定義したが、これが関手であるためには、構造を保持していなければならない。次の記事では構造が保たれていることを示すことにしよう。