5.6 代数的データ型
引き続き、Bartosz Milewskiの動画を元に、話を進める。
1) 乗算(Multiply)
デカルト積の圏について、前々回の記事で説明したが、積と名前がついているので、四則演算での乗算とかかわりがありそうである。
乗算\(\times\)は、交換律(commutative property)、結合律(associative property)、単位元(identity element)の存在、ゼロの存在(property of zero)という性質を持つ。
デカルト積の圏にもこれらの性質を持たすことができれば、このような性質を持った圏と乗算の圏は同じ構造の圏になりそうだ。そこで、これらの性質を持たせるように工夫してみよう。
デカルト積の圏で\((a,b)\)と表されるものは、乗算では\(a \times b \)と表されるものとする。
次は交換律である。値の順序を入れ替えても結果は同じという性質なので、デカルト積の圏の方には、\(mswap\)という射を用意する。即ち、
\begin{eqnarray}
mswap \ p = (snd \ p, fst \ p)
\end{eqnarray}
次は結合律である。計算の順番によらないという性質なので、デカルト積の圏の方には、\(massoc,massoc\_inv\)という射を用意する。即ち、
\begin{eqnarray}
massoc \ ( (x,y),z) = (x, (y,z) ) \\
massoc\_inv \ ( x,(y,z) ) = ( (x, y ),z )
\end{eqnarray}
また、デカルト積の圏では1は()に対応させることとする。従って、単位元に対する演算\(a \times 1 = a\)と\(a =a \times 1\)は、\(munit, munit\_inv\)で表すと次のようになる。
\begin{eqnarray}
munit \ (x,() )= x \\
munit\_inv \ x = (x,( ) )
\end{eqnarray}
さらに、0は\(Void\)に対応させることとする。演算\(a \times 0 = 0\)は、\(mzero\)で表すと次のようになる。
\begin{eqnarray}
mzero :: (a,Void ) \rightarrow Void
\end{eqnarray}
ただし、型コンストラクタ\(Void\)は次に示すように値コンストラクタを有しない。このため、関数は値コンストラクタを用いて定義されるので、シグネチャは定義できるが、その関数は定義できない(前後が逆になるが、型コンストラクタ、値コンストラクタについてはすぐ後で説明する)。
Prelude> import Data.Void Prelude Data.Void> :i Void data Void -- Defined in ‘Data.Void’
これまでの説明をまとめたのが、以下の表である。
| 規則 | 積の圏(Haskell) | 乗算 |
|---|---|---|
| 解釈 | \((a,b)\) | \(a \times b \) |
| 交換律 | \(mswap :: (a, b) \rightarrow (b, a) \\ mswap \ p = (snd \ p, fst \ p)\) | \(a \times b = b \times a \) |
| 結合律 | \(massoc :: ( (a,b),c) \rightarrow (a, (b,c) ) \\ massoc \ ( (x,y),z) = (x, (y,z) ) \) | \((a \times b) \times c = a \times (b \times c) \) |
| \(massoc\_inv :: ( a,(b,c) ) \rightarrow ( (a, b),c ) \\ massoc\_inv \ ( x,(y,z) ) = ( (x, y ),z ) \) | \(a \times (b \times c) = (a \times b) \times c \) | |
| 単位元 | \(munit :: (a,() ) \rightarrow a \\ munit \ (x,() )= x\) | \(a \times 1 = a \) |
| \(munit\_inv :: a \rightarrow (a,() ) \\ munit\_inv \ x = (x,( ) )\) | \(a = a \times 1 \) | |
| ゼロ | \(mzero :: (a,Void ) \rightarrow Void \) | \(a \times 0 = 0 \) |
これをHaskellのプログラムとして実装してみよう。
import Data.Void mswap :: (a,b) -> (b,a) mswap p = (snd p, fst p) massoc :: ((a,b),c) -> (a,(b,c)) massoc ((x,y),z) = (x,(y,z)) munit :: (a,()) -> a munit (x,()) = x munit_inv :: a -> (a,()) munit_inv x = (x,()) --mzero :: (a, Void) -> Void
少し、利用してみよう。
Prelude> :load "product.hs" [1 of 1] Compiling Main ( product.hs, interpreted ) Ok, modules loaded: Main. *Main> mswap (3,4) (4,3) *Main> massoc ((3,4),5) (3,(4,5)) *Main> massoc_inv (6,(7,8)) ((6,7),8) *Main> munit (4,()) 4 *Main> munit_inv 5 (5,())
2) 加算(Sum)
次は余積の圏だ。余積は和と書かれることもあるので、加算と関係があるはずだ。
余積の圏は\(Either \ a \ b \)と記述していたが、これを\(a+b\)と思うことにしよう。\(+\)の左側には\(a\)があって、右側には\(b\)があると思うことにする。このようにすると、
加算が有する、交換律、結合律、単位元の存在などの性質は乗算の時と同じように、余積の圏に持たせることができる。
交換律は射\(sswap\)で表すことにすると次のようになる。\(mswap\)とは異なり単純な関数では済まない。左側\(Left\)の値が来た場合と右側\(Right\)の値が来た場合に応じて、計算の仕方を変える必要がある。
\begin{eqnarray}
sswap \ (Left \ x) = Right \ x \\
sswap \ (Right \ x) = left \ x
\end{eqnarray}
次は交換律である。交換律では3個の値を使うことになるので、対(ペア)のデータ型だけでは結果を表すことができない。そこで、新しいデータ型を用意する。
data Tripple a c b= Left' a | Middle' c | Right' b deriving (Eq, Show, Read)
これを用いると結合律の射\(asspc, assoc\_inv \)は次のように定義できる。
\begin{eqnarray}
sassoc (Left \ x) = Left' \ x \\
sassoc (Right \ (Left \ x) ) = Middle' \ x \\
sassoc (Right \ (Right \ x) ) = Right' \ x \\
sassoc\_inv (Left \ (Left \ x) ) = Left' \ x \\
sassoc\_inv (Left \ (Right \ x) ) = Middle' \ x \\
sassoc\_inv (Right \ x) = Right' \ x
\end{eqnarray}
加算の時の単位元は0である。余積の圏でも0を\(Void\)で表すことにする。単位元に関連する演算\(sunit,sunit\_inv\)は、シグネチャだけになり、次のようになる。
\begin{eqnarray}
sunit :: Either \ a \ Void \rightarrow a \\
sunit\_inv :: a \rightarrow Either \ a \ Void
\end{eqnarray}
\(Either \ a \ Void\)の解釈だが、左側からは\(a\)という値が取り出せる。しかし、右側からは何も出てこない。従って、二つを足し合わせると、\(a\)になるというものだ。
これらを表にまとめると次のようになる。
| 規則 | 余積の圏(Haskell) | 乗算 |
|---|---|---|
| 解釈 | \(Either \ a \ b\) | \(a + b \) |
| 交換律 | \(sswap :: Either \ a \ b \rightarrow Either \ b \ a \\ sswap \ (Left \ x) = Right \ x \\ sswap \ (Right \ x) = left \ x \) | \(a + b = b + a \) |
| 結合律 | \(sassoc :: Either \ a \ (Either \ c \ b) \rightarrow Tripple \ a \ c \ b \\ sassoc (Left \ x) = Left' \ x \\ sassoc (Right \ (Left \ x) ) = Middle' \ x \\ sassoc (Right \ (Right \ x) ) = Right' \ x\) | \((a + c) + b = a + (c + b) \) |
| \(sassoc\_inv :: Either \ (Either \ a \ c) \ b \rightarrow Tripple \ a \ c \ b \\ sassoc\_inv (Left \ (Left \ x) ) = Left' \ x \\ sassoc\_inv (Left \ (Right \ x) ) = Middle' \ x \\ sassoc\_inv (Right \ x) = Right' \ x \) | \(a + (c + b) = (a + c) + b \) | |
| 単位元 | \(sunit :: Either \ a \ Void \rightarrow a\) | \(a + 0 = a \) |
| \(sunit\_inv :: a \rightarrow Either \ a \ Void \) | \(a = a + 0 \) |
Haskellのプログラムで記述してみよう。次のようになる。
import Data.Void data Tripple a c b= Left' a | Middle' c | Right' b deriving (Eq, Show, Read) sswap :: Either a b -> Either b a sswap (Left x) = Right x sswap (Right x) = Left x sassoc :: Either a (Either c b) -> Tripple a c b sassoc (Left x) = Left' x sassoc (Right (Left x)) = Middle' x sassoc (Right (Right x)) = Right' x sassoc_inv :: Either (Either a c) b -> Tripple a c b sassoc_inv (Left (Left x)) = Left' x sassoc_inv (Left (Right x)) = Middle' x sassoc_inv (Right x) = Right' x --sunit :: Either a Void -> a --sunit_inv :: a -> Either a Void
実行してみよう。
Prelude> :load "coproduct.hs" [1 of 1] Compiling Main ( coproduct.hs, interpreted ) Ok, modules loaded: Main. *Main> let a = Left 3 *Main> let b = Right 4 *Main> sswap a Right 3 *Main> sswap b Left 4 *Main> let c = Right (Left 5) *Main> let d = Right (Right 6) *Main> sassoc a Left' 3 *Main> sassoc c Middle' 5 *Main> sassoc d Right' 6 *Main> let e = Left (Left 7) *Main> let f = Left (Right 8) *Main> sassoc_inv e Left' 7 *Main> sassoc_inv f Middle' 8 *Main> sassoc_inv b Right' 4
3) 分配律(Distributive Property)
加算と乗算が出てきたので、分配律についても確認しよう。これは\(a \times ( b + c) = a \times b + a \times c \)である。従って、()と\(Either\)を用いて次のように表すことができる。
| 規則 | 積・余積の圏(Haskell) | 乗算と加算 |
|---|---|---|
| 分配律 | \(distr :: (a, Either \ b \ c) \rightarrow Either \ (a, b) \ (a, c) \\ distr \ (x, Left \ y) = Left \ (x, y) \\ distr \ (x, Right \ y) = Right \ (x, y) \) | \(a \times ( b + c) = a \times b + a \times c \) |
プログラムで示すと以下のようになる。
distr :: (a, Either b c) -> Either (a, b) (a, c) distr (x, Left y) = Left (x, y) distr (x, Right y) = Right (x, y)
実行してみよう
*Main> let a = 3 *Main> let b = Left 4 *Main> let c = Right 5 *Main> distr (a, b) Left (3,4) *Main> distr (a, c) Right (3,5)
4) Haskellのデータ型の定義
Haskellでは、プログラマが新しいデータ型を作成することを許している。\(data\)というキーワードの後に型コンストラクタを書く。その後、\(=\)を書き、それに続けて値コンストラクタを記述する。例えば、\(x,y\)座標の点を表したいときは、
Prelude> data Point = P Float Float
とする。\(a=(3.1, 2.5)\)および\(b=(5.6, -2.4)\)を作りたいのであれば次のようにする。
Prelude> let a = P 3.1 2.5 Prelude> let b = P 5.6 (-2.4) Prelude> :t a a :: Point Prelude> :t b b :: Point
あるいはレコードを用いて次のようにも定義できる。
Prelude> data Point = P {x::Float, y::Float} deriving (Eq, Show, Read) Prelude> let a = P {x=3.1, y=2.5} Prelude> let b = P {x=5.6, y=(-2.4)} Prelude> :t a a :: Point Prelude> :t b b :: Point
5) 代数方程式からのデータ型の定義
さて、今回のメインディッシュである代数的データ型の話に移ろう。
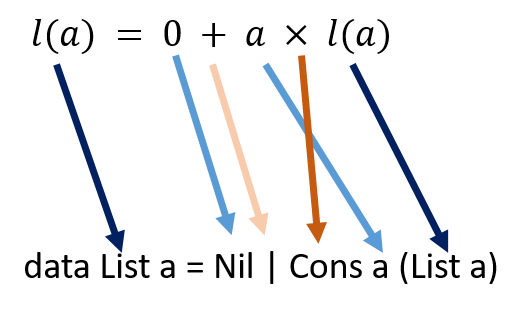
\(l(a) = 1 + a \times l(a) \)という代数方程式を考えよう。
これは、\(l(a) = \frac{1}{1-a} \)となるので、
\(l(a) = \sum_{i=0}^{\infty} a^i = 1 + a + a^2 + a^3 + a^4...\)
を得る(これは良く知られた公式であるが、実際に求めたければ、割り算をするとよい)。
これは、加算と乗算の形で表されているが、まず、\(a\)のべき乗のところを、1が()になることに注意して、タプルに代えてみよう。
\(l(a) = () + a + (a,a) + (a,a,a) + (a,a,a,a) + ...\)
次に、+の部分を\(Either\)で変えてみよう。
\(l(a) = Either \ () \ (Either \ a \ (Either \ (a,a) \ (Either \ (a,a,a) \ (Either \ (a,a,a,a)....\)
なんと、上の式は全てのタプルを表している(但し、後で説明するが、構成要素のデータ型は同じである)。
ところで、上の式で用いられている\(a\)について若干説明する。ここでの\(a\)は型変数と呼ばれるものである。データ型には、\(Int, Float, Char, Tuple\)など、あるいは自身で作ったものもあるが、型変数は、データ型を値とする変数である。従って、\(a=Int\)であれば、\((a,a,a)\)は\((Int,Int,Int)\)となり、整数を三つ組みとするタプルである。また、\(a=String\)であれば、文字列を三つ組みとするタプルである。
さて、\(l(a) = 1 + a \times l(a) \)は型変数\(a\)で作られるデータ型の構造を示す代数方程式と思うことにしよう。左辺の方はデータ型を示し、右辺の方はデータ型の作り方を示しているものとする。
\(l(a)\)は型変数を\(a\)を有するデータ型Listとしよう。即ち、Listは型コンストラクタである。
data List a
右辺の\(+\)は\(Either\)の英語での意味、即ちどちらかであるということにする。そして、記号は、\(|\)を用いる。また、1と\(a \times l(a)\)はタプルで取りあえず表してみよう。即ち、()と\( (a, l(a) )\)とにする。さて、タプルを新しいコンストラクタで置き換えることにする。()は値コンストラクタ\( N il \)で、また、\( (a, l(a) )\)は値コンストラクタ\(Cons\)で置き換える。このようにすると、後者の方は \(Cons \ a \ List(a) \)で表すことができる。即ち、代数方程式\(l(a) = 1 + a \times l(a) \)は、次のデータ型で置き換えることができる。
data List a = Nil | Cons a (List a)
上記のデータ型は、代数方程式から導き出されている。そこで、このようなデータ型を、特に、代数的データ型と呼ぶ。上記のデータ型は、また、良く知られているリストの定義である。下図に示すように、リストの定義が代数方程式から導き出される。何とも面白い変換だと思う。
圏論では、同じ構造の圏であれば、一方の圏の性質を他方の圏を用いて調べることができる。この役割をしてくれるのが関手(functor)である。これについては次回で述べる。