アントレプレナー(entrepreneur)は、元々は、フランス語である(フランス語での発音はアントルプルヌール、古いフランス語ではentreprendre)。企業家、実業家と訳されることが多いが、その語源はenとghendで、enはbetweenを、ghendはtakeを意味する。日本語に直訳すると間を取る人となる。
ペゾスが目指したのは、書店と読者の間に入り込んで、世の中にある本ならどのようなものでも安い価格で読者に提供することであった。アントレプレナーの意味を語源にさかのぼってみると、その位置づけが良くわかる。
オンライン書店に成功したペゾスは、本をもっと読みやすくするために、電子書籍の世界を確立しようとする。電子書籍のアイデアではソニーが先行していたのだが、品ぞろえができなかった(コンテンツを重視していたソニーがこの分野ではその重要性を十分に理解していなかった)。一方、キンドル発表前のペゾスの行動は、織田信長を超えるようなすさまじさで、全ては顧客のためにということで、出版社を恐怖の世界に陥れながら、電子書籍を用意していく。出版社と読者の間に入って、グーテンベルグ以来の活版印刷の世界をひっくり返してやるというなんともすさまじい行動であった。
電子書籍の普及のおかげで私もかなりの恩恵を受けている。今では、何百冊もの本がクラウドに蓄積されている。しかし、遅れている面もあって、まだ、たくさんの本が書棚を埋めている。それでも、これらの本もやがて電子書籍で置き換わり、近藤麻理恵さんの片付け術を用いなくても、部屋はすっきりするだろう。ペゾスにはとても感謝している。
しかし、アマゾンのクラウドに置かれる書籍が増えれば増えるほど、不安を感じるようになってきた。企業の寿命は30年という話もある。あれほど隆盛を誇った日本の電機メーカーもかつての勢いはない。アマゾンが、もし、うまくいかなくなった時、恐らくは千冊を超えているであろう書籍が一瞬のうちに消えてしまうというリスクから免れることができない。アマゾンが強くなれば強くなるほどリスクの度合いは強くなる。この時、アマゾンと読者の間に入ってリスクを回避してくれる新たなアントレプレナーが期待される(クリステンセンは、このような状況をイノベーションのジレンマと説明している)。
ペゾスが一番落胆するのは、作者が、直接、読者に本を渡すことだろう。しかも、ただで。このブログもそのような面を持っていると考えると、世の中は廻りまわっているとしか思えない。
ぎっくり腰、だいぶ良くなってきたが、再発しないように、少しだけ、記事を進める。
5 \(m\)要素の対象からn要素の対象への写像
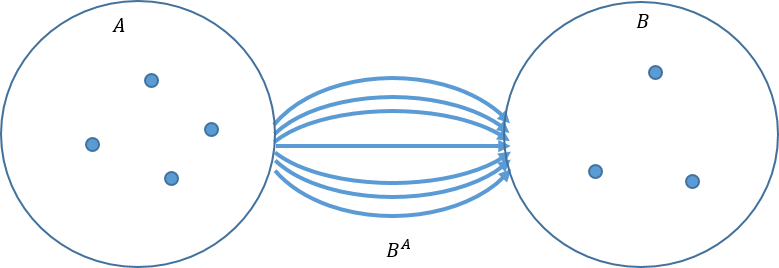
これまで、終対象、二要素、三要素の対象から、圏への写像を考えてきたが、これを一般化すると、\(m\)要素の対象\(A\)から圏\(B\)への写像ということになる。今、圏の方を\(n\)個の要素で構成される集合を対象としたものとする。この時、\(m\)要素の対象\(A\)から\(n\)要素の対象\(B\)への写像となる。写像の総数は\(n^m\)である。また写像の集合を\(B^A\)で表すことにする。
二つの集合の空間\(A\)と\(X\)があったとし、\(A \times X\)から別の集合の空間\(B\)への写像を\(f: A \times X \rightarrow B\)とする。写像\(f\)は二変数の関数であるが、これをカリー化して、一変数の関数\(f_a : X \rightarrow B \)とする。

カリー化関数\(f_a\)は、対象\(A\)から対象\(B\)への写像の集合の一つの要素と考えることができる。従って、集合\(B^A\)の中から、カリー化関数\(f_a\)を取り出せし、\(a \in A\)を与えれば\(b \in B\)が定まる。これは、\(B^A \times A\)から\(B\)への写像である。

いま、集合間\(A,B\)の写像の集合を\({\rm Hom}(A,B)\)で表す。空間\(A,X\)から空間\(B\)への写像の集合は\({\rm Hom}(X \times A ,B)\)となる。また、カリー化したときは\({\rm Hom}(B^A \times A,B)\)となる。これを可換図式で示したのが下図である。

これまでの説明は、対象を集合としたが、これを一般化するとデカルト閉圏へと導くことができる。