7.3 写像対象とは
ここでは写像対象を定義することにしよう。前回の記事で写像対象を説明するための図として下図を提示した。

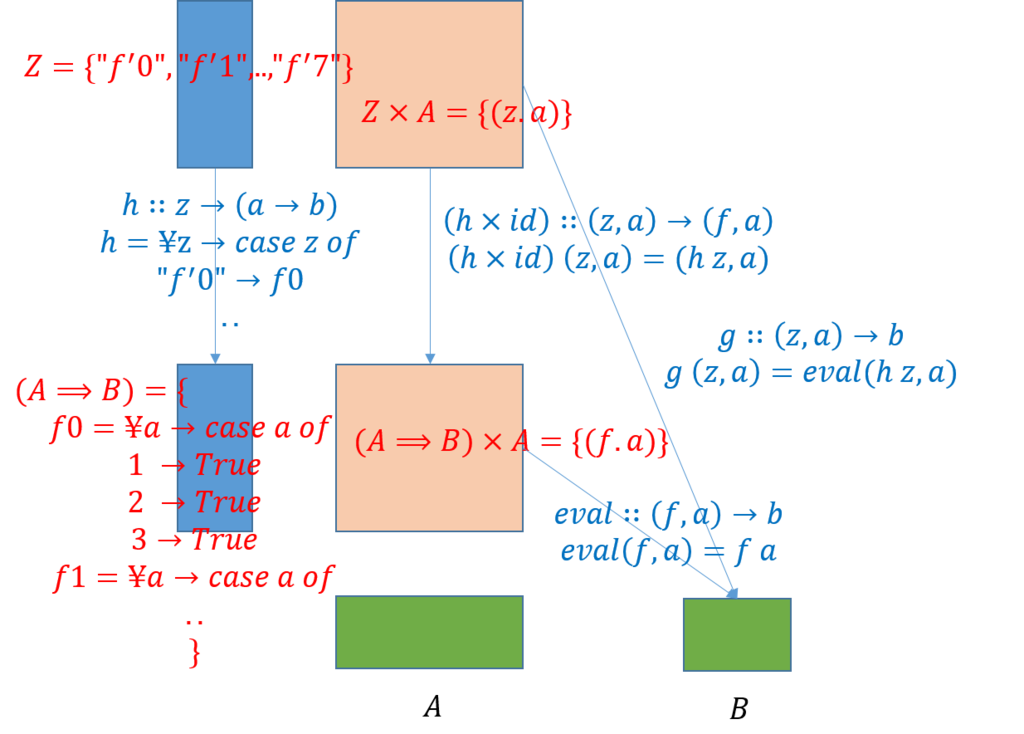
上図で、\(Z\)は最善の表現であるとすると、これは\(A\)から\(B\)への可能な写像を重なることなくすべてを含むような関数の集合であった。これは、\(A\)と\(B\)が定まれば一意に決まるので、\(A \Rightarrow B\)と表すことにしよう。\(A \Rightarrow B\)を縦方向に、\(A\)を横方向にして、その中央には、\((A \Rightarrow B) \times A\)の値を計算する関数を定義する(先の記事ではこれを表で表したが、より、一般的にするため関数とした)。この関数は一意的に定まるので\(eval\)で表す。即ち、上記の図で、\(Z\)は\(A \Rightarrow B\)で表し、\(g\)を\(eval\)で表す。そして、\(Z\)と\(g\)が空席になったので、\(Z’\)は\(Z\)で\(g’\)は\(g\)で書き換えると、下記の可換図式を得る。

この図で、\(A \Rightarrow B\)は関数の集合である。このため、これは対象とみなすことができる。そこで、これを関数対象と呼ぶことにする。なお、上の図が可換図式であることから、\(g\)には次のことが成り立つことが分かる。
\begin{eqnarray}
g = eval \circ (h \times id)
\end{eqnarray}
である。
そこで、上記の可換図式を圏として表しておこう。
①対象:\(A\), \(B\), \(Z\), \(A \Rightarrow B\), \(Z \times A\), \((A \Rightarrow B) \times A\)
②射:\(h\), \(h \times id\), \(g\), \(eval\)
③ドメイン、コドメイン:\(h : Z\rightarrow A \Rightarrow B\), \(h \times id : Z \times A \rightarrow (A \Rightarrow B) \times A \), \(g : Z \times A \rightarrow B\), \(eval : (A \Rightarrow B) \times A \rightarrow B\)
④恒等射:\(id_A\), \(id_B\), \(id_Z\), \(id_{A \Rightarrow B}\), \(id_{Z \times A}\), \(id_{(A \Rightarrow B) \times A}\)
⑤合成:\(g=eval \circ (h \times id)\)
また、結合律、単位律が成り立っていることは明らかである。
これで、\(A\)から\(B\)への関数の集合を写像対象として圏として表すことができた。
7.4 Haskellで表すための準備
ここで、対象\(Z\)から関数対象\(A \Rightarrow B\)への射(\(h\)をHaskellの型シグネチャを用いて表すことを考えよう。Haskellでは対象は型(Type)タイプで、射は関数で表す。型シグネチャは関数に入力される型と出力される型を示す。
型が分かっているときは大文字で表される型コンストラクタを用いる(例えば、整数という型であればInt)。また、型がその関数が利用される環境によって決まるときは小文字の型変数を用いる。例えば、2入力、1出力の関数\(f\)の型シグネチャは\(f :: (a, b) \rightarrow c\)で表される。ここで、\(a,b\)が入力、\(c\)が出力である。しかし、入力あるいは出力の中で、型が同じものについては、同じ型変数を用いる。例えば、上記で、2入力、1出力とも同じ型の場合には\(f :: (a, a) \rightarrow a\)とかく。
Haskellでは、関数は関数を入力とすることもできる。今、\(f\)が、1入力1出力の関数を入力するとき、\((a \rightarrow b) \rightarrow a \rightarrow c\)となる。この時、\((a \rightarrow b) \)は入力される関数となり、その次の\(a\)はこの関数への入力である。そして、最後の\(c\)は\(f\)の出力である。なお、型が同じ場合には型変数も同じにするのは前と同じである。
簡単な例を示そう。次のプログラムでは、関数\(dbl\)は関数\(f\)によって得られた値を倍にする。
dbl :: (Num b) => (a -> b) -> a -> b dbl f a = f a * 2
実行してみよう。
Prelude> :load "dbl.hs" [1 of 1] Compiling Main ( dbl.hs, interpreted ) Ok, modules loaded: Main. *Main> dbl length "abc" 6 *Main> dbl sin 5 -1.917848549326277 *Main> dbl sqrt 4 4.0
ある実数の2乗を出力する関数\(f\)を定義してみよう。
f :: Floating a => (a -> a) f = \x -> x ** 2
これを実行してみよう。
Prelude> :load "outputFunction.hs" [1 of 1] Compiling Main ( outputFunction.hs, interpreted ) Ok, modules loaded: Main. *Main> f 2 4.0 *Main> f 5 25.0 *Main> f 3.4 11.559999999999999 *Main> f (-2.6) 6.760000000000001
二つの数を入力し、その積をを出力する関数\(g\)を定義してみよう。
g :: Num a => ((a, a) -> a) g = \ (x, y) -> x * y
これを実行してみよう。
*Main> g (3,4) 12 *Main> g (3.5, 7.8) 27.3 *Main> g (-3.6, -2.5) 9.0
このように、関数の入出力で関数を用いているとき、入出力で用いられている関数は写像対象である。
7.5 写像対象をHaskellで表す
関数の入出力に関数を用いることを学んだので、写像対象の可換図式に現れた射\(h\),\(g\)をHaskellの型シグネチャで表すと次のようになる。
h :: z -> (a -> b) g :: (z,a) -> b
それでは、関数対象\(A \Rightarrow B\)を定義してみよう。ここでは、前回の記事で説明した例を用いる。例では、\(A\)は\(\{1,2,3\}\)は\(B\)は\(\{T,F\}\)であった。そこで、写像対象\(A \Rightarrow B\)は\(A\)から\(B\)への関数をすべて定義すればよいので、Haskellで表すと次のようになる。
f0 = \a -> case a of 1 -> True 2 -> True 3 -> True _ -> error "Not Assigned." f1 = \a -> case a of 1 -> True 2 -> True 3 -> False _ -> error "Not Assigned." f2 = \a -> case a of 1 -> True 2 -> False 3 -> True _ -> error "Not Assigned." f3 = \a -> case a of 1 -> True 2 -> False 3 -> False _ -> error "Not Assigned." f4 = \a -> case a of 1 -> False 2 -> True 3 -> True _ -> error "Not Assigned." f5 = \a -> case a of 1 -> False 2 -> True 3 -> False _ -> error "Not Assigned." f6 = \a -> case a of 1 -> False 2 -> False 3 -> True _ -> error "Not Assigned." f7 = \a -> case a of 1 -> False 2 -> False 3 -> False _ -> error "Not Assigned."
次に、\(Z\)を定義しよう。これは、前回の例では以下の関数を表すものであった(但し、\(Z'\)は\(Z\)に変えてある)。

そこで、対象\(Z\)は関数の名前の集合としよう。即ち、\(Z=\{“f’0”, “f’1”, “f’2”, “f’3”, “f’4”, “f’5”, “f’6”\}\)
次に、\(H:Z \rightarrow (A \Rightarrow B) \)を定義しよう。次のようになる。
h = \z -> case z of "f'0" -> f0 "f'1" -> f1 "f'2" -> f2 "f'3" -> f3 "f'4" -> f4 "f'5" -> f4 "f'6" -> f6 _ -> error "Not Assigned."
さらに、\(g : Z \times A -> B\)を定義しよう。\(g = eval \circ (h \times id)\)より、次のようになる。
g (z, a) = eval (h z, a) eval (f, a) = f a
可換図式をHaskellで表すと次のようになる。
それでは実行してみよう。
Prelude> :load "fObject.hs" [1 of 1] Compiling Main ( fObject.hs, interpreted ) Ok, modules loaded: Main. *Main> g ("f'0", 1) True *Main> g ("f'0", 2) True *Main> g ("f'0", 3) True *Main> g ("f'1", 1) True *Main> g ("f'1", 2) True *Main> g ("f'1", 3) False *Main> g ("f'1", 4) *** Exception: Not Assigned. CallStack (from HasCallStack): error, called at fObject.hs:10:19 in main:Main *Main> g ("f'2", 3) True *Main> g ("f'3", 1) True *Main> g ("f'4", 1) False *Main> g ("f'7", 2) *** Exception: Not Assigned. CallStack (from HasCallStack): error, called at fObject.hs:50:19 in main:Main
思い通りに機能していることが分かった。
7.5 カリー化とアンカリー化
入出力に関数を用いることを学んだが、関数は一般に\(n\)変数である。そこで、\(n\)変数の関数をそれより一つ少ない変数の関数に次のように変えることをカリー化という。即ち、最初の変数を変数とする関数の戻り値を関数として、これが残りの変数を受けて元の関数と同じ値を返すようにすることをカリー化という。いま、\(f : A_0 \times A_1 \times, ..,\times A_n \rightarrow B\) とした時、\(g : A_0 \rightarrow h\), \(h : A_1 \times A_2 \times, ..,\times A_n \rightarrow B\)となるとき、\(h\)は\(f\)をカリー化した関数と呼ばれる。 また、その逆はアンカリー化という。
カリー化とアンカリー化の例として、ここでは、2変数の関数を1変数の関数に、1変数の関数を2変数の関数に、変えることを考えよう。これを、再帰的に利用すれば、カリー化とアンカリー化を一般化できる。定義に従えば、カリー化\(curry'\)とアンカリー化\(uncurry'\)の関数は次のように定義できる。
curry' :: ((a, b) -> c) -> (a -> (b -> c)) curry' f = \ a -> (\ b -> f(a,b)) uncurry' :: (a -> (b -> c)) -> ((a, b) -> c) uncurry' f = \ (a,b) -> (f a) b
\(curry'\)の定義は次のようになっている。入力が2変数\((a,b)\)出力が\(c\)である関数は、入力\(a\)を受けて、入力が\(b\)で出力が\(c\)の関数を出力する。
それでは、利用してみよう。長方形の面積を求める2入力の\(area\)という関数を定義する。そして、カリー化したときの型シグネチャを求めてみよう。
Prelude> :load "curry.hs" [1 of 1] Compiling Main ( curry.hs, interpreted ) Ok, modules loaded: Main. *Main> area (a,b) = a * b *Main> :t curry area curry area :: Num c => c -> c -> c
カリー化した時の型シグネチャは \(Num c => c -> c -> c\)となっている。これは、実は\(Num c => c -> (c -> c)\)と同じである。後者の\(Num c => c -> (c -> c)\)では、最初のタイプ\(c\)の入力を与えると、関数\((c -> c)\)を得る。この関数はタイプ\(c\)の入力を与えると出力\(c\)を得ることを意味する。前者の\(Num c => c -> c -> c\)では、タイプ\(c\)の入力を与えた後で、タイプ\(c\)の入力を与えるとタイプ\(c\)の出力を得ることを意味する。従って、全者と後者は同じである。従って、期待通りにカリー化されていることが分かる。そこで、計算を実行してみよう。
*Main> area (3,4) 12 *Main> curry area 3 4 12
カリー化は、ざっくばらんにいうと、多変数の入力をバラバラにして入力することとなる。
それでは、アンカリー化についても調べてみよう。同じように、面積を求める関数area'を次のように定義する。
*Main> area' a b = a * b *Main> :t uncurry area' uncurry area' :: Num c => (c, c) -> c
\(area'\)の定義は、\(area' a b\) は\(area' a\)を実行して関数を得て、この関数に\(b\)を与えて面積を求めることと同じである。即ち、次のように定義しても同じである。
*Main> (area' a) b = a * b
\(area'\)をアンカリー化すると、\((c,c) -> c\)の2入力関数が得られることが分かる。
そこで、これを実行する。
*Main> area' 3 4 12 *Main> uncurry area' (3,4) 12
期待通りになっていることが分かる。