しばらく休みを頂いたが、この間、古代史の関係の書物を読み漁った。特に、松木武彦さんの本が気に入った。
『美の考古学:古代人は何に魅せられてきたか』と『旧石器・縄文・弥生・古墳時代 列島創世記』を、また、共著だが『弥生時代って、どんな時代だったのか?』を楽しく読むことができた。日本列島の古代を知ろうとすると、中国に残されているわずかなものを除くと全く文字資料がないため、考古学的な遺跡を頼りに解明するしかない。しかし、どこそこでどのような土器が発見されたとか、どのようなタイプの墓が発見されたのかということを述べるだけでは、この時代に人々がどのように生活していたのかを伝えてはくれない。そこで、松木さんは認知考古学を導入することで、この時代の人がどのように考えて、土器や住居や墓を作ったのかを説明してくれる。無機的な世界に息吹を与えてくれ、歴史を楽しく知ることができる。

認知考古学の系統を手繰っていくと、英国のスティーブ・ミズン(Steven Mithen)というレディング大学(University of Reading)の教授にたどり着く。彼は『心の先史時代(The Prehistory of the Mind)』、『氷河期以降(After the Ice: A Global Human History)』という本を書いている。前者はまだ読んでいないのでその内容は説明できないが、後者の本では紀元前2万年から5千年までの時代を変わったスタイルで描いている。ラボック君に世界中を旅をさせ、見聞きしたことを伝えるという手法で歴史を語らせる。もちろん、縄文時代の日本列島も訪問する。最初に降り立つのは、桜島近くの上野原遺跡だ。歯が一本もない少し年老いた女性が縄文土器を作り出す様子などを説明してくれる。上野原遺跡で発見された土器などを元に認知考古学を用いてその当時の生活を描き出してくれる。点と点のつながりでしかなかった古代の遺物がビジュアルにつながり読む人を楽しませてくれる。

英国には別のアプローチをとる考古学者もいる。コリン・レンフルー(Colin Renfrew)だ。彼はケンブリッジ大学の教授を務めた。『先史時代と心の進化(Prehistory: The Making of the Human Mind)』、『考古学―理論・方法・実践 (Archaeology: Theories, Methods, and Practice)』を著作している。人類の進歩には2段階あって、遺伝子が進化した時代と、共通の知識の蓄積により変化した時代とがあると説明している。人類がアフリカを出る6万年前には、遺伝子的な進化は終了し、現代人と同じ遺伝子を有していたと述べている。アフリカを出た後、それぞれの地域によって異なる文化を築いたのは、共通知識の蓄積の仕方が異なったためだと説明している。

認知考古学の助けを借りて文字がなかった時代を読み解くという方法は、圏論での関手を利用してある圏から別の圏を覗くいう方法と重なり合い、興味深かった。
他にもうひとつ面白い本があったのでそれも紹介しておこう。ここ数十年の考古学の研究の新しい流れの中で、最新技術が考古学に応用されている。その結果、これまでとは異なる見解が多く示されこともある。特に、放射性炭素14年代測定法やDNAの解読などの寄与は大きい。斎藤成也の『日本列島人の歴史』は、中学生・高校生でも楽に読めるように書かれている良書である。現代から古代の方に歴史を逆にたどっていき、最後に彼が主張する「三段階渡来モデル」の説明がある。DNAの解析結果をベースとしているので、説得力のある理論だと思う。

7 写像対象
これらの理論に圏論を応用できないかと考えているのだが、まだ、そこまでの準備はできていない。さて、前振りが長くなったが、これから、圏論の中でも面白い分野に属する写像対象(functional object, map object)について説明しよう。写像対象は指数対象(exponential object)とも呼ばれる。
7.1 集合と関数
ここから読み始める人もいると思うので、これまでの説明を前提にしないでも、理解できるように説明する。圏は、5つの構成要件と2つの条件により定義されている。その中で、重要な構成要件は対象(objects))と射(morphismsまたはarrows)の二つである。集合(Sets)と関数(functions)を圏として表そうとすると、集合を対象として表すことができ、関数は射として表すことができる。
ここからしばらくは、圏論の世界を離れて集合と関数の世界で話をすることにしよう。
集合と関数の関係は次のように決められている。関数\(f\)はある集合\(A\)からある集合\(B\)への方向性のある対応関係を与える。そして、一つの制約がある。それは、\(A\)の全ての要素\(a\)に対して、\(B\)のある要素\(b\)が対応しなければならない。但し、\(B\)の全ての要素\(b\)に対しては対応する\(A\)の要素がなくても構わない。即ち、関数\(f:A \rightarrow B\)は次の条件を満足するものである。
\begin{eqnarray}
\forall a \in A, \exists b \in B, b = f(a)
\end{eqnarray}
\(A\)から\(B\)への関数を定義することができる(この時、\(A\)をドメイン、\(B\)をコドメインと呼ぶ)。例えば、\(A\)は\(\{1,2,3\}\)という3つの数字の集まりで、\(B\)は\(\{T,F\}\)はブール値であるとすると、可能な関数は下図に示すように8つである。

7.2 関数の集合
集合と関数を圏として表す時の最も自然な方法は、集合を対象に、関数を射とすることである。先ほどの例では、圏\(\mathcal{C}\)において、対象の集まり(対象の類)\(ob(\mathcal{C})\)は\(\{A,B\}\)であり、射の集まり(射の類)\(\rm{Hom}(\mathcal{C})\)は\(\{f_0,f_1,f_2,f_3,f_4,f_5,f_6,f_7\}\)である。圏として完成させるためには、この後の作業として、恒等射(\(id_A:A \rightarrow A,id_B:B \rightarrow B\))、射の合成(\(\circ\))を定め、結合律、単位律(\(id_A \circ f_i = f_i,f_i \circ id_B=f_i\)である。但し、\(i=0..7\))が成り立つようにすればよい。
集合と関数を圏として表す方法は一つではない。先の例で、\(A\)から\(B\)への関数を数え上げた。\(A\)から\(B\)への関数の集まりを集合と見なすと対象にできるのではと考えても不思議ではない。そこで、関数の集まりを\(Z=\{f_0,f_1,f_2,f_3,f_4,f_5,f_6,f_7\}\)とし、以下のように縦方向に\(Z\)を横方向を\(A\)を配置し、交わったところを\(B\)即ち\(b=f_i(a)\)となるようにして、表を作成してみよう。

どこかで見たような表ではないだろうか。そう、デカルト積だ。デカルト積は圏として表すことができる。それは圏の積と呼ばれる。積の圏では、二つの対象が存在し、さらにその二つの対象の積も対象になる。今説明している例では、\(A\)と\(Z\)とさらにその積の\(Z \times A\)である。
積の圏はさらに\(Z \times A\)と性質を同じにする対象\(C\)を有する。数学的な説明でないが、\(Z \times A\)は最善の表現であり\(C\)はそれより劣った表現である。\(Z \times A\)はしばしば極限といわれる。極限とは何を表しているのだろう。\(\times\)は論理積を意味するときがある。\(Z \land A\)と考えると\(A\)と\(Z\)の共通部分だ。最善な共通部分とは、余すところなく共通部分を拾ったものだろう。それより劣る表現は共通部分の一部分を表したものだろう。あるいは、共通部分を二重に表現したものも劣る表現であろう(これはすぐ後で説明するが共通部分への写像が選択になるので最善とは言えなくなる)。このようなことを考えると、\(A\)と\(Z\)が整数である時、\(\times\)が共通に含まれる素数ということを表しているものと理解すると、最善な表現は最大公約数となる。そして、積の圏の場合には、\(\times\)は\(A\)から\(B\)への写像を表しているので、最善の表現は無駄のない余すことのない写像の集まりになるだろう。このように理解して次に進もう。
数学的な厳密さを用いて説明しよう(下図参照)。積の圏で\(Z \times A\)が最善の表現であるとは、どのような\(C\)を持ってきたとしても、\(C\)から\(Z \times A\)への変換\(u\)は一意に定まり、\(C\)から\(Z\)への変換は\(p'=p \circ u\)で、\(C\)から\(A\)への変換は\(q'=q \circ u\)で与えられることをいう。但し、\(p:Z \times A \rightarrow Z, q:Z \times A \rightarrow A\)である。

次に、\(Z \times A\)と性質を同じにする対象\(C\)について話を進めよう。先の例では、\(A\)から\(B\)への写像を重複させるまたすべて含むような関数の集まりを求めた。そこで、今回は、\(A\)から\(B\)への写像をすべて含まなくてもよいし、重複してもよいということにしよう。このような関数の集まりを\(Z'\)とする。例えば、下図のようなものを作成したとする。
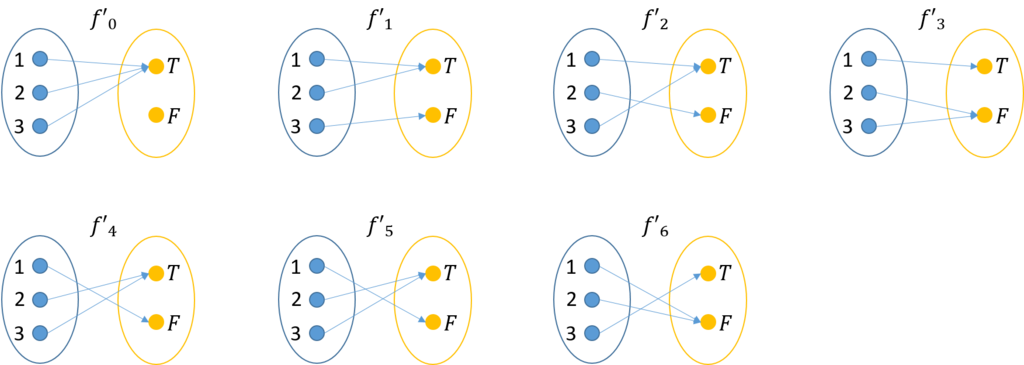
この関数の集まりを\(Z'=\{f'_0,f'_1,f'_2,f'_3,f'_4,f'_5,f'_6\}\)としよう。表を作成すると次のようになる。
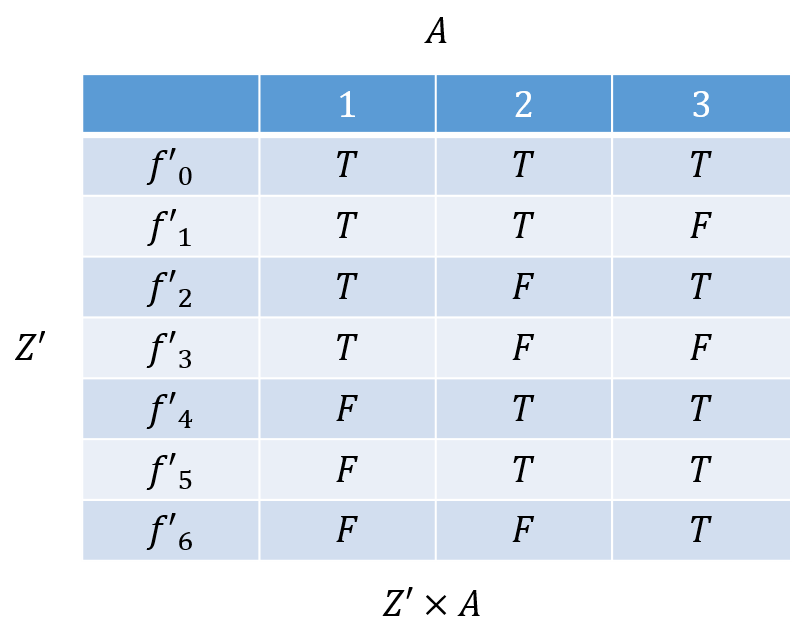
この例で、\(Z'\)から\(Z\)へは次のように変換することができる。
\begin{eqnarray}
f'_0 \rightarrow f_0 \\
f'_1 \rightarrow f_1 \\
f'_2 \rightarrow f_2 \\
f'_3 \rightarrow f_3 \\
f'_4 \rightarrow f_4 \\
f'_5 \rightarrow f_4 \\
f'_6 \rightarrow f_6 \\
\end{eqnarray}
この例に限ることなく、一般にどのような関数の集まり\(Z'\)が与えられたとしても、\(Z'\)から\(Z\)への写像\(h\)を一意に定めることができる。即ち、\(Z' \times A\)から\(Z \times A\)への写像\(u=(h \times id)\)を一意に定めることができる。

\(Z\)は特別な存在であった。即ち、これは\(A\)から\(B\)への写像を重複することなくすべてを含むような集まりであった。そしてどのような\(A\)から\(B\)への関数の集まりを持ってきたとしても\(Z'\)から\(Z\)への写像\(h\)を一意に定めることができる。積の圏では、先にも述べたが、このようなものを極限という。Milewskiの言葉を借りれば最善な表現(Best Representation)である。
しかし、可換図式を見て分かると思うが、恒等射\(id\)が多すぎてあまり面白くはない。そこで、次の節で述べる関数対象を扱えるようにするために、ドメインを対象として組込み、次の可換図式を用意する。

この図で、\(Z'\)が\(Z\)より劣る表現である時、\(Z'\)から\(Z\)へ一意に定まる関数\(h\)が存在する。また、いかなる\(Z'\)に対しても、\(Z'\)から\(Z\)へ一意に定まる関数が存在するとき、\(Z\)は最善の表現と呼ぶことにする。\(Z'\)が\(Z\)より劣る表現のとき、\(Z' \times A\)から\(Z \times A\)へ一意の関数\((h \times id)\)が存在する。そして、\(Z' \times A\)から\(B\)への関数を\(g'\)とし、\(Z \times A\)から\(B\)への関数を\(g\)としたとき、\(g'=g \circ (h \times id)\)である。
これで、関数の集合\(Z\)を対象として扱う準備ができたので、次はその役割について説明しよう。