bitterharvest’s diary

A Bitter Harvestは小説の題名。作者は豪州のPeter Yeldham。苦闘の末に勝ちえた偏見からの解放は命との引換になったという悲しい物語

関手ー双関手

プログラマーのための圏論 (初級編：圏論とHaskell)

６．５　双関手

１）関手としての積と余積

前々回の記事で、Haskellが用意している関手のリストを示した。

Prelude> :i Functor
class Functor (f :: * -> *) where
  fmap :: (a -> b) -> f a -> f b
  (<$) :: a -> f b -> f a
  {-# MINIMAL fmap #-}
  	-- Defined in ・eGHC.Base’
instance Functor (Either a) -- Defined in ‘Data.Either’
instance Functor [] -- Defined in ‘GHC.Base’
instance Functor Maybe -- Defined in ‘GHC.Base’
instance Functor IO -- Defined in ‘GHC.Base’
instance Functor ((->) r) -- Defined in ‘GHC.Base’
instance Functor ((,) a) -- Defined in ‘GHC.Base’

この中で、\( ((\rightarrow) r)\)については説明したが、\( ((,) a)\)と\( (Either \ a)\)については説明しなかった。これらは、圏論での積と余積についてのところで説明した。その時は、一つの圏の中での二つの対象と一つの対象の普遍的な関りを説明する中で述べた。

それでは積の方から説明を始めよう。Haskellでは積は\((a,b)\)と書かれる。常套手段だが、カンマを中置関数と見なして、これを前置関数にすると\((,) \ a \ b\)と書くことができる。このようにすると、\((,) \)は型コンストラクタと見なすことができる。あるいは、一つのデータ型を作り出しているといってよいであろう。データを取り出す手段が、\((,) \)である(同じようなことは関数すべてにいえる。関数は型コンストラクタで、データを取り出す手段である)。

\((,)\)が型コンストラクタであることから、これは関手として利用することが可能である。その例を下図に示す。
f:id:bitterharvest:20170222104958p:plain
ここで、(,)は次のように関手として定義されている。

Instance Functor ((,) a ) where
  fmap (x,y) = (x, f y)

また、Eitherは次のように定義されている。

Instance Functor ((,) a ) where
  fmap (x,y) = (x, f y)

２）関手としての積と余積

関手はある圏からある圏(同じ圏でも構わない)への写像であった。それでは、ドメインが一つの圏ではなくて、二つの圏の場合はどうであろうか。その例を示そう。
f:id:bitterharvest:20170222105012p:plain
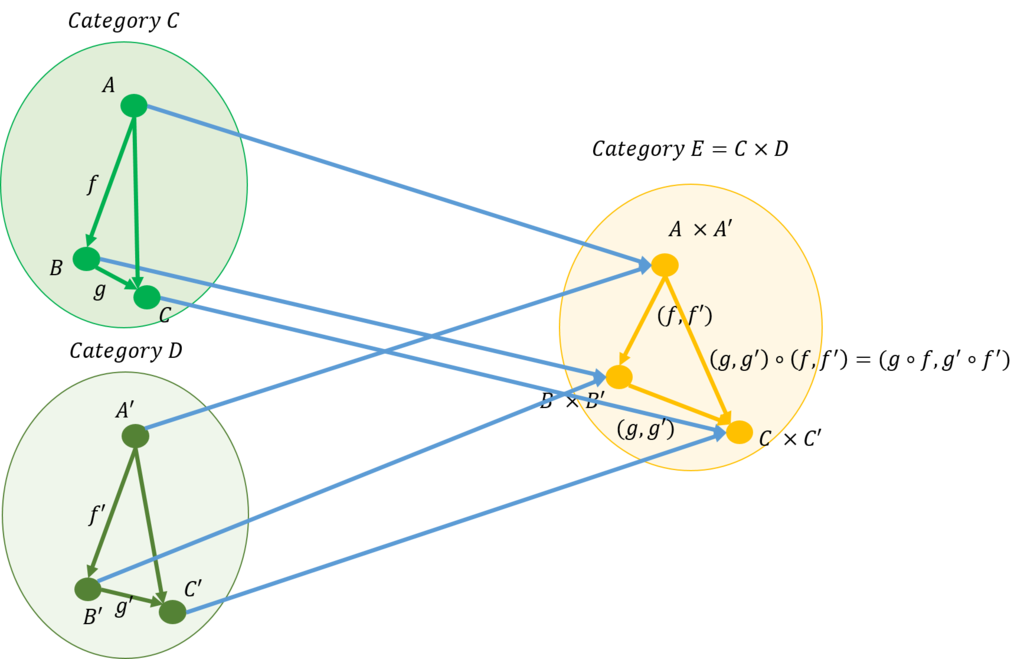
この図は、先に説明した積を一般化したものである。積のそれぞれは別々の圏に属す(図では\(\mathcal{C}\)と\(\mathcal{D}\)である)。それぞれから対象が選ばれ、それは別の圏へと写像される(図では\(\mathcal{E}\)である)。

一つの圏からではなく二つの圏(\(\mathcal{C,D}\))からひとつの圏(\(\mathcal{E}\))に写像しているような関手(\(F: \mathcal{C} \times \mathcal{D}\rightarrow \mathcal{E}\))を双関手(Bifunctor)という。これのHaskellでは次のように定義することができる。

class Bifunctor f where
  bifmap :: (a -> b) -> (a' -> b') -> (f a a' -> f b b')

積と余積はこのクラスのインスタンスとして定義することができる。下図には双関手と積の関係を示す。
f:id:bitterharvest:20170222104507p:plain

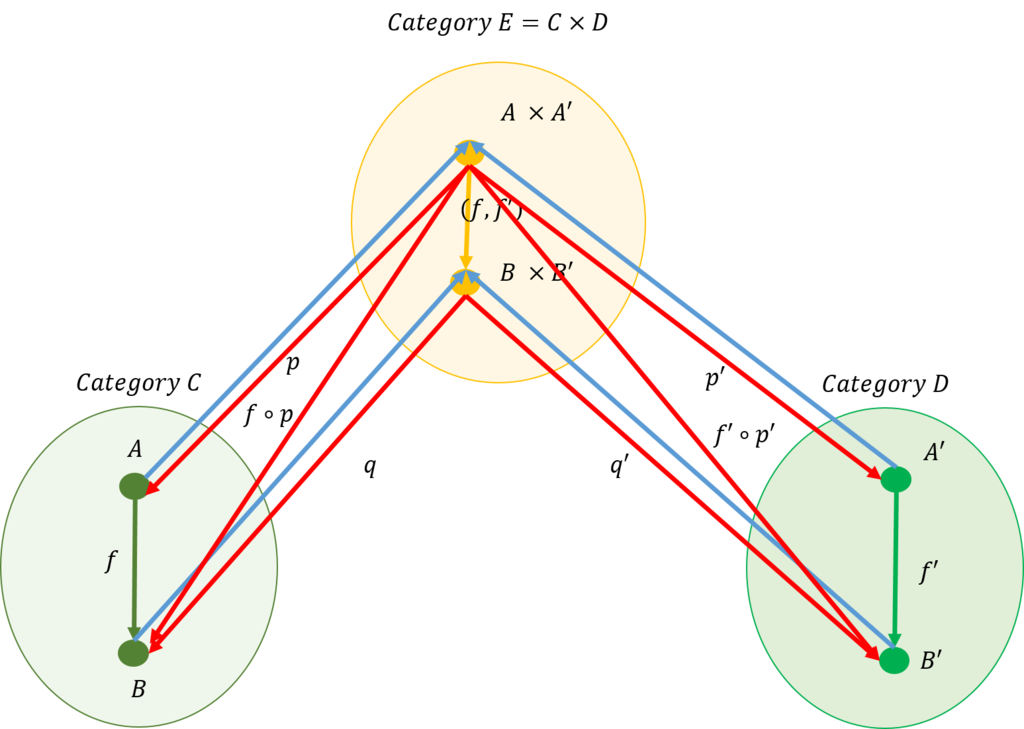
関手を学ぶ良い機会になるので、積と余積のインスタンスの作成は読者に任せる(双関手の実装はData.Bifunctorを調べると分かる)。

次回はモノイド圏についてである。