3.2 \(Reader\)を定義する
Haskellでは\(Reader\)を用意している。Control.Monad.Readerというモジュールを読み込めば、使えるようになっている。しかし、このモジュールを理解しようとすると、忍耐力を必要とする。汎用性を高めるために、\(Reader\)が、\(ReaderT\)と呼ばれるデータ型を利用して、定義されているためだ。このため、\(Reader\)を理解しようとすると、別のいくつかのことを理解しなければならない。この作業は、煩わしく、下手をすると、何を理解しようとしていたのかさえ忘れてしまう。
そこで、ここでは、\(Reader\)の理解を助けるために、Haskellでの定義から離れて、必要な事項だけで説明することとしよう。
前回の記事で、\(Reader\)は
type Reader u a
と理解して、利用した。これは、\(u\)という環境を与えて、\(a\)を出力するというものであった。\(Reader\)は、入力を\(u\)とし\(a\)を出力する関数を、データ型としたものと考えてよい(圏論では、データ型は対象である。関数を対象に選べるのも、圏論の汎用性、有用性を示す証左である)。そこで、次のように定義しよう。
data Reader u a = Reader (u -> a)
Haskellで用いられている用語の説明をしておこう。等式の左側に存在する\(Reader\)は型コンストラクタ(type constructor)と呼ばれる。また、\(u\)と\(a\)は型引数(type argument)と呼ばれる。\(data Reader \ u \ a\)により、データ型\(Reader\)は、データ型\(u\),\(a\)を用いて定義されていることを示す。
等式の右側の\(Reader\)は値コンストラクタ(value constructor)あるいはデータ・コンストラクタ(data constructor)と呼ばれる。これに続く\( \ u \rightarrow \ a\)は型と呼ばれる。そして、関数となっているので、特に、代数的データ型と呼ばれる。
上の定義を用いて、データ型\(Reader\)の値をいくつか求めて見よう。
Prelude> data Reader r a = Reader (u -> a) Prelude> a = Reader $ \u -> 0.5 * u -- 数値を入力し、その半分を求める関数。もちろんa = Reader (*0.5)と入力しても同じ Prelude> :t a a :: Fractional a => Reader a a Prelude> b = Reader $ \u -> show u – 数値などを入力し、その文字列を求める関数 Prelude> :t b b :: Show a => Reader a String Prelude> c = Reader $ \u -> show (u* u) – 数値を入力し、その2乗の文字列を求める関数 Prelude> :t c c :: (Show a, Num a) => Reader a String *Main> d :: Reader Int String ; d= Reader $ \u -> show ((*2) u) – 正数を入力し、その2倍の文字列を求める関数。これはd = Reader $ show . (*2)と同じ *Main> :t d d :: Reader Int String
1)ファンクタとしての定義
データ型が用意できたので、このデータ型を用いる関数を用意しよう。ファンクタから始めよう。
関手\(Reader\)は、与えられた関数を\(Reader\)というコンテナで包むものである。
データ型が用意できたので、このデータ型を用いる関数を用意しよう。ファンクタから始めよう。ファンクタでは、\(fmap \ f\)という関数を用意する必要がある。
圏\(\mathcal{C}\)は、関手\(Reader \)によって圏\(\mathcal{C’}\)に移されるものとしよう。そして、圏\(\mathcal{C}\)は、射の集まりで構成され、それらは\(U\)から\(X\)への射(\(r:U \rightarrow X\))としよう。また、任意の射\(r\)は、関手\(Reader\)によって圏\(\mathcal{C’}\)の射にコンテナをかぶせられた射\(Reader \ r\)に写されるものとしよう。
なお、コンテナをかぶせられた射は、関数\(runReader \ (Reader \ r) \ u\)を実行することにより、\(r(u)\)の値を出力する。
これらの関係を示すと下図になる。
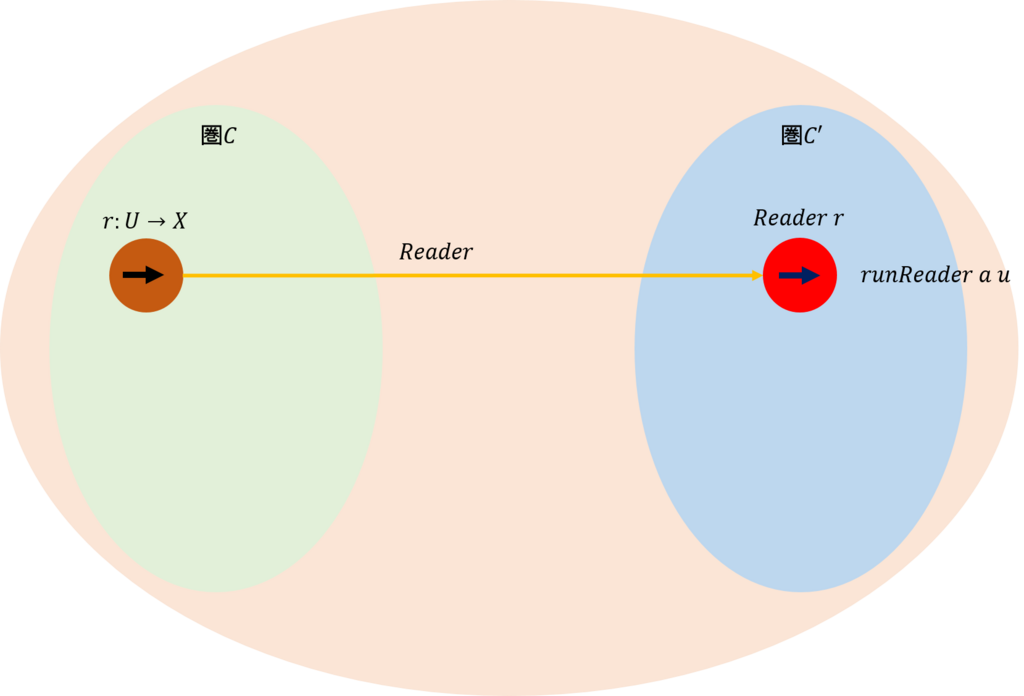
次に、圏\(\mathcal{C}\)内に別の射\(f\)が存在し、これは、射\(r\)を別の射\(s\)に写すものとする。このとき、\(s = f . r\)となる。また、\(f\)を関手\(Reader\)で写したものを\(fmap \ f\)としよう。これらから、次のような可換図式を得る。
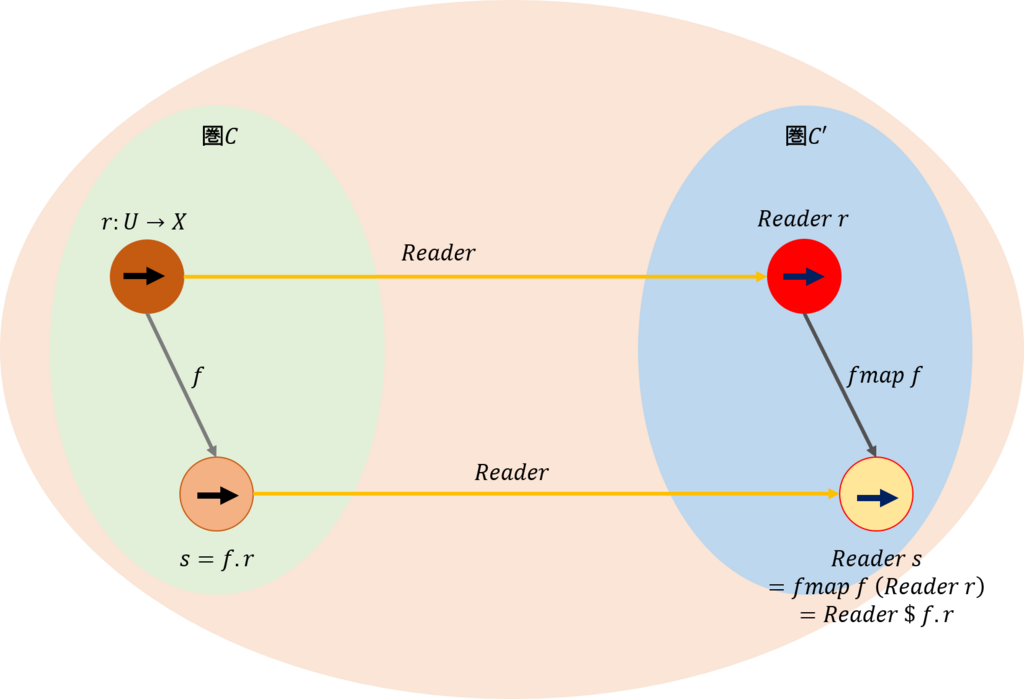
プログラムで示した例\(r =(*2),f=show\)の可換図式を求めると下図のようになる。
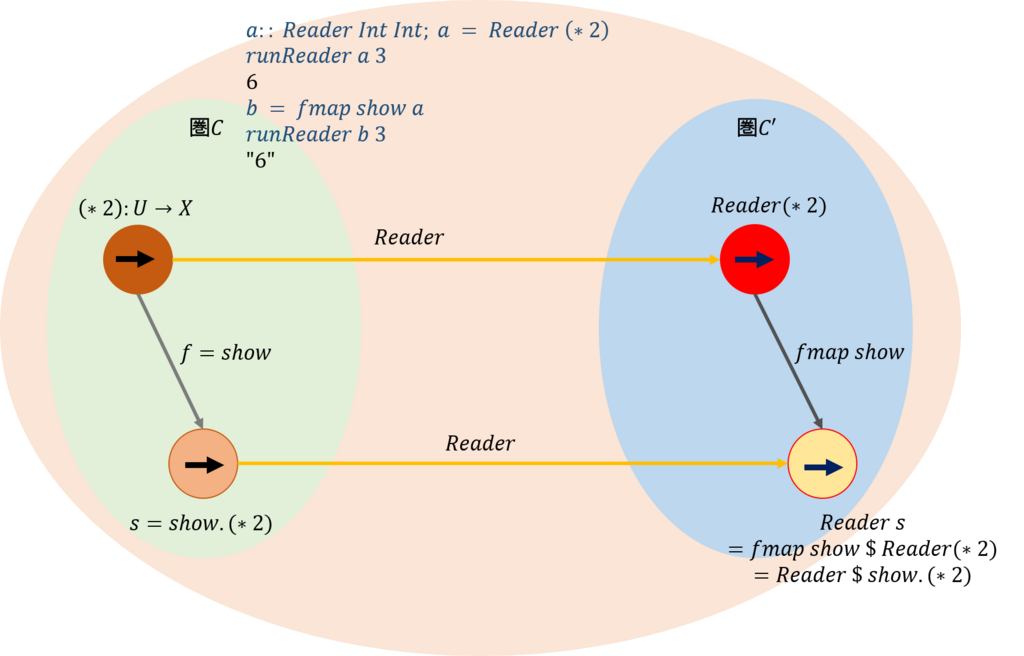
それでは、Haskellでのファンクタの定義を示そう。
instance Functor (Reader r) where fmap f (Reader r) = Reader $ f.r
なお、ファンクタとして定義するとき、\(Reader\)が関手なので、\(r\)をつけずに、
instance Functor Reader where fmap f (Reader r) = Reader $ f.r
と定義しそうになるが、\(fmap\)の定義において、\(Reader\)ではなく\(Reader \ r\)を用いる必要があるので、\(r\)をつけないと誤りとなる。
2)モナドとしての定義
次はモナドでの関数を定義しよう。本論に入る前に、モナドがどのような数学的な概念であったかを復習しておこう。モナドとは、ある圏\(\mathcal{C}\)のモナド\(M\)とは、\(\mathcal{C}\)の対象\(A\)をコンテナ\(M\)で包んだものであり、それは\(M \ A\)と記述される。モナドには2つの関数が用意されていて、一つはモナドを作り出すもの、他の一つは、モナドからモナドを作り出すものである。二つの関数の用意の仕方にはいろいろあるが、Haskellでは\(return\)と\((>>=)\)を用意することになっている。それでは、下図を用いながら説明しよう。
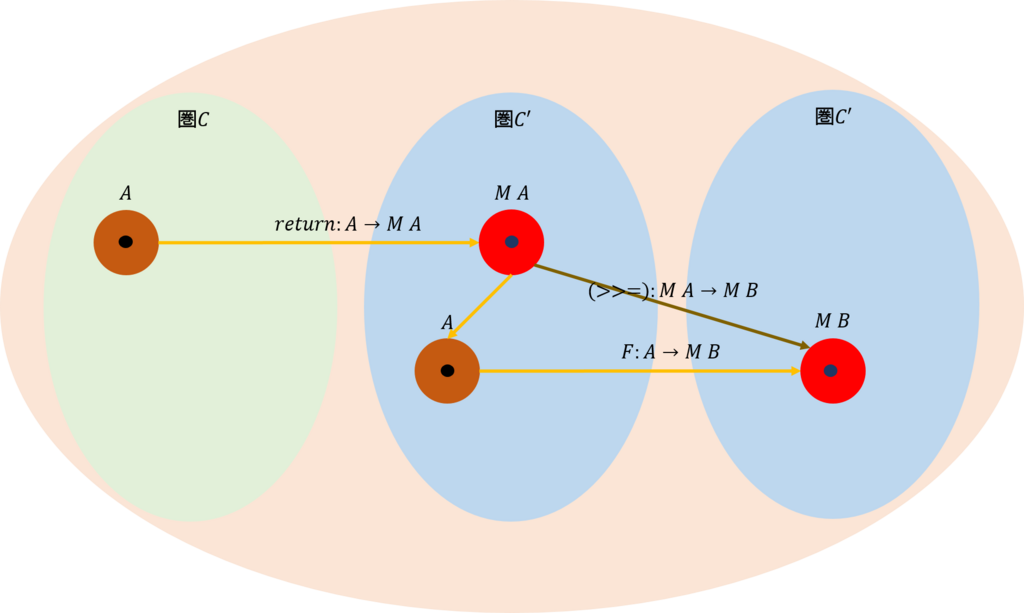
\(return\)は圏\(\mathcal{C}\)の対象\(A\)をモナドとしてのコンテナで包むことである。これを、\(return\)の型シグネチャで確認しよう。
:t return return :: Monad m => a -> m a
例をいくつか挙げておこう。[ ] はモナドなので、整数から各括弧の付いたモナドを作成してみよう。
Prelude> a = return 3 :: [Int] Prelude> a [3] Prelude> :t a a :: [Int]
\(Maybe\)もモナドなので、整数から\(Maybe\)のモナドを作成してみよう。
Prelude> b = return 3 :: Maybe Int Prelude> b Just 3 Prelude> :t b b :: Maybe Int
次の関数は、\((>>=)\)である。これは、二つの引数(\(M \ A,F\)))が与えられる。一つはモナドの値である。もう一つは関数である。この関数\(F\)は少し変わっていて、モナドにする前の値、即ちコンテナに包まれる前の値\(A\)を用いて、これをモナド\(M B\)に変換する。式で表すと、\(F: A \rightarrow M \ B\)である。型シグネチャで確認しておこう。
Prelude> :t (>>=) (>>=) :: Monad m => m a -> (a -> m b) -> m b
それでは、いくつかの例を見ていこう。まず各括弧の場合だ。\(f\)の関数は、整数が与えられたならば、それに4を加えて各括弧でくくることにしよう。次のようになる。
Prelude> a = return 3 :: [Int] Prelude> f = \r -> [r + 4] Prelude> c = a >>= f -- 中置関数として Prelude> c [7] Prelude> d = (>>=) a f -- 前置関数として Prelude> d [7]
次は\(maybe\)の例を示そう。整数が与えられた時、それを2倍にし、モナド\(Maybe\)にして返す関数を考えよう。
Prelude> a = return 3 :: Maybe Int Prelude> f = \x -> Just $ (*2) x Prelude> (>>=) a f Just 6
モナドに慣れてきたので、\(Reader\)に対しても、\(return\)と\((>>=)\)を定義することとしよう。
まず、\(return\)から始めよう。次のように定義されている。
return x = Reader $ \u -> x
上の定義では、\(u\)の値に関わらず、\(x\)の値が定まるので、\(\backslash u -> x\)は定数関数となる。
いくつかの例を挙げてみよう。 \(return\)で出力値を与えて、\(runReader\)で実行するだけの簡単なものだ。
*Main> a = return 3 :: Reader Int Int *Main> :t a a :: Reader Int Int *Main> runReader a 6 3 *Main> b = return 3 :: Reader String Int *Main> :t b b :: Reader String Int *Main> runReader b "Three" 3 *Main> c = return "Jack" :: Reader String String *Main> :t c c :: Reader String String *Main> runReader c "Betty" "Jack" *Main>
次は、\(>>=\)である。モナドでの定義は次のようになっている。
*Main> :t (>>=) (>>=) :: Monad m => m a -> (a -> m b) -> m b
これをReaderで置き換えると次のようになる。
*Main> :t (>>=) (>>=) :: Reader r -> return . s -> reader g
それでは、下図を参考にしながら、(>>=)を作成していこう。
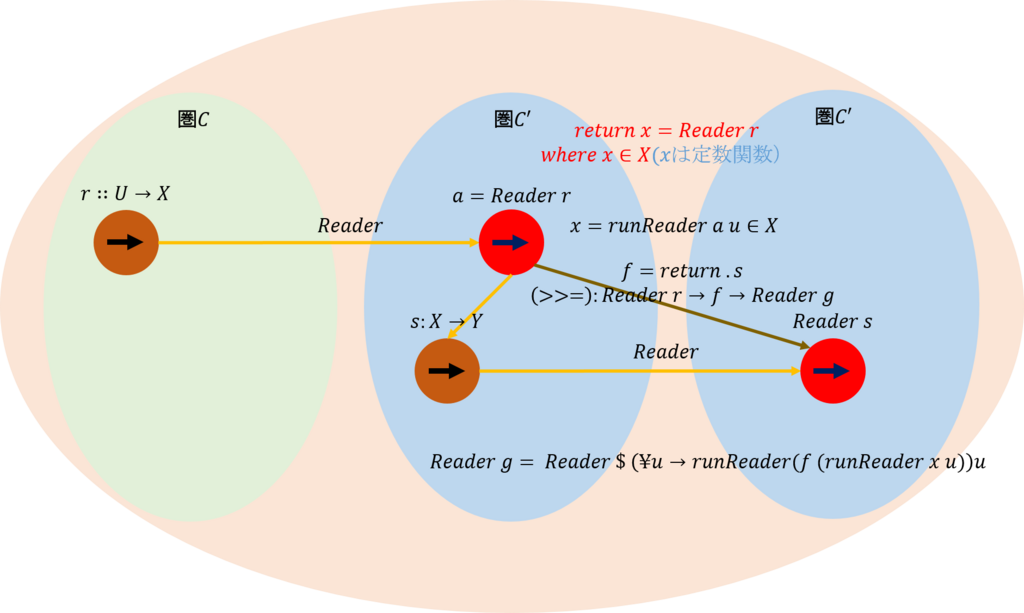
\( ( >>=)\)は基本的には、二つの関数の合成である。上の図であれば、\(Reader \ r\)と\(Reader \ s\)との合成である。\(Reader \ r\)を実行して、その出力を\(Reader \ s\)の入力として渡せばよい。入力となる値は、\(runReader (Reader \ r) \ u\)である。しかし、\(Reader \ s\)はこれを受け取れるようにはなっていないので、可能な形に変換する必要がある。それには、受け取った入力を\(s\)で変換し、それを戻す定数関数を作ればよい。これをしてくれるのは、先ほど示した\(return\)である。そこで、\(return . s\)とすればよい。従って、\(>>=\)への入力は、\(Reader \ r\)と\(f=return . s\)となる。
\(>>=\)からの出力は、\(Reader \ g\)である。そして、\(g\)は、入力を\(\backslash u\)とし、出力を\(runReader (f \ (runReader (Reader \ r) \ u)) \ u \)とする関数である。
従って、\(>>=\)は、\(Reader \ r\)を\(x\)で置き換えると次のように定めることができる。
x >>= f = Reader $ \u -> runReader (f (runReader x u)) u
少し、用いてみよう。\(r=(*2),s=show\)の場合には、次のようになる。
*Main> a = Reader (*2) >>= return . show *Main> runReader a 5 "10"
\(r=show,s=length\)の場合には、次のようになる。これは、入力した数字の桁数を求める関数である。
*Main> b = Reader show >>= return . length *Main> runReader b 2018 4
最近のHaskellでは、モナドの上位クラスにアプリカティブが用意されている。従って、\(Reader\)と定義するためには、これも必要となる。ここでは、説明を省いて、アプリカティブを含めて、\(Reader\)に関連する定義を示そう。
import Control.Monad import Control.Applicative data Reader u a = Reader (u -> a) instance Functor (Reader r) where fmap f (Reader r) = Reader $ f . r instance Applicative (Reader r) where pure x = Reader $ \u -> x (Reader f) <*> (Reader x) = Reader $ \u -> (f u) (x u) instance Monad (Reader r) where return x = Reader $ \u -> x x >>= f = Reader $ \u -> runReader (f (runReader x u)) u runReader :: Reader u a -> u -> a runReader (Reader f) u = f u ask :: Reader a a ask = Reader $ \u -> u