3.3 \(Reader\)と極限
ここまでの記事で、\(Reader\)の使い方と定義について詳しく説明した。この記事では、さらに理解を進めるために、圏論での極限とのかかわりについて説明しよう。圏論は、様々な数学の分野で共通に成り立っている性質について論じる学問ともみなすことができるが、極限はその一つと言える。いわゆる積と呼ばれる概念が成り立つとき、そこには極限が存在するというのが、普遍に成り立つ性質である。このような性質は普遍性(universal property)と呼ばれ、数学での重要な概念である。
1)\(Reader\)と極限
ここでは、関手\(Reader\)にも、積という概念が成り立ち、そのため、極限と呼ばれる普遍性が成り立つことを説明する。
これまで説明してきたように、関手\(Reader\)は、ある圏の対象としての射\(r: U \rightarrow X\)を、別の圏の対象である射\(Reader \ r\)へと写すものである。また、モナドとしての性質も有している。
少し前の記事で錐について論じた。そこでは、インデックス圏\(\mathcal{I}\)から圏\(\mathcal{C}\)への関手を利用して、錐を作成した。それに倣って、ここでも、圏\(\mathcal{I}\)に二つの対象\(I,J\)を用意することとしよう。また、別の圏\(\mathcal{C}\)は、先ほど説明した対象\(Reader \ r\)で構成されているとしよう。そして、インデックス圏の対象\(I,J\)を\(\mathcal{C}\)へ関手により写すことにしよう。
関手\(D\)によって、それぞれを\(Raeder \ r_I\)と\(Raeder \ r_J\)に写す。ここで、\(r_I:U \rightarrow X_I\), \(r_J:U \rightarrow X_J\)である。
また、関手\(\Delta_C\)によって、それぞれを同じ\(Raeder \ s\)に写す。ここで、\(s:U \rightarrow Y\)である。ただし、\(Y\)は、\(X_I\)と\(X_Y\)のデカルト積とする。即ち、 \(Y= (X_I, X_J)\)である。これより次を得る。
\begin{eqnarray}
&& Reader \ s \\
&=& Reader \ $ \ U \rightarrow Y \\
&=& Reader \ $ \ U \ \rightarrow (X_I, X_J) \\
&=& Reader \ $ \ U \rightarrow (X_I \times X_J) \\
&=& Reader \ $ \ (U \rightarrow X_I) \times (U \rightarrow X_J) \\
&=& (Reader \ $ \ U \rightarrow X_I) \times (Reader \ $ \ U \rightarrow X_J) \\
&=& Reader \ r_I \times Reader \ r_J
\end{eqnarray}
これより、\(Reader \ s\)から\(Reader \ r_I \),\(Reader \ r_J\)に対して射が存在することが分かる(それぞれ第一要素、第二要素を出力とするものである)。
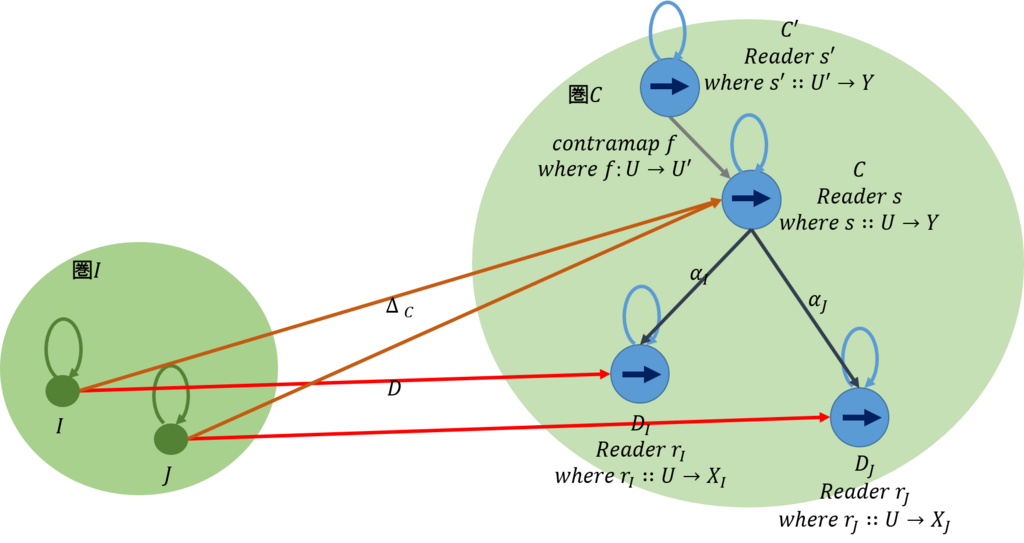
上記の関係を可換図式で示すと下図のようになる。

これより、\(Reader r_I\)と\(Reader r_J\)には積\(Reader r_I \times Reader r_J\)が存在することが分かる。従って、錐である。
このため、下図に示すように、任意の\(Reader \ s’\)について、一意的に定まる射が存在するような極限\( Reader \ s\)が存在する。なお、一意的に定まる射は、\(s:U \rightarrow Y\), \(s’:U’ \rightarrow Y\),\(f:U \rightarrow U’\)とした時、\(contramap f\)である。これを可換図式で示すと下図のようになる。
2)\(Reader\)の積とHaskellとの関係
それでは、いま説明した\(Reader\)の積はHaskellではどのような時に利用されるのだろうか。それを具体的な例でみてみよう。
いま「誰ですかと問われた」ときに、「トム」と答える関数と「ジェリー」と答える関数を用意したとしよう。
tom :: Reader String String tom = do env <- ask -- gives you the environment which in this case is a String return (env ++ " This is Tom.") jerry :: Reader String String jerry = do env <- ask return (env ++ " This is Jerry.")
それでは、二つの関数の積を考えることとしよう。これは、二つを実行し、その結果を一緒にして出力するような関数を用意したらどうであろうか。
tomAndJerry :: Reader String String tomAndJerry = do t <- tom j <- jerry return (t ++ "\n" ++ j)
さっそく実行してみよう。
*Main> runReader tomAndJerry "Who is this?" "Who is this? This is Tom.\nWho is this? This is Jerry."
積としての\(Reader\)を実感できたことと思う。
3)余極限との関係
\(Reader\)と極限の関係を示したので、その双対関係にあるものも存在するはずである。そこで、\(Reader\)の矢印の向きを変えた射\(Op\)を次のように定義する。
\begin{eqnarray}
Op \ $ \ r^{op} \\
r : U \rightarrow X
\end{eqnarray}
なお、上記の定義で、射\( r^{op}\)は、射\(r : U \rightarrow X \)の射の矢印の方向を反対にしたものである。
この定義に従うと、\(Op\)の可換図式は下図のようになる。
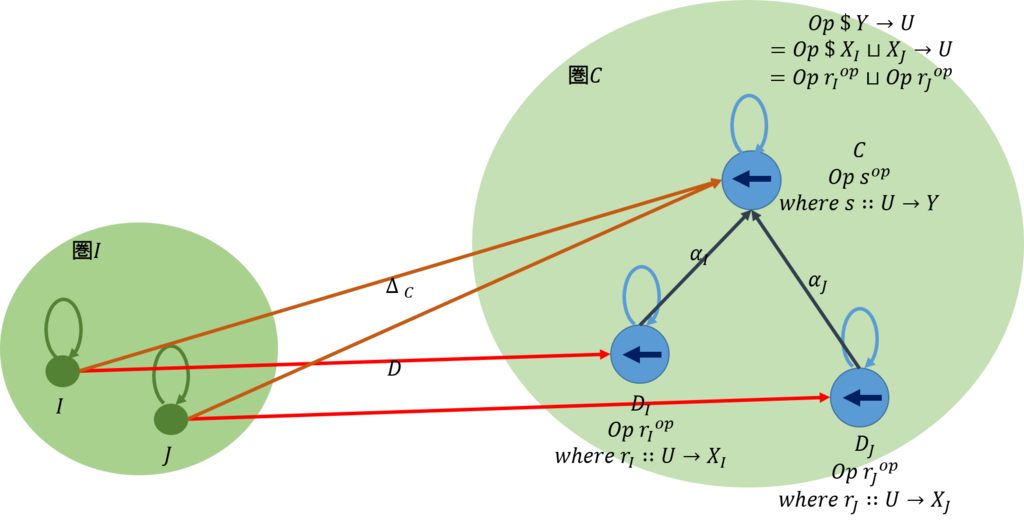
上図で圏\(\mathcal{I}\)はインデックス圏で、\(I,J\)はそこでのふたつの対象である。この対象は、関手\(D\)によって、ある圏\(\mathcal{C}\)の対象となっている射\(Op \ r_I^{op}, Op \ r_J^{op} \)に写される。また、関手\(\Delta_C\)によって、対象となっている一つの射\(Op \ s^{op} \)に写される。
そして、\(Op \ s^{op}\)は次のように変換できる(ここで、\(s: U \rightarrow Y\)である。また、\(\sqcup\)は直和である)。
\begin{eqnarray}
&& Op \ s^{op} \\
&=& Op \ $ \ Y \rightarrow U \\
&=& Op \ $ \ (X_I \sqcup X_J) \rightarrow U \\
&=& Op \ $ \ (X_I \rightarrow U) \sqcup (X_J \rightarrow U) \\
&=& Op \ r_I^{op} \sqcup Op \ r_J^{op}\\
\end{eqnarray}
上図から、対象\(D_I=Op \ r_I^{op}\)と対象\(D_J=Op \ r_J^{op}\)から対象\(C=Op \ s^{op}\)への射が存在することは明らかである。従って、\(Op\)は余錐である。
これにより、\(Op\)は余極限を有するので、次の可換図式を得る。
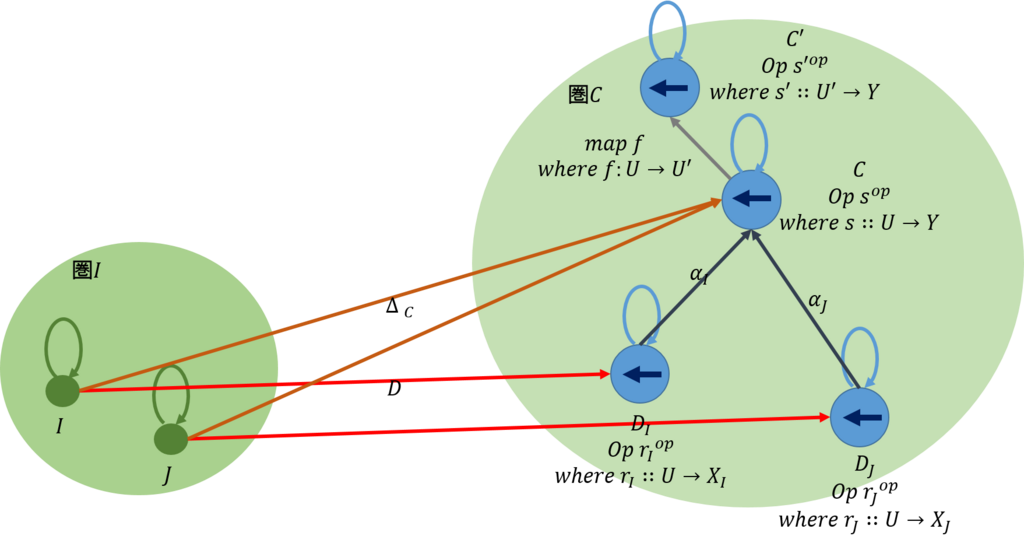
このように、\(Reader\)とその双対である\(Op\)は、圏論での積と余積であり、それぞれ極限と余極限を有することが分かる。
なお、Haskellでは、\(Op\)を\(MonadReader\)と呼ばれるモナドとして定義されている。そして、\(ask\)という関数が、環境変数の値を呼び出すために用意されている。