1.モナド
クリスマスパーティーは大きくなった孫たちが集まりとても賑やかだった。今年は、ターキーを2羽焼いた。例によって、ブライン液につけ、ジューシーな味を楽しんだ。
1.1 モナドの本来の意味
モナドって何ですかと問われたとき、何と答えるであろうか。数学やプログラミングに馴染みのある人は、この分野での専門用語の一つと答えることだろう。ウィキペディアで調べると、哲学でも使われていることが分かる。実はこちらの方が古くて、数学やプログラミングの分野で使われているモナドは、哲学の分野からの借用語だ。
モナドは、ギリシャ語のモナス(monas)に由来する。モナスは単子と訳されるが、それは単位としての1が原義だ。ピタゴラス(Pythagoreans)によって用いられ、ライプニッツ(Leibniz)によって発展させられた概念である。
モナドの概念を『ブリタニカ国際大百科事典』から引用すると「モナドは部分をもたない単純な実体で,物質的ではなく霊的である。生成消滅することはなく,そこに起る一切の変化は内的原理に由来し、表象によって全世界と全歴史を表現する。表象を変化させる通時的原理は欲求である。モナドは外からの影響を受けないから,モナド間に因果関係はなく、相互間の関係は予定調和の原理で説明される。世界は低級な物体から神にいたるモナドによって構成されており,この位階はそれぞれのモナドの含む表象の明瞭度による」となる。
今日の視点で見ると、ライプニッツの説明は宗教的で神秘的な雰囲気だが、モナドという概念を記述するためのキーワードは、単純な実体と表象のように見える。そして、表象は単純な実体を外に見せるための表現と捉えてよさそうだ。さらに、表象は時間的な変化により明瞭度での濃淡もあるようだ。図で示すと次のようになるだろうか。
歴史研究においては、歴史史料が重要な役割をなす。歴史史料は、事件の様子を伝えてくれる表象だと若尾さんは述べ、史料の扱い方について説明する。百姓一揆を研究するために使われる歴史史料には、百姓たちが幕府や藩に対して訴えた願書や、逆に百姓たちに命じる触書や、あるいは一揆の様子を叙述的に記述した物語などがある。願書や触書は事件の内容を直接伝えてくれるので一次史料と呼ばれ、物語などはエンターテインメント性をもたらせるために脚色されていて、当てにならないことが含まれているので、二次史料と言われる。モナドの説明に従えば、一次史料は明瞭度の高い表象であり、二次史料は明瞭度で劣る表象ということになる。そして、一揆という事件そのものは単純な実体だ。
話はモナドの説明とは少しずれるが、著者は、本の中で、一次史料だけ扱っていればよいのかと問いかける。歴史家たちが拠り所にしていた一次資料を精査すると、願書や触書には、前の事件を真似て書いたものが多いことに気がつくそうだ。現在の言葉で言うならばコピペが満ち溢れているということだろう。このため歴史研究をする上で、一次史料は必ずしも重宝に使っていればよいというものではないと言う。一次史料、二次史料を上手に利用して、そこから飾られた部分を除いて、真実の部分を探求することが重要だと教えてくれる。話は外れたが、事件を説明する歴史史料を表象という言葉で説明していることが、モナドの概念を深めてくれ、有意義な説明であった。
1.2 モナドの定義を試みる
話を元に戻そう。数学やプログラミングで用いるモナドは、哲学の分野で使われている概念を引き継いでいると言われている。高校数学の範囲の中で探すと、冪集合がそうだろう。ある集合の冪集合とは、その部分集合の全てを要素とする集合である。例えば集合\(A\)が3要素\( \{a,b,c\} \)からなるとする。それでは、この冪集合を求めてみよう。1)部分集合の中に複数の同じ要素が入っているものは一つにまとめられること、2)要素の出現順序は変えても構わないことに注意すると、求める冪集合は
\begin{eqnarray}
P(A)&=\{& \{\}, \{a\}, \{b\}, \{c\}, \\
&&\{a,a\}, \{a,b\}, \{a,c\}, \\
&&\{b,a\}, \{b,b\}, \{b,c\}, \\
&&\{c,a\}, \{c,b\}, \{c,c\}, \\
&&\{a,b,c\}\} \\
&=\{& \{\}, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, \{a,b,c\}\}
\end{eqnarray}
となる。今得られた冪集合に対して、さらに冪集合を作ることができる。これを下図に示そう。なお煩雑になることを避けるため2要素\( \{1,2\} \)にした。

\(return\)は最も明瞭度の高い表象を作り出し、\(join\)は操作を繰り返しているうちに最も明瞭度の高い表象に至ることに気がつく。\(return\)も\(join\)も最も明瞭度の高い表象に向かうということに特徴がありそうだ。モナドを構成するときに、この性質を取り入れることが重要に思える。それ以上に重要なことは、カプセル化をしている\(T\)だろう。
そこでこれらを用いて、圏を試しに構成してみよう。圏の名前は、\(\mathcal{C}\)としよう。そして、対象は、単純な実体と表象たちだ。即ち、\( A,T(A),T(T(A)),…\)だ。射は、先ほど定義した\( return\)と\( join \)だ。また、恒等射は、\( I_{A},I_{T(A)},I_{T(T(A))},… \)だ。射の合成は\(\circ\)とし、また単位律、結合律は成り立っているとする。そして、\(T\)は、\(\mathcal{C}\)から\(\mathcal{C}\)への関手としよう。即ち、自己関手だ。まとめると試案の圏は以下のようになる。
圏\(\mathcal{C}\)の構成 (試案)
対象:\( A,T(A),T(T(A)),…\)
射:\( return : A \rightarrow T(A), join : T(T(A)) \rightarrow T(A) \)
恒等射:\( I_{A},I_{T(A)},I_{T(T(A))},… \)
合成:\(\circ\)
単位律:省略
結合律:省略
図で示すと下図のようになる。
圏\(\mathcal{C}\)の構成
対象:\( \mathcal{A},T(\mathcal{A}),T(T(\mathcal{A})),…\)
射:\( return : \mathcal{A} \rightarrow T(\mathcal{A}), join : T(T(\mathcal{A})) \rightarrow T(\mathcal{A}) \)
恒等射:\( I_{\mathcal{A}},I_{T(\mathcal{A})},I_{T(T(\mathcal{A}))},… \)
合成:\(\circ\)
単位律:省略
結合律:省略
これで、圏\(\mathcal{C}\)が出来上がった。細部も加えて示したのが下図である。
1.3 Haskellのモナドで確認する
モナドを表すための候補が出てきたので、先に進める前に、本当にそうなのかを、Haskellでのモナドの定義を利用して確認してみよう。Control.Monadのパッケージを見ると次のようになっている。
class Applicative m => Monad m where (>>=) :: forall a b. m a -> (a -> m b) -> m b (>>) :: forall a b. m a -> m b -> m b m >> k = m >>= \_ - > k return :: a -> m a return = pure fail :: String -> m a fail s = errorWithoutStackTrace s
さらに、これらのメソッドは単位律と結合律を満たすものとする。
Haskellでのモナドのクラスで用意しなければならないメソッドは、\(return\)とバインド(bind)と呼ばれる\((>>=)\)だ。しかし\(return\)はモナドの上位クラスであるアプリカティブ(Applicative)で定義されるので、モナドのところで定義する必要があるメソッドは\((>>=)\)だけだ。2番目のメソッド\((>>)\)は、バインドを用いて定義されているので、定義する必要はないし、またそれほど重要なメソッドでもない。
繰り返しになるが、Haskellのモナドで重要なメソッドは\( (>>=)\)と\(return\)である。そこで、冪集合がモナドであるという推察を確認するためには、冪集合のところで得た\( return\)と\(join\)が、Haskellでのメソッド\(return\)と\((>>=)\)に対応していることを示さなければならない。
| 式 | 冪集合 | Haskell |
|---|---|---|
| 1 | \( return : A \rightarrow P(A) \) | \(return :: a \rightarrow m \ a\) |
| 2 | \( join : P(P(A) \rightarrow P(A) \) | \((>>=) :: forall \ a \ b. \ m \ a \rightarrow (a \rightarrow m \ b) \rightarrow m \ b\) |
上の表で、式1は対応していることが分かる。しかし、式2、即ち\(join\)と\( (>>=)\)は対応しているとは即断しがたい。そこで、Haskellでの定義を変形してみよう。モナド\(m\)は関手なので、
\begin{eqnarray}
m \ a \rightarrow (a \rightarrow m \ b)
\end{eqnarray}
の部分は、下図のように表すことができる。
\begin{eqnarray}
m \ a \rightarrow (a \rightarrow m \ b) & = & (fmap \ f \ (m \ a)) \\
& = & m (f (a)) \\
& = & m (m \ b)
\end{eqnarray}
となる。まとめると、
\begin{eqnarray}
m \ a \rightarrow (a \rightarrow m \ b) \rightarrow m \ b \\
= m (m \ b) \rightarrow m \ b
\end{eqnarray}
である。\(b\)を\(a\)で置き換えると、
\begin{eqnarray}
m (m \ a) \rightarrow m \ a
\end{eqnarray}
となり、\(join\)同じであることが分かる。
これで、冪集合から得られた2関数がモナドを定義するのに必要な関数であるという裏付けを得たので、さらに議論を進めることにしよう。
1.4 汎用化する
一般的なモナドの定義に近づけるために、\( return,join\)を\(η,μ\)で置き換え、汎用化してみよう。
\begin{eqnarray}
η &:& A & \rightarrow & T(A) \\
μ &:& T(T(A) & \rightarrow & T(A)
\end{eqnarray}
さらに、\(T(A),T(T(A)),…\)は同じ薄茶色で表し、薄緑色の部分をなくすと、前に示した図は次のように表すことができる。
\begin{eqnarray}
η &:& I(A) & \rightarrow & T(A) \\
μ &:& T(T(A) & \rightarrow & T(A)
\end{eqnarray}
上記の式は任意の\(A\)について成り立つので、\(A\)を省くと
\begin{eqnarray}
η &:& I & \rightarrow & T \\
μ &:& T \circ T & \rightarrow & T
\end{eqnarray}
と記述することができる。そこで、圏\(\mathcal{C}\)を対象とし、関手\(T\)を射とし、モナドを表す圏\(\mathcal{D}\)をつぎのように定義できる。
圏\(\mathcal{D}\)の構成
対象:圏\(\mathcal{C}\)
射:\(T: \mathcal{C} \rightarrow \mathcal{C} \)
恒等射:\(I_\mathcal{C} \)
合成:\(\circ\)
そして、次のように、単位律、結合律を満たすものとする。
単位律:\(I_\mathcal{C} \circ T= I_\mathcal{C} = T \circ I_\mathcal{C} \)
結合律:\( (T \circ T) \circ T = T \circ (T \circ T) \)
圏\(\mathcal{D}\)は、さらに
\begin{eqnarray}
η&:& I_\mathcal{C} & \rightarrow & T \\
μ&:& T \circ T & \rightarrow & T
\end{eqnarray}
を満たすものとする。ここでは、\(η: I \rightarrow T \)から\(η: I_\mathcal{C} \rightarrow T \)に変えている。恒等射の定義域が単純な実体の領域から表層の領域まで含むようになったが、\(η: I_T \rightarrow T \circ T \rightarrow T \)であることから、矛盾なく拡張することが可能である。
圏\(\mathcal{D}\)を図で示すと以下のようになる。
この圏をしばらく観察してみよう。対象\(\mathcal{C}\)を小さくし、射\(T\)、恒等射\(I_\mathcal{C}\)、そしてこれらから合成される射を描くと下図のようになる。
1.5 精錬化する
これまでの議論でモナドの定義は出来上がったが、もう少し綺麗に纏めることにしよう。\(η, μ\)が関手から関手への射になっているので、自然変換と見なせる。
自然変換を復習しておこう。圏\(\mathcal{C}, \mathcal{D}\)があり、前者から後者へ関手\(F,G\)が存在したとする。このとき、\(F\)から\(G\)への射\(η\)が自然変換であるとは、\(\mathcal{C}\)の任意の対象\(A,B\)とその間のやはり任意の射\(f\)に対して、\(\mathcal{D}\)で\( G(f) \circ η_A = η_B \circ F(f)) \)が成り立つことである。この関係を下図に示す。
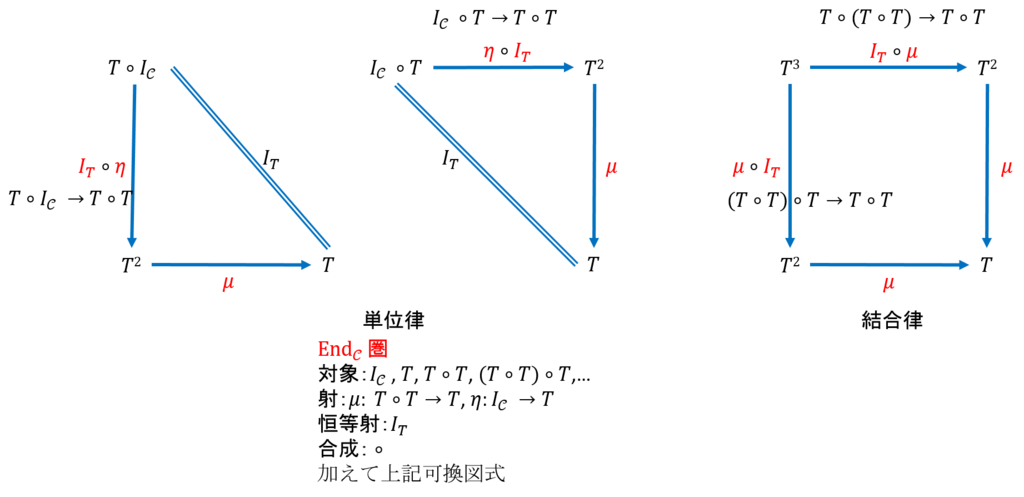
圏\( \mathbf{End}_\mathcal{C} \)の構成
対象:\(I_\mathcal{C}, T, T \circ T \)
射:\( η: I_\mathcal{C} \rightarrow T, μ: T \circ T \rightarrow T \)
恒等射:\(I_ T : T \rightarrow T\) (注意:これは恒等変換である)
合成:\( \circ \)
単位律:\( μ \circ (I_T \circ η) = I_T = μ \circ (η \circ I_T) \)
結合律:\( μ \circ (I_T \circ μ) = μ \circ (μ \circ I_T) \)
となる。図で表すと以下のようになる。
モナドの定義が出来上がったので、圏論での最も重要な概念である随伴との関係について述べておこう。ウィキペディアでは随伴は次のように定義されている。圏\(\mathcal{C}\)と\(\mathcal{D}\)との間の随伴とは、二つの関手
\begin{eqnarray}
L: \mathcal{D} \rightarrow \mathcal{C} \\
R: \mathcal{C} \rightarrow \mathcal{D}
\end{eqnarray}
の対であって、全単射の族
\begin{eqnarray}
{\rm Hom}_{\mathcal{C}}(L(Y),X) \cong {\rm Hom}_{\mathcal{D}}(Y,R(X))
\end{eqnarray}
が変数\(X,Y\)に対して自然となるものをいう。このとき、関手\(L\)を左随伴関手と呼び、\(R\)を右随伴関手と呼ぶとなっている。図で表すと、
しかし、上記の定義からモナドとの関係を説明するのは煩雑になるので、もう一つの定義を使うことにしよう。それは、やはりウィキペディアで次のように定義されている。
圏\(\mathcal{C}\)と\(\mathcal{D}\)の余単位・単位随伴は二つの関手
\begin{eqnarray}
L: \mathcal{D} \rightarrow \mathcal{C} \\
R: \mathcal{C} \rightarrow \mathcal{D}
\end{eqnarray}
および二つの自然変換
\begin{eqnarray}
η: I_\mathcal{D} \rightarrow R \circ L \\
ε: L \circ R \rightarrow I_\mathcal{C}
\end{eqnarray}
であって(ηは単位、εは余単位と呼ばれる)、これらの合成
\begin{eqnarray}
L =L \circ I_\mathcal{D} \xrightarrow{L \circ η} L \circ R \circ L \xrightarrow{ε\circ L} L \\
R = I_\mathcal{D} \circ R \xrightarrow{η\circ R} R \circ L \circ R \xrightarrow{R \circ ε} R
\end{eqnarray}
がそれぞれ\(L\)と\(R\)上の恒等変換\(I_L,I_R\)となることをいうとなっている。これは三角恒等式(triangle identities)と呼ばれる。これを可換図式で示そう。
\begin{eqnarray}
T=R \circ L
\end{eqnarray}
としてみよう。モナド側の\(η\)を得ることは次に示すように簡単である。
\begin{eqnarray}
I_\mathcal{D} \xrightarrow{η} R \circ L = T
\end{eqnarray}
それでは\(μ\)について考えよう。次のように変換して求めることができる。
\begin{eqnarray}
T \circ T = R \circ L \circ R \circ L \xrightarrow{R \circ ε \circ L} R \circ I_\mathcal{C} \circ L = R \circ L = T
\end{eqnarray}
図示すると次のようになる。
1.6 モナドと随伴の関係
圏\( \mathbf{End}_\mathcal{C} \)の単位律、結合律を随伴から得てみよう。まず単位律から始める。
\begin{eqnarray}
L \xrightarrow{L \circ η} L \circ R \circ L \xrightarrow{ε\circ L} L \\
R \xrightarrow{η\circ R} R \circ L \circ R \xrightarrow{R \circ ε} R
\end{eqnarray}
と、およびそれぞれで左辺と右辺は恒等変換になっていることを利用すると
\begin{eqnarray}
T \circ I_\mathcal{D} = R \circ L \circ I_\mathcal{D} \xrightarrow{R \circ L \circ η} R \circ L \circ R \circ L \xrightarrow{R \circ ε \circ L} R \circ L = T \\
I_\mathcal{D} \circ T = I_\mathcal{D} \circ R \circ L \xrightarrow{η \circ R \circ L} R \circ L \circ R \circ L \xrightarrow{R \circ ε \circ L} R \circ L = T
\end{eqnarray}
を得る。またそれぞれで左辺と右辺は恒等変換になっていることもわかる。可換図式で示すと下図のようになる。
次は結合律だ。単位律と同様に式を展開することで得ることができる。その過程を可換図式で示しておこう。
1.7 冪集合をHaskellで実装する
無事にモナドを定義することができたので、考える出発点であった冪集合に戻り、これをHaskellで実現することとしよう。
ここでは、集合をリストで表すこととしよう。例えば、要素\(a,b,c\)からなる集合は\([a,b,c]\)と表すことにする。冪集合は、それぞれの要素に対して、含むか含まないかの組合せを作ることだ。リストは\((x:xs)\)と表すことができるので、\(xs\)で作られる冪集合の部分集合のそれぞれに要素\(x\)をつけたものとつけないものとの和集合となる。
\(xs\)から作られた冪集合を\(rest\)とし、これに要素\(x\)をつける操作は
rest >>= (return . (x:))
である。
確認しておこう。
Prelude> import Control.Monad *Main Control.Monad> [[2,3],[2],[3]] >>= (return . (1:)) [[1,2,3],[1,2],[1,3]]
従って、要素\(x\)をつけるかつけないかを、ブール値\(b\)で判断するプログラムは次のようになる。
\b -> if b then rest >>= (return . (x:)) else rest
これを用いてみよう。
*Main Control.Monad> f x rest = \b -> if b then rest >>= return . (x:) else rest *Main Control.Monad> [True, False] >>= f 1 [[2,3],[2],[3]] [[1,2,3],[1,2],[1,3],[2,3],[2],[3]]
少し、工夫をして、\(x\)の値を外から与えられるようにしよう。
\x -> const [True, False] x >>= \b -> if b then rest >>= (return . (x:)) else rest
確認しよう。
*Main Control.Monad> g rest = \x -> const [True, False] x >>= \b -> if b then rest >>= (return . (x:)) else rest *Main Control.Monad> g [[2,3],[2],[3]] 1 [[1,2,3],[1,2],[1,3],[2,3],[2],[3]]
次に\(rest\)の部分を再帰的に構成できるようにしよう。次のようになる。そして関数名を\(power set\)としよう。
powerset [] = return [] powerset (x:xs) = const [True, False] x >>= (\b -> if b then powerset xs >>= (return . (x:)) else powerset xs)
確認しよう。
*Main Control.Monad> powerset [1,2,3] [[1,2,3],[1,2],[1,3],[1],[2,3],[2],[3],[]]
今求めた関数\(power set\)の構造を圏論のモナドを用いて描くと下図のようになる。
Haskellでは、より汎用的な\(filterM\)が用意されているので、\(Power set\)はこれを用いて次のように定義すればよい。
powerset = filterM (const [True, False])
一応確認しておこう。
Prelude> import Control.Monad *Main Control.Monad> powerset = filterM (const [True, False]) *Main Control.Monad> powerset [1,2,3] [[1,2,3],[1,2],[1,3],[1],[2,3],[2],[3],[]]
出来上がりだ。モナドを定義するために、冪集合から初めて、最後はまた冪集合に戻ってきた。クリスマスプレゼントとはいえ、長い記事になってしまったが、モナドを様々な面から観察することができ、新たな発見もあって、楽しむことができた。読者の方はいかがでしたか。