極限－錐

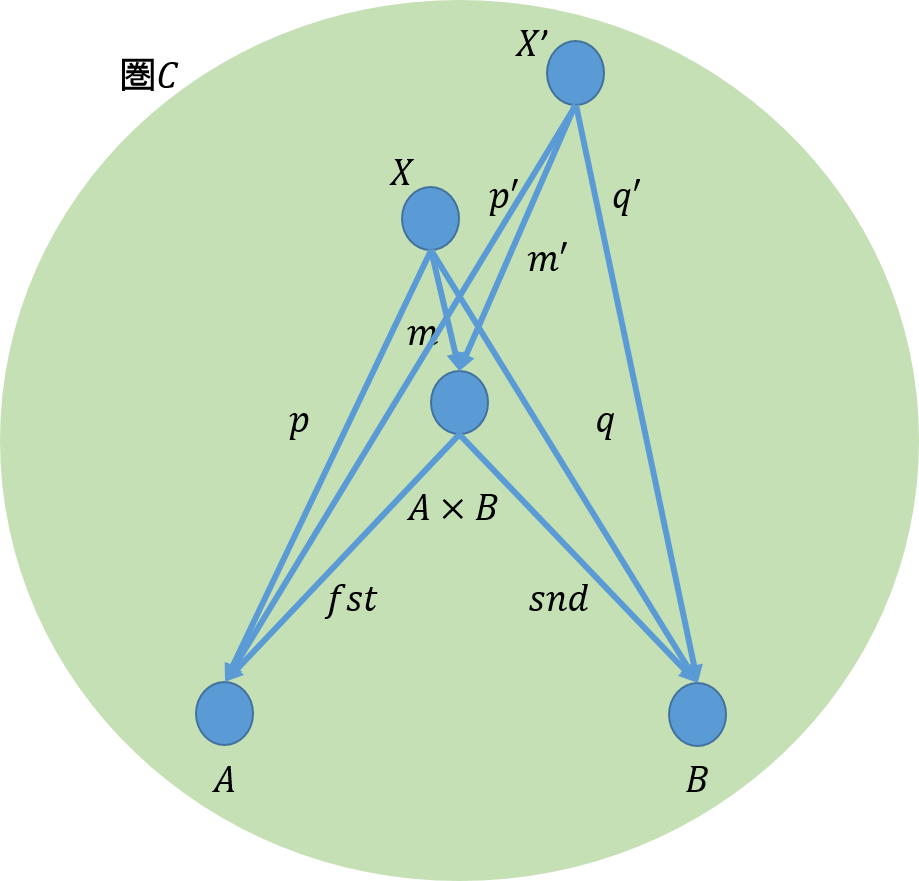
１．４　錐

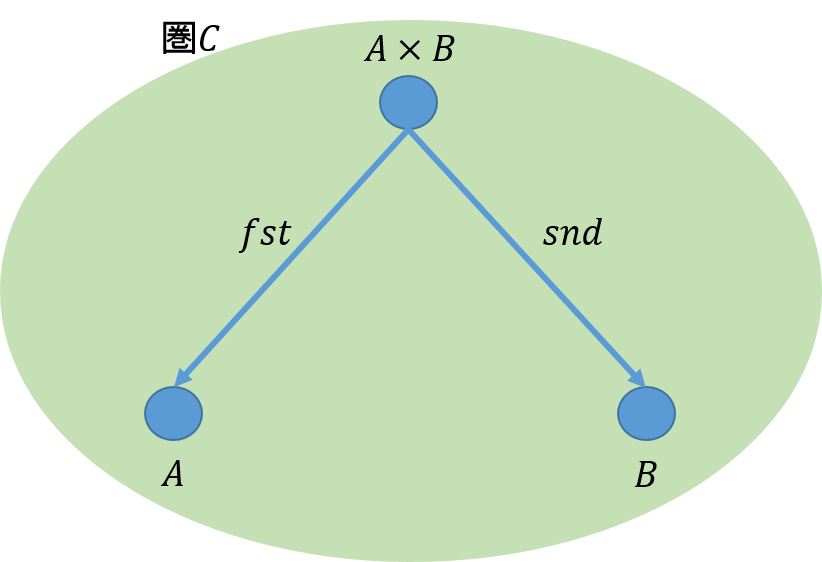
これまで、2回にわたって、圏論での極限の具体的な例を示してきた。そこでは、二つの対象\(A\),\(B\)とその極限\(A \times B\)ということで説明をした。また、極限は、ある条件を満たすものの中で最も良いものといういい方もした。また、ある条件を満たすものを候補とも説明した。

それでは、このような候補はどのようにして選ばれるのであろうか。あるいはさらに戻って、二つの対象はどのようにして選ばれるのであろうか。これらを選ぶ基準がないと、極限という概念を組み立てていくことができない。

そこで、ここでは、これらの選び方について説明することとする。

2対象からの錐

まず単純な例から説明しよう。二つの圏が与えられているとする。

一つの圏は、二つの対象\(1\),\(2\)しか有しない離散的な圏としよう(下図)。即ち、射は恒等射\(id\)しか有しないものとしよう。これを圏\(\bf{2}\)と呼ぶことにしよう。

もう一つの圏を\(\mathcal {C}\)と呼ぶことにし、ここから二つの対象を適当に選び、これを\(A\),\(B\)にしたとしよう。そこで、圏\(\bf{2}\)からこれらの対象に関手\(D\)を張ることを考えよう。これは、
\begin{eqnarray}
A=D(1) \\
B=D(2) \\
id_A=D(id_1) \\
id_B=D(id_2)
\end{eqnarray}
となるような\(D\)が存在するならば、関手を張ることが可能である。ここで、\(id_1,id_2,id_A,id_B\)はそれぞれの対象での恒等射である。

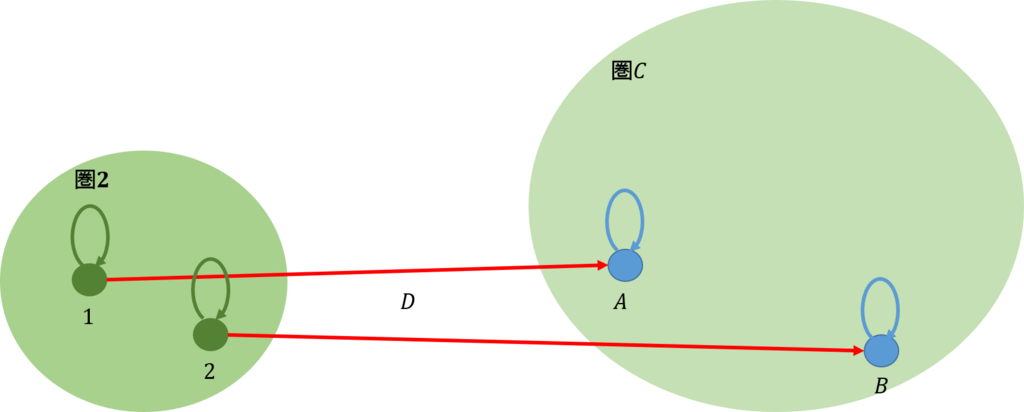
このような関手が張れたとしよう(上図)。そして、\(\mathcal {C}\)からもう一つ対象を選んできたとし、これを\(C\)としよう。これに対して、圏\(\bf{2}\)からこの対象に関手\(\Delta_C\)を張ることを考えよう。同じように
\begin{eqnarray}
C=\Delta_C (1) \\
C=\Delta_C (2) \\
id_{C}=\Delta_C (id_1) \\
id_{C}=\Delta_C (id_2)
\end{eqnarray}
となるような\(C\)が存在するならば、関手を張ることが可能である。ここでも満たしたとしよう(下図)。

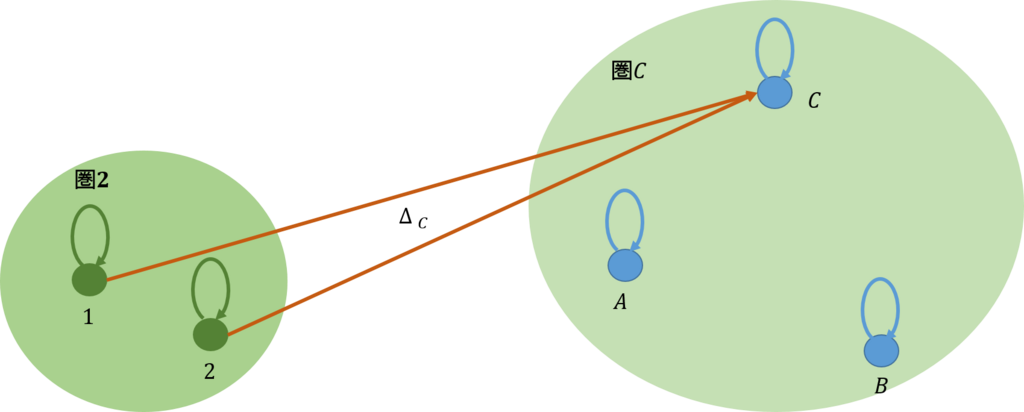
そこで、\(D\)から\(id_{C}\)への自然変換を考えよう。

自然変換

それでは、自然変換を復習しておこう。

下図に示すように、圏\(\mathcal{C}\)から圏\(\mathcal{C'}\)に対して関手\(D,D'\)が存在したとしよう。

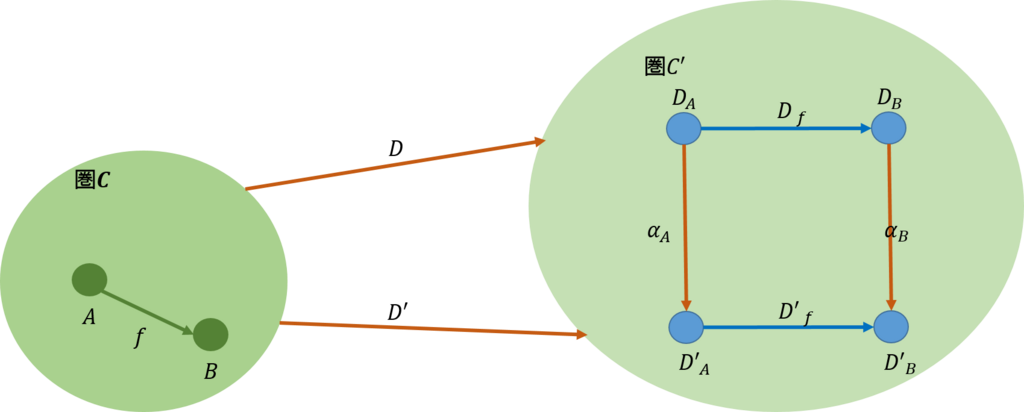
関手\(D\)から\(D'\)への自然変換\(Nat(D,D')\)とは、\(\mathcal{C}\)の任意の対象\(A,B\)に対して、上図が可換になることを言う。なお、\(A\)から\(B\)への射を\(f:A \rightarrow B\)とする。

上図は次のようになっている。
\begin{eqnarray}
D_A = D (A) \\
D_B = D (B) \\
D_f = D (f) \\
D'_A = D' (A) \\
D'_B = D' (B) \\
D'_f = D' (f)
\end{eqnarray}
である。

従って、可換は、\(\alpha_B \circ D_f ＝ D'_f \circ \alpha_A\)を満たすこととなる。

圏\(\bf{2}\)からの自然変換

それでは、圏\(\bf{2}\)の自然変換を考えてみよう。(下図)。

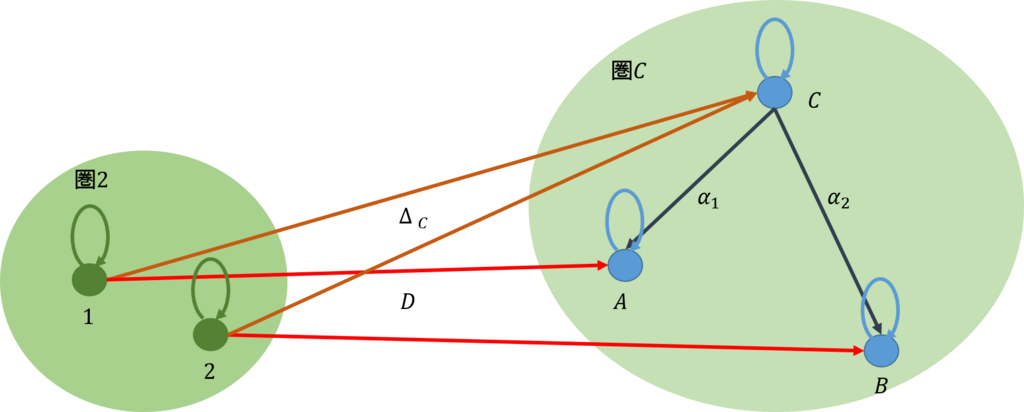
例えば、圏\(\bf{2}\)での対象1について考えよう。これは、\(D\)によって\(A\)に、\(\Delta_C\)によって\(C\)に写像変換されている。\(C\)から\(A\)への写像を\(\alpha_1\)とすると、これが自然変換を構成する要素となる。

対象2についても同様で、\(C\)から\(B\)への写像を\(\alpha_2\)とすると、これが自然変換を構成する要素となる。

なお、\(A\)と\(B\)の間には写像が存在しないので、可換の条件は存在しない。このため、\((\alpha_1,\alpha_2)\)は自然変換\(Nat(\Delta_C,D)\)となる。
一般には、自然変換は一つの組合せとは限らず、複数存在する。従って、可換を満たすものが\(n\)組ある場合には、\(Nat(\Delta_C,D)=\{(\alpha_1^1,\alpha_2^1),\{(\alpha_1^2,\alpha_2^2),...,\{(\alpha_1^i,\alpha_2^i)\}\)となる。

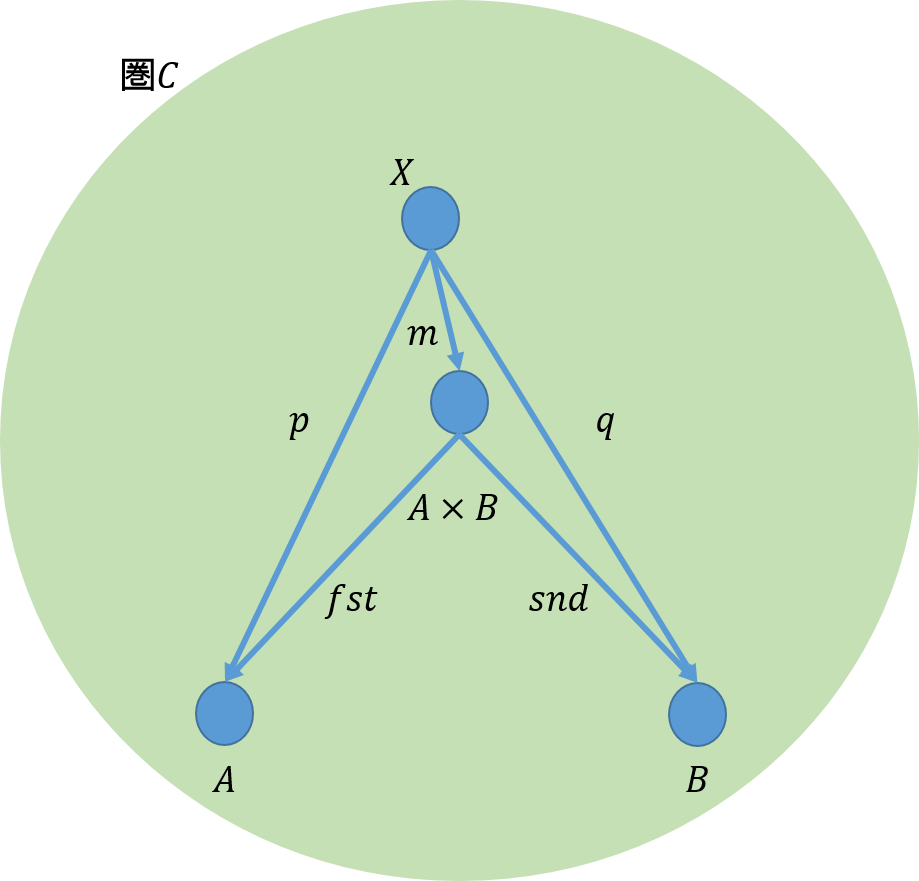
このようなものを選ぶことができるなら、\(C\)は\(A\)と\(B\)の積の極限への候補となる。

問題1：圏\(\bf{2}\)を利用して、二つの整数の公約数を選び出しなさい。
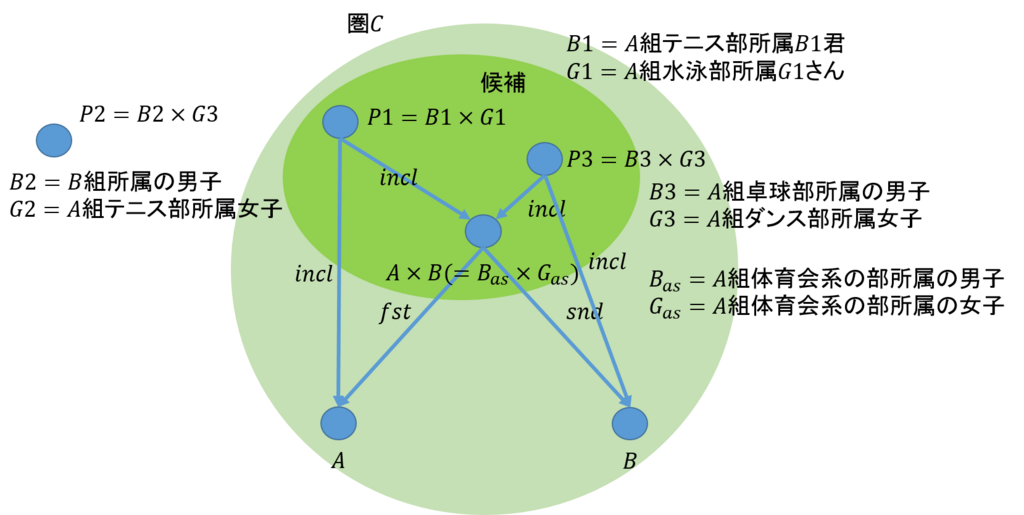
問題2：圏\(\bf{2}\)を利用して、料理作り好きな友人のリストの候補を作成しなさい。ヒント：知り合いを\(A\)とし、趣味を\(B\)を出発点に考えなさい。ここから絞っていくと、答えの一つとして、\(A\)は料理好きな友達の集まり、\(B\)は仏料理や和食のような種類の集まりを得る。

インデックス圏からの自然変換

圏\(\bf{2}\)をもう少し一般化してインデックス圏を用いてみよう。インデックス圏は、対象にインデックスが付加されており、対象間では射が定義されているものとする。ここでは、インデックス圏の中で最も単純な3つの対象からなるものを利用しよう。下図に示すように、インデックス圏\(\mathcal{I}\)と圏\(\mathcal{C}\)が存在したとしよう。

圏\(\bf{2}\)の場合と同じように、\(\mathcal{C}\)から三つの対象\(D_I,D_J,D_K\)を選んだとしよう。これらには\(\mathcal{C}\)から関手\(D\)で張ることができたとしよう(下図)。

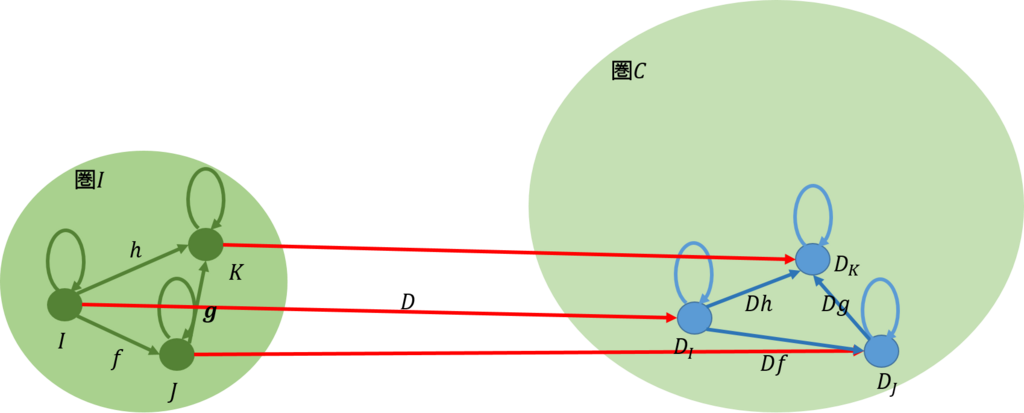
即ち、前回と同じように次が満たされたとする。
\begin{eqnarray}
D_I=D(I) \\
D_J =D(J) \\
D_K=D(K) \\
Df=D(f) \\
Dg=D(g) \\
Dh=D(h) \\
id_{D_I}=D(id_I) \\
id_{D_J}=D(id_J) \\
id_{D_K}=D(id_K)
\end{eqnarray}

次に、\(\mathcal{C}\)から一つの対象\(C\)を選んだとしよう。これらには\(\mathcal{C}\)から関手\(\Delta_C\)で張ることができたとしよう(下図)。

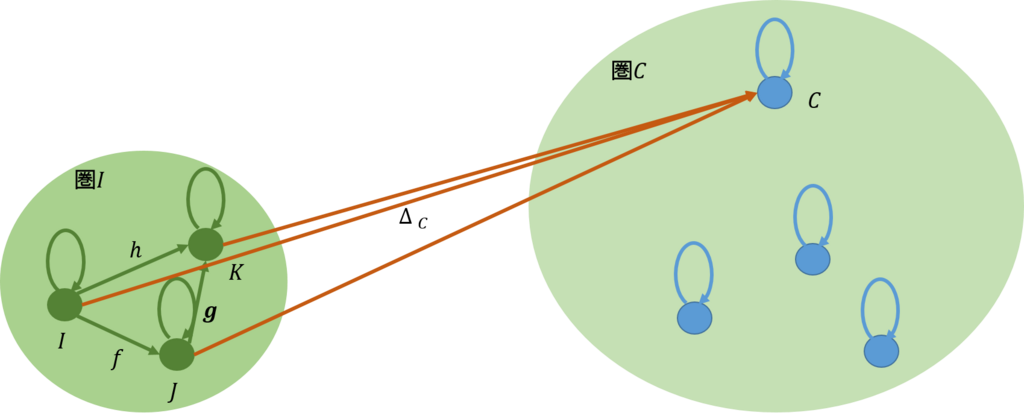
即ち、次が満たされたとする。
\begin{eqnarray}
C=D(I) \\
C =D(J) \\
C =D(K) \\
id_{C }=\Delta_C f =\Delta_C(f) \\
id_{C }=\Delta_C g =\Delta_C(g) \\
id_{C }=\Delta_C h=\Delta_C(h) \\
id_{C }=D(id_I) \\
id_{C }=D(id_J) \\
id_{C }=D(id_K)
\end{eqnarray}

ここで、関手\(\Delta_C\)から関手\(D\)に対して自然変換が成り立ったとしよう(下図)。

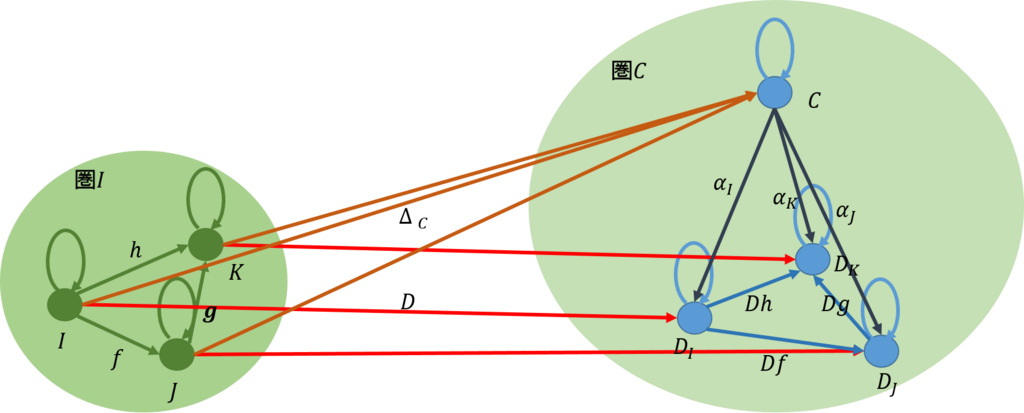
自然変換は、ドメインとなった圏の対象ごと、ここではさらに射もあるので射ごとにも、ドメイン側の圏で、移されたものの間を射で結んだ時に、可換を保持しなければならない。これは、圏\(\bf{2}\)の時の説明と同じである。

このため、対象\(I,J,K\)に対して、射\(\alpha_I:C \rightarrow D_I, \alpha_I:C \rightarrow D_J,\alpha_I:C \rightarrow D_K\)が存在し、可換の条件を満たさなければならない。

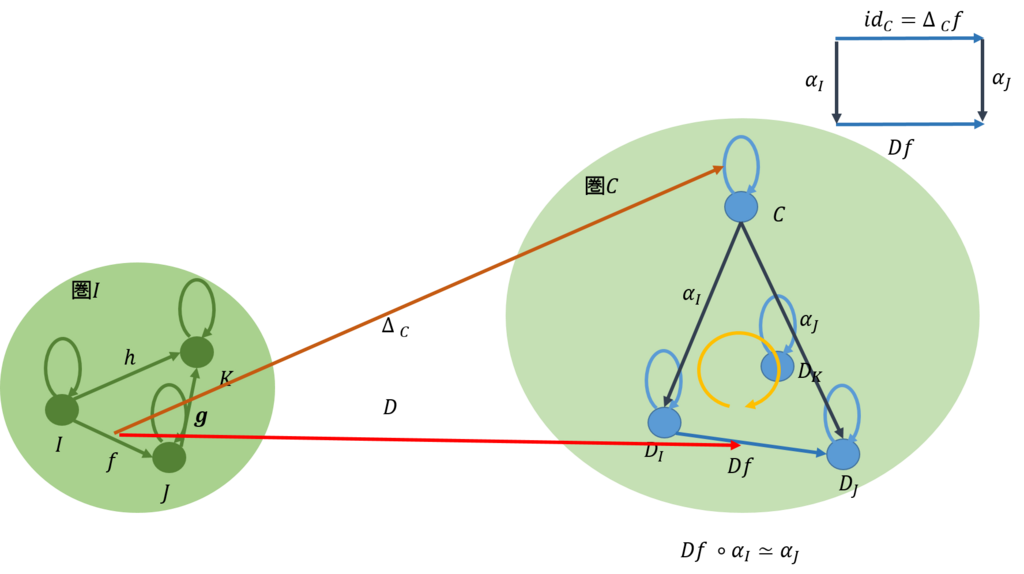
まず、射\(f\)に対しては、次のことが満たされなければならない(上図)。

即ち、
\begin{eqnarray}
\alpha_J = Df \circ \alpha_I
\end{eqnarray}

同様に射\(g\)に対して、
\begin{eqnarray}
\alpha_K = Dg \circ \alpha_J
\end{eqnarray}
が成り立ち、射\(h\)に対して、
\begin{eqnarray}
\alpha_K = Dh \circ \alpha_I
\end{eqnarray}
が成り立たなければならない。

この結果、下図に示すように、\(C\)を頂点として形作られた三角錐(\(C,D_I,D_J,D_K\))は、そのすべての側面において可換であるならば、自然変換である。即ち、\(\{(\alpha_I,\alpha_J,\alpha_K)\}\)は自然変換\(Nat(\Delta_C,D)\)の一つである。一般にはこのようなものは一つとは限らない。\(i\)個存在するとするならば、自然変換は\(Nat(\Delta_C,D)=\{(\alpha_I^1,\alpha_J^1,\alpha_K^1),(\alpha_I^2,\alpha_J^2,\alpha_K^2),...,(\alpha_I^i,\alpha_J^i,\alpha_K^i)\}\)である。

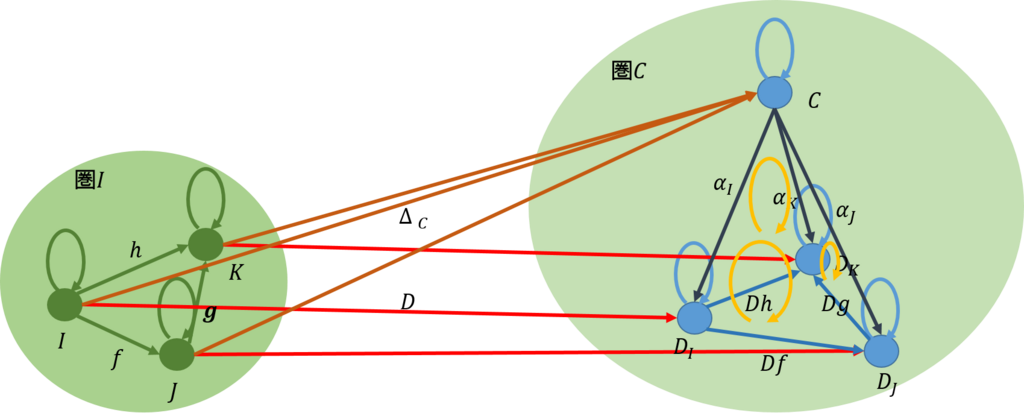
今回は、3つの対象からなるインデックス圏を用いて三角錐を得た。インデックス圏の対象を増やしていくと三角錐は円錐へと近づいていく。圏論では、インデックス圏から得られるこのような物体を錐(cone)と呼んでいる。

極限の定義はこの錐を用いて定義できるが、その話は次回行う。

極限－例：最大公約数

１．３　最大公約数

前回の記事では、集合を利用して、圏論での積を説明した。また、積の普遍性についても説明した。これらをさらに進めると、極限になる。しかし、もう少し例を挙げて、極限の説明をするための準備をすることにしよう。

ここでは、集合から離れることにする。極限という言葉は使わないが、類似した概念は中学校の数学でも現れる。そう、最大公約数(GCD: greatest common divider)だ。二つの整数が与えられた時に、共通の約数で最大のものが最大公約数だ。

今、二つの整数360と420を選んだとしよう。このとき、二つの整数の共通の素数は、(2,2,3,5)である。従って、これらの中からいくつかを取り出して掛け合わせたものは公約数となる。例えば、(2,2,3)からの12、あるいは、(2,3,5)からの30などはこの二つの数の共通の約数である。また、全てを取り出した(2,2,3,5)からの60は最大公約数である。これらを\(X,X’,A \times B\)とし、360と420を\(A\),\(B\)で表すと、以下のような可換図式を得る。

この図は、前回の記事で積の極限を説明したときの図と同じものである。この図より、\(A \times B\)が、\(A \)と\(B \)の積の極限、すなわち最大公約数、になっていて、\(X\)や\(X’ \)などが、\(A \)と\(B \)の積の候補、すなわち公約数、であることが分かる。従って、候補の中でもっともよいものが極限、すなわち、公約数の中で最も優れたもの、この場合には大きいものが最大公約数となっている。

即ち、上記の図において、\(A\)と\(B\)に対する任意の公約数\(X\)は、最大公約数\(A \times B\)に対して、一意的な射\(m\)が存在し、
\begin{eqnarray}
fst \circ m = p \\
snd \circ m =q
\end{eqnarray}
である。ここで、\(fst:A \times B \rightarrow A \),\(snd:A \times B\)である。これにより、最大公約数は圏での積である。

上記の図は、公約数で表したが、これを、それぞれを構成する素数で表すと次のようになる。

この図で、公約数を、すなわち最大公約数の候補を、それを構成している素数の集合と見なすと、候補は、極限即ち最大公約数の部分集合となっていることが分かる。

これは、前回、集合と説明したときと同じで、その時も候補は極限の部分集合になっていた。このようにみていくと、最大公約数の場合も、前の例題と同じだということが分かる。

このため、個別に定義するのではなく、共通な概念として極限を考えたほうがよいということが分かる。

問題：最大公約数が作る圏をHaskellで作成しなさい。

コテージパイ - ひき肉料理をポテトでトッピングしたイギリス家庭料理

今日、紹介する料理は、イギリスの伝統的な家庭料理、コテージパイ(Cottage Pie)だ。ウィキペディアによれば、この名前が使われるようになったのは1791年で、このころ、ジャガイモが貧困層でも利用できるようになった。

ジャガイモは、ペルー南部のチチカカ湖畔が発祥とされている。ヨーロッパに伝わったのは1570年ごろで、スペイン人が持ち込んだ。その普及は緩やかだったようで、本格的にヨーロッパで栽培されるようになるのは18世紀半ごろ、栽培の推進をしたのはプロイセン王のフリードリッヒ大王である。また、同じころ、アイルランドでは小作農家がジャガイモの栽培を行うようになり、急激にその依存度を高くした。おそらく、この時期に、ジャガイモを利用したコテージパイが食卓に上がるようになったのであろう。

コテージパイはいたって調理が簡単な料理だ。ひき肉を玉ねぎとにんじんと一緒に炒め、その上にマッシュポテトをトッピングして、オーブンで温めるだけだ。料理に使う材料は以下のものだ。

主なものは、牛ひき肉(300g)、ジャガイモ5個、玉ねぎ1個、ニンジン1本だけ、残りは味付け用なので、好みに応じて変えてもよい。

最初に用意するのは、マッシュポテト。ジャガイモの皮をむき、

大きさが均等になるように、1個のジャガイモをそれぞれ12等分する。

今回は、これらをラップして、電子レンジの「茹で根菜」という機能を利用して、調理した。

中まで火が通っていれば、ラップの上に厚い布をかぶせ、指で押せば、マッシュポットができる。今回は、少し硬かったので、中華料理のレンゲの底で押してつぶした。

つぶしている途中で、牛乳大匙2杯、バター10g、塩、黒胡椒をそれぞれ小さじ1/4を混ぜ、マッシュポテトに味付けをする。

玉ねぎ1個とにんじん1本はそれぞれみじん切りにする。

フライパンを温め、オリーブ油をひいて、牛ひき肉を色が変わるまで炒める。

さらに、玉ねぎを混ぜて、これが透明になるまでさらに炒める。

塩小さじ１、黒胡椒を加え、さらにローリエ、ニンジンを加えて、1分ほど炒めた後で、80ccのお湯にマギーブイヨン1個を溶かし、これを加える。
さらに、薄力粉大匙2杯を茶こしを使ってまんべんなくまぶし、トマトペースト(6倍濃縮)を一袋(18g)加えて、水分がなくなるまで、さらに炒める。

にんじん、玉ねぎと一緒に炒めたひき肉を、耐熱皿に移し、平らにする。

その上に、マッシュポテトをのせる。

190度に熱したオーブンで、これを20分間ほど温める。

野菜を付け合わせにして、食卓に出す。今回はインゲンにした。

コテージパイの断面はこのようになっている。

年末の忙しい時期には料理にあまり時間をかけられないので、手間のかからないコテージパイは手ごろな料理である。

今回は、ひき肉に牛を用いたが、イギリスではラムやマトンを用いることもある。この場合には、シェパーズパイ(shepherd's pie)と呼ばれる。トライしてみたいのだが、ラムのひき肉が入手しにくいのが問題だ。

極限－圏論の積

プログラマのための圏論(初級編)では、自然変換まで説明した。ここまで理解すると本当の意味で圏論を自由に扱えるようになる。上級編では、これまでの理解を踏まえて、さらに圏論の奥義を学ぶことにしよう。

１．極限

圏論の特徴は抽象階層だと思う。圏は、対象と射によって構成される構造だ。従って適当に、対象と射を選ぶことによって、圏を作ることができる。下図では、圏\(\mathcal{B}\)は、対象\(A,A’\)と射\(f,f’,f’’\)により構成されている(圏を構成するには、このほかに、合成や恒等射などを必要とするがここでは本質的なものだけで記述する)。

さらに、圏を対象にして、圏と圏との関係を射とすることで、抽象的な圏を作成することができる。この操作を繰り返すことで、より抽象的な圏を得ることができる。

下図では、圏\(\mathcal{B}\)を対象\(B\)にして、新たな圏\(\mathcal{C}\)を構成した。\(B’\)は同じく圏\(\mathcal{B’}\)を対象にしたものである。\(g,g’,g’’\)は圏\(B\)と\(B’\)の間の射である。一般には、\(g,g’,g’’\)は関手と呼ばれ、\(\mathcal{C}\)は小さな圏の圏と呼ばれる。

同じように、圏\(\mathcal{D}\)も構成される。この時、\(h,h’,h’’\)は自然変換と呼ばれる。

逆に、ある圏から、その対象の要素を対象とし、要素間の関係を射とすることで、具体的な圏を作成することができる。この操作を繰り返すことで、より具体的な圏を得ることができる。

対象と射という概念で、抽象階層のどのレベルをも構成できるため、圏の構造はとても規則的で、簡潔であると言える。

圏論では、あらゆる種類の中で成り立っているような普遍的な性質を表現することを一つの目標とする。圏論の教科書を開くと様々な普遍性を見つけることができる。その中で、抽象階層の有用性を教えてくれる普遍性は極限だと思う。中学校では、最大公倍数や最小公倍数などを習ったし、高校では関数の最大値・最小値や無限数列の極限値などを学んだ。これらは、ある性質を有するものの並びの中で、極限にあるものを求めている。

それでは、圏論での極限がどのようなものであるかを見ていこう。極限の説明は、圏での積を用いて行われていることが多いので、ここでも、積を用いて説明しよう。

１．１　圏での積

圏論は、対象を定義しなければならない、ここでは、まず、\(A\)と\(B\)を対象としよう。そして、この積を\(A \times B\)で表すことにしよう。次に、射を定義することにしよう。ここでは、\(A \times B\)から\(A\)への射\(fst\)と\(A \times B\)から\(B\)への射\(snd\)とで表すことにしよう。図で表すと次のようになる。

\(A\)と\(B\)が集合の場合には、積はデカルト積と呼ばれ、それぞれの要素\(a \in A\)と\(b \in B\)の対(a,b)で表すことができる。対として表した時、最初の要素が\(A\)に、二番目のそれが\(B\)に属すという意味で、分かりやすくするために便宜的に、射\(fst\)と\(snd\)を用いた。このため、\(fst\)と\(snd\)である必然性はないので、一般的によく用いられている\(\pi_1\)と\(\pi_2\)であってもよい。

圏で用いられている対象、射、積を漫然と理解したままで次に進むと罠にはまってしまうことが多いので、ここでは、これらの概念を具体的な例を用いて、より詳しく理解することにしよう。

圏での積は、乗算であったり、論理積であったりするが、ここでは、論理積と考えることにしよう。また、対象は、連続的な空間であったり、有限の要素の集合であったりするが、ここでは、まず、有限な要素の集合とする。そして、次のような問題を考えることにしよう。

例題1

「ある学年での\(A\)組のクラスで体育会系の部に属していた男女のペアそれぞれについて、同じ部に属していたかどうかを弁別する」プログラムを考え、先の対象\(A \times B\)を何にしたらよいかを考えることにしよう。

このプログラムは、条件「\(A\)組のクラスで体育会系の部に属していた男女のペア(これは、単一でも複数であってもよいとする)」を満たすもののみ受け付けることでき、そうでない場合には、受け付けず処理を行わないものとする。プログラムが受け付けた場合、同一の体育会系の部に属している場合には\(True\)を、異なる体育会系の部に属している場合には\(False\)を返すものとする。そして、プログラムが受け付けてくれるものを\(A \times B\)の候補ということにしよう。

例えば、\(A\)組テニス部所属\(B1\)君と\(A\)組水泳部所属\(G1\)さんの\(P1=(B1,G1)\)をプログラムに入力したとしよう。二人とも\(A\)組に属し、体育会系の部に属するので、プログラムは受け付けてくれ、\(False\)が返ってくる。従って、\(p1\)は\(A \times B\)の候補である。

次の例はどうであろうか。\(B\)組所属の男子\(b2\)と\(A\)組テニス部所属の女子\(G2\)の対\(P2=(B2,G2)\)をプログラムに入力したとしよう。男子が\(A\)組でないので、このプログラムはこの入力を受け付けない。このため、\(P2\)は候補とならない。

それでは、\(A\)組卓球部所属の男子\(B3\)と\(A\)組ダンス部所属の女子\(G3\)の対\(P3=(B3,G3)\)をプログラムに入力したとしよう。この入力は受け付けられる。このため、\(P3\)は候補となる。

このようなことを繰り返し行ったとすると、いくつもの候補が上がるであろう。その中で、不足することなく条件に合う対となっているのはどれであろうか。\(A\)組体育会系の部に所属する男子\(Bas\)と\(A\)組体育会系の部に所属する女子\(Gas\)の対であることは容易に分かる。

これを図で表してみよう。\(P1\)と\(P3\)と\(Bas \times Gas\)が候補であり、\(A \times B = Bas \times Gas\)が条件を満たす最大の集合であることが分かったので、次の可換図式を得る。図において\(incl\)は包含関数である。

この例で、\(A \times B \)の候補となるのは、\(Bas \times Gas\)の部分集合であることが分かる。

例題2

先の例は離散系であったので、今度は連続した空間での例を挙げることにしよう。ある地域\(R\)の標高と年間平均気温の関係を表すことを考えよう。今、標高の方は赤色で表すことにし、高いほど濃くなるようにした。また、気温の方は黄色で表すことにし、低いほど濃くなるようにした。これらの色は絵の具で混ぜることにした。従って、標高が高く気温が低いほど、橙色は濃くなり、反対の場合には薄くなる。

標高を赤色で表した地域\(R\)の地図を\(A\)とし、年間平均気温を黄色で表した\(R\)の地図を\(B\)とした時、このような地図をその一部でも作成できるようなものを探すこととしよう。前の例に習って、これを\(A \times B\)の候補と呼ぶことにしよう。

\(R\)内のある地点\(R1\)での標高を\(P1_h\)とし、その地点での年間平均気温を\( R1_t\)とした時、\(R1=(R1_h, R1_t\)は、求められている地図の一部を描くことができるので、候補となる。

\(R\)の隣の地域\(R2\)での標高を\(R2_h\)とし、そこの年間平均気温を\( R2_t \)とした時、\(R2=(R2_h, R2_t)\)は、求められている地図の範囲外であるので、候補とはならない。

\(R\)に含まれる小さな地域\(R3\)での標高を\(R3_h\)とし、そこの年間平均気温を\( R3_t \)とした時、\(R3=(R3_h, R3_t)\)は、求められている地図の一部を描くことができるので、候補となる。

\(R\)に含まれる小さな地域\(R4\)での標高を\(R4_h\)とし、\(R\)内の別の地域\(R4’\)の年間平均気温を\( R4’_t \)とした時、\(R4=(R4_h, R4’_t)\)は、求められている地図の一部を描くことができないので、候補とならない。

\(R\)に含まれる小さな地域\(R5\)での標高を\(R5_h\)とし、\(R5\)の年間日照時間を\( R5_s \)とした時、\(R5=(R5_h, R5_s\)は、求められている地図の一部を描くことができないので、候補とならない。

これらの関係を可換図式で示したのが、下図である。

この例でも、\(A \times B \)の候補となるのは、\(R_h \times R_t\)の部分集合であることが分かる。

１．２　積の定義

圏では積は次のように定義される。

\(\mathcal{C}\)を適当な対象\(A,B\)を有する圏とする。\(A\)と\(B\)の積は、\(A \times B\)と書かれる\(\mathcal{C}\)の対象と二つの射\(fst : A \times B \rightarrow A \)および\(snd : A \times B \rightarrow B \)との組で、以下の普遍性を満たすものをいう。

積の普遍性

任意の対象\(X\)(これは例題1，2では候補と呼んでいたもの)および射の対\(p:X \rightarrow A\)および\(q:X \rightarrow B\)が与えられた時、一意的な射\(m : X \rightarrow A \times B\)が存在して、下図

を可換にする。

上の定義から、この圏では、\(A\)と\(B\)への射を有するどのような対象を持ってきたとしても、積の普遍性が満たされる。即ち、\(A\)と\(B\)への射\(p'\)と\(q'\)を有する任意の対象\(X’\)を持ってきたとしても下図のように可換性が成り立ち、一意的な射\(m’ : X’ \rightarrow A \times B\)が存在する。

このことから、このような全ての対象(例題1，2で候補と言っていたもの)の中で、\(A \times B\)が\(A\)および\(B\)への最も優れた射(射の合成として表されないという意味で優れたということにする)を与えることから、極限ともいわれる(ただし、極限はのちの説明ではもっと一般的に使う。候補の中で、どれよりも優れた射を有するものと理解して欲しい)。

理解を深めるためには、次の問題を解くことを勧める。

問題1：例題1をHaskellで実現しなさい。
問題2：例題2をHaskellで実現しなさい。

縄文時代のモラルと家族システム

神奈川歴史研究会の9月の例会で発表した報告書を転載します。

縄文時代のモラルがどのように形成され、どのような家族システムを構築したかについて論じています。

弥生時代の土偶形容器を横浜市歴史博物館に見学に行く

文明の衝突は社会を激震する。律令制や明治維新はその代表的なものだが、弥生時代の到来もそれに劣らない文明の衝突であった。

弥生時代に先立つのは縄文時代である。この時代は、1万年もの長きにわたって続き、人々は狩猟採集の定住生活を享受していた。この当時の人びとは、食糧確保のために費やす時間はそれほど多くはなかったと推察されている。傍証になるが、定住はしなかったが、同じように狩猟採集生活を送っていたオーストラリア先住民のアボリジニの人々は、食糧獲得のために、4時間半程度しか使っていなかった。彼らは、余剰の時間を音楽や絵画に振り向けていたが、縄文時代の人々はどのように振り分けていたのであろうか。

その一端を伺わせてくれるのが、時間をかけて丁寧に作成されたと見られる、土器や土偶である。縄文時代の中期になると、燃え上がる炎をかたどったような装飾性溢れる火焔型土器が出現する。同じころ、長野県の八ヶ岳山麓の遺跡では「縄文のビーナス」と呼ばれる土偶が、後期の初めになるとそこから4㎞離れた地点で「仮面の女神」と称せられる土偶が造られた。また、東北地方でも後期には、合掌土偶や遮光土偶が造られている。

男女間での分業が行われていた縄文時代には、土器や土偶は女性により製作された。得意のおしゃべりをしながら余剰の時間をこれらの製作を通して楽しんだのであろう。他方の男性は余剰の時間をどのようにつぶしたのであろう。これは推察の域を出ないが、食料確保を兼ねながらスポーツとして狩猟を楽しんだのだろうか。

しかし、楽しんでばかりもいられなかった。縄文時代も晩期になると、これまで温暖であった気候は寒冷化し、現在よりも気温で2度程度低下し、縄文集落が集中した信州の山々には深い雪が降り、関東の海岸線は後退して、狩猟採取生活が困難になる。縄文時代最盛の中期には26万人程度の人々が住んでいたが、晩期には8万人程度に落ち込んだ。

縄文の人々が困難を極めている頃、新しい文明がもたらされた。朝鮮半島からの水田稲作技術を携えた人々の渡来である。今から3000年前のことで、九州北部で始まった。

水田稲作で特徴づけられる弥生時代の文化は、狩猟採集による縄文時代のそれとは大きく異なっていた。縄文時代の社会が家族あるいは拡大家族を中心とした共同体であったのに対し、弥生時代は血縁関係を超えた大きな集団が形成され、それを統率するようなリーダーが出現し、社会が階層化し始めるような社会であった。水田稲作は、水田の管理・運営に多大の労力を必要とするだけでなく、従事者間での協力や秩序を必要とする。水田稲作によって、多くの人々は土地に縛られ、離れられない状態になる。他方で、人や水田を管理するような人も現れる。

仲間内で諍いが起きたとき、縄文時代は他の場所に居住地を求めて去れることが容易に行えたが、弥生時代は水田に縛られているため、他の場所に移動することは容易ではなかった。このため、諍いが起こらないようにすることで生じるストレス、そして、諍いが生じたときにそれを解決しようとすることに起因するストレスは、それ以前とは比較にならないほど大きかった。他の言葉を借りるなら、縄文時代とは異質のモラルを弥生時代は必要とした。

さらには、収穫物である米や生産するための水田を狙っての集落の間での収奪も生じる。このため、部族間での対立を解決するための対策や方策も必要とした。

縄文時代は血のつながりを認識できるような人々の集まり、部族社会であったのに対し、弥生時代には、集団を統率する人が現れ、社会が階層化しはじめた。即ち、古墳時代に本格化する首長社会への移行期である。古墳時代になると地方豪族が大きな集団をまとめるようになり、さらに、ヤマト政権が誕生して原始国家が成立するようになる。

残念なことに、水田稲作をいったん始めてしまうと、かつての狩猟採集生活に戻ることはできない。単位面積当たりで獲得できるカロリー量では、水田稲作は圧倒的に勝る。このため、水田稲作を始めてしまうと人口が急増し、狩猟採集では維持できないほど多くの人々が居住してしまい、縄文時代の生活に戻ることは不可能になる。

水田稲作という新しい文明が日本列島に入り込んできたとき何が起きたであろうか。縄文時代の生活を維持していた在地の人々は、水田稲作を携えてやってきた渡来の人びとを、すんなりと受け入れたのであろうか。あるいは、撃退しようとしたのであろうか。逆に、撃退されたのであろうか。

関東地方に水田稲作がもたらされたのは、だいぶたってからのことである。横浜では大塚遺跡が有名であるが、ここに伝わったのは弥生時代中期後葉、2000年前ごろとされている。九州北部にもたらされてから1000年もたってからのことである。水田稲作を生業とする集落は、他集落からの攻撃に備えて、環濠で守られている。環濠は、集落の周りをV字型や逆台形の深い溝(大塚遺跡の場合は幅4.5m深さ2.5m)で囲んだ構造物である。大塚集落は、環濠集落全体が発見された、貴重な遺跡である。

小田原市の中里遺跡は、関東地方では最初期の弥生集落である。大塚遺跡から発見された土器は宮ノ台式土器であるが、この遺跡からはその一つ前の世代の中里式 (須和田式) 土器が出土している。中期中葉と呼ばれる時代に属す。

中里遺跡の北5㎞のところには、弥生時代前期前葉、およそ2500年前、の中屋敷遺跡がある。この遺跡からは炭化米が発見されている。関東地方での水田稲作の到来については解明されていない点が多いものの、この遺跡はこれを研究する上で貴重な存在と考えられている。

中屋敷遺跡は昭和女子大学が発掘調査を行っている。調査に当たっている人たちが女性だけというユニークさも手伝って、興味のある場所である。

ここから発掘された小型の精製品の土器は、縄文時代晩期以降の形式を踏襲しており、縄文文化が根強く残っていることを伺わせる。そして、面白いのは、土偶形容器だ。

先週まで、横浜市歴史博物館で、「横浜に稲作がやってきた」という特別展示が開催され、この土偶が展示されていた。そこで、文明の衝突の一端でも知ることができればと思い、見学に行った。
正面から見ると、

顔の表情が豊かで、入れ墨も施されている。普通の女性なのだろうか、それとも、祭祀と関係のある特別な人なのだろうか。縄文時代の土偶はほとんどが女性だ。この土偶も胸の表現があるので女性だろう。土偶と言えば、縄文時代を代表する遺物で、弥生時代には存在しないと思われているが、そのようなことはな。非常に少なくなるが400体ほど発見されている。その中で、土偶形容器と呼ばれるものもおよそ40体ほど見つかっている。土偶形容器は男女一対で作られることが多いので、対の男性の方はまだ地下で眠っているのだろうか。

上の方から見ると中空の容器のようになっていることが分かる。

容器の中には、骨が入っていたそうで、新生児の骨と鑑定されている。土偶が墓の副葬品として利用されることは縄文時代にはほとんどなかったが、晩期後半には東海地方ではそのように用いた例もあるそうだ。また、この容器の中に新生児といえどもそのまま入れることはできなかったと思われるので、一度埋めた後、その骨を取り出して容器の中に収めたと思われる。縄文時代後・晩期には再葬が広く行われるようになっていたが、その傾向をひくものだろう。また、弥生時代初期には、蔵骨器を用いた壺型再葬墓が発達するがその流れにも沿ったものである。

中屋敷遺跡の状況を見る限り、縄文時代からの継続性を読み取ることができる。また、炭化米の出現が示唆するように弥生文化の到来が近くまで迫っているが、新しい文化からそれほど大きな影響を受けているようには思えない。しかし、水田稲作文化の影響を本格的に受けるのは、この後であろうから、その時、どうであったかについては判断を下すことはできない。

中屋敷遺跡から発見された大型の土器も展示されていた。

これらには弥生時代の条痕文の模様がついている。写真の下の方に小型の土器が写っているが、残念ながら、これらの土器の原形の部分が破片に近かったので写真を撮るには至らなかった(この記事を書いている段階では、縄文時代の模様が記録として残らず残念なことをしたと感じている)。

特別展示を見た後、大塚遺跡も見て回ったので、その時の写真も載せておこう。
環濠はこのようになっている。

竪穴住居跡は、

復元された竪穴住居は、

掘立柱建物跡には高床倉庫が復元されている。

大塚遺跡の規模は2.2ha、竪穴住居の数は85軒、使用された年数は50年程度、各住居跡で3～5回程度建て替えられたと考えると同じ時期に立っていた住居はおよそ20軒、各住居に5人程度住んでいたとすると、同時期の居住者の数はおよそ100人と考えられている。遺跡は、1/3ほど残されていて、夜間を除いて見学できるようになっている。

また、隣接して、歳勝土遺跡がある。ここは、大塚遺跡の人たちの墓地と考えられていて、弥生時代の代表的な墓制の一つである方形周溝墓が30基ほど発見されている。
木棺が埋められた状況が復元されている。

また、墓の全体もわかるようになっている。

関東地方では、立派な土偶を見ることは少ないが、今回は、弥生時代のものとは言え、優れた土偶を見学することができ、とてもよかった。特別展示の入口には土偶形容器が、出口には人面付土器(横浜市上台遺跡)が置かれていた。これは、弥生時代後期のものであった。中期までは再葬墓として用いられていたが、これは集落から発見されたそうで、その用途が変化したのだろう。およそ1000年の弥生時代の変化を知ることもでき、良い展示であった。

都内世田谷区の荏原台古墳群を訪れる

11月3日は晴れの日が多い特異日である。この日は雨が降ると天気予報ではずっと伝えられていたが、前の日になって、急に晴天になると変更された。そのとおり、雲一つない素晴らしい日になったので、前の日の埼玉古墳群に続いて、荏原台古墳群を訪れた。

訪問の一つの理由は、思い出の地だからである。荏原台古墳群は田園調布と野毛の二つの地域に分かれている。田園調布では、駅の近くにある教会で結婚式を挙げたし、短い期間だが生活したこともある。野毛は高校3年生の夏にテニスに明け暮れたところだ。

埼玉古墳群と荏原台古墳群の間には、因縁があるというのももう一つの理由だ。後で詳しく説明するが、荏原台古墳群の豪族が先に台頭し、その後で、埼玉古墳群(あるいはその近く)の豪族が台頭してきて、両豪族の間で、「武蔵国造の乱」が起きたのではないかと見なされている。

それでは、野毛の地域を紹介しよう。ここは、大井町線の等々力駅が最寄り駅だ。景色を楽しむために、等々力渓谷を経由する。夏でもひんやりとしていて、渓谷という名に恥じないところだ。渓谷の様子をいくつか示そう。多くの人が散歩を楽しんでいる。


高校3年生の時にテニスで利用したところは、企業の保養所で半分は建物と庭園、半分はテニスコート3面になっていた。テニスコートは住宅に変わっていたものの、残りの部分は日本庭園として活用されていた。

ここからそれほど遠くないところに、野毛大塚古墳がある。ここは、帆立貝形古墳がある。全長82mで5世紀前半の築造だ。埼玉古墳群に先んじていることが分かる。

この古墳の模型もあった。

等々力駅に戻って、東横線の多摩川駅で下車して、荏原台古墳群のうちの田園調布の地域を訪ねる。多摩川の堤の上にあり、眺めがよい。人気高い住宅街となっている武蔵小杉を望むことができる。

この台地にはかつて調布浄水所があったそうで、跡地は次のようになっている。

しばらく歩くと、亀甲山古墳の案内がある。この地域最大の古墳で4世紀後半から5世紀前半の築造で、全長は107mである。樹木に覆われているため、全容を見ることはできない。

さらに歩くと、多摩川台古墳群1～8号墓の案内がある。

それぞれの墓には、場所を示すだけの板が置かれているだけだ。付近を見ても墓らしい様子を知ることはできない。

しかし、墓とは反対側の田園調布の景色はきれいだ。結婚式を挙げたカトリック田園調布教会も見ることができた。

さらに歩くと、前方後円墳の宝莱山古墳を右手にし、左の方に曲がると宝莱公園になる。公園を出ると、駅へと繋がる銀杏並木がある。

さらに進むと、懐かしい駅舎が現れる。

しかし、この駅舎は駅の業務をしていない。面影だけを残しているモニュメントだ。かつては駅舎の向こう側にはホームがあった。しかし、今は、モニュメントの駅舎を抜けると、本当の駅舎へ向かうための階段が現れる。昔の田園調布の駅前の雰囲気がとても良かったので、その雰囲気を残すために、そのままの姿で残されたのであろう。

歩いたコースの説明が終わったので、荏原台古墳群と埼玉古墳群の関りを説明しよう。

この当時の世界情勢から始めよう。『日本書紀』の継体21年(527)・22年(528)の条には、『筑紫国造磐井』の「叛逆」事件の伝承がある。

この伝承に対して、戦前からこれまで様々な解釈が試みられてきた。今日では、東アジアの国際情勢とのかかわりあいを重視して、「磐井は、この頃、九州の筑紫・火(肥)・豊の諸国に勢力を張り、朝鮮半島の高句麗・百済・新羅諸国と積極的に外交を行い、一つの王国を形成しつつあったことがうかがえる」と見られている(佐藤信)。

当時の日本列島は、「王(キミ)」と呼ばれる地方豪族が存在し、王たちが連合的関係を作り、その中心の王を「大王(オオキミ)」と呼んでいた。大王はのちに天皇になるが、この当時の大王と王の関係は上下関係ではなく、同盟関係に過ぎなかった。

磐井も筑紫君磐井と呼ばれた。君と王とは「キミ」は同音であり、磐井は「王」であった。

磐井の乱と同じように地方豪族との戦いが、同時期に関東にもあったことが伝承されている。これは「武蔵国造の乱」である。『日本書紀』安閑元年(531)閏12月条に記載されているが、そこに、「王」と同音の「君」を用いた、上毛野君小熊が出てくる。大王に対抗できるような王が関東にいたのであろう。『日本書紀』には次のように書かれている。

武蔵国造笠原直使主(オミ)と同族小杵（オギ）と、国造を相争ひて、[使主・小杵、皆名なり。]　年経るに決め難し、小杵、性阻くして逆ふこと有り。心高びて順ふこと無し。密に就きて援を上毛野君小熊に求む。而して使主を殺さむと謀る。使主覚りて逃げ出づ。京に詣でて状を言す。朝廷臨断めたまひて、使主を以て国造とす。小杵を誅す。国造使主、悚憙懐に満ちて、黙已あること能はず。謹みて国家の為に、横渟、橘花、多氷、倉樔、四処の屯倉を置き奉る。

この伝承は、笠原直使主と同族の小杵が武蔵国造の地位を争ったとき、その加勢を、使主は朝廷(大王)に求め、小杵は上毛野君(王)に求めたというものだ。磐井と同じように、上毛野は大君と争うほどの勢力があったことが分かる。また、横渟は横見郡(埼玉県)と、橘花は橘樹郡(川崎市)、多氷は多摩郡(東京都)、倉樔は久良岐郡(横浜市)と比定されている。

滅びてしまった小杵だが、彼はどこに住んでいたのであろうか。二つの説があり、一つは南武蔵(亀甲山古墳や芝丸山古墳など)、他の一つは(比企地方の古墳群)である。なお、使主は埼玉古墳群と比定されている。

埼玉古墳群稲荷山古墳からは鉄剣が出土している。辛亥年と銘があり、471年と531年の説があるが、前者の方が有力である。また、銘文の解釈は一つではないが、中央豪族のワカタケル大王(倭王武)からこの地域の豪族ヲタケに下賜されたというのが有力である(大王が中央豪族ではなく関東の豪族という説がある)。もし、これが正しければ、同盟関係から従属関係へと移行していたことをうかがわせる。

鉄剣を下賜されたヲタケと笠原直使主の関係も明らかではないが、何らかの関係があるとすれば、笠原直使主が朝廷を頼ったこともわかりやすい。

さて、小杵が南武蔵の豪族であったとすると、彼らが残した古墳は荏原古墳群であったと思われる。この古墳群は、先に述べたように、田園調布の地域と野毛の地域に分かれる。

まず、田園調布の地域に、4世紀前半には全長97mの宝莱山古墳が、後半から5世紀前半には全長107mの亀甲山古墳が出現する。これらの古墳は前方後円墳である。この後、この地域には6世紀前半まで、古墳は出現しない。

5世紀になると、古墳の位置は野毛の地域に移動し、全長86mの野毛大塚古墳、全長30mの八幡塚古墳、全長57mの御嶽山古墳が出現し、八幡塚古墳は円墳であるが、残り二つは帆立貝形古墳である。

6世紀になると、再び田園調布に戻るが、古墳は小型である。6世紀前半に小型前方後円墳の浅間神社古墳、6世紀後半から7世紀中ごろにかけて多摩川台古墳8基(二つは小型前方後円墳、残りは円墳)、6世紀末に前方後円墳と思われる観音塚古墳が出現し、7世紀中・後期には古墳は築造されなくなり、横穴墓となる。

小杵が敗れたのは6世紀の前半であるので、この当時田園調布に築造された古墳が小型になる。この点をとらえて、甘粕健は「武蔵における古墳時代の有力古墳の分布が、前期の武蔵南部から後期には武蔵北部(埼玉古墳群)に移動したことも、「武蔵国造の乱」とかかわりがあると指摘している。

このように遠く離れた二つの地域が、歴史の中でつながりがあったことを知るのは楽しいことである。

全国有数規模の埼玉古墳群を訪れる

弥生時代の遺跡を2か所ほど立て続けに訪問したので、それに続く、古墳時代の遺跡を訪ねることにした。

この時代の象徴的な墓は前方後円墳である。前方後円墳と言えば、近畿地方と思いがちだがそうではない。全国に広がっていて、関東地方にもたくさん存在する(前方後円墳が一番多い県はなんと千葉県で約720基存在する)。埼玉県行田市の埼玉(さきたま)古墳群は、全国有数の規模を誇り、10基余りの前方後円墳が集中している。近畿地方には、全長が200mを超えるものが存在する(最大のものは大仙陵古墳で486m)ので、それらには匹敵しないが、ここには100mを超えるものが3基存在する。

10月2日も天気に恵まれたので、電車が空きはじめたころに家を出た。横浜方面から埼玉県へ向けての移動は、新宿湘南ラインができてから、とても便利になった。この日も、渋谷駅まで出た後、そこからは最寄り駅まで一本で行けた。但し、最寄り駅と言っても、古墳群まではかなりある。行田駅から「観光拠点循環コース」を利用すれば古墳群まで運んでくれるのだが、一日7便しか出ていない。どれも都合のよい便ではなかったので、一つ前の吹上駅で降りて路線バスを利用した。

吹上駅からの路線バスでは、佐野経由を利用するとよい(行先表示変化中にシャッターを押したため、表示が明瞭でない)。

残念ながら、路線バスは古墳群には行かない。このため、最も近い停留所「産業道路」で降り、そこから15-20分歩かないといけない。産業道路の一つ前の停留所は「佐野団地」。ここまでは、バスは駅からまっすぐに進んでくる。そして、産業道路の停留所の手前で左折する。バスを降りた後、去って行くバスとは反対方向にひたすらまっすぐ歩いていくと、埼玉古墳群に至る。ここは大きな公園になっている。

全ての古墳を見学するコースは1時間半ほどかかると説明にあった。遠路をはるばるやって来たので、全てを見学することにした。見学した順番ではなく、古墳ができた順に従って説明しよう。

前方後円墳は近畿地方では3世紀ごろに始まり6世紀になると規模が小さくなるが、埼玉古墳群はこれとは反対に6世紀に盛んになる。

埼玉古墳群の中で最古の古墳は、稲荷山古墳である。時期は5世紀後半である。全長120mの前方後円墳だ。

古墳の頂まで登れるようになっているので、上を目指す。

この古墳からは、後で紹介するが、文字が刻まれそこに金が埋められた鉄剣が出土している。下の写真のように埋葬されていたそうだ。

二子山古墳は6世紀前半に築造された。全長138mの前方後円墳で、埼玉古墳群の中では最も大きい。古墳の一部が損傷しているということで、修復工事が行われていた。

丸墓山古墳も6世紀前半に築造された。ここの古墳群の中では唯一の円墳で直径105m、日本最大規模の円墳である。1590年の小田原征伐の時に石田三成が忍城攻略のために陣を張った場所としても有名である。また、古墳に沿って半円形に石田堤が掘られている。写真の中で、手前に茶色に帯びたすすきがあるが、そのあたりである。

瓦塚古墳も6世紀前半の前方後円墳である。資料館のそばにあり、全長は73mである。

奥の山古墳は6世紀中ごろ、全長70mの前方後円墳である。

愛宕山古墳は6世紀中ごろに築造され、全長63mで最も小さい前方後円墳である。

鉄砲山古墳は6世紀後半の前方後円墳で、全長は109mである。二子山、稲荷山古墳に次いで大きい。

将軍山古墳は6世紀末、全長90mの前方後円墳である。古墳には埴輪が配置され、往時の姿を彷彿とさせている。

また、「将軍山古墳展示館」があり、古墳の内部に入れるようになっている。石室の側壁には房州石が使われ、千葉県の富津市あたりから運ばれてきたものとみなされている。

内部には埴輪も展示されている。

さらに埋葬の様子も分かるようになっている。

中の山古墳も6世紀末の前方玖円墳で、全長は79mである。

最後に紹介するのがさきたま遺跡の資料館だ。ここには、国宝がいくつも紹介されている。その中でも、一番貴重なのは稲荷山古墳から出土した、金錯銘鉄剣だ。

鉄剣の表と裏には金の文字で、鉄剣の由来が書いてある。それによれば、辛亥の年(471年)に、この刀はワカタケル大王(雄略天皇)からヲタケに贈られた。ヲタケの祖先は代々、杖刀人首(じょうとうじんしゅ、親衛隊長)を務めていた。そして、ヲタケはワカタケル大王に仕え、天下を治める補佐をしていたと記されている。これより、ヤマト王権の力が、東国関東にまで及び、この地方の豪族と同盟関係あるいは主従関係にあったことが分かる貴重な資料である。

展示室は、蛍光灯の光が邪魔をして、撮影するには不向きな環境であったが、国宝の大刀、鉄剣、鉄鏃、帯金具、辻金具、鉸具(かこ)、画文帯環状乳神獣鏡、銀環、勾玉などの国宝が整然と展示されていた。

また、埴輪も展示されていた。

小春日和に恵まれたこの日、広場では、幼稚園児や小学生たちが、遠足なのだろう、広々とした芝生の上を楽しそうに走り回っていた。弥生時代の子供たちもこのように戯れていたのだろうかと思いを巡らしながら、電車が混まないうちに少し早めに帰宅への途に就いた。

東海地方の人びとが通り抜けた弥生時代の神崎遺跡を訪ねる

弥生時代後期の相模の国(神奈川県西部)の遺跡では、東海地方の特徴を持つ土器が多く発見され、この地方との文化的な交流や人的な移動があったことをうかがわせる。特に、神崎遺跡はその傾向が顕著で、東海地方の人々が、200Kmという海路を渡ってきたと見なされている。しかも、短い期間、居住しただけで、すぐに誰もいなくなっている。

神崎遺跡はこのように珍しい特徴を有しているので、見学して確認したいと思うようになり、11月1日に訪れた。

この遺跡は、神奈川県の綾瀬市にある。前回訪れた海老名市温故館の南4.5Kmの場所だ。

相模川支流の目尻川が近くを流れ、相模野台地の上に立地している。下の写真で、左側に遺跡、道の右下を目尻川が流れている。川に沿った沖積地の標高は13m、遺跡の標高は24mである。前回紹介した海老名市の川原口坊中が低地で湿地にあったのに対し、神崎遺跡は台地に位置している。洪水などの自然災害に遭いにくいので、居住場所としてはこちらの方が優れていると言えるだろう。しかし、不思議なことに、後で述べるように、短い期間しか使われなかった。

神崎遺跡は、東海地方の人々と特別な関係があったことが認められ、2011年に国の史跡に指定された。2016年には資料館が完成し、今年4月より公園が一部公開され、来年の4月には完成する予定になっている。資料館はこじんまりとまとまっていて、1階と2階に展示室があり、1階は綾瀬市の歴史を、2階は神崎遺跡を紹介している。

公園は、4月の完成に向けて、最後の整備を行っていた。

資料館の玄関には、この遺跡で発見された土器の中で最も大きな壺が展示されている。

神崎遺跡の情報を得るために、2階に上がる。床をこたつのようにくりぬいて、その低面に東海地方から移住してきたことを強調する絵が描かれていて、床に張られたガラス面を通して見られるようになっていた。

2階の展示室は、壁面に説明があり、その前に土器が置かれていた。東海地方からの移住を説明している所の壁面は次のようになっていた。

その前には、下の写真の土器が飾ってあった。

壁面の説明によると、東海地方(静岡県西部から愛知県東部)の土器と在地の土器は、模様のつけ方が異なるそうだ。東海地方の土器は竹串でこすって模様をつけていた(櫛描文)。これに対し、関東地方では、拠り紐を転がすことで模様をつけていた(縄文)。出土土器の95％は東海地方の特徴を持っていたので、在地の人が作ったのではなく、東海地方の人が作ったとされ、また、使用されている粘土が在地のものであることから、東海地方の技術で、この地で製造されたと見なされている。さらに、住居も縦長型の関東地方とは異なり、横長型の東海地方の形をしていることも東海地方の人が移住してきたことを裏付けている。

東海地方の人が相模の地に移住した理由は、この時期(2世紀)は、西の方では戦いが多かったので、(それから逃れるために)集団で移住してきたのだろうと説明されている。

また、神崎遺跡は、この人々が集落を作る前までは無人であった。また、家の建て替えも1回ぐらいしか行われていないので、移住後あまり年月を経ないうちに、人々はいなくなった。突然、遠い地域から現れ、あっという間にいなくなってしまった。なぜ、この地を選んで、そして、捨てたのだろう。色々なことが考えられてミステリーに富んだ遺跡である。

一回り2階の展示室を見た後、工事中の公園を見学した。今度の連休に環濠を発掘する様子を公開するということで、その準備がなされていた。

また、新築の竪穴式住居も見学者の訪問を待っていた。

この地で生活した人々は、素晴らしい景色の中で生活したのだろうと羨ましく思った。できれば、このような牧歌的なところで一度は暮らしてみたいと思いながらこの地を後にした。

海老名市温故館に「弥生時代のムラ」を見に行く

台風一過のこの日(10月30日)、恵まれた天気の中、神奈川県海老名市の温故館を訪れた。

温故館の建物は、大正17年に海老名村役場庁舎として建てられたものを、相模国分寺跡後に移築されたものだ(移築は平成22年に始まり完成したのは翌年)。木造建築で、窓枠の濃い緑色と、壁面の白色のコントラストが鮮やかな洋館だ。

ここで、「大山を望む弥生のムラー河原口坊中遺跡展」が開催されていたので、相模川沿いの弥生遺跡を知りたくて訪問した。

海老名市は神奈川県の中央部に位置する。この地域は、圏央道、新東名などの大型土木工事が盛んにおこなわれたために、数多くの遺跡が発見されている。河原口坊中遺跡もその一つで、圏央道の建設に伴って調査されたもので、弥生時代前期から古墳時代まで続く期間の長い遺跡である。

上図に示すように、相模川に沿った場所に立地し、中津川と小鮎川が相模川に合流する地点にある(二つの川はこの図では、右側にある細い二つの川である)。海老名市のホームページには、下図の海老名市の地形分類図が掲載されている(元図は小中学生の副読本『海老名の大地』)。

海老名市は、西側に相模川が流れ、川に沿って黄色で示されている自然堤防がある、その後背地は湿地となっている。ここまでが低地で、その後ろには、相模野台地が広がっている。緑色の部分がそれにあたる。さらに一段と高くなった場所に丘陵がある。この間の段差は10mを越えている。河原口坊中遺跡は自然堤防あるいは後背湿地の場所にある。

後背湿地の部分は戦前までは沼地で、一歩足を踏み入れるとずぶずぶと沈んでいくようなところで、この場所で水田作業をする人は大きな田下駄をはいたそうだ(温故館の2階に田下駄が展示されている)。

河原口坊中遺跡が湿地に立地したおかげで、この当時使用された道具が水を含んだ土に閉じ込められ、空気に触れない環境にあったため、今日まで原形をとどめて保存されていた。このため、この遺跡展では当時使われた木工具が中心となっていた。そのうちのいくつかを紹介しよう。最初は、米を利用していたことを示す臼と杵である。

農耕具の一つ、土をならすために利用したであろうエブリ。

水田作業の時に、沈み込むのを避けるために利用したであろう田下駄。

木製品の高坏。

高床式住居の上り下りに使われたであろうはしご。

発掘したときは肌色に近い色をしてたが、空気に触れたために黒くなってしまった編みかご。

今回の展示の主役は板状鉄斧である。これと同じようなものは朝鮮半島南部で多く見られ、日本列島では西日本に限られているため、貴重品である。空気に触れることがなかったため、錆びずに保存されていた。

また、小銅鐸も展示されている。神奈川県では3つしか発見されていない。西日本では大きな銅鐸は墓の副葬品として用いられるが、この銅鐸は竪穴住居跡から発見されたとのこと。日常生活の中で使っていたのであろう。

土器も展示されていた(下図は主に弥生時代後期のもの)。

神奈川県の土器形式は図に示すように変化している(展示用のパンフレットの弥生時代の神奈川県域の編年表によっている)。

弥生は、水田稲作が始まった時代である。神奈川県で最初に水田稲作が始まったのは、足柄上郡の大井町にある中屋敷遺跡である。水田の跡は見つかっていないものの、炭化米が見つかっており、AMS法による放射性炭素年代測定では紀元前5世紀～4世紀のものであった。このときは弥生時代前期後半に属す。

東日本で最初の大規模な水田稲作が始まった集落は、小田原市の足柄平野にある中里遺跡である。この遺跡は、弥生時代中期中葉のもので、水田跡や方形周溝墓(弥生時代の特徴的な墓)が発見されている。また、在地の中里式の土器に混ざって、東部瀬戸内地方の土器が3％含まれている。その他にも伊勢湾、中部高地、北陸地方、北関東地方、南東北地方の土器が発見されている。これらの土器は、在地の粘土と異なることから外から持ち込まれたと見なされ、これらの地域との交流あるいは人の動きがあったともみなされている。

河原口坊中遺跡では、後期になると、東海、中部高地、東京湾地域の土器が多く見られるようになり、その後、時を経るにしたがって在地化していく。このため、後期の時代に外部の人たちとの交流があったと見なせる。さらに進んで、遺跡が一時途絶えているので、外部から人々が移住してきたとも考えられる。

この遺跡で面白いのは、魚を追い込むためのしがらみ状遺構があることだ。食料を得るために、いろいろな工夫をしたことと思う。
また、環状石器もたくさん発見されている。環状石器の穴に棒を通せば、「はじめ人間ギャートルズ」が持っていた武器を想像させてくれる。

展示の方はこれくらいにして、国分寺跡を見学した。温故館には国分寺の模型がある。

相模国分寺の伽藍配置は法隆寺のそれと同じである。多くの国分寺が東大寺の伽藍配置(大門、中門、金堂、講堂が一直線に並び、両翼に塔)とは異なり、金堂と塔が左右に並んでいる。この配置を取るのは他に上総国分寺だけだ。温故館を出ると目の前は、国分寺跡である。ここは台地の上にあるので、河原口坊中遺跡のように水に悩まされることはない。塔の跡では幼稚園児たちが遊んでいた。

広々とした公園になっていて、子供たちを遊ばせるのにちょうどいい。

当日はお客さんも我々だけで、説明員の方から丁寧な説明を受けて、楽しむことができた。子供の頃には、温故館のような大正時代の洋風な建物を、小学校や図書館など公立の建造物で多く見かけた。老朽化に伴ってこれらは建て替えられてしまったのであろう。今ではあまり見かけることができなくなってしまった。温故館のように保存されていると、子供の頃の懐かしい思い出がよみがえってくるので、是非、これからも長く保存して欲しいと願いつつ、帰路についた。

日の名残り―The remains of the day

今日、紹介する映画は、『日の名残り』(The Remains of the day)だ。今年度のノーベル文学賞に輝いたカズオ・イシグロの同名の小説を映画化したものだ。1993年の作品で、アカデミー賞の8部門にノミネートされたが、残念ながら、受賞には至らなかった。ちなみに、この年の作品賞には『シンドラーのリスト』が選ばれた。小説としての『日の名残り』は、1989年に発表され、同年にブッカー賞を受賞している。

ストイックともいえるほどに職務に忠実な執事の日常生活を淡々と描いた作品で、アンソニー・ホプキンズがその役を演ずる。

古いタイプの人間を描いたと言えばそれまでなのだろうが、新しく雇った女中頭のケントン(エマ・トンプソンが演じる)に淡い恋心を抱きながらも、ケントンが誘い掛けてくる言葉にも、執事としての対応しかできない、不器用な初老の執事スティーブンスの物語である。

日本には「道」というのがある。武士道、茶道、華道などだ。一つのことを究めようとする精進がそれぞれで問われる。ホプキンズが演じる執事も、執事としての道に精進しているのであろう。昨年、一流大学を卒業し、有名な航空会社で実績を上げていたにもかかわらず、禅僧となった方に、鎌倉の円覚寺を案内してもらう機会があった。境内を案内してくれる道すがら、なぜお坊さんになったのか、僧になるための修業はどのようなものだったのかを語ってくれた。禅の道を究めようとする姿が、執事の姿と重なった瞬間、この映画がさらに好きになった。

作品の内容については映画の方を見て欲しいが、好意に感謝しながらも、それを素直に表現できない無骨さが表れている部分を紹介しよう。

スティーブンスが執事をしている貴族の館でキツネ狩りをする場面がある。

このとき、女中頭として働くことになるケントンは、面接試験を受けに来る。

無事面接に合格したケントンは仕事を始める。スティーブンスの殺風景な個室を明るくしようと考えて、庭先の綺麗な花を摘む。

そして、執務室を訪れ、花を飾りながら、次のように言う。
"I thought these might brighten your parlour."

現在のことを言っているのに、過去形が使われている。高校時代に習った「仮定法過去」という文法の用語を思い出す人もいるだろう。

日本でも、ファーストフード店などに行くと過去形で応対されることがある。慣れていないと面食らってしまう。先日も、オーダーが済んだ後の確認で、「ご注文は以上でよろしかったですか」と言われた。

丁寧さを表すために過去形を用いている。日本語には丁寧語、謙譲語、尊敬語が備わっているので、お客さんとの対応にはこれらの言葉を使えばよい。しかし、ファーストフード店のように仕事を定型化したいところでは、状況に合わせての対応を嫌う。そこで、マニュアル化するために、何とも不思議な言い回しが生まれたのだろう。

英語では、可能性が含まれるような状況を述べるときは、ファーストフード店のような言い回しが普通だ。ケントンがスティーブンスに向かって、「この花が部屋を明るくしてくれますよ。」というのは、あまりにもフランクすぎる。時代は戦前のイギリスで、場面は貴族の館であれば、かつての日本語ではないが、状況に応じた適切な表現が要求される。

mightにはいくつかの使い方があるので、Collinsの"English Grammar"で確認した。4章の「ありそうなことを示唆する」という項目の中の4.137に、可能性として使われる'could','might','may'というのがある。これらの単語は「あることが生じる可能性があるときに」用いると説明がある。例文には、
They might be able to remember what he said.
というのがある。

これらを踏まえると、上の訳は
「お花が執務室を明るくしてくれたらと思ってお持ちしました。」
でどうだろうか。

ケントンの思いがけない行為に面食らって、スティーブンスは次のように言う。
"Beg your pardon?"
この言い回しも、思い出の深い言い回しだ。留学して初めてホームステイをした時、アメリカ人の夫婦の会話の中でしょっちゅう"I beg your pardon."というのを聞いた。日本だと相手の言っていることを聞き直すのは失礼だと考えて、少し前にはやった「忖度をして」、行動しがちだが、彼らは、意味を取り違えないように頻繁に確認を取っていたのがとても印象的だった。

ここは、
「何て言われましたか？」
だろうか。

ケントンは少し表現を変えて、温かみを持たせて次のように言う。
"They might cheer things up for you."
「お花が、周りのものを生き生きとさせてくれ、あなたも明るく仕事ができるのではと思いまして。」

スティーブンスはありきたりな表現で、
"That's very kind of you."
「ご親切に、どうもありがとう。」

ケントンは、スティーブンスの意図を解さないのか、提案を示す"If you like"と"could"(Collins 4.187)を用いて
"If you like, I could bring in some more for you."
「よろしければ、もっとお持ちします。」

スティーブンスは自分のプライベートな生活に入り込まれることを嫌って、
"Thank you, but I regard this room as my private place of work and I prefer to keep distractions to a minimum."
「そのように気を使って下さってありがとう。しかし、この執務室は仕事をするための私の個人的な場所なので、気を紛らわすようなことは最小限にしたいと心がけていますので。」

ケントンは思いがけないことを言われたので、少し攻撃的になって、丁寧を表す"would"を使うが内容は強い表現で、
"Would you call flowers a distraction, then?"
「この花が気晴らしだというの。」

スティーブンスは、いなして、
"I appreciate your kindness. I prefer to keep things as they are."
「あなたのご親切には感謝しています。でも、このままの方がいいのです。」

この後、スティーブンスは父親の呼び方について注意する。ケントンは再びカチンとくる。その場面の表現も面白いので、映画で確認してください。

プログラマーのための圏論（下）

『プログラマのための圏論』は(上・中)の後の部分をまとめ(下)にしてPDFファイルにしました。参考にしてください。なお、(上)のホームページはこちら。
(中)のホームページはこちら。

モナドの応用

最後に

ノーベル経済学賞を受賞したダニエル・カーネマン教授が一般読者向けに著述した『ファスト＆スロー』を読んだ。本のタイトルからは内容はつかみにくい。副題は「あなたの意志はどのように決まるか？」となっているので、脳科学の本かなと思い違いしてしまいそうだ。英語でのタイトルは、”Thinking, Fast and Slow”となっているので、彼の研究内容をある程度知っている人でない限り、タイトルから内容を読み取ることはやはり難しい。

先週はノーベル賞が発表される時期であったため、カーネマン教授の名前を思い出した人も多いことと思う。特に、今年(2017年)のノーベル経済学者はリチャード・セイラー教授だったので、その関連でカーネマン教授を思い出した人は多いだろう。二人とも行動経済学に大きな貢献をしたことでノーベル賞を受賞している。伝統的な経済学は、経済活動をする人たちが経済合理性を備えているということを前提に、理論を構築していた。これに対し、カーネマン、セイラー両教授とも、人間は合理的にふるまうことはまれで、様々なバイアスがかかって行動することを前提に、新しい経済学の理論を構築した。

経済学賞のため、カーネマン教授は生粋の経済学者だと思いがちだがそうではない。カリフォルニア大学バークレー校で1961年に心理学の博士号を取得し、その後、同大学やプリンストン大学で心理学の教授となっている。心理学と経済学を融合し、独自のプロスペクト理論を確立して、人間の経済的行動を説明し、ノーベル賞を受賞するに至っている。

『ファスト＆スロー』では、二つの架空のキャラクター、二つの人種、二つの自己を用いて、一人の人間がどのように意思を決定するかを説明している。一つのものが二つの性格を持つということは、圏論の「モナドだ」に相当するものだと思って、この本を読んでいくととても面白い。

『ファスト＆スロー』の結論の部分に、それぞれの性格が記述されているので引用してみよう。「二つのキャラクターとは、早い思考をする直感的なシステム１と遅い思考をする熟考型のシステム2であるシステム2はシステム1の監視を引き受け、限られたリソースの中でできる限りの制御を行う。二つの人種とは、理論の世界に住む架空の人種エコンと、現実の世界で行動するヒューマンである。二つの自己とは、現実を生きる「経験する自己」と、記憶を取り選択する「記憶する自己」である」と言っている。

システム1と2は、「XXが自動的に起きた」ということを「システム1がXXした」と、「興奮度が高まり、同行が開き、注意力が集中してXXが行われた」ということを「システム2が呼び出してXXが行われた」と言うように、分かりやすく説明するために使われた架空のものである。将棋の藤井4段が、複数人のアマを相手に将棋を指しているときは、システム1を用いてヒューリスティックに駒を置いている。それに対して、トップ棋士と対戦しているときは、システム2を用いて、アルゴリズムをフルに機能させて、勝利へ導く手順を探している。

二つの人種では、エコンは経済合理性に従って行動する自分である。それに対して、現在置かれている環境に影響されて、経済合理性には適わない行動をとるのがヒューマンである。例えば、大きな負債を抱えているときに、それを取り返すために起死回生を狙って大博打をし、結局、損をするのがヒューマンである。

ロマンスの破局は、振る側と振られる側に分かれる。どちらもわかれという面では変わらないのに、精神的なダメージは振られる側が大きい。「逃がした魚は大きい」という喩えもあるがこれも同じようなものだ。もし、ロマンスの期間を細分して、それぞれの時点での幸福度を記憶していたとすれば、振った側も振られた側もそれほど変わらないだろう。しかし、このようなことは忘れてしまい、破局の瞬間だけが記憶に残るようだとすると、振った側と振られた側の衝撃には大きな差がある。「終わりよければ全てよし」という諺があるが、これも同じようなことを伝えている。

モナドとこれらの関係を図で示すと図のようになる。

モナドの世界では、\(A\)の世界を純粋な世界と解釈し、\(M(A\)の世界を現実の世界と見なした。これをカーネマン教授のモデルと対応させると、純粋な世界\(A\)はシステム2、エコン、記憶する自己に相当し、現実の世界\(M(A)\)はシステム1、ヒューマン、経験する自己に相当する。とても理にかなった対応で面白いと思う。このように、全く関係なかったと思われる世界がつながるとき、とても嬉しくなる。

圏論もHaskellも奥の深い学問分野である。圏論だけで理解することも難しいし、Haskellだけで理解することも難しい。しかし、両方を一緒に勉強することで、理論と実践の両面を同時に見ることができるようになる。これによって、両方の分野をより正確に知ることができる。このブログでは、図やプログラムをたくさん掲載し、可視的に、具体的に理解できるように試みた。

今回の記事で、「プログラマのための圏論」はひとまず終了である。お付き合いいただきありがとうございました。

モノイドーモノイド圏での記述

１３．４　モノイド圏での記述

前回の記事で、二項演算を表すための小さい圏の圏(category of small categories)を次のように表した。

この図において、\(f,g\)や\(M(f),M(g)\)などは小さい圏の圏の構成要素には含まれていないので、これを省略することにしよう。

顔がない間延びした図で、少し恐ろしさを感じるが、ここまで来ると、それぞれを構成していた具体的な要素が消失し、抽象化がかなり進んだと認識できるだろう。アセンブラ言語での記述から高級言語への記述へと変化した瞬間を感じ取ることができる。

それではこの図を用いて二項演算、即ち、モノイドを定義してみよう。

二項演算は、同じ対象から二つの値を得て、その間で演算を施し、やはり同一の対象に属す値を結果として返す。これは、圏論では双関手によって表すことができる。このクラスはHaskellでは次のように定義されている。

class Bifunctor p where
  bimap :: (a -> b) -> (c -> d) -> p a c -> p b d

上の定義で、二項演算子を\(\otimes\)と表すならば、\(p\)は\((\otimes)\)と書き直してもよい(二項演算子の中で最も汎用的な演算子はテンソル積であり、テンソル積は( \( \otimes \) )と表される。ここでは、最も汎用性のある演算子を表しているという意味で( \( \otimes \) )を用いた)。

そこで、\(bimap\)の対象を自己関手で置き換えと、次のように表すことができる。
\(bimap :: (F \rightarrow F') \rightarrow (G \rightarrow G') \rightarrow (G \circ F \rightarrow F' \circ G') \)
上の定義で、\((F \rightarrow F'),(G \rightarrow G'),(G \circ F \rightarrow F' \circ G') \)は自然変換で、\(\circ\)は関手の合成で、\(\otimes\)と見なせるものである。上の式を可換図式で表すと、以下のようになる。

ところで、モノイドの定義はHaskellでは次のようになっていた。

class Monoid m where
  mu :: m -> m ->  m
  eta :: () -> m

これを、\(m\)と\( () \)を小さい圏の圏で用いた自己関手\(M\)と恒等な自己関手\(I\)とし、二項演算子\(\otimes\)を用いて、図で表すと下記のようになる。

これをまとめて一つの可換図式で示すと下記のようになる。

モノイド圏を説明するための準備が整ったが、ここでは、Haskellのプログラムで具体的な例を見て、モノイド圏を定義するための準備をしよう。

１３．５　Haskellで記述する

はじめに、前回の記事で説明した小さい圏の圏をHaskellで用意しよう。

ここで作るプログラムは、乗算を演算子として持つモノイドである。

\(\mathcal{A}\)を\(n\)とし、\(M(\mathcal{A})\)を\(Product \ n\)とした時に、\(new type\)を用いて\(Product \ n\)を用意しよう。

newtype Product n = Product n deriving (Eq, Ord, Read, Show)

\(Product\)は\(n\)から\(Product \ n\)を導き出す関手である(小さい圏の圏を説明したときの\(M\)に相当)。そこで、これを\(Functor\)のインスタンスとして定義する。さらに\(Product (Product \ n)=Product \ n\)を満たすので、これを\(join\)という関数で定義しておこう。

instance Functor Product where
  fmap f (Product x) = Product (f x)
  
join (Product (Product x)) = Product x

さて、次に小さい圏の圏を作る作業に移ろう。この圏では射を関手としていたので、これを表すようなデータ型を用意しよう。その名前を\(Pfunctor \ x \ y\)とする。ここで、\(Pfunctor\)は、\(x\)を入力、\(y\)を出力とする関数である。また、この関数からの出力を得られるように\(run Pfunctor\)を用意しておこう。

newtype Pfunctor x y = Pfunctor {runPfunctor :: x -> Product y}

また、小さい圏の圏のクラスは次のように定義する。ここでは、恒等射と合成の関数を定義することにする。

class Category cat where
  id :: cat a a
  (.) :: cat b c -> cat a b -> cat a c

\(Pfunctor\)を小さい圏の圏のインスタンスにしよう。

instance Category Pfunctor where
  id = Pfunctor (\x -> Product x)
  (Pfunctor f) . (Pfunctor g) = Pfunctor $ join Prelude.. fmap f Prelude.. g

それでは、\(Pfunctor\)をクラス\(Monoid\)のインスタンスとして定義しよう。
HaskellのPreludeでは、\(Monoid\)は\(mempty,mappend\)を用いて定義されているが、ここでは前々回の記事で紹介したように、,\(\mu\)を用いることにしよう。

class Monoid' m where
  mu :: m -> m ->  m
  eta :: () -> m

instance Monoid' (Pfunctor x x) where
  eta () = Pfunctor (\x -> Product x)
  mu f g = Pfunctor (\x -> runPfunctor (f Pfunctor.. g) x) 

上のインスタンスの定義の中で、関手\(f,g\)は、\(f=g\)であり、\(f \circ f=f\) を満たさなければならない。

そこで、\(mu\)を直接使うのではなく、同一の関手を使うようにするため、次の\(mu'\)を用意する。

mu' f =  mu f f

また、\(f \circ f=f\)であることを確認するために、\(f \circ f\)と\(f\)で同じ値が得られるかをチェックし、同じであれば出力し、違っていれば出力しないようにしよう。そのために次の関数\(getResult\)を用意する。

getResult f (x,y)
  | a == b = Just a
  | otherwise = Nothing
  where
    a = runPfunctor (mu' f) (x*y)
    b = runPfunctor f (x*y)

\(n\)で割った時の剰余と、絶対値を出力する関手\(modular,abosolute\)を次のように用意しよう。これは、\(f \circ f = f\)の条件を満たしている。

modular :: (Integral y) => y -> Pfunctor y y
modular n = Pfunctor (\x -> Product (mod x n))

absolute :: Pfunctor Integer Integer
absolute = Pfunctor (\x -> Product (abs x))

それではこれを用いて、二つの数\(x,y\)を入力し、\(F x \otimes F y\)を求めてみよう。

*Pfunctor> getResult (modular 5) (34, 67)
Just (Product 3)
*Pfunctor> getResult absolute (12, (-9))
Just (Product 108)

最初の実行例は、入力34,67の5の剰余を求め、その乗算を行うものだ。34の剰余は4であり、67の剰余は2である。従って、4と2の乗算結果は8であるが、これも5の剰余での乗算を行うので、結果は\(Product \ 3\)である。正しい答えであることが分かる。

１３．６　モノイドを圏にする

それでは、これまで説明してきたモノイドを圏の形でまとめてみよう。この圏は自己関手を対象とし、自然変換を射としているので、次のように定義できる。
1) 対象：関手の集まり\(\{M,I\}\)
2) 射：自然変換\(\mu\)
3) ドメイン・コドメイン
4) 恒等射：自然変換
5) 合成：\(\circ\)

この圏が結合律、単位律を満たしていることを可換図式で確認してみよう。ここでは、\(M \circ M\)を\(M^2\)で表す。

ここまでの説明はモノイドの基本的な骨格を元に圏を定義したが、一般にモノイド圏はテンソル積を用いて次のように定義されている。

モノイド圏(\( \mathcal{C}, \otimes, I, α, λ, ρ \))とは、圏 \(\mathcal{C} \)が次の条件を備えているときである。
1) テンソル積と呼ばれる双関手\(\otimes : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C} \)
2) モノイド単位(あるいは単位対象)\(I\)
3) 結合律：\(α_{A,B,C}: (A \otimes B) \otimes C \cong A \otimes (B \otimes C)\)　(ただし、\(α\)は自然同型)
4) 右単位律：\(λ_A : I \otimes A \cong A \), 左単位律：\(ρ_A : A \otimes I \cong A \)　(ただし、\(λ, ρ\)は自然同型)

そして、モノイド対象( \( M,μ,η\))とはモノイド圏(\( \mathcal{C}, \otimes, I, α, λ, ρ \))が与えられたときのその対象である。そしてそれぞれの対象は、\(\mathcal{C}\)の対象\(M\)および二つの射(\(μ : M \otimes M \rightarrow M, η: I \rightarrow M \))を有し、上記の可換図式を満たすものとする。

従って、ここで説明してきたものは、合成\(\circ\) をテンソル積\(\otimes\) で置き換えれば、モノイド対象となる。

１３．７　モナドはモノイド？

この圏の定義も、結合律、単位律の可換図式もどこかで見たことはないだろうか。そう、\(M\)を\(T\)で置き換えれば、モナドを説明した記事と同じものだ。このことから次のことがいえる。

「モナドは、自己関手の小さい圏の圏で記述されたモノイドと同じ」と言える。

これは重要な定理である。

最後に用いたプログラムのリストをつけておこう。

instance Functor Product where
  fmap f (Product x) = Product (f x)
  
join (Product (Product x)) = Product x

newtype Pfunctor x y = Pfunctor {runPfunctor :: x -> Product y}

class Category cat where
  id :: cat a a
  (.) :: cat b c -> cat a b -> cat a c

instance Category Pfunctor where
  id = Pfunctor (\x -> Product x)
  (Pfunctor f) . (Pfunctor g) = Pfunctor $ join Prelude.. fmap f Prelude.. g

otimes :: (Num n) => (Pfunctor a n, Pfunctor a n) -> (a, a) -> Product n
otimes (Pfunctor f, Pfunctor g) (x, y) = Product c 
  where 
    Product a = runPfunctor (Pfunctor f) x
    Product b = runPfunctor (Pfunctor g) y
    c = a * b

class Bifunctor p where
  bimap :: (a -> b) -> (c -> d) -> (p a c -> p b d)

class Monoid m where
  mu :: m -> m ->  m
  eta :: () -> m

instance Pfunctor.Monoid (Pfunctor x x) where
  eta () = Pfunctor (\x -> Product x)
  mu f g = Pfunctor (\x -> runPfunctor (f Pfunctor.. g) x) 
  
mu' :: Pfunctor n n -> Pfunctor n n
mu' f = mu f f

getResult f (x,y)
  | a == b = Just a
  | otherwise = Nothing
  where
    a = runPfunctor (mu' f) (x*y)
    b = runPfunctor f (x*y)

modular :: (Integral y) => y -> Pfunctor y y
modular n = Pfunctor (\x -> Product (mod x n))

absolute :: Pfunctor Integer Integer
absolute = Pfunctor (\x -> Product (abs x))

モノイドー小さい圏の圏での記述

１３．３　小さい圏の圏での記述

これまで、算数で最初に学んだ加算・乗算に代表されるモノイドと呼ばれる二項演算を、圏論でどのように記述したらよいのかについて話を進めてきた。即ち、アセンブラ言語でのように処理を具体的に記述するのではなく、高級言語でのように物事がどのように成り立っているかを構成的に記述しようと試みてきた。これは、モノイドのそれぞれについて具体的に個別に記述を進めるのではなく、モノイドと呼ばれるものが有している性格を抽象的に汎用的に進めようとするアプローチである。前者が技法的なアプローチであるのに対して、後者は科学的なアプローチでもある。

構成を記述する圏論では、構成図を利用することで可視的に計算の概念を示すことができる。モノイドがどのように構成されているのかについて説明するときも、式を展開していくよりは、構成図がどのように変化していくかを示すことで、書き手にとっても、読み手にとても、理解しやすくなる。そこで、ここでは、構成図をうまく利用して、分かりやすい形で求めてみよう。

集合から射へ

前回の記事で、モノイドの例を一つ紹介した。下図での左側がそれである。

ここでは、代数学での記述法に従って、集合\(S=\{0,1,2-\sqrt{3},2+\sqrt{3}\}\)、単位元1、二項演算子\(*\)と表されているものを、圏論での記述に従って、左側の構成図で表した。この図は圏の構成を満たしている。即ち、
1)対象が星
2)射が\(\{0,1,2-\sqrt{3},2+\sqrt{3}\}\)
3)ドメインとコドメインが星
4)恒等射が1
5)合成が\(\times\)
である。また、単位律、結合律は満たされている。

上図の右側は、対象がモノイドであることを、明確にしたものである。数としての\(0,1,2-\sqrt{3},2+\sqrt{3}\)は加減乗除を始めとする様々な二項演算に使われる。そこで、これらが、乗算で用いられることを明確にするために、\(Product\)と呼ばれるコンテナを付与した。右側も、左側と同様に圏であることに注意しよう。このため、圏\(\mathcal{A}\)と圏\(\mathcal{B}\)は関手\(Product:\mathcal{A} \rightarrow \mathcal{B}\)によって結ばれていると見ることができる。

集合の構成要素を一般化して、上図を少しだけ抽象化すると下図を得る。何となく圏論らしくなってきたのが分かるだろう。

右側の圏は、
1)対象が星
2)射が\(\{M(f),M(g),...\}\)
3)ドメインとコドメインが星
4)恒等射が\(id_B=M(id_A)\)
5)合成が\(\circ\)
である。また、単位律、結合律は満たしている。

ここまでの変換で、代数学で集合として表されていたものが、圏では射の集合として表されていることが分かる。でも、集合であることには変わりはない。

小さい圏の圏へ

一般に、小さい圏を対象とし、圏と圏を結ぶ関手を射とする圏を小さい圏の圏(category of small categories)という。もちろん、恒等射と合成を有し、単位律、結合律は満たさなければならない。なお、小さい圏とは、対象と射の集まりがそれぞれ集合となるときを言う。

下図は、
1) 対象：圏の集まり\(\{\mathcal{A},\mathcal{B},\mathcal{C}\}\)
2) 射：関手の集まり\(\{F,G,H\}\)
3) ドメイン・コドメイン：\(\{F :: A \rightarrow B, G :: B \rightarrow C, H :: A \rightarrow C \}\)
4) 恒等射：\(I_A,I_B,I_C\)
5) 合成：\(\circ \)
である。

それでは、二つ前の図を小さい圏の圏\(\mathcal{Cal}\)にしてみよう。恒等射の部分を除くと下図のようになる。

さらに、この小さい圏の圏\(\mathcal{Cal}\)において、\(\mathcal{B}\)から同じように関手\(M\)で\(M(\mathcal{B})\)に接続しよう。

これをさらに行うと、小さい圏の圏は無限に関手\(M\)で結合された圏となる。ところで、元に立ち戻って、\(Product\)で考えると、これは\(x\)を乗算ができる世界へと持ち込んだ。これが、\(Product(x)\)である。これをもう一度乗算ができる世界へ持ち込むと\(Product (Product (x))\)となるが、元々、乗算ができる世界に存在しているので、\(Product (Product (x))=Product(x)\)となる。

そこで、\(Product\)を一般化し、二項演算を行えるようにする関手を\(M\)としたとき、\(M(M(\mathcal{A})) = M(\mathcal{A})\)となる。このため、下図のように表すことができる。

視点を変えるために、\(M\)を外に出るように書いた。このように記述すると、\(M\)は圏\(\mathbf{Cat}\)から\(\mathbf{Cat}\)への関手に見えないだろうか。\(M::A \rightarrow B, B \rightarrow B \)であるので、このような見方は可能である。これは、ある圏から同一の圏への関手であるため、自己関手と呼ばれる。

それでは、この図に、恒等関手\(I\)を追加しよう。

ここで、\(\forall x \in A \cup B, I:: x \rightarrow x\)である。

それでは、二項演算\(M\)のために用意した小さい圏の圏をまとめておこう。
1) 対象：圏の集まり\(\{\mathcal{A},\mathcal{B}\}\)
2) 射：関手の集まり\(\{M\}\)
3) ドメイン・コドメイン：\(M :: A \rightarrow B, B \rightarrow B\)。
4) 恒等射：\(I\)
5) 合成：\(\circ \)
もちろん、単位律、結合律は満足しなければならないが、この他に、二項演算が成り立つようにしなければならない。これについては次の記事で述べる。