プログラマのための圏論(初級編)では、自然変換まで説明した。ここまで理解すると本当の意味で圏論を自由に扱えるようになる。上級編では、これまでの理解を踏まえて、さらに圏論の奥義を学ぶことにしよう。
1.極限
圏論の特徴は抽象階層だと思う。圏は、対象と射によって構成される構造だ。従って適当に、対象と射を選ぶことによって、圏を作ることができる。下図では、圏\(\mathcal{B}\)は、対象\(A,A’\)と射\(f,f’,f’’\)により構成されている(圏を構成するには、このほかに、合成や恒等射などを必要とするがここでは本質的なものだけで記述する)。
さらに、圏を対象にして、圏と圏との関係を射とすることで、抽象的な圏を作成することができる。この操作を繰り返すことで、より抽象的な圏を得ることができる。
下図では、圏\(\mathcal{B}\)を対象\(B\)にして、新たな圏\(\mathcal{C}\)を構成した。\(B’\)は同じく圏\(\mathcal{B’}\)を対象にしたものである。\(g,g’,g’’\)は圏\(B\)と\(B’\)の間の射である。一般には、\(g,g’,g’’\)は関手と呼ばれ、\(\mathcal{C}\)は小さな圏の圏と呼ばれる。
同じように、圏\(\mathcal{D}\)も構成される。この時、\(h,h’,h’’\)は自然変換と呼ばれる。

逆に、ある圏から、その対象の要素を対象とし、要素間の関係を射とすることで、具体的な圏を作成することができる。この操作を繰り返すことで、より具体的な圏を得ることができる。
対象と射という概念で、抽象階層のどのレベルをも構成できるため、圏の構造はとても規則的で、簡潔であると言える。
圏論では、あらゆる種類の中で成り立っているような普遍的な性質を表現することを一つの目標とする。圏論の教科書を開くと様々な普遍性を見つけることができる。その中で、抽象階層の有用性を教えてくれる普遍性は極限だと思う。中学校では、最大公倍数や最小公倍数などを習ったし、高校では関数の最大値・最小値や無限数列の極限値などを学んだ。これらは、ある性質を有するものの並びの中で、極限にあるものを求めている。
それでは、圏論での極限がどのようなものであるかを見ていこう。極限の説明は、圏での積を用いて行われていることが多いので、ここでも、積を用いて説明しよう。
1.1 圏での積
圏論は、対象を定義しなければならない、ここでは、まず、\(A\)と\(B\)を対象としよう。そして、この積を\(A \times B\)で表すことにしよう。次に、射を定義することにしよう。ここでは、\(A \times B\)から\(A\)への射\(fst\)と\(A \times B\)から\(B\)への射\(snd\)とで表すことにしよう。図で表すと次のようになる。
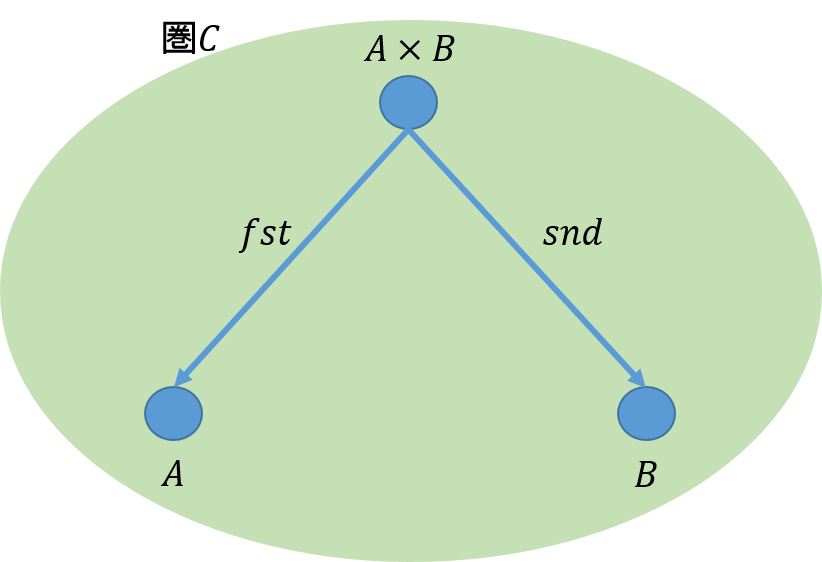
\(A\)と\(B\)が集合の場合には、積はデカルト積と呼ばれ、それぞれの要素\(a \in A\)と\(b \in B\)の対(a,b)で表すことができる。対として表した時、最初の要素が\(A\)に、二番目のそれが\(B\)に属すという意味で、分かりやすくするために便宜的に、射\(fst\)と\(snd\)を用いた。このため、\(fst\)と\(snd\)である必然性はないので、一般的によく用いられている\(\pi_1\)と\(\pi_2\)であってもよい。
圏で用いられている対象、射、積を漫然と理解したままで次に進むと罠にはまってしまうことが多いので、ここでは、これらの概念を具体的な例を用いて、より詳しく理解することにしよう。
圏での積は、乗算であったり、論理積であったりするが、ここでは、論理積と考えることにしよう。また、対象は、連続的な空間であったり、有限の要素の集合であったりするが、ここでは、まず、有限な要素の集合とする。そして、次のような問題を考えることにしよう。
例題1
「ある学年での\(A\)組のクラスで体育会系の部に属していた男女のペアそれぞれについて、同じ部に属していたかどうかを弁別する」プログラムを考え、先の対象\(A \times B\)を何にしたらよいかを考えることにしよう。
このプログラムは、条件「\(A\)組のクラスで体育会系の部に属していた男女のペア(これは、単一でも複数であってもよいとする)」を満たすもののみ受け付けることでき、そうでない場合には、受け付けず処理を行わないものとする。プログラムが受け付けた場合、同一の体育会系の部に属している場合には\(True\)を、異なる体育会系の部に属している場合には\(False\)を返すものとする。そして、プログラムが受け付けてくれるものを\(A \times B\)の候補ということにしよう。
例えば、\(A\)組テニス部所属\(B1\)君と\(A\)組水泳部所属\(G1\)さんの\(P1=(B1,G1)\)をプログラムに入力したとしよう。二人とも\(A\)組に属し、体育会系の部に属するので、プログラムは受け付けてくれ、\(False\)が返ってくる。従って、\(p1\)は\(A \times B\)の候補である。
次の例はどうであろうか。\(B\)組所属の男子\(b2\)と\(A\)組テニス部所属の女子\(G2\)の対\(P2=(B2,G2)\)をプログラムに入力したとしよう。男子が\(A\)組でないので、このプログラムはこの入力を受け付けない。このため、\(P2\)は候補とならない。
それでは、\(A\)組卓球部所属の男子\(B3\)と\(A\)組ダンス部所属の女子\(G3\)の対\(P3=(B3,G3)\)をプログラムに入力したとしよう。この入力は受け付けられる。このため、\(P3\)は候補となる。
このようなことを繰り返し行ったとすると、いくつもの候補が上がるであろう。その中で、不足することなく条件に合う対となっているのはどれであろうか。\(A\)組体育会系の部に所属する男子\(Bas\)と\(A\)組体育会系の部に所属する女子\(Gas\)の対であることは容易に分かる。
これを図で表してみよう。\(P1\)と\(P3\)と\(Bas \times Gas\)が候補であり、\(A \times B = Bas \times Gas\)が条件を満たす最大の集合であることが分かったので、次の可換図式を得る。図において\(incl\)は包含関数である。
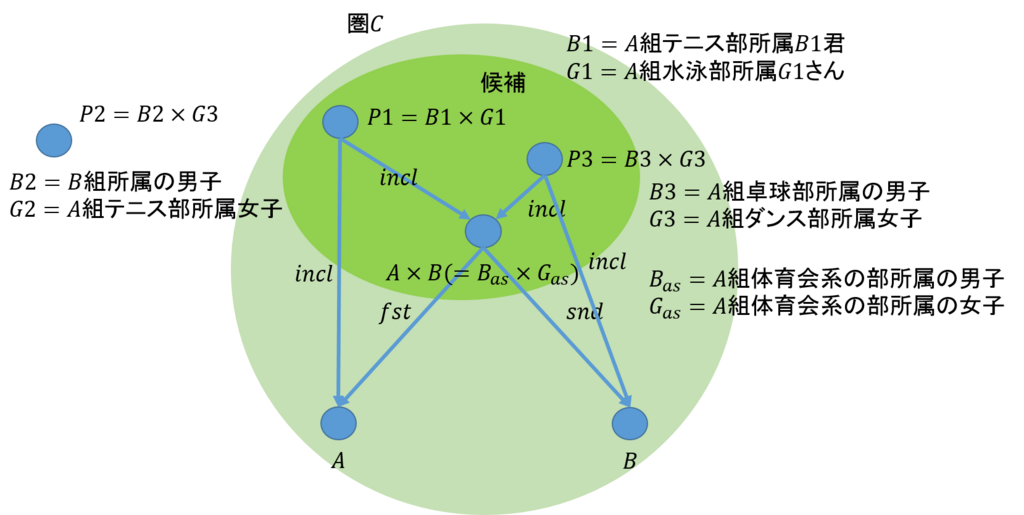
この例で、\(A \times B \)の候補となるのは、\(Bas \times Gas\)の部分集合であることが分かる。
例題2
先の例は離散系であったので、今度は連続した空間での例を挙げることにしよう。ある地域\(R\)の標高と年間平均気温の関係を表すことを考えよう。今、標高の方は赤色で表すことにし、高いほど濃くなるようにした。また、気温の方は黄色で表すことにし、低いほど濃くなるようにした。これらの色は絵の具で混ぜることにした。従って、標高が高く気温が低いほど、橙色は濃くなり、反対の場合には薄くなる。
標高を赤色で表した地域\(R\)の地図を\(A\)とし、年間平均気温を黄色で表した\(R\)の地図を\(B\)とした時、このような地図をその一部でも作成できるようなものを探すこととしよう。前の例に習って、これを\(A \times B\)の候補と呼ぶことにしよう。
\(R\)内のある地点\(R1\)での標高を\(P1_h\)とし、その地点での年間平均気温を\( R1_t\)とした時、\(R1=(R1_h, R1_t\)は、求められている地図の一部を描くことができるので、候補となる。
\(R\)の隣の地域\(R2\)での標高を\(R2_h\)とし、そこの年間平均気温を\( R2_t \)とした時、\(R2=(R2_h, R2_t)\)は、求められている地図の範囲外であるので、候補とはならない。
\(R\)に含まれる小さな地域\(R3\)での標高を\(R3_h\)とし、そこの年間平均気温を\( R3_t \)とした時、\(R3=(R3_h, R3_t)\)は、求められている地図の一部を描くことができるので、候補となる。
\(R\)に含まれる小さな地域\(R4\)での標高を\(R4_h\)とし、\(R\)内の別の地域\(R4’\)の年間平均気温を\( R4’_t \)とした時、\(R4=(R4_h, R4’_t)\)は、求められている地図の一部を描くことができないので、候補とならない。
\(R\)に含まれる小さな地域\(R5\)での標高を\(R5_h\)とし、\(R5\)の年間日照時間を\( R5_s \)とした時、\(R5=(R5_h, R5_s\)は、求められている地図の一部を描くことができないので、候補とならない。
これらの関係を可換図式で示したのが、下図である。
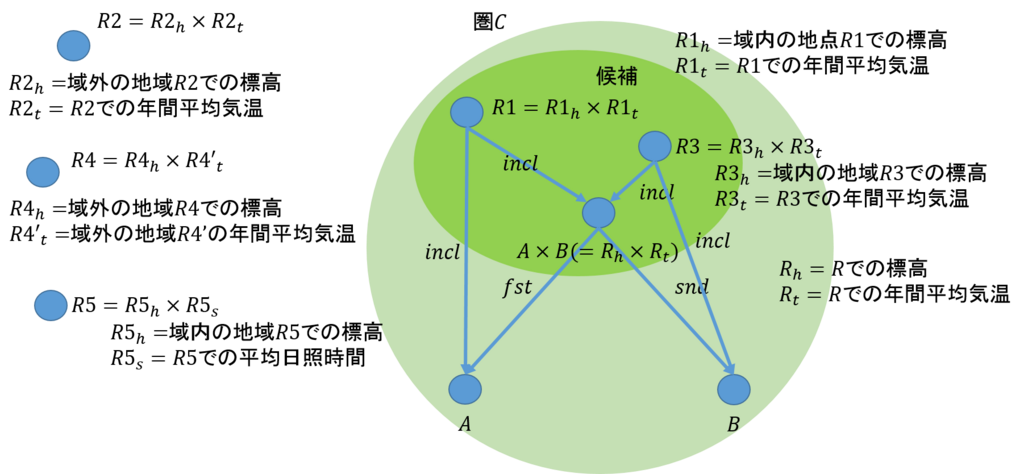
この例でも、\(A \times B \)の候補となるのは、\(R_h \times R_t\)の部分集合であることが分かる。
1.2 積の定義
圏では積は次のように定義される。
\(\mathcal{C}\)を適当な対象\(A,B\)を有する圏とする。\(A\)と\(B\)の積は、\(A \times B\)と書かれる\(\mathcal{C}\)の対象と二つの射\(fst : A \times B \rightarrow A \)および\(snd : A \times B \rightarrow B \)との組で、以下の普遍性を満たすものをいう。
積の普遍性
任意の対象\(X\)(これは例題1,2では候補と呼んでいたもの)および射の対\(p:X \rightarrow A\)および\(q:X \rightarrow B\)が与えられた時、一意的な射\(m : X \rightarrow A \times B\)が存在して、下図
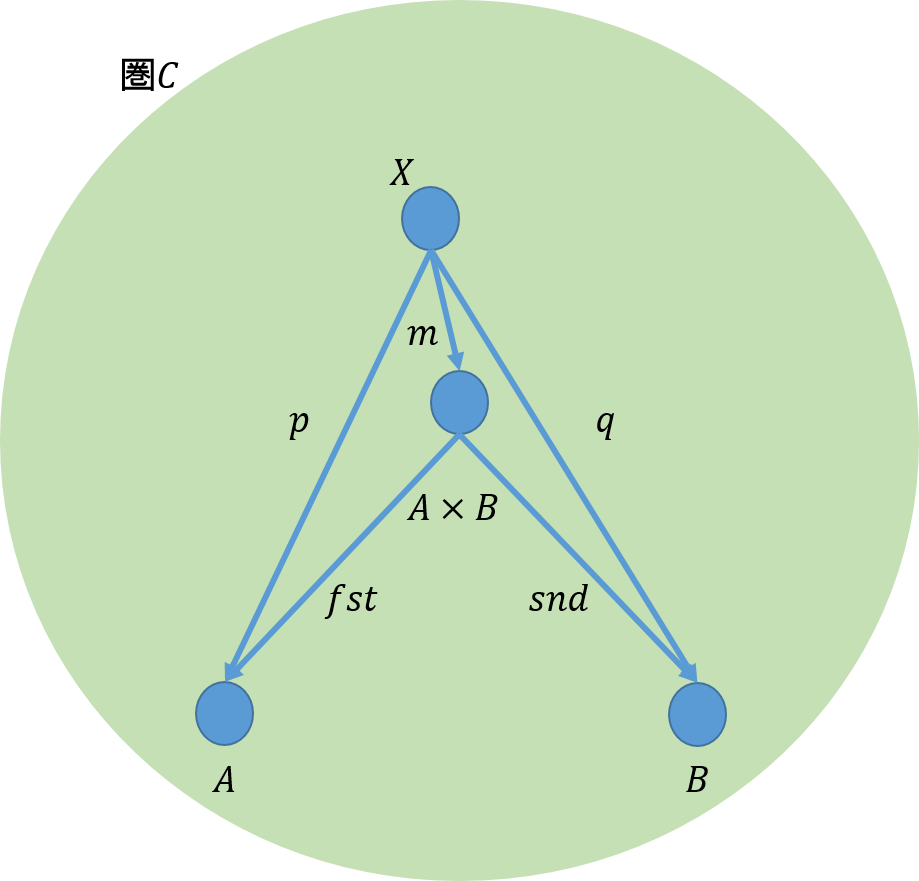
を可換にする。
上の定義から、この圏では、\(A\)と\(B\)への射を有するどのような対象を持ってきたとしても、積の普遍性が満たされる。即ち、\(A\)と\(B\)への射\(p'\)と\(q'\)を有する任意の対象\(X’\)を持ってきたとしても下図のように可換性が成り立ち、一意的な射\(m’ : X’ \rightarrow A \times B\)が存在する。
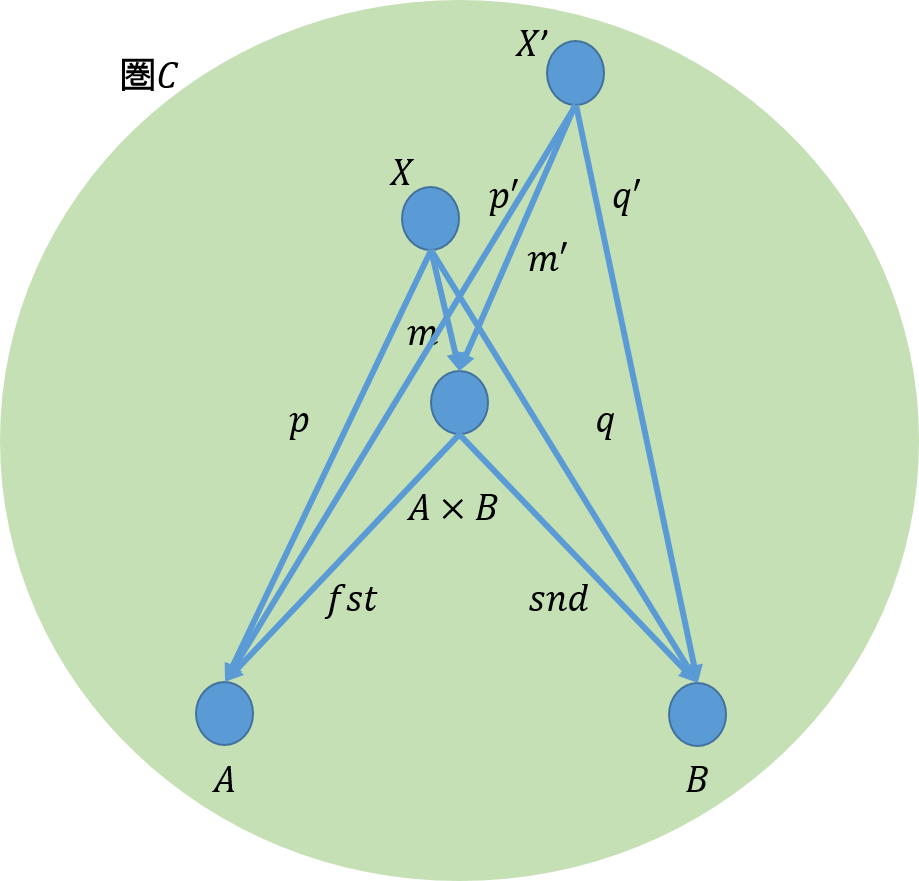
このことから、このような全ての対象(例題1,2で候補と言っていたもの)の中で、\(A \times B\)が\(A\)および\(B\)への最も優れた射(射の合成として表されないという意味で優れたということにする)を与えることから、極限ともいわれる(ただし、極限はのちの説明ではもっと一般的に使う。候補の中で、どれよりも優れた射を有するものと理解して欲しい)。
理解を深めるためには、次の問題を解くことを勧める。