モノイドを攻略する

３．　モノイドとコモノイド

今回はモノイド(monoid)と、そして、その双対であるコモノイド(comonoid)を説明しよう。モノイドという用語を使うと難解だと感じる読者も多いことだろうが、小学校以来学んできた足し算や掛け算などの多くの二項演算に関するものだ。モノイドという概念を、最初に理論的に学ぶのはおそらく群論だろう。

今回は、群論から入って、圏論の世界へと進み、Haskellで実現するという長い旅に出ることにしよう。

３．１　群論における半群とモノイド

群論のスタートとなるのは半群だ。殆どの二項演算がこれに属す。その定義は次のようになっている。
[半群の定義]
集合\(S\)とその上の二項演算子\(\bullet : S \times S \rightarrow S\)が与えられたとき、

１）組\((S,\bullet)\)が結合律、すなわち\(S\)の任意の\(a,b,c\)に対して\((a \bullet b) \bullet c = a \bullet (b \bullet c) \)が成り立つ

ならば、これを半群という。

引き算と割り算は結合律が成り立たないので半群とはならないが、足し算と掛け算は結合律が成り立つので半群となる。

半群の中で、単位元を有し、単位律が成り立つものをモノイドという。即ち、
[モノイドの定義]
集合\(S\)とその上の二項演算子\(\bullet : S \times S \rightarrow S\)が与えられたとき、

１）組\((S,\bullet)\)が結合律、すなわち\(S\)の任意の\(a,b,c\)に対して\((a \bullet b) \bullet c = a \bullet (b \bullet c) \)が成り立ち

２）\(S\)に単位元\(i\)が存在し、単位律、すなわち、\(S\)の任意の\(a\)に対して\(i \bullet a = a = a \bullet i \)が成り立つ

ならば、これをモノイドという。

足し算での単位元は\(0\)、掛け算でのそれは\(1\)である。

３．２　モノイドを圏として構成する

群論でのモノイドを、圏論での圏として、構成することを考えてみよう。圏の主要な構成要素は対象と射である。高校までの数学で学んできた「集合と関数」の考え方に素直に従った場合、集合を対象に、関数を射にするのが自然のように思われるだろう。すなわち集合\(S\)を対象に、二項演算子\(\bullet : S \times S \rightarrow S\)を射にしてはと思うだろう。

このようにすると、困った問題が生じる。圏を構成するためには、射と射を結びつける合成を必要とする。射が二項演算子\(\bullet : S \times S \rightarrow S\)だとすると、合成は何にしたらよいのだろう。私も圏論を学び始めたときは、ここでおおいに悩んだ。

参考書に描かれているモノイドの概念図を長いこと見つめた後で、発想の転換が必要なのだと思えるようになった。群論での二項演算子\(\bullet\)は、結合律を求めている。これは射ではなく合成としての性質だ。そこで二項演算子を合成にしてみよう。このようにすると、合成させられるものは射ということになる。すなわち集合\(S\)は射となる。

次の難関は射のドメインとコドメインだ。二項演算子を乗算と考えると、乗算が合成で、その被乗数と乗数が射ということになる。射は矢(arrow)と書かれることも多いが、矢はどこから来て、どこに行くのだろう。数学的な言葉で言うと、ドメインとコドメインをどのように定めたらよいのだろう。

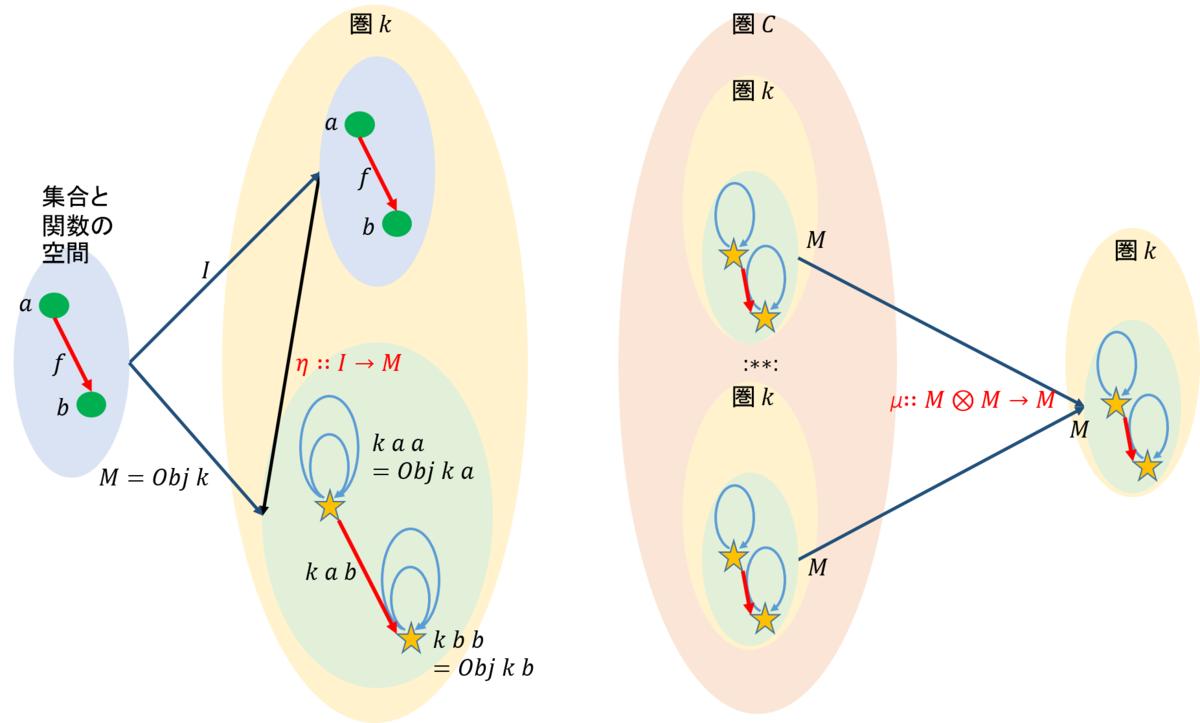
矢は連続して何本も打たれることがある。数学的な言葉でいうと合成だ。これに似たような現象は、行ったきりの矢ではなく、手元に戻ってくるブーメランだ。そこで、ブーメランの手元をドメイン、コドメインとすることにしよう。手元はただ一つなので、これを★ということにしよう。そしてドメインとコドメインは対象となる。対象はこれだけということにしよう。図で表すと下図のようになる。

図１：モノイドの概念図

このような考え方を元にして、モノイドを圏として構成しよう。

項目	構成要素
対象の集まり	★
射の集まり	\( S =\{a,b,c,…\} : ★ \rightarrow ★ \)
ドメインとコドメイン	★
恒等射	\(i \in S \)
合成	\(\bullet\)
結合律	\( (f \bullet g) \bullet h = f \bullet (g \bullet h) \ where f,g,h \in S \)
単位律	\( i \bullet f = f = f \bullet i \ where f \in S\)

具体的な例を示そう。正整数の乗算は次のように構成することができる。

項目	構成要素
対象の集まり	★
射の集まり	\( S =\{1,2,3,…\}: ★ \rightarrow ★ \)
ドメインとコドメイン	★
恒等射	\(1\)
合成	\(\times\)
結合律	\( (f \bullet g) \bullet h = f \bullet (g \bullet h) \ where f,g,h \in S \)
単位律	\( i \bullet f = f = f \bullet i \ where f \in S\)

圏は条件を満たすように構成要素を定義すればよいので、モノイドを圏として表す方法は、この外にも考えることができる。しかし数学者は簡潔で優雅な表現を求めるので、現在のところこれが最も的確な表現だと彼らは思っている。

３．３　Haskellでのモノイドの定義

それではHaskellで、モノイドがどのように実装されているかを見てみよう。Hasekllでは\(Semigroup\)というクラスを用意し、その下位クラスで\(Monoid\)を定義している。
\(Semigroup\)の定義は簡単で、二項演算子\( (< >) \)を定義している。

class Semigroup m where
  (<>) :: m -> m -> m

また結合律については、このクラスのインスタンスはこれを満足しなければならないという約束になっている。

そしてモノイドは次のように、単位元を\(mempty\)とし、二項演算子を\(mappend\)で置き換えている。

class Semigroup m => Monoid m where
  mempty :: m
  mappend :: m -> m -> m
  mappend = (<>)

但し次の条件を満たさないといけない。

x <> mempty = x
mempty <> x = x
(x <> y) <> z = x <> (y <> z)

このようにHaskellでの定義は、群論での定義を踏襲していることが分かる。そして圏論の圏としては定義されていないことも分かる。

３．４　モノイドの例

モノイドの例を上げよう。よく使うのはリストだろう。これは次のように定義できる。

instance Semigroup [a] where
  (<>) = (++)
instance Monoid [a] where
  mempty = []

なお、要求されている単位律や結合律が満たされていることは明らかである。

馴染みのあるところで、掛け算の例も挙げておこう。被乗数と乗数は\(Product\)というデータ型で定義されているとしよう。

newtype Product n = Product n
instance Num n => Semigroup (Product n) where
  Product x <> Product y = Product (x * y)
instance Num n => Monoid (Product n) where
  mempty = Product 1

同じように足し算は次のようになる。

newtype Sum n = Sum n
instance Num n => Semigroup (Sum n) where
  Sum x <> Sum y = Sum (x + y)
instance Num n => Monoid (Sum n) where
  mempty = Sum 0

もう少し、複雑な例を挙げてみよう。デカルト積だ、これは二つの対象の積だ。例えばトランプは種類\(S=\{♡,♠,♦.♣\}\)と数字\(T=\{1,2,,,,9,J,Q,K\}\)の対\(S \times T\)、例えば\((♠,9)\)、で表されるが、これはデカルト積の一例だ。Haskellでは次のように定義できる。

instance Semigroup () where
  _ <> _ = ()
instance Monoid () where
  mempty = ()
instance (Semigroup a, Semigroup b) => Semigroup (a, b) where
  (a, b) <> (a’,b’) = (a <> a’, b <> b’)
instance (Monoid a, Monoid b) => Monoid (a, b) where
  mempty = (mempty, mempty)

ここで、\(((),a)\)と\(a\)とが同型であることに注意しておく必要がある。圏論的に表現すれば、\(((),A) \cong A\)である。
少し利用してみよう。ここでは\(Monoid\)のクラスで用意されているものを利用した。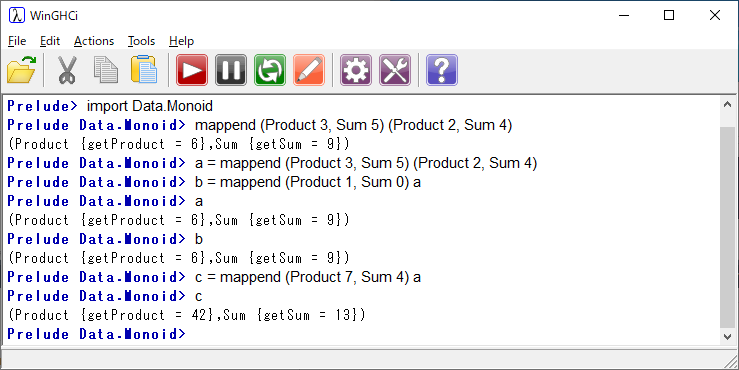

図２：Haskellでの実行例

これまでにあげた例は二つの項の積だが、これらを最も抽象化したものがテンソル積である。

３．５　モノイド対象

この記事の最初の方で、群論での半群とモノイドを説明し、そしてそれを圏として次のように構成した。

項目	構成要素
対象の集まり	★
射の集まり	\( S =\{a,b,c,…\} : ★ \rightarrow ★ \)
ドメインとコドメイン	★
恒等射	\(i \in S \)
合成	\(\bullet\)
結合律	\( (f \bullet g) \bullet h = f \bullet (g \bullet h) \ where f,g,h \in S \)
単位律	\( i \bullet f = f = f \bullet i \ where f \in S\)

それでは、これをもう少し抽象化することにしよう。抽象化の一つは関手を導入することだ。関手は圏から圏への関数なので、圏を対象とし、関手を射とすることができる。いま、圏\(\mathcal{C}\)から同じ圏\(\mathcal{C}\)への関手\(M\)を考えてみよう。また関手と関手の合成を\( \otimes \)とすると、次の左側の図が得られる。そして圏\(\mathcal{C}\)を★で表し、これを一か所にまとめると右の図が得られる。これは先に述べたモノイドと同じようには見えるはずだ。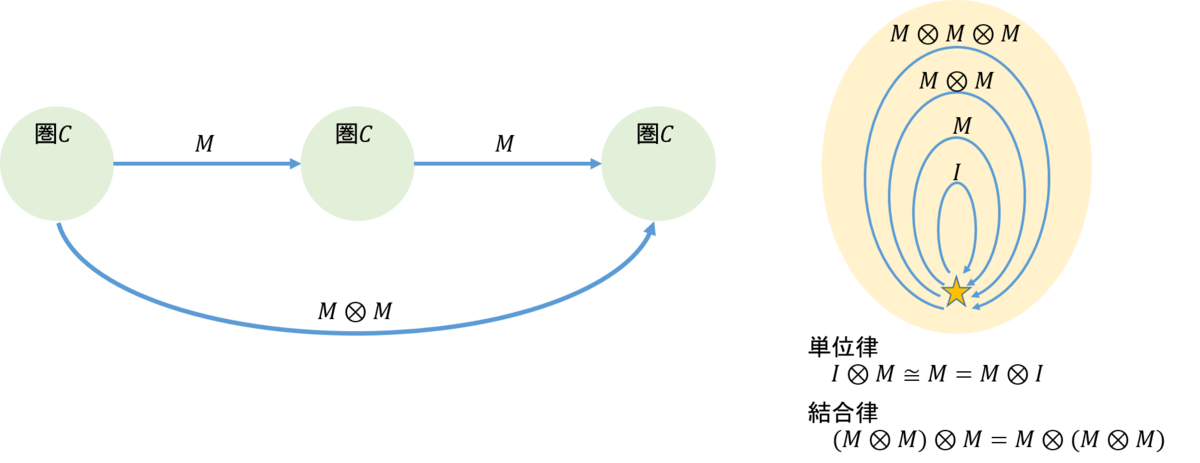

図３：一つの関手\(M\)を射としてモノイドを構成

これを圏として構成したのが次の表の右側だ。

項目	群論からのモノイド	モノイド対象\(M\)
対象の集まり	★	\(\mathcal{C}\)
射の集まり	\( a,b,c,…\in S\)	\( M : \mathcal{C} \rightarrow \mathcal{C}\)
ドメイン	★	\(\mathcal{C}\)
コドメイン	★	\(\mathcal{C}\)
恒等射	\( i \in S \)	\(I : \mathcal{C} \rightarrow \mathcal{C}\)
合成	\(\bullet\)	\( \otimes \)
単位律	\(i \bullet a = a = a \bullet i\)	\(λ : I \otimes M \cong M \\ ρ : M \cong M \otimes I\)
結合律	\((a \bullet b) \bullet c =a \bullet (b \bullet c) \)	\( α : (M \otimes M) \otimes M \cong M \otimes (M \otimes M)\)

すなわち圏\(\mathcal{C}\)を対象とし、関手\(M\)を射とし、そして自身への関手\(I\)を恒等射とし、関手と関手の合成\(\otimes\)をモノイドでの合成としたものだ。もちろん単位律
\begin{eqnarray}
λ : I \otimes M \cong M \\
ρ : M \cong M \otimes I
\end{eqnarray}
と結合律
\begin{eqnarray}
α : (M \otimes M) \otimes M \cong M \otimes (M \otimes M)
\end{eqnarray}
は満たさなければならない。なお上記で\( \cong \)は自然同型である。自然同型について簡単にふれておこう。ある空間\(A\)からある空間\( B\)への射\(f\)が逆写像を有するとき、射\(f\)を同型射あるいは単に同型という。空間を圏とし、写像を関手としたときに、関手にたいして同様なことが成り立つときに、自然同型という。

もう少し厳密に説明すると、圏\(\mathcal{C}\)から圏\(\mathcal{D}\)へ関手\(F,G\)が存在し、\(F\)から\(G\)への射\(η\)(これは自然変換と呼ばれる)が存在したとする。このとき、\(\mathcal{C}\)の任意の対象\(x\)に対して\(η_x\)が圏\(\mathcal{D}\)の同型射となっているとき、自然同型という。図で示すと下図のとおりである。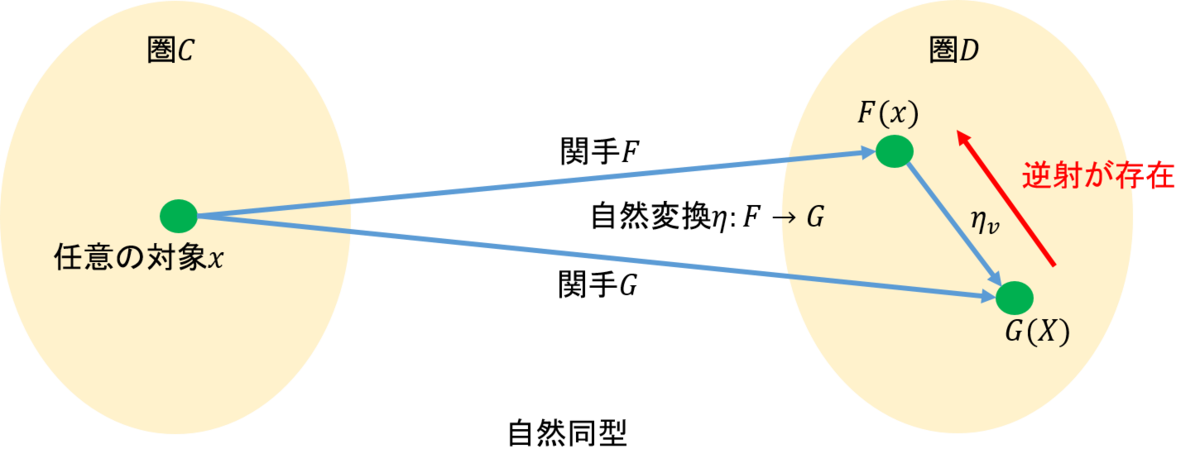

図４：自然同型は成分ごとに同型射となることを言う

さて今導入したモノイドの構造では、モノイドが有する性質、すなわち二項演算子が見えにくい。そこで射\(M,I\)を対象にし、モノイドの構造が現れるようにしよう。二項演算子を一般化するとテンソル積となるが、ここではこれを表すために\(\otimes\)を用いよう。そしてテンソル積が圏の構成の中で表れるようにしよう。すなわち、テンソル積\(μ: M \otimes M \rightarrow M\)を射と考えることにしよう。

さらにもう一つはモノイドという対象を作り出してくれる射だ。これを\(η:I \rightarrow M\)としよう。ビッグバンに似たような性質を持つ。ビッグバンによって宇宙が生じたように、\(η\)は対象\(M\)を生み出す。

なお\(μ,η\)は関手から関手への射なので、自然変換である。

最後に単位律と結合律が成り立つようにしなければならないが、これは同じである。。

項目	モノイド対象\(M\)	抽象化(射を対象に)
対象の集まり	\(\mathcal{C}\)	\( M, I \)
射の集まり	\( M : \mathcal{C} \rightarrow \mathcal{C}\)	\( μ : M \otimes M \rightarrow M \\ η:I \rightarrow M \)
ドメイン	\(\mathcal{C}\)	\((M,M),I\)
コドメイン	\(\mathcal{C}\)	\(M\)
恒等射	\(I : \mathcal{C} \rightarrow \mathcal{C}\)	\(I_M : M \rightarrow M \)
合成	\( \otimes \)	\(\otimes\)
単位律	\(λ : I \otimes M \cong M \\ ρ : M \cong M \otimes I\)	\(λ : I \otimes M \cong M \\ ρ : M \cong M \otimes I\)
結合律	\( α : (M \otimes M) \otimes M \\ \cong M \otimes (M \otimes M)\)	\( α : (M \otimes M) \otimes M \\ \cong M \otimes (M \otimes M)\)

このようにしてできたのは、一般に、モノイド対象と呼ばれる。これまでの話をまとめて、モノイド対象を定義してみよう。

[モノイド対象の定義]

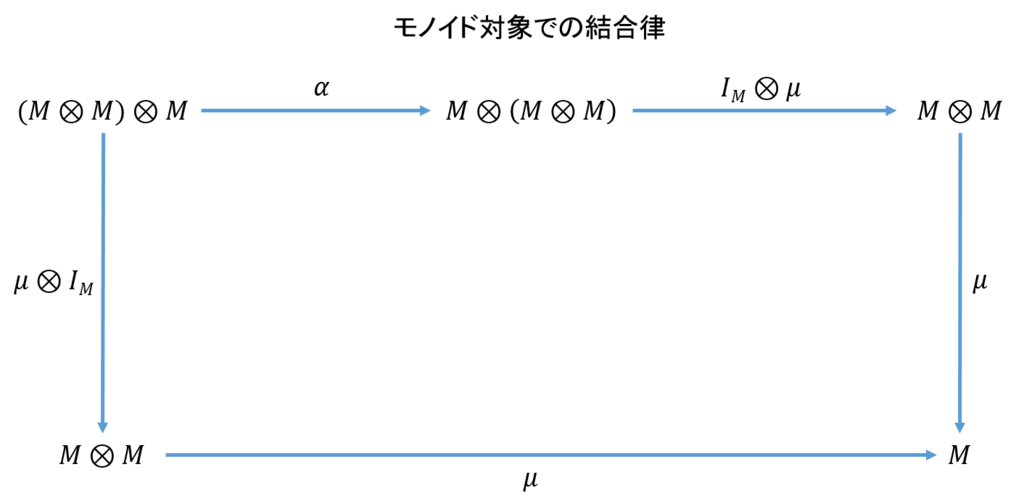
モノイド対象( \( M,μ,η\))とはモノイド圏(\( \mathcal{C}, \otimes, I, α, λ, ρ \))が与えられた時、\(\mathcal{C}\)の対象\(M\)および二つの射(\(μ : M \otimes M \rightarrow M, η: I \rightarrow M \))を有し、下記の単位子図式と五角形図式を満たすものである。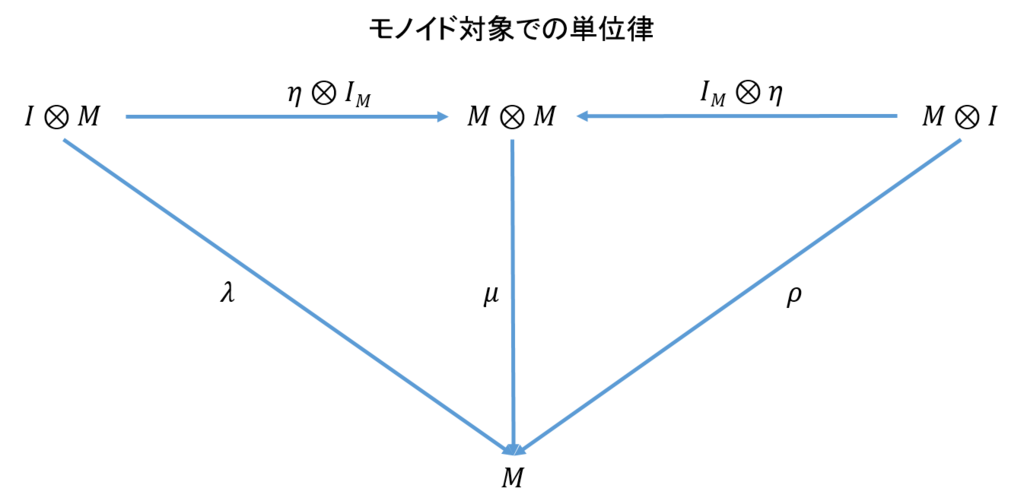

図５：モノイド対象での単位子図式

図６：モノイド対象での五角形図式

３．６　モノイド圏

モノイド圏は一つまたは複数のモノイド対象をその対象にしたもので次のように定義される。

[モノイド圏の定義]

モノイド圏(\( \mathcal{C}, \otimes, I, α, λ, ρ \))とは、圏 \(\mathcal{C} \)が次の条件を備えているときである。
1) テンソル積と呼ばれる双関手\(\otimes : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C} \)
2) モノイド単位(あるいは単位対象)\(I\)
3) 結合律：\(α_{A,B,C}: (A \otimes B) \otimes C \cong A \otimes (B \otimes C)\)　(ただし、\(α\)は自然同型)
4) 右単位律：\(λ_A : I \otimes A \cong A \), 左単位律：\(ρ_A : A \otimes I \cong A \)　(ただし、\(λ, ρ\)は自然同型)
モノイド圏を概念図で表すと以下のようになる。

図７：モノイド圏の概念図

モノイド圏とモノイド対象との関係を概念的に表すと下図になる(ここでのモノイド圏は一つのモノイド対象を持つものとする)。

図８：モノイド圏とモノイド対象の関係

またモノイド圏の単位律と結合律に関する可換図を下図に示す。

図９：モノイド圏での単位律を表す可換図

図１０：モノイド圏での結合律を表す可換図

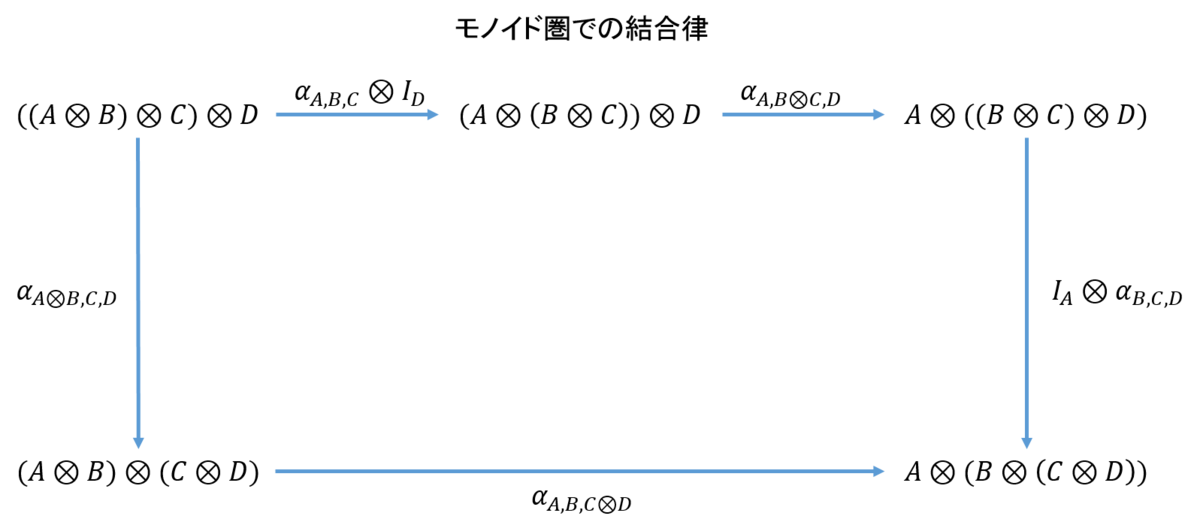
３．７　コモノイド

モナイド圏とモナイド対象の矢印を逆にするとこれらと双対の関係にあるコモノイド圏とコモノイド対象を得ることができる。そこで、ここではコモナイド対象について少し詳しく説明しよう。

モノイド対象( \( M,μ,η\))は、モノイド圏(\( \mathcal{C}, \otimes, I, α, λ, ρ \))が与えられた時、\(\mathcal{C}\)の対象\(M\)および二つの射(\(μ : M \otimes M \rightarrow M, η: I \rightarrow M \))を有し、下記の単位子図式と五角形図式を満たすものであった。この定義の中で重要なのは、モノイド対象を定義している二つの射(\(μ : M \otimes M \rightarrow M, η: I \rightarrow M \))だ。

そこで、ここでは、これら二つについて考えてみることにしよう。矢印の方向を反対にすると、
\begin{eqnarray}
δ : M \rightarrow M \otimes M \\
ε: M \rightarrow I
\end{eqnarray}

となる。\(δ\)は、対象のコピーを取って対にしているだけなので、面白いことをしてはいない。このようなわけで、Haskellにはコモナドは実装されていないが、実現することは次のように可能である。

class Comonoid m where
  split :: m -> (m,m)
  destroy :: m -> ()

instance Comonoid a where
  split a = (a,a)
  destroy a = ()

モナドが自己関手の(小さい圏の)圏で記述されたモノイドと同じであったが、同様なことがコモナドとコモノイドについても言える。コモノイドは面白くもなんともないのに、これから生じるコモナドが前の記事で書いたようにとても実用的な性質を持っている。このギャップがコモノイドとモノイドの関係を魅力的にさせてくれる。

３．８　Haskellでの実装

モノイドとコモノイドの理解を深めるために、Haskellでどのように実現されているかを見ていくことにしよう。本格的ではないが、実験的なものが、ライブラリー"data-category"として用意されている。これをダウンロードしよう。解凍したフォルダーの直下にDataと呼ばれるフォルダーがある。ここが、このライブラリーを用いるときの先頭になるフォルダーだ。

それではこのライブラリーを使ってみよう。Dataの直下に、Category.hsと呼ばれるHaskellのソースプログラムがあるので、これをHaskellのプラットフォームであるWinGHCiにドラッグ&ドロップする。ソースプログラムがロードされ、このプログラムが実行できるようになる。

しかし我々が実行したいのは、フォルダーCategoryの直下にあるMonoidal.hsだ。Category.hsをロードした時点でのディレクトリーはCategoryになっているので、一つ上のディレクトリーDataに移したあと、Monoidal.hsをロードする。このときドラッグ&ドロップを用いず、キーボードより

:load "Data/Category/Monoidal.hs"

と打ち込む必要がある。さもないと、ロードに先立ってディレクトリーがData/Categoryに移動してしまう。

それでは、環境が整ったので、プログラムの中身を見ることにしよう。

図１１：Monoidalのパッケージを利用できるように関連するファイルをロードする

１）圏を定義する

ライブラリーを作成した作者は、ソースコードをアップロードしているだけで、その考え方を説明していない。このためプログラムを説明するときには、作者の意図を読み解いていくことが必要だ。もしかすると作者の意図とは異なるかもしれないが、ライブラリーのソースコードを読んでいくことにしよう。なお、このライブラリーは一から作り上げているので、とても基本的なところからスタートする。

ライブラリーは圏を定義するための\(Category\)と呼ばれるクラスを用意している。しかし理解しやすくするために、そのもとになっているだろうと思われる考え方を最初に説明しておこう。

集合と関数は馴染みのある言葉だ。集合\(A\)と\(B\)があり、\(A\)のそれぞれの要素に対して\(B\)のある要素を割当てる関数\(f\)があるというのが出発点になっている。さらに集合\(C\)があり、\(B\)から\(C\)へ写像する関数\(g\)がある。このとき、\(f\)と\(g\)を合成した関数は、\(A\)から\(C\)への写像となる。これを\(h\)で表すと、\(h (x) = g \circ f (x)\)となる。

このような集合と関数の概念を、圏論の世界で、なるだけ一般的に表そうとしたのが、アロー(arrow)と呼ばれる概念だ。そこではすべてをアローで表す。アローは\(k \ a \ b\)で表され、これは射\(k\)が\(a\)から\(b\)へと向かうと考えるとよい。

先の集合と関数で説明した関数\(f\)は\(k \ A \ B\)となり、集合\(A\)は恒等射\(k \ A \ B\)となる。また、関数の合成\(g \circ f\)は\(k \ B \ C \ . \ k \ A \ B\)となり、準同型写像となる。

上で説明した集合を任意のものについて論じている場合には、Haskellでは型変数を用い、その場合には小文字を用いる。例えば\(f\)は\(k \ a \ b\)のようになる。

これを図で表すと以下のようになる。これからも分かるように、集合と関数の空間からアローだけで構成された世界へと関手\(arr\)で写像して圏を構成している。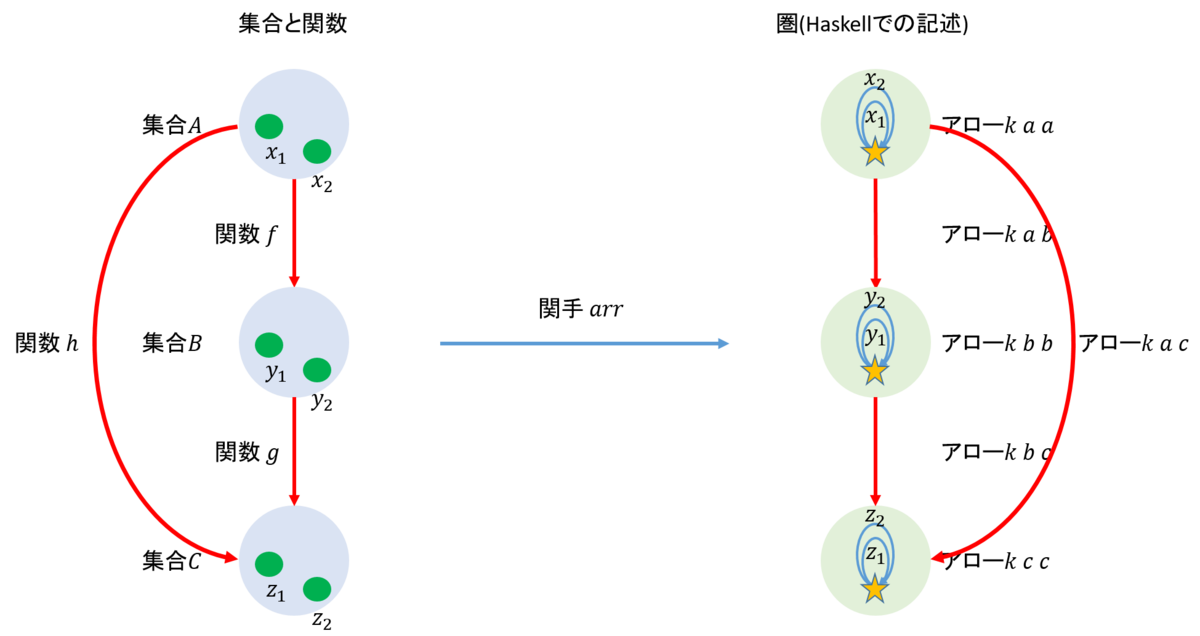

図１２：アロー\(k \ a \ b \)は\(a\)から\(b\)へと向かう射\(k\)であるが、関手\(arr\)によって集合と関数の世界からアローだけで構成された世界へと移動することができる。

それではライブラリーの説明に移ろう。そこではオリジナルが集合であったアローを明確にするため、\(Obj \ k\)というデータ型を用意している。

type Obj k a = k a a

そして、集合と関数の時の関数のソースとターゲットを明確にするために、それらのメソッドを用意して、次のように\(Category\)の定義をしている。

class Category k where 
  src :: k a b -> Obj k a 
  tgt :: k a b -> Obj k b 
  (.) :: k b c -> k a b -> k a c 

圏としての構造をまとめると次のようになる。これからも分かるように、極めて単純な構造であることが分かる。

圏	\(k\)
対象の集まり	★
射の集まり	\(k \ a \ b \)
ドメインとコドメイン	★
恒等射	\(id_a :: k \ a \ a \)
合成	(.)
結合律	\( (k \ c \ d . k \ b \ c) . k \ a \ b = k \ c \ d . ( k \ b \ c . k \ a \ b) \)
単位律	\(id_b . k \ a \ b = k \ a \ b = k \ a \ b . id_a \)

このクラスにはインスタンスが一つだけ用意されている。それは\(k\)を関数\( (->)\)としたものだ。関手\(arr\)で一度持ち上げておいて、元に戻すようで変な感じになるが、集合の部分が射で表されているので、元の集合と関数の世界とは違うことに注意しよう。

instance Category (->) where 
  src _ = \x -> x 
  tgt _ = \x -> x 
  g . f  = \x -> g (f x)  

圏の構造を示すと次のようになる。

圏	\(->\)
対象の集まり	★
射の集まり	\(f,g,h,… \)
ドメインとコドメイン	★
恒等射	\(id\)
合成	(.)
結合律	\( (f . g) . h = f . ( g . h) \)
単位律	\(id . f = f = f . id \)

実行例を示してみよう。但し、”Data.Category”には関数が実装されていないので、”Control.Arrow”のライブラリーをインポートして使った。以下の実行例で、\(x -> x \)は入力、\(y -> y \)は出力を意味し、集合での\(A\)と\(B\)に相当する。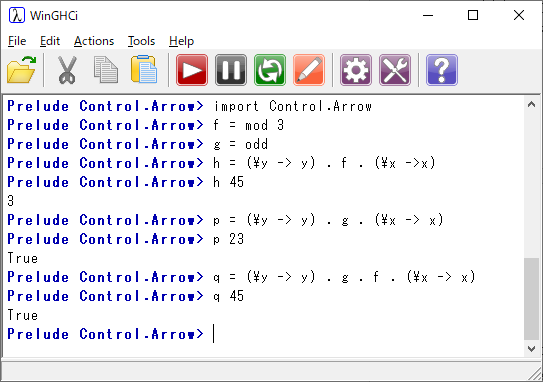

図１３：アローを用いた世界での実行例

２）終対象を用意する

この記事では示さなかったが、モノイドは終対象を持つ。終対象に対するクラス\(HasTerminalObject\)は次のように定義されている。

class Category k => HasTerminalObject k where
  type TerminalObject k :: * 
  terminalObject :: Obj k (TerminalObject k) 
  terminate :: Obj k a -> k a (TerminalObject k) 

図で示すと次のようである。なお図では集合と関数の関係が、圏として構成された後にも反映ざれるように、元々は集合であった部分を薄緑色で表した。ライブラリーの作成者も\(Obj\)という言葉を用いたのはそのためだろう。しかし、圏の構成から見るとこれらは射であることに注意しておこう。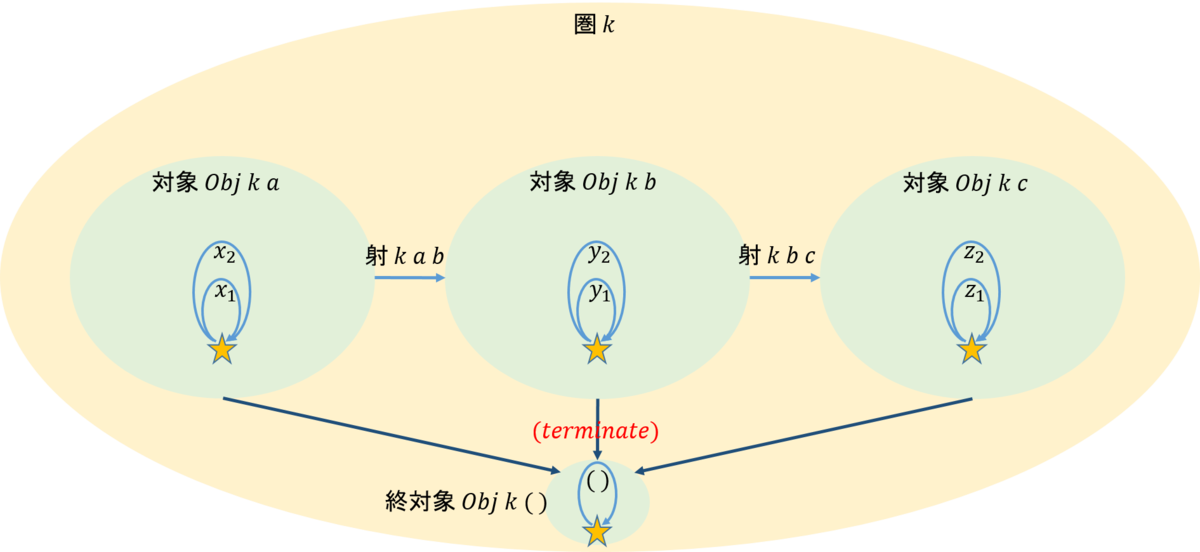

図１４：終対象を定義する。

インスタンス\(->\)は次のように定義されている。

instance HasTerminalObject (->) where 
  type TerminalObject (->) = () 
  terminalObject = \x -> x 
  terminate _ _ = () 

３）バイナリー積を用意する

次はいよいよ二項演算だ。もう一度、アローの話に移そう。アローを構成するものはすべてが射だ。そしてアローはつなぎ合わせることが可能だ。まるでシステムを構成する部品のようだ。しかも部品の種類が一種だけ、全てがアローというのも魅力的だ。部品のつなぎ方には、直列と並列がある。

直列接続は合成だ。並列接続は二項演算だ。二項演算子の左右にはそれぞれ左の項と右の項があるが、これらの項は別々に計算した後で、二項演算を施せばよい。このため左右の項を別々に計算するという方法は、それぞれを別々に計算するという考え方へと導いてくれる。

そこでアローを並列に接続する方法を考えてみよう。二つのものを並列にすることを考えさえすれば、多数のものを並列に接続する手段を得ることができる。そこで二つを並列にする方法を考えてみよう。これは様々であるが、ここではライブラリーに実装されている並列接続を示そう。下図のようだ。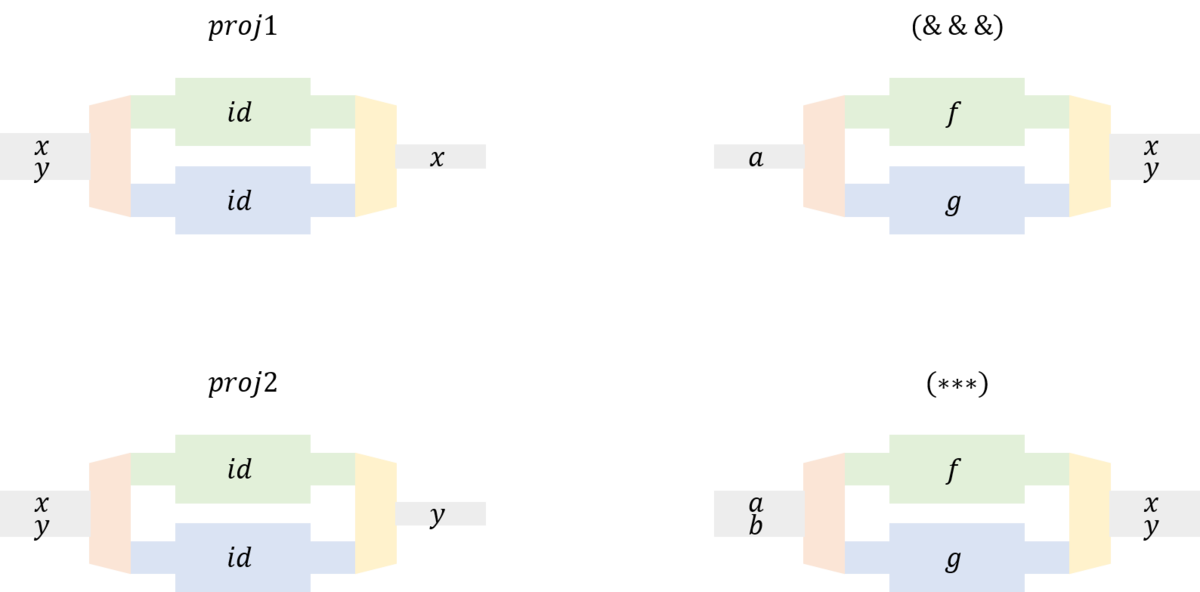

図１５：二つのアローを並列に接続する。

\(proj1,proj2\)は、二つの値を取り、その一方をとるものである。\( (\& \& \&) \)は一つの値に対して、二つの射\(f,g\)からの出力を得るというものだ。\( (\ast \ast \ast) \)は別々の値に対して、それぞれの射\(f,g\)からの出力を得るというものだ。

ところで並列処理にするためには、上図に示したように、複数の入力、複数の関数、複数の出力が必要になる。ライブラリーでは、この複数に対応するのが、バイナリー積(\(BinaryProduct\))だ。クラスの定義の中で\( BinaryProduct (k :: * -> * -> *) x y :: *\)と定義されている。また、インスタンス\( (->)\)に対しては\( BinaryProduct (->) x y = (x, y) \)と定義されている。

ライブラリーではクラスは次のように定義されている。

class Category k => HasBinaryProducts k where 
  type BinaryProduct (k :: * -> * -> *) x y :: * 
  proj1 :: Obj k x -> Obj k y -> k (BinaryProduct k x y) x
  proj2 :: Obj k x -> Obj k y -> k (BinaryProduct k x y) y
  (&&&) :: k a x -> k a y -> k a (BinaryProduct k x y) 
  (***) :: k a x -> k b -> k (BinaryProduct k a b) (BinaryProduct k b1 b2) 
  l *** r = (l . proj1 (src l) (src r)) &&& (r . proj2 (src l) (src r)) 

そして\(->\)に対するインスタンスは次のようになっている。

instance HasBinaryProducts (->) where 
  type BinaryProduct (->) x y = (x, y) 
  proj1 _ _ = \(x, _) -> x 
  proj2 _ _ = \(_, y) -> y 
  f &&& g = \x -> (f x, g x) 
  f *** g = \(x, y) -> (f x, g y) 

４）圏同士のバイナリー積を用意する

モノイドを圏論として表すための準備がだいぶ整ってきた。モノイドを構成するのに必要とされる二つの圏の積を別の圏に関手で写像することを考えよう。

ここからの説明は下図を用いて行う。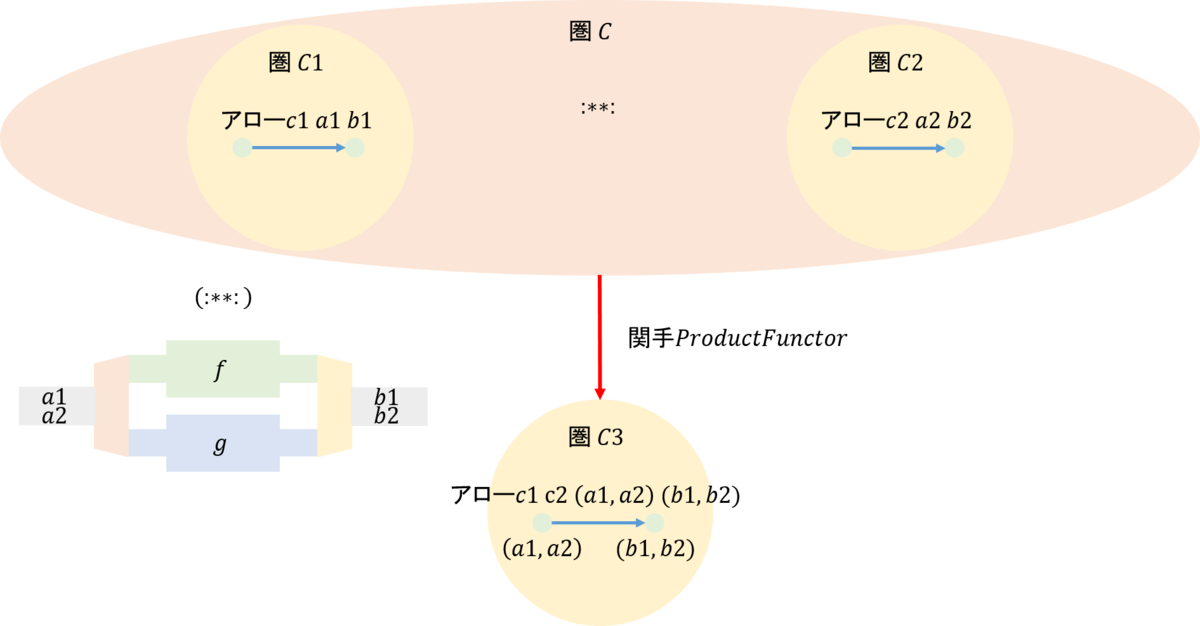

図１６：圏論の中でモノイドを定義する。

図に示したように、二つの圏\(\mathcal{C}1, \mathcal{C}2\)があるとし、それぞれから任意のアロー\( c1 \ a1 \ b1, c2 \ a2 \ b2 \)を取り出したとしよう。この積を\(:**:\)で表すこととしよう。この二項演算子は、アローの接続のところで示したように、それぞれのアローを並列に処理すると考えることができる。

さらに、圏\(\mathcal{C}1, \mathcal{C}2\)は圏\(\mathcal{C}\)の対象であるとしよう。また、圏\(\mathcal{C}\)からは双関手によって圏\(\mathcal{C}3\)に写像されるとしよう。すなわちアローの積\( (c1 \ a1, \ b1) :**: (c2 \ a2, \ b2) \)は双関手\(ProductFunctor\)によって、圏\(\mathcal{C}3\)のあるアロー\( c1 \ c2 \ (a1, a2 \ (b1,b2) \)に写像されるとする。

勘のいい読者は、これはモノイド圏だと、思っただろう。実際、モノイド圏の説明の中で用いた\(A,B,C=A \otimes B\)は\( c1 \ a1, \ b1), (c2 \ a2, \ b2), c1 \ c2 \ (a1, a2 \ (b1,b2) \)に対応し、テンソル積\(\otimes\)は\(:**:\)に対応する。また、\(\mathcal{C}1, \mathcal{C}2, \mathcal{C}3\)が同じとき、\(A,B,C\)は\(M\)となりモノイド対象となる。ライブラリーはこの関係を用いて実装されている。

それではライブラリーでどのように定義されているかを見ていくこととしよう。

data (:**:) :: (* -> * -> *) -> (* -> * -> *) -> * -> * -> * where
  (:**:) :: c1 a1 b1 -> c2 a2 b2 -> (:**:) c1 c2 (a1, a2) (b1, b2)

\(Category\)のインスタンスとして次のように定義されている。

instance (Category c1, Category c2) => Category (c1 :**: c2) where
  src (a1 :**: a2)            = src a1 :**: src a2
  tgt (a1 :**: a2)            = tgt a1 :**: tgt a2
  (a1 :**: a2) . (b1 :**: b2) = (a1 . b1) :**: (a2 . b2)

また、終対象に対しては次のように定義されている。

instance (HasTerminalObject c1, HasTerminalObject c2) => HasTerminalObject (c1 :**: c2) where 
  type TerminalObject (c1 :**: c2) = (TerminalObject c1, TerminalObject c2) 
  terminalObject = terminalObject :**: terminalObject 
  terminate (a1 :**: a2) = terminate a1 :**: terminate a2  

さらに、この圏がバイナリー積に対しては次のように定義されている。

instance (HasBinaryProducts c1, HasBinaryProducts c2) => HasBinaryProducts (c1 :**: c2) where 
  type BinaryProduct (c1 :**: c2) (x1, x2) (y1, y2) = (BinaryProduct c1 x1 y1, BinaryProduct c2 x2 y2) 
  proj1 (x1 :**: x2) (y1 :**: y2) = proj1 x1 y1 :**: proj1 x2 y2 
  proj2 (x1 :**: x2) (y1 :**: y2) = proj2 x1 y1 :**: proj2 x2 y2 
  (f1 :**: f2) &&& (g1 :**: g2) = (f1 &&& g1) :**: (f2 &&& g2) 
  (f1 :**: f2) *** (g1 :**: g2) = (f1 *** g1) :**: (f2 *** g2) 

５）テンソル積を用意する

それではいよいよテンソル積を定義することにしよう。

class (Category (Dom ftag), Category (Cod ftag)) => Functor ftag where 
  type Dom ftag :: * -> * -> * 
  type Cod ftag :: * -> * -> *
  type ftag :% a :: *
  (%) :: ftag -> Dom ftag a b -> Cod ftag (ftag :% a) (ftag :% b)

テンソル積のインスタンスを作ろう。そのために、二項演算に体操する双関手\(ProductFunctor\)を用意しよう。

data ProductFunctor (k :: * -> * -> *) = ProductFunctor 

それではこれを双関手としよう。

instance HasBinaryProducts k => Functor (ProductFunctor k) where 
  type Dom (ProductFunctor k) = k :**: k 
  type Cod (ProductFunctor k) = k 
  type ProductFunctor k :% (a, b) = BinaryProduct k a b 
  ProductFunctor % (a1 :**: a2) = a1 *** a2 

テンソル積のクラスは次のように定義されている。

class (Functor f, Dom f ~ (Cod f :**: Cod f)) => TensorProduct f where 
  type Unit f :: * 
  unitObject :: f -> Obj (Cod f) (Unit f) 
  leftUnitor :: Cod f ~ k => f -> Obj k a -> k (f :% (Unit f, a)) a 
  leftUnitorInv :: Cod f ~ k => f -> Obj k a -> k a (f :% (Unit f, a)) 
  rightUnitor :: Cod f ~ k => f -> Obj k a -> k (f :% (a, Unit f)) a 
  rightUnitorInv :: Cod f ~ k => f -> Obj k a -> k a (f :% (a, Unit f)) 
  associator :: Cod f ~ k => f -> Obj k a -> Obj k b -> Obj k c -> k (f :% (f :% (a, b), c)) (f :% (a, f :% (b, c))) 
  associatorInv :: Cod f ~ k => f -> Obj k a -> Obj k b -> Obj k c -> k (f :% (a, f :% (b, c))) (f :% (f :% (a, b), c)) 

これを用いてテンソル積のインスタンスは次のように定義されている。

instance (HasTerminalObject k, HasBinaryProducts k) => TensorProduct (ProductFunctor k) where 
  type Unit (ProductFunctor k) = TerminalObject k 
  unitObject _ = terminalObject 
  leftUnitor _ a = proj2 terminalObject a 
  leftUnitorInv _ a = terminate a &&& a 
  rightUnitor _ a = proj1 a terminalObject 
  rightUnitorInv _ a = a &&& terminate a 
  associator _ a b c = (proj1 a b . proj1 (a *** b) c) &&& (proj2 a b *** c) 
  associatorInv _ a b c = (a *** proj1 b c) &&& (proj2 b c . proj2 a (b *** c)) 

実行例を示そう。単位律、結合律が成り立っていることが分かる。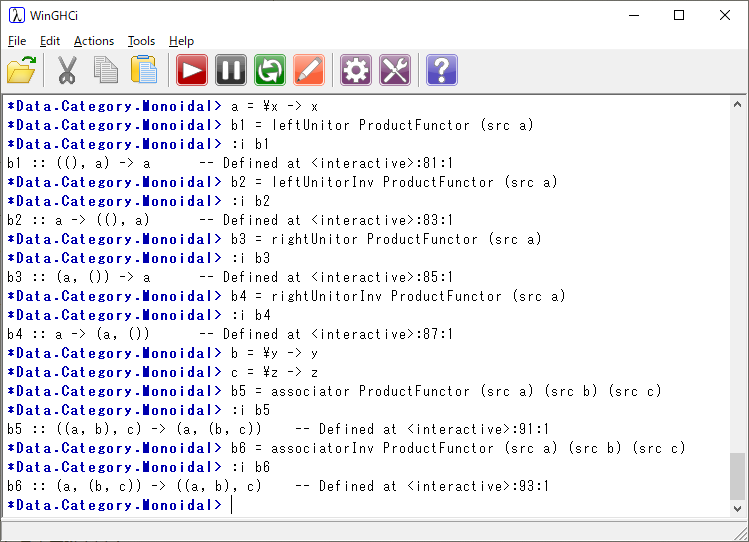

図１７：テンソル積のプログラムを実行する。

そして上記のインスタンスは、\(TensorProduct\)を\(\otimes\)とし、\( unitObject \ ( ) \)を\(I\)とすると、モノイド圏の定義と合致していることが分かる。また、下図に示すようにモノイド対象となることも分かる。

図１８：モノイド対象であることを示した概念図。