1.3 合成
射の合成は、圏を構成するための重要な道具の一つである。圏\(\mathcal{C}\)において、射\(f:A \rightarrow B, g:B \rightarrow C\)が存在したとき、\(f\)を計算し、その結果に対して\(g\)を計算することを、射の合成と言い、これを\( g \circ f\)と書く。いつも\( \circ \)を書くのは煩わしいので、今後はこれを省いて\( g f\)とする。これを\(h:A \rightarrow C\)を用いて、\( h=gf\)としたのが、図15である。
それではストリング・ダイアグラムで表すことを考えよう。例によってただ一つの対象からなる圏\(1\)を用意し、各対象に対してこれから関手を張り、それぞれの射はこの関手間での自然変換とすると、図16になる。
これをpasting diagramで表すと、図17である。
そして、ストリング・ダイアグラムは図18となる。
1.4 結合律・単位律
圏が満たさなければならない条件に結合律と単位律があった。結合律は、\(f:A \rightarrow B, g:B \rightarrow C , f:C \rightarrow D \)が存在したとき、これらを合成しての計算結果は、その結合の順番に寄らないというものである。即ち、\(h(gf))=(hg)f\)である。これをストリング・ダイアグラムで表すと図19となる。
単位律は、恒等射と合成しても変化はないというもので、\(I_B f = f = f I_A \)である。ここで、\(I_A : A \rightarrow A, I_B : B \rightarrow B\)はそれぞれ恒等射である。これをストリング・ダイアグラムで表すと図20となる。
用語説明:モノイド
圏論を勉強し始めて最初に躓いたのが、モノイドである。これは、加算や乗算などの二項演算で単位元を持つものの代数的構造を表す圏である。小学校以来ずっと足し算や掛け算は演算子と習っていて、当然のことこれが射になるものと思っていたら、見事に裏切られた。射になるものは、被加数や加数あるいは被乗数や乗数などの数であって、加算や乗算などの演算はなんと合成であった。
自然数の加算を圏で表現すると下図のようになる。
ここでは、
1) 対象は一つだけで、★で表すことが多い。
2) 射は自然数で、\(a,b,… \in \mathbb{N} \)
3) ドメインとコドメインは★
4) 恒等射は\(0\)
5) 結合は加算( \(+\) )
もちろん、単位律、結合律は満たされている。
集合\(S\)とその上の二項演算\(*: S \times S \rightarrow S\)が与えられ、単位元と結合律を満たすとき、\((S,*)\)の組をモノイド(半群)という。単位元を恒等射、集合を射とすることで、上記のように圏として構成できる。対象が一つの圏(単一対象圏)で、射も集合であることから、これは小さい圏である。また、圏のときは、\(S\)の代わりに、モノイド(Monoid)の頭文字をとってモノイド\((M,*)\)あるいはモノイド\(M\)と記されることが多い。上述の自然数での加算はモノイド\((\mathbb{N},+ )\)となる。
それではモノイド\((\mathbb{N},+ )\)をストリング・ダイアグラムで表すことを考えよう。まずは下図のように関手圏として表す。
つぎに下図のようにpasting diagramにする。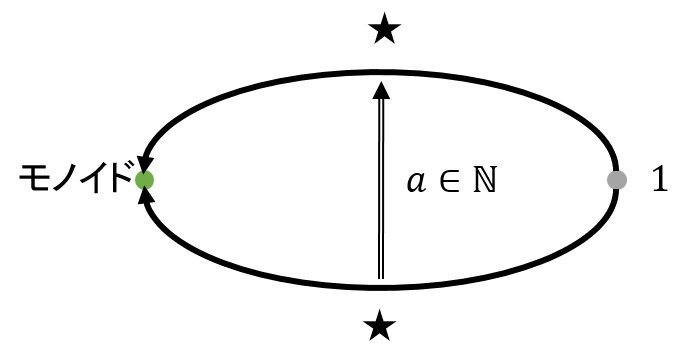
そして下図のようにストリング・ダイアグラムで表す。
最後に、二項演算の場面を下図に示す。