1.7 \( {\rm Hom}\) 関手
圏論らしいと思わせてくれる関手の一つが\( {\rm Hom}\) 関手である。これは射を集合として扱えるようにしてくれる素晴らしい機能である。
1)\( {\rm Hom}\)集合
\( {\rm Hom}\) 関手の説明に先立って\( {\rm Hom}\)集合を説明しよう。二つの対象の間の射の集まりが集合となるとき、これを\( {\rm Hom}\)集合と言う。ドメイン側の対象を\(X\)とし、コドメイン側の対象を\(Y\)としたとき、その\( {\rm Hom}\)集合は\( {\rm Hom}(X,Y)\)と記される。
今ドメイン側の対象\(A\)を固定し、ここから対象\(X,Y\)への\( {\rm Hom}\)集合を\( {\rm Hom}(A,X)\), \( {\rm Hom}(A,Y)\)とし、対象\(X,Y\)での射の一つを\(f: X \rightarrow Y\)としたとき、\( {\rm Hom}(A,X)\)から\( {\rm Hom}(A,Y)\)への\(f\)に対応する射を\( {\rm Hom}(A,f)\)で表す。この射は、ドメインとコドメインとも集合なので、集合での関数となる。
2)\( {\rm Hom}\)関手のドメインとコドメインを構成する圏
それでは、\( {\rm Hom}\) 関手の入口側と出口側の圏について考えよう。入口側の、すなわちドメイン側の圏はちょっと特殊である。この圏ではドメインとコドメインとを結んでいる射の集まりは集合であるという制限を設けている。このような圏は、局所的に小さい圏と一般的に呼ばれている。
次に、\( {\rm Hom}\) 関手の出口側の圏、すなわちコドメイン側の圏について考えよう。この圏は馴染み深い集合の圏である。集合の圏は、1) 対象のそれぞれは集合であり、対象を集めたものは全体の集合となっていて(ラッセルのパラドックスとはならないような集合)、2) 射は対象間の関数の集合であるものをいう。
もう少し詳しく集合の圏を定義すると、対象を\(A,B,…\)としたとき、\(A\),\(B\),\(C\),…のそれぞれは集合であり、それらを集め全体を構成している\( \{A,B,C,…\} \)も集合である。そして、\(A\)から\(B\)への写像を\( {\rm Hom}(A,B) \)としたとき、\( {\rm Hom}(A,B), {\rm Hom}(A,C), {\rm Hom}(B,C)…. \)のそれぞれは集合である。
3)\( {\rm Hom}\)関手の定義
\( {\rm Hom}\)関手の説明に先立って、この関手の役割について言及しておこう。図32に示すように、圏での対象を\(A,X,Y\)とし、\(A\)からそれぞれの対象への射の集合を\( {\rm Hom}(A,X ) \),\( {\rm Hom}(A,Y ) \)とし、\(X\)から\(Y\)への射の一つを\(g:X \rightarrow Y\)としよう。\( {\rm Hom}(A,X ) \),\( {\rm Hom}(A,Y ) \)は集合なので、その間に関数を定義することができる。これには\(g\)を用いて、\( {\rm Hom}(A,g) \)としよう。
関手の役割は、\( {\rm Hom}(A,X ) \),\( {\rm Hom}(A,X ) \),\( {\rm Hom}(A,g) \)を外に放り出し、これらを\(X,Y,g\)で結ぶことである。 
今あげた例は、\(A\)から出ていく射の集合について考えたが、図33に示すように、入ってくるものについても考えることができる。考え方は同じだが、\(Y\)から\(A\)への関数は、\(X\)を経由しての関数の合成となるように、\(g\)の向きを逆転させ、\(g^{op}: Y \rightarrow X\)とし、\( {\rm Hom}(Y,A ) \)から\( {\rm Hom}(X,A ) \)への関数は\( {\rm Hom} (g^{op}, A) \)とする。すなわちすべてが反対となっている世界を定義する。前者では関手が共変となるのに対し、後者は反変となる。 
準備が済んだので、共変関手の方から定義しよう。関手は\( {\rm Hom}_\mathcal{C}(A, - )\)と記される。圏\(\mathcal{C}\)の対象\(X\),\(Y\)と射\(g\)は、この関手によって、圏\(\mathbf{Set}\)の対象\( {\rm Hom}_\mathcal{C} (A,X) \), \( {\rm Hom}_\mathcal{C} (A,Y) \)と射\( {\rm Hom}_\mathcal{C} (A,g) \)に移される。これを図34に示す。 
反変関手の定義は図35になる。ここでは、圏\(\mathcal{C}\) での射の向きを逆にした圏\(\mathcal{C}^{op}\)が使われていることに注意して欲しい。 
4)簡単な例
それではストリング・ダイアグラムで表すことを考えよう。段階的に話を進めるために、まず図36を考えよう。対象は\(A,X\)とし、\( {\rm Hom}_\mathcal{C}(A,A ) \)はその要素に\(a\) を有するとする(実際には恒等射\(I_A\)を始めとする\(A\)から\(A\)への射であるが、ここは集合なので、要素という感触をだすために\(a\)を用いる)。 
例によって圏\(1\)を設け、\(\mathcal{C}\)の対象と射を関手と自然変換するために関手\(A,X\)を張り、さらに\( {\rm Hom}_\mathcal{C}(A,A ) \)の要素\(a\)を表現できるように関手\(*\)を張っておこう。図で示すと37になる。 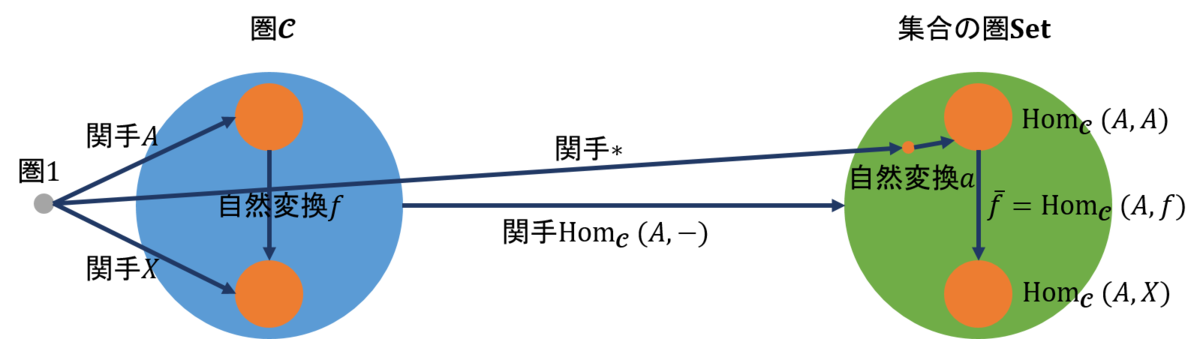
これをpasting diagramで示すと図38となる。 
さらにストリング・ダイアグラムで表すと図39となる。 
反変関手についても同じように議論を進めることができる。これについては読者の方で確認して欲しい。
5)一般的な例
それではもう少し一般的な場合について考えることにしよう。単純な例に対象\(Y\)を付け加え、\(g:X \rightarrow Y\)が与えられたとしよう。
まず共変関手\( {\rm Hom}_\mathcal{C}(A, - ) \)の方から考えることにしよう。図で表すとき、\( {\rm Hom}_\mathcal{C}(A, - ) \)という表記はスペースを必要とするので、これからは\(h^A\)で表すこととする。すると\( {\rm Hom}\) 関手は図40になる。 
圏\(1\)を利用して関手を張ったものが図41である。 
これをpasting diagramで表すと図42となる。 
さらにストリング・ダイアグラムで表すと図43となる。 
それでは次に反変関手\( {\rm Hom}_\mathcal{C}( - ,A ) \)について考えよう。これも同じように\(h_A\)で表すと、圏\(1\)から関手を張った段階は図44となる。 
これよりストリング・ダイアグラムを作成すると図45となる。途中の過程は省略してあるので、共変関手を参考にして途中経過を追って欲しい。 
これで基礎は終わりである。次はいよいよ随伴に進む。