3.集合の世界から圏論の世界へ
ごちゃごちゃしたミクロの世界をかなぐり捨てて雄大なマクロの世界(宇宙)へ旅立つことにしよう。数学でのミクロな世界は集合で、雄大な宇宙は圏論である。集合は、要素の集まりとして定義される。また、集合を論じるときは、それと一緒に関数(あるいは写像)も学んだことと思う。関数は二つの集合を結びつけるものだ。
圏論では、集合に相当するものを対象(object)と呼び、関数に相当するものを射(morphism)と呼ぶ。集合を論じるときは、ミクロな世界なので、その中に含まれている要素がとても重要な役割をする。しかし、圏論では、マクロな世界を論じるので、対象の中身は気にしないことにする。Haskellでは、対象をタイプとして表すが、常に、タイプを気にし、その構成要素に対してはたいして注意を払わない。
今回の記事では、集合を捨てて対象に、関数を捨てて射に、乗り移れるための準備をしよう(Haskellでは、射を関数と呼んでいるので、少しごちゃごちゃするのだが、Haskellで関数といっているときは、圏論での射と思って欲しい)。
3.1 関数とは
物事を始めるにあたっては、その中で用いる用語の意味をはっきりさせておく必要がある。そこで、ここでは、関数とは何かをはっきりさせておこう。これは、射との違いを考えるうえで助かるはずだ。
少し、基礎的な概念から始めてみよう。プログラムを書くからには、そこに何らかの意思あるいは意図があるはずである。出来上がったプログラムは、そこに、作者の意思あるいは意図を実現しているはずである。そこで、プログラムを書く際に、どのようにして、意思や意味を埋め込んでいくのかが重要になる。
JavaやCのような命令型(imperative)のプログラミング言語を用いれば、意思や意図は、「プログラムのシークエンス(how)」として埋め込まれることになる。HaskellやPrologのような宣言型(declarative)のプログラミング言語を用いれば、それらは「どのようなものであるか(what)」として埋め込まれることになる。
宣言型の説明のところが分かりにくいので、補足しておいた方がよいと思う。プログラムはある特定の領域あるいは特定の問題を対象にして記述される。特定の領域には、それを細かく分解していくと、それ以上は分解できない構成要素(atom)が出てくる。そこで、構成要素の性質あるいは性格をプログラムとして記述する。分解したのとは逆に構成要素を用いて組み立てていくと元の領域に戻るはずである。この作業は構成要素を記述したプログラムの合成で実現する。
例えば、量子力学の世界を考えると、最小の単位は粒子である。これは、数学的にはケットとブラと表すことができる。そこで、ケットとブラを対象(データ型)として表す。ケットとブラに成り立っている関係を射(関数)とその合成で表すことで、量子力学の世界をプログラムで提供できるようになる。
通常、コンピュータ科学の世界では、意思や意図は、意味という。命令型のプログラミング言語を用いて意味を表す方法を操作的意味論(operational semantics)といい、宣言型に対しては表示的意味論(denotational semantics)という。表示的という言葉が使われているのは、構成要素をその特定領域での言葉を用いて表現しているということによる。
1)関係
それでは、表示的意味論での実際的な例を考えることにしよう。代表的なものは、そして、最も多くの場面で使われるのは、関係(relation)だろう。通常の文章でもよく出てくるし、コンピュータの世界でも、データベースでは基本的な概念になっている。例えば、合コンをした時に、望ましいと思った異性をあげることは一つの関係を表している。
ある男性は、一人の女性を望ましいと思ったかもしれない。また、別の男性は、気が多いのか、複数の女性を考えたかもしれない。また、さらに別の男性は、好みがうるさいのか、誰もいなかったというかもしれない。逆に女性側から見たときも、同じようなことが起こる。とても運がよい場合には、二人の好みが合致する場合もある。このような関係を示したのが次の図だ。

数学では、関係は直積集合(Cartesian product)で表される。例えば、次のようになる。男性の方から女性を望ましいと思う関係は、例えば、次のように表される。
\begin{eqnarray}
(Peter, Marry) \\
(Peter, Betty) \\
(Mike, Ellen) \\
(Tom, Michell)
\end{eqnarray}
コンピュータでは、関係は、多くの場合、前述したようにデータベースとして表される。
2)関数
関係は、とても一般的で、二つのグループの関わり合いを形式的に記述するのに都合がよい。しかし、あまりにも自由度が大きすぎるため、数学的な枠組みで使おうとするときは、もう少し、制限の強い概念を用いたほうが都合のよいことが多い。これが関数と呼ばれる。関数は、ドメイン(domain)とコドマイン(codomain)の関係を表すが、そこには、いくつかの約束事がある。
1) 関数には方向性がある。ドメインとコドメインの関係は対等ではなく、矢印がドメインからコドメインの方に向かっている。
2) ドメインの全ての要素に対して、コドマインのある一つの要素が対応する。先ほどの合コンでの例で、好ましい女性がいなかったという男性がいたが、このようなことは許されず、全ての男性は好ましい女性がいなくてはならない。また、複数の女性を好ましいと思う男性がいたがこのようなことも許されない。但し、一人の女性に対して、複数の男性が好ましいと思うこと(多対一対応)は許される。

次の例は、全ての男性が女性一人だけを望ましいといっているので、この関係は関数となる。コドメインの中で、相手のある要素の集まりをイメージという。これらの関係を図で示すと次のようになる。

ドメインの全ての要素に対して相手が割り当てられているような関数を全関数(total function)という。これに対して、ドメインのあるものに対しては相手が割り当てられていないような関数を部分関数(partial function)という。これから扱うすべての関数は全関数である。関数でないものの例を以下に示す。

また、関数の値は変わることがない。このような関数を純粋関数(pure function)という(日本語では純粋関数という用語は使わないようだがここでは便宜的に使う。純粋関数型言語という使い方はあるが、それ以外で使われる例はないようである)。人間の脳は純粋関数ではない。相手に対する好き嫌いは、様々な経験を通して、変化することが往々にしてある。このため、一定であるという保証をすることはできない。一般に、記憶を持つようなものは純粋関数にはならない。
3)逆関数
先ほどは、男性の方から好ましい女性を示す関数\(f\)について説明した。それでは、女性の方から好ましい男性を示す関数\(g\)を考えてみよう。
そこで、関数\(f\)を使って望ましい女性を得た後、関数\(g\)を使ってその女性が、好ましいと思っている男性を求めてみることにしよう。もし、その結果が自身に戻ってくるんであれば、お互いに好ましいと思っているので、こんなに嬉しいことはない。もしすべての男性について、自身に戻ってくるようであれば、男性たちはとても幸せだろう。
逆に、女性の方からも考えてみよう。その場合には、関数\(g\)を施した後で、関数\(f\)を施すことになる。やはり、全ての女性について、自身に戻ってくるようであれば、女性たちはとても幸せだろう。
このようなことが、男性にも、女性にも起こっているとすると、この合コンは理想的な結果をもたらしたといえるだろう。
このことを数学的に記述すると、男性の場合には、
\begin{eqnarray}
g \circ f = id_M
\end{eqnarray}
女性の場合には、
\begin{eqnarray}
f \circ g = id_F
\end{eqnarray}
となる。ここで、\(id_M\)は男性のグループに対する恒等写像、\(id_F\)は女性のグループに対する恒等写像である。
圏論での用語を用いて上記を記述しなおすと、
1) 対象:\(M\)(男性のグループ)、\(F\)(女性のグループ)
2) 射:\(f:M \rightarrow F\)(好ましい女性への射)、\(g:F \rightarrow M\)(好ましい男性への射)
3) 恒等射:\(id_M\)(男性のグループでの恒等射)、\(id_F\)(女性のグループでの恒等射)
4) 合成:\(g \circ f\)、\(f \circ g\)
【圏論の世界での同型写像の定義】
一般に、
\begin{eqnarray}
f:M &\rightarrow & F\\
g:F &\rightarrow & M\\
g \circ f &=& id_M \\
f \circ g &=& id_F
\end{eqnarray}
が成り立つとき、\(f\)と\(g\)は同型写像であるという。数学の概念の中では、重要な概念の一つである。
ここでのポイントは、合成\(\circ\)と恒等射\(id\)を用いて、同型写像が定義されていることである。
上記では、\(M,F,f,g\)について具体的な例を挙げて説明したが、これらはどのようなもので置き換えてもよい。その時、上記のような関係が成り立つとき、\(f\)と\(g\)は同型写像という。また、\(M\)と\(F\)は同型という。
圏論による同型写像の定義の重要性は、対象の要素については何も問うていないことである。細かいことは気にしなくてもよいといっている。また、写像が射に変わっている点である。射は写像を超えるもっと普遍的な概念である。このため、より抽象的な同型を定義するのに役立つ(後々、関手(functor)の話をするがこれは写像をより一般化したものである)。
同型写像は、対象同士が対称(symmetric)であると教えてくれる。あるいは、行って戻れる、すなわち、可逆的(invertible)であるとも知らせてくれる。
同型写像は変化のないモノトーンの世界なのだが、世の中でこのようなことが成り立つことは少ない。同型写像にならない条件は次の通りである。
1) 対象のサイズが異なる。先の合コンの場合、男性と女性の数が異なる場合には、1対1のペアを作ろうとしても、数の多い性の人の誰かが余ってしまう。
2) 多対一対応のものがある。即ち、コドメインのある要素が、二つ以上のドメインの要素から写像される。即ち、\(\exists a, \exists b, a \neq b, f(a) = f(b)\)である。この場合には、二人以上の男性からある女性が望ましいと思われても、その女性は一人の男性しか望ましいと思えないので、破綻してしまうこととなる。
【圏論の世界での逆写像の定義】
関数\(f\)と\(g\)が同型写像である時、\(g\)は\(f\)の逆関数であるという。\(f\)の逆関数は\(f^{-1}\)と書く。同様に、\(f\)は\(g\)の逆関数であるという。
逆関数の例を挙げておこう。今、自然数(0から始まる)と奇数(1から始まる)のグループを考えることにする。自然数のグループの方が奇数のそれよりも2倍だけサイスが大きいと考えがちだが、そんなことはない。

自然数\(x\)から奇数\(y\)への写像\(f\)を\(y=f(x)=2x+1\)とし、奇数から自然数への写像\(g\)を\(x=g(y)=(y-1)/2\)とすると、
\begin{eqnarray}
g \circ f &=& id_\mathbb{ N } \\
f \circ g &=& id_{Odd}
\end{eqnarray}
が成り立つ。
このことから、自然数と奇数は同型であることが分かる。奇数は自然数の部分集合だと思うとなんか変な気分になる。要素の数が無限の時、往々にして、直感が働かない時があるが、これはその例の一つである。
4)全射と単射
圏論の世界から、もう一度、集合の世界に戻ってみよう。この世界では、集合の要素同士がどのように写像されているかが、重要な話題だ。その中から、全射(surjective)と単射(injective)に登場してもらおう。
Surjectiveという単語は、日常会話で用いることはまずないので、初めて見たという人も多いことと思う。この単語は、surとjectiveをつなげたもので、surは、surfaceからも連想できるように、「上」という意味を持つ。語源は古フランス語だ。また、jectは「投げる(の過去分詞)」を意味し、ラテン語を語源としている。
従って、Surjectiveは形容詞「上に投げられた」となる。これに対応した全射という日本語訳もあまり好きではないのだが、関数\(f:A \rightarrow B\)のイメージ\(f(A)\)とコドメイン\(B\)が一致するとき、即ち\(f(A) = B\)のとき、関数\(f\)は全射であるという。
Injectiveは同じようにinとjectiveの合成語である。inは「中へ」という意味だが、この場合には、「そのまま中へ」という意味が含まれているのであろう。別の要素は別の要素へ移すというニュアンスで用いられている。従って、ドメインの任意の二要素\(a,b\)に対して\(a \neq b\)の時、\(f(a) \neq f (b) \)が成り立つならば、関数\(f\)は単射であるという。
集合の世界では、この二つの用語を用いて、先ほどの同型写像が定義される。
【集合の世界での同型写像の定義】
関数\(f:A \rightarrow B \)が、全射で単射である時、\(f\)は同型写像であるという。
【集合の世界での逆写像の定義】
関数\(f\)が同型写像である時、その矢印の向きを反対にした写像を\(f\)の逆写像という。これを\(f^{-1}\)と記す。
皆さんは、集合の上に定義された同型写像と、圏論の上でのそれとではどちらが好きだろうか。集合の上での定義はアセンブリ言語による定義で、圏論の上での定義は高級言語でのそれに相当すると思うのだが、どうだろうか。
5)エピ射とモノ射
同型写像と逆写像を圏論の世界と集合の世界でそれぞれ定義したので、全射と単射についても圏論の世界で定義してみよう。
まず、全射の方から始める。集合の世界はラテン系の言語を語源としていたので、圏論ではギリシャ系の語源を用いることで、用語も変えてみることとする。ラテン系のチャラチャラした世界からギリシャ系の哲学の世界へ移ろうというと物議を醸しそうだが、気分としてはそんなところだ。surに対応するギリシャ語はepiである。そこで、全射をエピ射(epimorphism)ということにしよう。
また、単射の方は、単一を表すギリシャ語monoを用いてモノ射(monomorophism)ということにする。
それでは、エピ射を定義してみよう。
エピ射でないとすると下図のようなことが発生する。
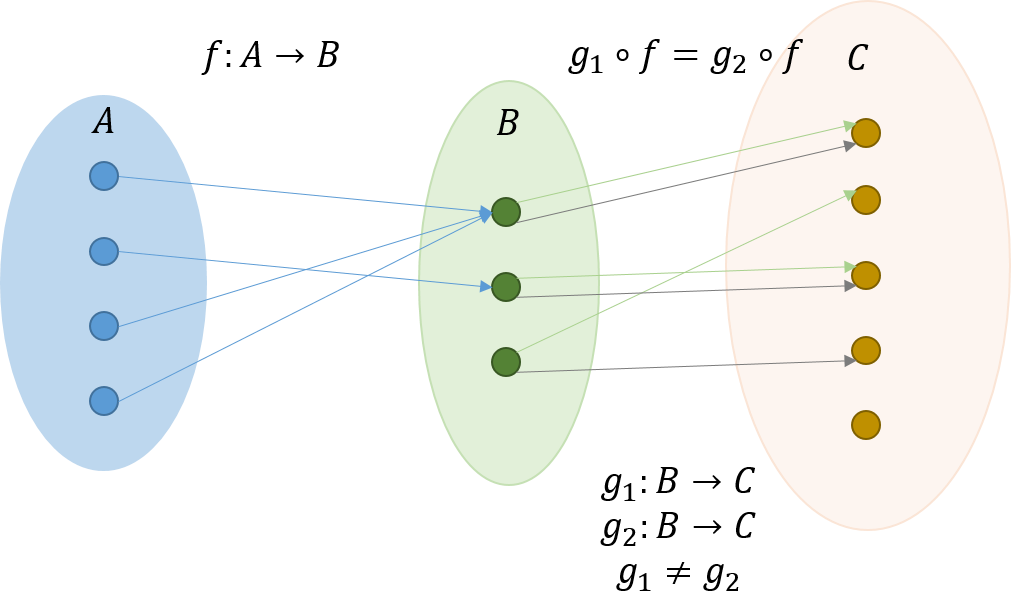
今、射\(f:A \rightarrow B \)がエピ射でないとする。この時、
\begin{eqnarray}
(g_1 \circ f = g_2 \circ f) \land (g_1 \neq g_2)
\end{eqnarray}
を成り立たせるある対象\(C\)と二つのある射\(g_1: B \rightarrow C\)と\(g_2: B \rightarrow C\)が存在する。
(上の記述を論理式で念のために表しておこう。
\begin{eqnarray}
\exists C,\exists g_1(g_1: B \rightarrow C),\exists g_2(g_2: B \rightarrow C) \\
f(f:A \rightarrow B) \notin Epimorphisms \Rightarrow \\
(g_1 \circ f = g_2 \circ f) \land (g_1 \neq g_2)
\end{eqnarray}
)
そこで、この対偶を取ってみよう。次のようになる(飛躍しすぎだと思う人は、上記の論理式より導き出してほしい)。
全ての対象\(C\)と全ての二つの射\(g_1\)と\(g_2\)に対して
\begin{eqnarray}
(g_1 \circ f \neq g_2 \circ f) \lor (g_1 = g_2)
\end{eqnarray}
の時、射\(f:A \rightarrow B \)はエピ射となる。
そこで、
\begin{eqnarray}
(g_1 \circ f \neq g_2 \circ f) \lor (g_1 = g_2)
\end{eqnarray}
の部分は次のように変えることができる。
\begin{eqnarray}
(g_1 \circ f = g_2 \circ f) \Rightarrow (g_1 = g_2)
\end{eqnarray}
これを利用して次のように定義することができる。
【エピ射の定義】
射\(f:A \rightarrow B \)が次の条件を満たす時、エピ射という。
条件:全ての対象\(C\)と全ての二つの射\(g_1: B \rightarrow C\)と\(g_2: B \rightarrow C\)に対して、
\begin{eqnarray}
g_1 \circ f = g_2 \circ f
\end{eqnarray}
が成り立つとき、
\begin{eqnarray}
g_1 = g_2
\end{eqnarray}
である。[条件終了]
モノ射については、同じように考える。

今、射\(f:A \rightarrow B \)が上図に示すようにモノ射でないとする(上図では異なる矢印のみを記してある。記してない部分は、二つの矢印とも同じ場所から出発して同じ場所にたどり着くので、適当に補って考えること)。この時、
\begin{eqnarray}
(f \circ g_1 = f \circ g_2) \land (g_1 \neq g_2)
\end{eqnarray}
を成り立たせるある対象\(C\)と二つのある射\(g_1: C \rightarrow A\)と\(g_2: C \rightarrow A\)が存在する。
そこで、この対偶を取る。次のようになる。
全ての対象\(C\)と全ての二つの射\(g_1\)と\(g_2\)に対して
\begin{eqnarray}
(f \circ g_1 \neq f \circ g_2) \lor (g_1 = g_2)
\end{eqnarray}
の時、射\(f:A \rightarrow B \)はモノ射となる。
そこで、
\begin{eqnarray}
(f \circ g_1 \neq f \circ g_2) \lor (g_1 = g_2)
\end{eqnarray}
の部分は次のように変えることができる。
\begin{eqnarray}
(f \circ g_1 = f \circ g_2) \Rightarrow (g_1 = g_2)
\end{eqnarray}
これを利用して次のように定義することができる。
【モノ射の定義】
射\(f:A \rightarrow B \)が次の条件を満たす時、モノ射という。
条件:全ての対象\(C\)と全ての二つの射\(g_1: C \rightarrow A\)と\(g_2: C \rightarrow A\)に対して、
\begin{eqnarray}
f \circ g_1 = f \circ g_2
\end{eqnarray}
が成り立つとき、
\begin{eqnarray}
g_1 = g_2
\end{eqnarray}
である。[条件終了]
エピ射、モノ射とも対象の要素を使うことなく、関数の合成だけで定義しているところが大きな特徴である。集合でのそれと比べてどうであろうか。すっきりと見えるのではないだろうか。
追伸
エピ射もモノ射も全ての\(C\),\(g_1\),\(g_2\)に対してといっている。宇宙に存在するものすべてからだと、いつ証明が済むのかなと思ってします。これに代わるものを用意しておいて、この対象とこの射について調べてくれればいいよというものがあると助かる。そこで、これらを用意することにしよう。
モノ射:対象はシングルトンの空間、即ち、\(C=()\)とする。射は、\(A\)の各要素への写像、即ち、\(g_a:() \rightarrow a \in A\)とする。
エピ射:対象は2要素からなる空間、即ち、\(C=\{c_1,c_2\}\)とする。射は、\(B\)を2分し、一方を対象の一つに、他方を対象の残りに写像する、即ち、\(g_{B'}: (B' \subset B \rightarrow c_1 \lor B-B' \rightarrow c_2) \)とする。これの目的は次のようである。対象を2分し、別々の値に写像することで、全ての関数が異なるようになる。なお、\(C\)はブール値の集合\(\{true,false\}\)と考えてもよい。
