今年の秋は、天候に恵まれ、秋たけなわの日が多い。先日、伊豆の稲取にある細田高原を訪れた。かっては、茅葺屋根の材料となる茅の産地としてこの地方の産業を支えていたそうである。箱根の仙石原の7倍はあるすすき畑を観光地にしようということで開発を促進しているとのことである。見事なほどのすすきの草原が広がっていた。秋を楽しんでいるうちにブログの方がおろそかになったが、ビリヤード台で衝突するプログラムの完成に取り掛かることとする。
10.2 衝突後の位置を求める
ボールの衝突を記述しやすくするために、これまで、二つの座標系を導入してきた。今回は、さらに、もう一つの座標系を用意するが、これまでのおさらいをしておこう。
ビリヤード座標系では、ビリヤード台の中心部を原点とし、台の横方向を\(x\)座標、縦方向を\(y\)座標とした座標系である。二つのボールの位置はベクトルで表わした。時間\(t_0\)での位置はそれぞれ\(\vec{p_1},\vec{p_2}\)、時間\(t_0+dt\)ではそれぞれ\(\vec{p'_1},\vec{p'_2}\)とする。また、速度もベクトルで表し、\(t_0\)ではそれぞれ\(\vec{v_1},\vec{v_2}\)、\(t_0+dt\)ではそれぞれ\(\vec{v'_1},\vec{v'_2}\)とする。また、それぞれ、質量は\(m_1,m_2\)、半径は\(r_1,r_2\)である。さらに、\(t_0\)と\(t_0+dt\)の間で二つのボールは衝突する。衝突するまでの二つのボールの動きを示したのが下図である。
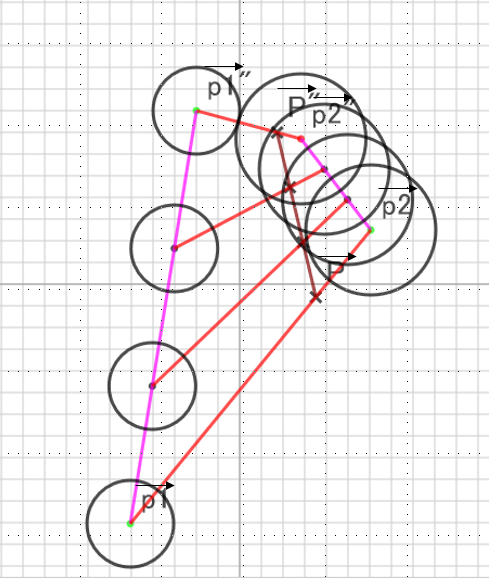
次に導入したのが、重心座標系である。これは、二つのボールの重心に座標系を平行移動したものである。この座標系でのボールの位置と速度は次のように表す。時間\(t_0\)での位置は、それぞれ\(\vec{q_1},\vec{q_2}\)、時間\(t_0+dt\)ではそれぞれ\(\vec{q'_1},\vec{q'_2}\)とする。また、速度は、\(t_0\)ではそれぞれ\(\vec{w_1},\vec{w_2}\)、\(t_0+dt\)ではそれぞれ\(\vec{w'_1},\vec{w'_2}\)とする。
このとき、ビリヤード座標系での重心の位置は、\(t_0\)で\({\vec P} = \frac{m_1 \times {\vec p_1} + m_2 \times {\vec p_2}}{m_1+m_2}\)であり、\(t_0+dt\)で\({\vec P'} = \frac{m_1 \times {\vec p'_1} + m_2 \times {\vec p'_2}}{m_1+m_2}\)である。また、重心の速度は時間に関係なく、\({\vec V}= \frac{m_1 \times {\vec v_1} + m_2 \times {\vec v_2}}{m_1+m_2}\)である。
重心座標系で見た二つのボールの運動は下図のようになる。二つのボールは並行した線の上をお互いに反対方向から侵入し、衝突したあと、別の平行線の上を離れていく。

二つの座標系の位置と速度の関係は次のようになる。
\({\vec q_1}={\vec p_1}-{\vec P}\)
\({\vec q_2}={\vec p_2}-{\vec P}\)
\({\vec q'_1}={\vec p'_1}-{\vec P'}\)
\({\vec q'_2}={\vec p'_2}-{\vec P'}\)
\({\vec w_1}={\vec v_1}-{\vec V}\)
\({\vec w_2}={\vec v_2}-{\vec V}\)
\({\vec w'_1}={\vec v'_1}-{\vec V}\)
\({\vec w'_2}={\vec v'_2}-{\vec V}\)
また、重心座標系では衝突した後でも、それぞれの速さは変わらない。即ち、次の式が成り立つ。
\(|{\vec w_1}|=|{\vec w'_1}|\)
\(|{\vec w_2}|=|{\vec w'_2}|\)
二つのボールが衝突する前の平行線の傾き\(\theta\)は速度の方向なので、
\begin{eqnarray}
{\rm tan} \theta = \frac {w_{1,y'}} {w_{1,x'}}
& = & \frac {w_{2,y'}} {w_{2,x'}} \\
& = & \frac{v_{1,y}-v_{2,y}}{v_{1,x}-v_{2,x}} \\
& = & \frac{dv_y}{dv_x}
\end{eqnarray}
である。なお、重心座標系での横軸を\(x'\)、縦軸を\(y'\)とする。また、
\begin{eqnarray}
dv_x & = & v_{1,x}-v_{2,x}, \\
dv_y & = & v_{1,y}-v_{2,y}, \\
dv & = & \sqrt{dv_x^2+dv_y^2}
\end{eqnarray}
である。
次に、衝突時の衝突した点(二つのボールの接点)での接線\(ST\)の傾き\(\varphi\)を求める。
衝突したときの二つのボールの中心を\(A,B\)とする。また、\(A\)から、\(B\)を通る接線\(ST\)に平行な線へ、垂直に垂らした点を\(C\)とする。このとき、\(\triangle ABC\)は\(\triangle EAD\)と相似である。\(\angle DEA\)が\(\varphi - \theta\)であることから、\(\angle CAB\)は\(\varphi - \theta\)となる。辺\(AB\)の長さは\(r_1+r_2\)である。また、辺\(AC\)の長さを辺\(l\)とすると、\({\rm cos}(\varphi - \theta)=\frac{l}{r_1+r_2}\)となる。

\(l\)の長さは次のように求められる。衝突時のボールの中心\(A\)を通る、接線\(ST\)に平行な線を\(y'= {\rm tan} \theta \times x' + c\)とする。ここで、\(c= q_{1,y'}-{\rm tan} \theta \times q_{1,x'}\)である。ボールの中心\(B\)に対しても平行な線を\(y'= {\rm tan} \theta \times x' + c'\)とする。ここで、\(c'= q_{2,y'}-{\rm tan} \theta \times q_{2,x'}\)である。二つの平行線の距離は\(\frac{切片の差}{\sqrt{傾き^2 + 1}}\)で得られることが知られているので、\(l = \frac{|c-c'|}{\sqrt{{\rm tan}^2 \theta + 1}} = | {\rm cos} \theta \times (p_{1,y}-p_{2,y})-{\rm sin} \theta \times (p_{1,x}-p_{2,x})| \)となる。
\(\varphi\)は次のようにして求めることができる(但し、重心からみて二つのボールとも時計回りに動いている)。
\begin{eqnarray}
{\rm cos} \varphi& = & {\rm cos} ( \varphi - \theta + \theta ) \\
& = & {\rm cos}( \varphi - \theta ){\rm cos} \theta - {\rm sin}( \varphi - \theta ){\rm sin} \theta \\
& = & \frac {l}{r} \frac{dv_x}{dv}-\frac {\sqrt{r^2-l^2}}{r} \frac{dv_y}{dv}
\end{eqnarray}
\begin{eqnarray}
{\rm sin} \varphi& = & {\rm sin} ( \varphi - \theta + \theta ) \\
& = & {\rm sin}( \varphi - \theta ){\rm cos} \theta + {\rm cos}( \varphi - \theta ){\rm sin} \theta \\
& = & \frac {\sqrt{r^2-l^2}}{r} \frac{dv_x}{dv}+\frac {l}{r} \frac{dv_y}{dv}
\end{eqnarray}
ここで、\(r=r_1+r_2\)である。
左のボールが反時計回りに動いている場合は下図を参考にすると次のようになる。

\begin{eqnarray}
{\rm cos} \varphi& = & {\rm cos} ( \varphi - \theta + \theta ) \\
& = & {\rm cos}( \varphi - \theta ){\rm cos} \theta - {\rm sin}( \varphi - \theta ){\rm sin} \theta \\
& = & {\rm cos}( \theta - \varphi ){\rm cos} \theta + {\rm sin}( \theta - \varphi ){\rm sin} \theta \\
& = & \frac {l}{r} \frac{dv_x}{dv}+\frac {\sqrt{r^2-l^2}}{r} \frac{dv_y}{dv}
\end{eqnarray}
\begin{eqnarray}
{\rm sin} \varphi& = & {\rm sin} ( \varphi - \theta + \theta ) \\
& = & {\rm sin}( \varphi - \theta ){\rm cos} \theta + {\rm cos}( \varphi - \theta ){\rm sin} \theta \\
& = & -{\rm sin}( \theta - \varphi ){\rm cos} \theta + {\rm cos}( \theta - \varphi ){\rm sin} \theta \\
& = & -\frac {\sqrt{r^2-l^2}}{r} \frac{dv_x}{dv}+\frac {l}{r} \frac{dv_y}{dv}
\end{eqnarray}
平行線の傾きが正の場合で示したが、負の場合も同様で下図のようになる。

最後に、二つのボールが一直線上の上を移動しているときの接線\(\varphi\)を求める。\(0<\theta < \frac{\pi}{2}\)のとき、\(\varphi=\theta + \frac{\pi}{2}\)である。これより、
\begin{eqnarray}
{\rm cos} \varphi& = & {\rm cos} (\theta +\frac{\pi}{2} ) = -{\rm sin} \theta = -\frac{dv_y}{dv}\\
{\rm sin} \varphi& = & {\rm sin} (\theta +\frac{\pi}{2} ) = {\rm cos} \theta = \frac{dv_x}{dv}
\end{eqnarray}
また、\(\frac{\pi}{2} \le \theta < \pi\)のとき、\(\varphi=\theta - \frac{\pi}{2}\)である。これより、
\begin{eqnarray}
{\rm cos} \varphi& = & {\rm cos} (\theta - \frac{\pi}{2} ) = {\rm sin} \theta = \frac{dv_y}{dv}\\
{\rm sin} \varphi& = & {\rm sin} (\theta - \frac{\pi}{2} ) = -{\rm cos} \theta = - \frac{dv_x}{dv}
\end{eqnarray}
さて、おさらいが終了したので、次の座標系を考える。これは回転座標系となずける。次のようにして得る。重心座標系を重心を中心にして、衝突した点での接線\(ST\)が水平になるように回転する。上記の図に対しては下図のものが得られる。この座標系での横軸を\(\alpha\)、縦軸を\(\beta\)とする。

重心座標系と回転座標系の関係は次のようになる(接線の傾き\(\varphi\)だけ時計回りの方向に回転させればよい)。
\begin{equation}
\begin{pmatrix}
\alpha \\ \beta
\end{pmatrix}
=
\begin{pmatrix}
{\rm cos} (-\varphi) & {\rm -sin} (-\varphi) \\
{\rm sin} (-\varphi) & {\rm cos} (-\varphi)
\end{pmatrix}
\begin{pmatrix}
x' \\ y'
\end{pmatrix}
\end{equation}
書き直すと次のようになる。
\begin{equation}
\begin{pmatrix}
\alpha \\ \beta
\end{pmatrix}
=
\begin{pmatrix}
{\rm cos} \varphi & {\rm sin} \varphi \\
{\rm -sin} \varphi & {\rm cos} \varphi
\end{pmatrix}
\begin{pmatrix}
x' \\ y'
\end{pmatrix}
\end{equation}
この座標系でのボールの位置と速度は次のように表す。時間\(t_0\)での位置はそれぞれ\(\vec{s_1}=(\alpha_1,\beta_1),\vec{s_2}=(\alpha_2,\beta_2)\)、時間\(t_0+dt\)ではそれぞれ\(\vec{s'_1},\vec{s'_2}\)とする。また、速度は、\(t_0\)ではそれぞれ\(\vec{u_1}, \vec{u_2}\)、\(t_0+dt\)ではそれぞれ\(\vec{u'_1},\vec{u'_2}\)とする。
また、重心座標系では衝突した後も速さが変わらなかった。この性質は、回転座標系でも維持されるので、次が成り立つ。
\(|{\vec u_1}|=|{\vec u'_1}|\)
\(|{\vec u_2}|=|{\vec u'_2}|\)
また、衝突した時点での、ボールの中心の位置をそれぞれ\(\vec{s''_1},\vec{s''_2}\)とする。ボールが衝突しているときの重心から衝突点への高さ\(d\)を求める。衝突点から重心の位置を求めると、\(\frac{m_1 \times r_1+m_2 \times (-r_2)}{m_1+m_2}\)である。方向が反対なので符号を入れ替えると、\(d=\frac{-m_1r_1+m_2r_2}{m_1+m_2}\)を得る。これより、\(\vec{s''_1}=(0,d+r_1),\vec{s''_2}=(0,d-r_2)\)を得る。
\(t+dt\)の時間でのボールの位置を求める。ボールは衝突した後、まるで鏡の面で光が反射されたかのように、入射角と反射角(衝突後の角度)を同じにして、速さを維持したまま進んでいく。従って、回転座標系では、衝突すると、\(\beta\)方向の速度の符号が入れ替わる。\(\alpha\)方向は同じである。図を参考にして、

これより、
\begin{equation}
\vec{s'_1}=(\alpha_1 +dt \times u_{\alpha_1},2(d+r_1)-(\beta_1+ dt \times u_{\beta_1})), \\
\vec{s'_2}=(\alpha_2 +dt \times u_{\alpha_2},2(d-r_2)-(\beta_2+ dt \times u_{\beta_2}))
\end{equation}
これで、衝突後のボールの位置を求めることができた。