10.ビリヤード台で衝突するボール
今までは、一直線上の二つのボールが衝突する現象を扱ってきたが、ここではビリヤード台のような長方形の箱の中で運動する二つのボールの衝突について扱うこととする。
10.1 原理
二つのボールは前と同じように等速で運動するものとするが、二つのボールは大きさや重さが異なってもいいものとする。しかし、問題を簡単にするためにボールの中心は常に同じ高さにあるものとする(現実のビリヤード台だと、ボールの大きさが異なるとその中心の位置も異なるが、ここでは、この点は無視する)。また、衝突したとき運動のエネルギーは保たれるものとする。
二つのボールの質量をそれぞれ\(m_1\),\(m_2\)、半径を\(r_1\),\(r_2\)とする。時間\(t_0\)でのそれぞれの位置を\({\vec p_1}\),\({\vec p_2}\)、速度を\({\vec v_1}\),\({\vec v_2}\)とする。また、時間間隔\(dt\)が過ぎたときの時間\(t_1=t_0 + dt\)でのそれぞれの位置を\({\vec p'_1}\),\({\vec p'_2}\)、速度を\({\vec v'_1}\),\({\vec v'_2}\)とする。位置、速度ともにベクトルで表す。
この時、運動量は保存されるので、
\(m_1 \times {\vec v_1} + m_2 \times {\vec v_2}= m_1 \times {\vec v'_1} + m_2 \times {\vec v'_2}\)
である。
また、運動エネルギーも保存されるので、
\(\frac{m_1 \times {|{\vec v_1}|}^2}{2} + \frac{m_2 \times {|{\vec v_2}|}^2}{2}=\frac{m_1 \times {|{\vec {v'}_1}|}^2}{2} + \frac{m_2 \times {|{\vec {v'}_2}|}^2}{2} \)
である。
ここで、一直線上で衝突するボールで説明したときと同じように、二つのボールを一つのものとみなしたとき、時間\(t_0\)での二つのボールの重心の位置は、\({\vec P_0} = \frac{m_1 \times {\vec p_1} + m_2 \times {\vec p_2}}{m_1+m_2}\)であり、重心の速度は\({\vec V_0} = \frac{m_1 \times {\vec v_1} + m_2 \times {\vec v_2}}{m_1+m_2}\)となる(重心の速度の方は運動量が変わらないことから、\(m_2 \times {\vec v_1} + m_1 \times {\vec v_2} =(m_1+m_2) \times {\vec V_0}\)が成り立ち、これから速度\({\vec V_0}\)が求まる)。また、\(t_1=t_0 + dt\)での重心の速度\({\vec V_1}\)は\( \frac{m_1 \times {\vec v'_1} + m_2 \times {\vec v'_2}}{m_1+m_2}\)である。
\(m_1 \times {\vec v_1} + m_2 \times {\vec v_2}= m_1 \times {\vec v'_1} + m_2 \times {\vec v'_2}\)であることから、\({\vec V_1}={\vec V_0}\)である。従って、重心の速度は衝突に影響されない。そこで、重心の速度は\({\vec V}\)で表す(もちろん、\({\vec V}={\vec V_0}={\vec V_1}\)である)。
ここで、原点を重心に平行移動した座標系を考える(これを重心座標系と名付ける。今までの座標系をビリアード台座標系とする)。\(t_0\)でのボールの位置を\({\vec q_1}\),\({\vec q_2}\)とし、速度を\({\vec w_1}\),\({\vec w_2}\)とする。また、\(t_1=t_0+dt\)でのボールの位置を\({\vec q'_1}\),\({\vec q'_2}\)とし、速度を\({\vec w'_1}\),\({\vec w'_2}\)ととする。
二つの座標系の関係を図で示す。

重心座標系でのそれぞれのボールの位置と速度は、ビリヤード台座標系のそれらを用いて得ることができる。
\({\vec q_1}={\vec p_1}-{\vec P}\)
\({\vec q_2}={\vec p_2}-{\vec P}\)
\({\vec q'_1}={\vec p'_1}-{\vec P'}\)
\({\vec q'_2}={\vec p'_2}-{\vec P'}\)
\({\vec w_1}={\vec v_1}-{\vec V}\)
\({\vec w_2}={\vec v_2}-{\vec V}\)
\({\vec w'_1}={\vec v'_1}-{\vec V}\)
\({\vec w'_2}={\vec v'_2}-{\vec V}\)
重心座標系でも、運動量は保存されるので、
\(m_1 \times {\vec w_1} + m_2 \times {\vec w_2}= m_1 \times {\vec w'_1} + m_2 \times {\vec w'_2}\)
である。この時、重心は常に原点にあるので、上記の式は\(m_1 \times {\vec w_1} + m_2 \times {\vec w_2}= m_1 \times {\vec w'_1} + m_2 \times {\vec w'_2}=0\)となる。これより、
\({\vec w_1} = -\frac{m_2}{m_1} \times {\vec w_2}\)
\({\vec w'_1} = -\frac{m_2}{m_1} \times {\vec w'_2}\)
となる。
また、運動エネルギーも保存されるので、
\(\frac{m_1 \times {|{\vec w_1}|}^2}{2} + \frac{m_2 \times {|{\vec w_2}|}^2}{2}=\frac{m_1 \times {|{\vec {w'}_1}|}^2}{2} + \frac{m_2 \times {|{\vec {w'}_2}|}^2}{2} \)
である。この式と、運動量で求められた式を利用すると
\(|{\vec w_1}|=|{\vec w'_1}|\)
\(|{\vec w_2}|=|{\vec w'_2}|\)
が得られる。なお、ここで、\(|{\vec w}|\)は速さ(スカラー)で、\({\vec w}\)は速度(ベクトル)である。これより、衝突後の速さは重心座標系では変化しないことが分かる。
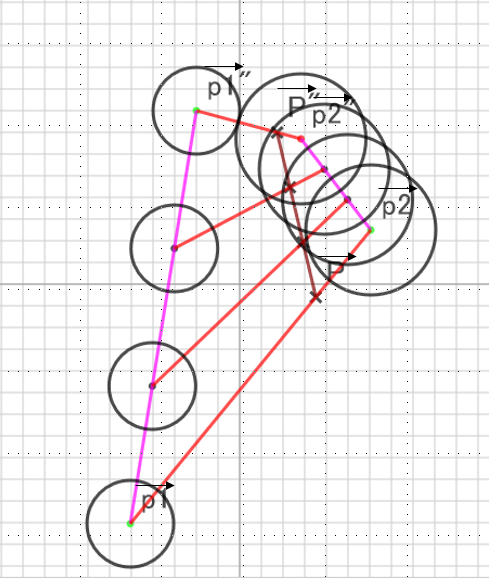
例を示すと以下のとおりである。二つのボールがビリヤード台の中で以下のように移動していたとする。なお、図で茶色い線は重心の移動を示す。

図で\({\vec {p_1}}\),\({\vec {p"_1}}\)と\({\vec {p_2}}\),\({\vec {p"_2}}\)は二つのボールの軌跡である。\(t_0\)の時は、二つのボールは\({\vec {p_1}}\),\({\vec {p_2}}\)に位置する。また、\(t_0 + dt'\)の時、二つのボールは衝突し\({\vec {p"_1}}\),\({\vec {p"_2}}\)に位置する。
ここで、次の計算時間\(t_1=t_0 + dt\)でのボールの位置を知りたい。但し、\( dt' < dt \)とする。即ち、現在の計算時間\(t_0\)と次の計算時間\(t_1\)の間に衝突が生じていたとする。
衝突後のボールの位置をビリヤード台座標系から直接求めようとすると複雑になるので、重心座標系を用いることとする。先の方程式から、重心座標系では、それぞれのボールの速さは衝突した後でも変化しない。また、二つのボールの速度は、「二つのボールの交点での接線に」平行な線に対して、光のように反射することも分かっている。
そこで、先のビリヤード台でのボールの動きに対して、重心座標系での動きを示すと以下の図のようになる。ここで、ビリヤード台座標系での\({\vec {p_1}}\),\({\vec {p"_1}}\)と\({\vec {p_2}}\),\({\vec {p"_2}}\)は、重心座標系では\({\vec {q_1}}\),\({\vec {q"_1}}\)と\({\vec {q_2}}\),\({\vec {q"_2}}\)である。なお、この図では、次の計算時間ではボールは平行な線に反射した線上のある地点になるので、適当に選んで示した。それらが、\({\vec {q'_1}}\),\({\vec {q'_2}}\)である。

この図から分かるように、重心座標系では、二つのボールは、二つの平行線の上をお互いに向き合うように移動し、衝突した後では、反射した平行線に沿ってお互いに離れていくように移動する。
別の例を示す。最初はビリヤード台座標系での移動を示す。また、図で茶色い線は重心の移動を示す。

これを重心座標系で表すと

この図で、3本の黒い線があるが真ん中の黒い線が二つのボールが衝突したときの交点での接線である。残りの二つは、ボールが跳ね返るときのその中心点に平行移動した接線である。それぞれのボールは、それぞれの平行移動した接線に対して反射するように中心点が移動する。
もう一つ例を示す。ビリアード台でのボールの動きは以下のとおりである。
先の動きとよく似ているが、重心座標系でのボールの動きは次のようになる。

ここで、時間\(t_1=t_0 + dt\)でのボールの位置を知るためには、反射した後のボールが辿る軌跡の角度を求める必要がある。今、衝突前のボールが辿る軌跡の傾きを\(\theta\)、ボールが衝突したときの衝突点での接線の傾きを\(\varphi\)とすると、図に示すように、衝突後のボールが辿る軌跡の傾きは、\(2 \varphi - \theta\)である。
ビリヤード台での座標系と重心系での座標系での関係を見ていくのは楽しいが、そろそろ、先を急ぐこととする。
次の記事では、これらの関係を使って、(衝突した後の)時間\(t_1=t_0 + dt\)でのボールの位置を計算する。