ボールの衝突をFunctional Reactive Programmingで表現する（８）

９．壁でも跳ね返る二つのボール

９．１　プログラムの実行

完成したプログラムの実行結果を最初に見る。なかなか面白い動きをしていることが分かる。

９．２　壁で跳ね返った時の位置

前回の記事で一直線上を走る二つのボールの衝突についてのプログラムが完成した。今度は、両側に壁があり、二つのボールはお互いに正面衝突したり、追突したりするだけでなく、壁でも跳ね返るようにする。壁での跳ね返りの係数は1とする。即ち、壁にぶつかったときは、同じ速さだが反対方向の速度で跳ね返ってくる。

例によって、現時点\(t\)の後、\(dt\)間経過するまでに壁にぶつかったとし、次の時点\(t+dt\)でのボールの位置を求める。左側に衝突した場合と、右側にした場合では、少し異なるが、図で示すと次のようになる。

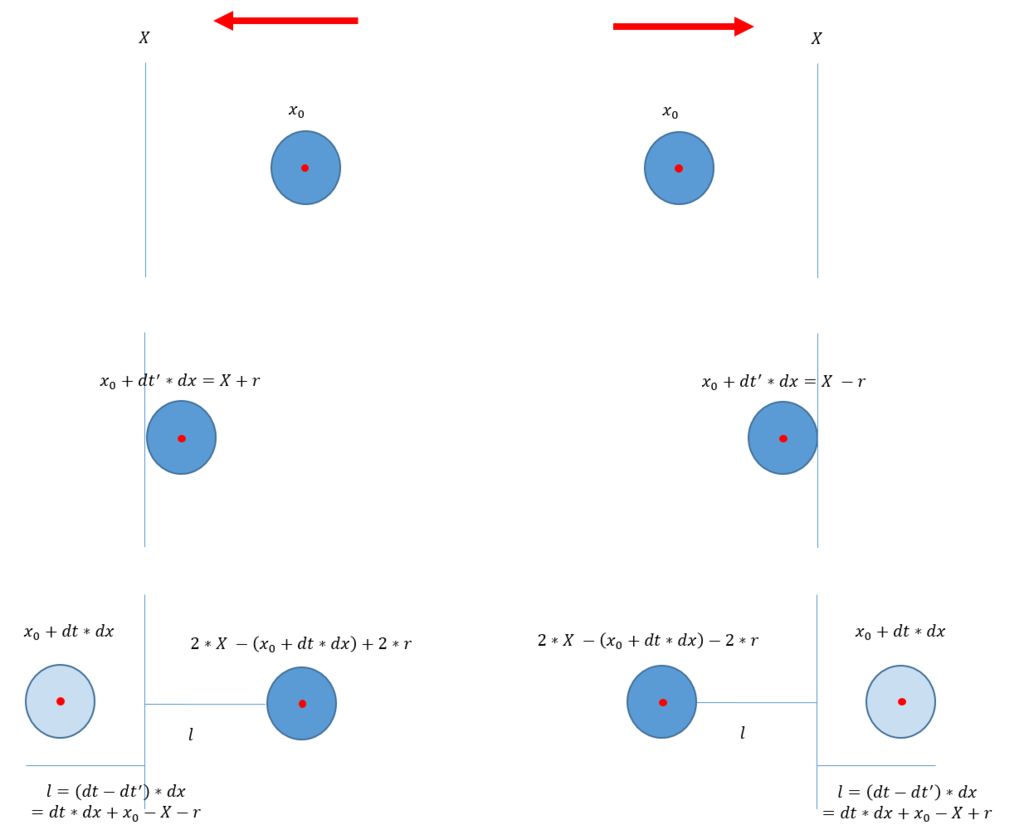
壁の位置を\(X\)、ボールの現在の位置を\(x_0\)、速度を\(dx\)、半径を\(r\)とした時、\(dt\)間経過するまでに衝突したとする。次の時点\(t_0+dt\)での位置は、左側に衝突していれば\(2 \times X -(x_0 + dt \times dx) + 2 \times r\)となり、右側では\(2 \times X -(x_0 + dt \times dx) - 2 \times r\)となる。

９．３　壁からの跳ね返りを実装する

衝突を示すデータ型のCollisionに、ボール同士の衝突に加えて、壁との衝突を加えることにする。最後の二つが壁に衝突したことを示すブール値であるが、最初の方は最初のボールが、二番目の方は二番目のボールが壁に衝突したかどうかを示すブール値である。ここでは、どちらの壁に当たったかは示さない。

data Collision = Collision Bool Ball Ball Bool Bool deriving (Eq, Show, Read)

衝突を調べるためのWireであるcollisionには、それぞれのボールが壁に衝突したかどうかを示す記述を追加する。これは次のようになる。

collision :: (HasTime t s) => Wire s () IO (Ball, Ball) Collision
collision = proc (b1@(Ball name1 r1 (V2 vx1 vy1) (V2 x1 y1) (V2 dt1 dt1')), b2@(Ball name2 r2 (V2 vx2 vy2) (V2 x2 y2) (V2 dt2 dt2'))) -> do
    let nx1 = x1 + vx1 * dt1
        nx2 = x2 + vx2 * dt2
        h1  = nx1 - r1 < (- wall) || nx1 + r1 > wall
        h2  = nx2 - r2 < (- wall) || nx2 + r2 > wall
        makeCollision :: Bool -> Ball -> Ball -> Bool -> Bool -> Collision
        makeCollision b b1 b2 h1 h2 = Collision b b1 b2 h1 h2 
    if abs (nx1 - nx2) > r1 + r2 
      then returnA -< makeCollision False b1 b2 h1 h2
      else returnA -< makeCollision True  b1 b2 h1 h2

上のプログラムで、 h1 = nx1 - r1 < (- wall) || nx1 + r1 > wallは、最初のボールが壁に衝突するかどうかを判定する。h2の方は二番目に対してである。

collisionからのデータを受けて次の位置と速度を与えなければならないが、まず位置の方は、衝突が左側で起きた場合は半径の2倍を加算し、右側で起きた場合は減算することに注意して、次のように変更する。

position :: (HasTime t s, Monad m) => (V2 Double) -> Wire s () m (V2 Double, String, Collision) (V2 Double, V2 Double)
position pInit = integralWith' collide' pInit
  where 
    collide' self (Collision b (Ball n1 r1 (V2 vx1 vy1) (V2 x1 y1) (V2 dt1 dt1')) (Ball n2 r2 (V2 vx2 vy2) (V2 x2 y2) (V2 dt2 dt2')) h1 h2) pos
            | h1 && self == n1 = if vx1 > 0 then V2 (2*wall - (x1+dt1*vx1) - 2 * r1) y1 else V2 (2*(-wall) - (x1+dt1*vx1) + 2 * r1) y1
            | h2 && self == n2 = if vx2 > 0 then V2 (2*wall - (x2+dt2*vx2) - 2 * r2) y2 else V2 (2*(-wall) - (x2+dt2*vx2) + 2 * r2) y2 
            | b  && self == n1 = if x1 > x2 then V2 (x2 + (r1 + r2)) y2 else V2 (x2 - (r1 + r2)) y2
            | b                = if x2 > x1 then V2 (x1 + (r1 + r2)) y1 else V2 (x1 - (r1 + r2)) y1
            | otherwise        = pos

速度の方は、壁に衝突したとき向きが逆になるだけなので、velocityにこれを加える。

velocity :: (HasTime t s, Monad m) => (V2 Double) ->  Wire s () m (String, Collision) (V2 Double) 
velocity vInit = constWith collide vInit
  where
    collide (self, (Collision b (Ball n1 r1 (V2 vx1 vy1) (V2 x1 y1) (V2 dt1 dt1')) (Ball n2 r2 (V2 vx2 vy2) (V2 x2 y2) (V2 dt2 dt2')) h1 h2))
            | h1 && self == n1  = V2 (-vx1) vy1
            | h2 && self == n2  = V2 (-vx2) vy2
            | b && self == n1   = V2 vx2 vy2
            | b                 = V2 vx1 vy1
            | self == n1        = V2 vx1 vy1
            | otherwise         = V2 vx2 vy2

constWith :: (Fractional a, HasTime t s)=> (w -> a) -> a -> Wire s e m w a
constWith correct = loop
  where
    loop x' = mkPure $ \ds w ->
      let dt = realToFrac (dtime ds)
          x  = correct w
      in x' `seq` (Right x', loop x)

９．４　プログラム全体

メインプログラムには壁の描写を加える。

{-# LANGUAGE Arrows #-}
-- module Main where

import Prelude hiding ((.),)
import Control.Wire
import Control.Monad.IO.Class
import FRP.Netwire
import Graphics.Rendering.OpenGL 
import Graphics.UI.GLFW 
import Data.IORef
import Linear.V2

import Ball
import Configure
import Collision

type Point = (Double, Double)
type Polygon = [Point]

renderPoint :: Point -> IO () 
renderPoint (x, y) = vertex $ Vertex2 (realToFrac x :: GLfloat) (realToFrac y :: GLfloat)

generatePointsForBall :: Ball -> Polygon 
generatePointsForBall (Ball name r (V2 vx vy) (V2 x y) (V2 dt dt')) = 
  map (\t -> (x+r*cos (t), y+r*sin (t))) [0,0.2..(2*pi)]

generatePointsForLeftWall :: Polygon 
generatePointsForLeftWall = 
  [ (-1, -1) 
  , (- wall, -1) 
  , (- wall, 1) 
  , (-1, 1) ] 

generatePointsForRightWall :: Polygon 
generatePointsForRightWall = 
  [ (1, 1) 
  , (wall, 1) 
  , (wall, -1) 
  , (1, -1) ] 

runNetwork :: (HasTime t s) => IORef Bool -> Session IO s -> Wire s e IO a (Ball, Ball) -> IO () 
runNetwork closedRef session wire = do 
  pollEvents 
  let color3f r g b = color $ Color3 r g (b :: GLfloat)
  closed <- readIORef closedRef 
  if closed 
    then return () 
    else do
      (st , session') <- stepSession session 
      (wt', wire' ) <- stepWire wire st $ Right undefined 
      case wt' of 
        Left _ -> return () 
        Right (b1,b2) -> do
          clear [ColorBuffer] 
          color3f 1.0 0.8 0.6
          renderPrimitive Polygon $ 
            mapM_ renderPoint $ generatePointsForBall b1
          color3f 0.8 0.2 0.2
          renderPrimitive Polygon $ 
            mapM_ renderPoint $ generatePointsForBall b2

          color3f 0.7 0.7 0.7
          renderPrimitive Polygon $ 
            mapM_ renderPoint $ generatePointsForLeftWall
          renderPrimitive Polygon $ 
            mapM_ renderPoint $ generatePointsForRightWall
          swapBuffers 
          runNetwork closedRef session' wire' 

simulation :: HasTime t s => Wire s () IO a (Ball, Ball)
simulation = proc _ -> do
    rec b1 <- ball "ball1" radius vInit1 pInit1 -< ("ball1", c)
        b2 <- ball "ball2" radius vInit2 pInit2 -< ("ball2", c)
        c <- collision -< (b1, b2) 
    returnA -< (b1, b2)

main :: IO () 
main = do
  initialize 
  openWindow (Size 640 640) [DisplayRGBBits 8 8 8, DisplayAlphaBits 8, DisplayDepthBits 24] Window
  closedRef <- newIORef False 
  windowCloseCallback $= do 
    writeIORef closedRef True 
    return True 
  runNetwork closedRef clockSession_ simulation
  closeWindow

ボールに関するプログラムは次のようになる。

{-# LANGUAGE Arrows #-}
module Ball (ball) where

import Prelude hiding ((.),)
import Control.Wire
import FRP.Netwire.Move
import Linear.V2
import Configure
import Collision

velocity :: (HasTime t s, Monad m) => (V2 Double) ->  Wire s () m (String, Collision) (V2 Double) 
velocity vInit = constWith collide vInit
  where
    collide (self, (Collision b (Ball n1 r1 (V2 vx1 vy1) (V2 x1 y1) (V2 dt1 dt1')) (Ball n2 r2 (V2 vx2 vy2) (V2 x2 y2) (V2 dt2 dt2')) h1 h2))
            | h1 && self == n1  = V2 (-vx1) vy1
            | h2 && self == n2  = V2 (-vx2) vy2
            | b && self == n1   = V2 vx2 vy2
            | b                 = V2 vx1 vy1
            | self == n1        = V2 vx1 vy1
            | otherwise         = V2 vx2 vy2

constWith :: (Fractional a, HasTime t s)=> (w -> a) -> a -> Wire s e m w a
constWith correct = loop
  where
    loop x' = mkPure $ \ds w ->
      let dt = realToFrac (dtime ds)
          x  = correct w
      in x' `seq` (Right x', loop x)


position :: (HasTime t s, Monad m) => (V2 Double) -> Wire s () m (V2 Double, String, Collision) (V2 Double, V2 Double)
position pInit = integralWith' collide' pInit
  where 
    collide' self (Collision b (Ball n1 r1 (V2 vx1 vy1) (V2 x1 y1) (V2 dt1 dt1')) (Ball n2 r2 (V2 vx2 vy2) (V2 x2 y2) (V2 dt2 dt2')) h1 h2) pos
            | h1 && self == n1 = if vx1 > 0 then V2 (2*wall - (x1+dt1*vx1) - 2 * r1) y1 else V2 (2*(-wall) - (x1+dt1*vx1) + 2 * r1) y1
            | h2 && self == n2 = if vx2 > 0 then V2 (2*wall - (x2+dt2*vx2) - 2 * r2) y2 else V2 (2*(-wall) - (x2+dt2*vx2) + 2 * r2) y2 
            | b  && self == n1 = if x1 > x2 then V2 (x2 + (r1 + r2)) y2 else V2 (x2 - (r1 + r2)) y2
            | b                = if x2 > x1 then V2 (x1 + (r1 + r2)) y1 else V2 (x1 - (r1 + r2)) y1
            | otherwise        = pos

integralWith' :: (Fractional a, HasTime t s) => (b -> w -> a ->  a) -> a -> Wire s e m (a, b, w) (a, a)
integralWith' correct = loop
  where
    loop x' = mkPure $ \ds (vel, n, c) ->
      let dt = realToFrac (dtime ds)
          x  = correct n c (x' + dt*vel)
      in x' `seq` (Right (x', dt), loop x)


ball :: (HasTime t s) => String -> Double -> (V2 Double) -> (V2 Double) -> Wire s () IO (String, Collision) Ball
ball name r v0 p0 = proc (self, collision) -> do
    vel <- velocity v0 -< (self, collision)
    (pos, dt) <- position p0 -< (vel, self, collision)
    returnA -< makeBall name vel pos dt
  where makeBall :: String -> V2 Double -> V2 Double -> V2 Double -> Ball
        makeBall n v p dt = Ball n r v p dt

衝突に関するプログラムは次のようになる。

{-# LANGUAGE Arrows #-}
module Collision (collision) where

import Prelude hiding ((.),)
import Control.Wire
import Control.Monad.IO.Class()
import FRP.Netwire()
import Linear.V2
import Configure


collision :: (HasTime t s) => Wire s () IO (Ball, Ball) Collision
collision = proc (b1@(Ball name1 r1 (V2 vx1 vy1) (V2 x1 y1) (V2 dt1 dt1')), b2@(Ball name2 r2 (V2 vx2 vy2) (V2 x2 y2) (V2 dt2 dt2'))) -> do
    let nx1 = x1 + vx1 * dt1
        nx2 = x2 + vx2 * dt2
        h1  = nx1 - r1 < (- wall) || nx1 + r1 > wall
        h2  = nx2 - r2 < (- wall) || nx2 + r2 > wall
        makeCollision :: Bool -> Ball -> Ball -> Bool -> Bool -> Collision
        makeCollision b b1 b2 h1 h2 = Collision b b1 b2 h1 h2 
    if abs (nx1 - nx2) > r1 + r2 
      then returnA -< makeCollision False b1 b2 h1 h2
      else returnA -< makeCollision True  b1 b2 h1 h2

データ型は初期値に関するプログラムは次のようになる。なお、データ型が複雑になってきたので、レコード構文に変更する。

{-# LANGUAGE Arrows #-}
module Configure where

import Linear.V2

-- one unit is equal to 10 meters
data Ball = Ball {name :: String,  semidiameter :: Double, speed :: V2 Double, location :: V2 Double, interval :: V2 Double } deriving (Eq, Show, Read)


radius :: Double
radius = 0.05

{-
pInit1 :: V2 Double
pInit1 = V2 (-0.5) 0

vInit1 :: V2 Double
vInit1 = V2 0.1 0

pInit2 :: V2 Double
pInit2 = V2 (-0.75) 0

vInit2 :: V2 Double
vInit2 = V2 0.2 0
-}

pInit1 :: V2 Double
pInit1 = V2 (0.5) 0

vInit1 :: V2 Double
vInit1 = V2 (-0.3) 0

pInit2 :: V2 Double
pInit2 = V2 (0.75) 0

vInit2 :: V2 Double
vInit2 = V2 (-0.4) 0

{-
pInit1 :: V2 Double
pInit1 = V2 (-0.75) 0

vInit1 :: V2 Double
vInit1 = V2 0.2 0

pInit2 :: V2 Double
pInit2 = V2 0.75 0

vInit2 :: V2 Double
vInit2 = V2 (-0.1) 0
-}

data Collision = Collision {colliding :: Bool, ball1 :: Ball, ball2 :: Ball, hitting1 :: Bool, hitting2 :: Bool} deriving (Eq, Show, Read)

wall = 0.9

９．５　やり残したこと

ボール同士の衝突と壁への衝突が同時に発生したときの処理はまだ含まれていない。