1.カリー化
前々回の記事でカリー化について触れたが、ここでは、もう少し詳しくカリー化について説明する。カリー化は、複数の引数をとる関数を一つの引数をとる関数に変換するものである。カリー化を具体的にイメージできるようにするために、例で説明する。
男女それぞれのグループがあり、それぞれのカップルについて、うまくいく場合とそうはいかない場合(好きか嫌い)を考え、それぞれの組合せについて関数で示すことを考えた。
2.集合から集合への写像
具体的に考えるために男性も女性もともに二人ずつであったとし、男性の集まりを\(X = \{jack, tom\}\)、 女性の集まりを\(A = \{ann, beth\}\)とし、相性の集まりを\(B = \{like, hate\}\)とする。男女ともに二人ずつであるので、可能なカップルの数は4である。また、それぞれのカップルが\(like\)か\( hate\)に割り当てられるため、可能な関数の数は\(2^4=16\)通りである。そこで、これらの関数のうちの三つ\(f,g,h\)を示したのが、次の図である。
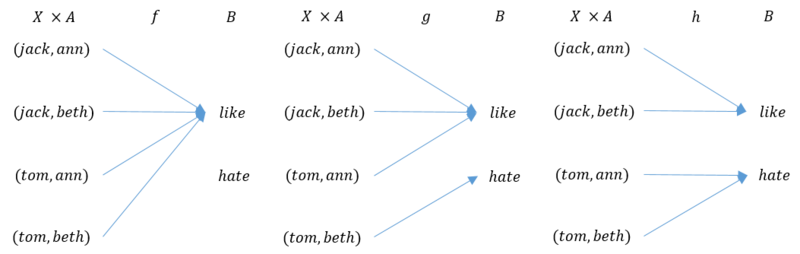
ここで、\(f\)はどのようなカップルでも相性が良いことを示している。また、\(g\)は\(tom\)と\(beth\)のカップルを除けば相性がよいことを示している。\(h\)は\(jack\)はだれとでも相性はよいが、\(tom\)はだれとも相性が良くないことを示している。
上記は、カップルの集合から相性の集合への写像となっているが、これを圏で示すと次のようになる。
(1) 対象
男性、女性、相性の集まりである\(X,A,B\)の三つである。
(2) 射
カップルを相性に写像する16個の関数\(f,g,h,...\)と後で説明する二つの恒等射\(id_{X \times A },id_B\)である。
(3) ドメインとコドメイン
次のようになっている。
\begin{eqnarray*}
f,g,h,... & : & X \times A \rightarrow B \\
id_{X \times A} & : & X \times A \rightarrow X \times A \\
id_B & : & B \rightarrow B
\end{eqnarray*}
(4) 恒等射
それぞれのカップルをそれ自身に移す\(id_{X \times A}\)とそれぞれの相性をそれ自身に移す\(id_B\)である。
(5) 合成
\(id_{X \times A}\)から\(f,g,h,...\)へ、\(f,g,h,...\)から\(id_B\)へ(他に、同一の恒等射)の 合成でき、両方とも\(f,g,h,...\)となる。
3.集合から写像への写像
集合から集合への写像はこれまで学んできた数学においてはごく自然なことであるが、次は、集合から写像の集合へ写像することで、解を見つける。最初に写像の集合から話をする。
少し、違和感を覚えるかもしれないが、女性の集まりから相性の集まりへの写像を考える。この時、双方とも2であるので、可能な写像の数は次に示すように\(2^2=4\)通りとなる。
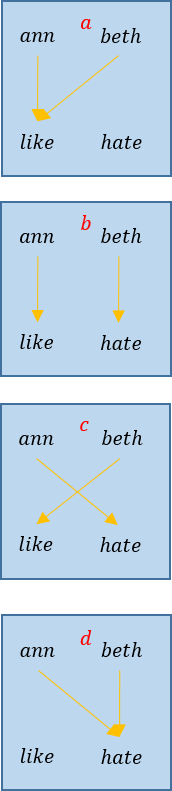
上記は写像の集まりであるが、これを対象とみなすことにする。圏ではこのような対象を指数対象と呼び、写像のドメインを\(A\)、コドメインを\(B\)とした時、指数対象は\(B^A\)と表す。これは、対象の大きさが、\(B\)(の大きさ)の\(A\)(の大きさ)乗となることを表していると考えればよい。上記の図のように、それぞれの写像を\(a,b,c,d\)で表すと、この図の指数対象は\(B^A=\{a,b,c,d\}\)となる。
さて、男性の集まりからこの指数対象への写像を考える。男性の人数が2であり、指数対象での写像の数が4であるので、可能な写像は、\(4^2=16\)通りである。以下の図ではその中の三つを示した。

\(\tilde{f}\)は、男性二人共を\(a\)(女性二人ともを\(like\)へ写像)へ写像した関数である。従って、\(\tilde{f}\)は2章での\(f\)と同じ結果を与える。同様に、\(\tilde{g}\)と\(g\)、\(\tilde{h}\)と\(h\)は同じ結果を与える。それでは、これに対する圏を考える。
(1) 対象
男性の集まり\(X\)と、女性の集まりから相性の集まりへの写像の集合(指数対象)\(B^A\)の二つである。
(2) 射
男性の集まりから指数対象へ写像する16個の関数\(\tilde{f},\tilde{g},\tilde{h},...\)と二つの恒等射\(id_{X},id_{B^A}\)である。
(3) ドメインとコドメイン
次のようになっている。
\begin{eqnarray*}
\tilde{f},\tilde{g},\tilde{h},... & : & X \rightarrow B^A \\
id_{X} & : & X \rightarrow X \\
id_{B^A} & : & {B^A} \rightarrow {B^A}
\end{eqnarray*}
(4) 恒等射
それぞれの男性をそれ自身に移す\(id_X\)とそれぞれの指数対象をそれ自身に移す\(id_{B^A}\)である。
(5) 合成
\(id_X\)から\(\tilde{f},\tilde{g},\tilde{h},...\)へ、\(\tilde{f},\tilde{g},\tilde{h},...\)から\(B^A\)へ(他に、同一の恒等射)合成でき、両方とも\(\tilde{f},\tilde{g},\tilde{h},...\)となる。
4.Haskellでの例
Haskellでは、カリー化する関数としてcurryを、カリー化した関数を元に戻す関数としてuncurryを用意している。
関数fstは対のデータを受けて最初のデータを返す関数である。型シグネチャを見ると次のようになっている。
Prelude> :t fst fst :: (a, b) -> a
実行例を示すと
Prelude> fst ("string", 4.5) "string"
Haskellのカリー化は次のように定義されている。
Prelude> :t curry curry :: ((a, b) -> c) -> a -> b -> c
これを用いて、fstをカリー化すると次のようになる。
Prelude> curry fst "string" 4.5 "string"
上記で、curry fst "string"がカリー化された関数で、 4.5はカリー化された関数への入力である。
実際、次のようになっている。
Prelude> :t curry fst "string" curry fst "string" :: b -> [Char]
上の関数は、一つの入力bを求めていることが分かる。
次に、式を定義して同じようなことを試みる。まず、2引数を受け取るcircleという関数を次のように定義する。
Prelude> let circle = \ (x,y) -> x*x + y*y
これを実行する。
Prelude> circle (3,4) 25
カリー化する。
Prelude> let curryCircle = curry circle
実行してみる(以下では、curryCircle 3までを関数とみる)。
Prelude> curryCircle 3 4 25
最後にuncurryを用いてカリー化されたものを対にする。
Prelude> uncurry min (4, 5) 4
minのもともとの使い方は以下のようになっていた。
Prelude> min 4 5 4