1.写像
圏論では射が重要な概念を担っているが、射の中核をなすのは写像である。ここでは、写像について詳しく調べることとする。
集合\(A,B\)間の写像\(f\)は、任意の\(a \in A\)に対してある\(b \in B\)を必ず対応付けるものであり、\(f: A \rightarrow B\)で表す。また、\(f(a)=b, a \in A, b \in B\)とも表す。
また、全ての\(b \in B\)に対して、\(f(a)=b\)となる\(a\)が存在するとき、この写像を全射という。また、任意の\(a,a’ \in A\)に対して、\(a \neq a’ \)の時、\(f(a) \neq (a’) \)であれば、この写像を単射という。
例として集合\(A=\{a,b,c\}\)と集合\(B=\{1,2\}\)があったとする。この時、考えられる写像を図で表すと、次の8個となる。これらにおいて、最初と最後を除いて、残りの写像は全射である。単射の写像は、ここには存在しない。

集合\(A=\{a,b,c\}\)から集合\(B=\{1,2,..,n\}\)への全ての写像を求めるプログラムをHaskellで作成すると次のようになる。
mapping3 n = [(('a', x),('b', y),('c', z)) | x <- [1..n], y <- [1..n], z <- [1..n]]
実行してみる。
Prelude> :load "Mapping.hs" [1 of 1] Compiling Mapping ( Mapping.hs, interpreted ) Ok, modules loaded: Mapping. *Mapping> mapping3 2 [(('a',1),('b',1),('c',1)),(('a',1),('b',1),('c',2)),(('a',1),('b',2),('c',1)),(('a',1),('b',2),('c',2)),(('a',2),('b',1),('c',1)),(('a',2),('b',1),('c',2)),(('a',2),('b',2),('c',1)),(('a',2),('b',2),('c',2))]
\(B\)の要素数が3の場合を求めると、次のように27個の写像があることが分かる。例えば、( ('a',1),('b',2),('c',3) )の写像は、全射であるとともに単射でもある。
*Mapping> mapping3 3 [(('a',1),('b',1),('c',1)),(('a',1),('b',1),('c',2)),(('a',1),('b',1),('c',3)),(('a',1),('b',2),('c',1)),(('a',1),('b',2),('c',2)),(('a',1),('b',2),('c',3)),(('a',1),('b',3),('c',1)),(('a',1),('b',3),('c',2)),(('a',1),('b',3),('c',3)),(('a',2),('b',1),('c',1)),(('a',2),('b',1),('c',2)),(('a',2),('b',1),('c',3)),(('a',2),('b',2),('c',1)),(('a',2),('b',2),('c',2)),(('a',2),('b',2),('c',3)),(('a',2),('b',3),('c',1)),(('a',2),('b',3),('c',2)),(('a',2),('b',3),('c',3)),(('a',3),('b',1),('c',1)),(('a',3),('b',1),('c',2)),(('a',3),('b',1),('c',3)),(('a',3),('b',2),('c',1)),(('a',3),('b',2),('c',2)),(('a',3),('b',2),('c',3)),(('a',3),('b',3),('c',1)),(('a',3),('b',3),('c',2)),(('a',3),('b',3),('c',3))]
集合\(B\)は要素が1個だけであったとする。この時考えられる写像を同じように図で表すと、次の1個となる。このとき、この写像は全射である。
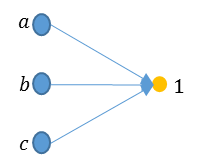
また、プログラムで調べると次のようになる。
*Mapping> mapping3 1 [(('a',1),('b',1),('c',1))]
また、圏論では、全ての対象を一つの対象に写像するような射が丁度一つ存在するとき、写像される側の対象を終対象という。上の図で、\(A\)の要素は全て\(B\)の要素1に写像されるので、圏論で考えれば(圏にした時に、\(B\)に恒等射が存在し、要素1から要素1への写像も存在するため)、この要素1は終対象となる。
最後に、集合\(B\)が空であった場合を考える。プログラムを実行すると、写像が存在しないことが分かる。
*Mapping> mapping3 0 []
2.写像を求めるプログラム
これまでの議論をもとに、有限な要素を持つ二つの集合\(A\)と\(B\)が与えられた時、可能な写像を全て列挙する関数をHaskellで実現することを考える。
ここでは、1対多の写像を中心に考えるのでまずそのような写像を図に示す。下図は1対3での写像である。写像の種類は3種類になる。
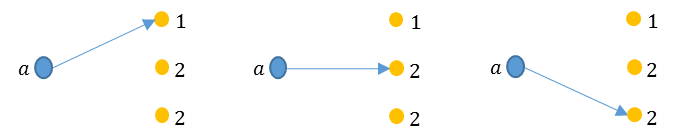
プログラムを考えるために、集合\(A=\{a,b,c\}\)から集合\(B=\{1,2\}\)への全ての写像をどのように求めたらよいかをもう一度考えてみる。要素\(\{c\}\)から、集合\(B=\{1,2\}\)への可能な写像は、\((c,1),(c,2)\)である。これを集合にしたものを\(mapping(c) = \{(c,1),(c,2)\}\)とする。同様に、要素\(\{b\}\)から、集合\(B=\{1,2\}\)への可能な写像の集合を\(mapping'(b) = \{(b,1),(b,2)\}\)とする。
要素\(\{b,c\}\)から、集合\(B=\{1,2\}\)への可能な写像の集合は、\(mapping'(b)\)と\(mapping(c)\)との直積、即ち、それぞれの要素同士の組合せの全て、
\begin{eqnarray*}
\{( (b,1),(c,1) ),( (b,1),(c,2) ), \\
( (b,2),(c,1) ),( (b,2),(c,2) ) )\}
\end{eqnarray*}
となる。
この集合を
\begin{eqnarray*}
mapping(b,c) & = \{ & ( (b,1),(c,1) ),( (b,1),(c,2) ), \\
&& ( (b,2),(c,1) ),( (b,2),(c,2) )\}
\end{eqnarray*}
とする。
同様に、要素\(\{a,b,c\}\)から、集合\(B=\{1,2\}\)への可能な写像の集合は、\(mapping'(a)\)と\(mapping(b,c)\)との直積となり、その集合は
\begin{eqnarray*}
mapping(a,b,c) & = \{ & ( (a,1),(b,1),(c,1) ),( (a,1),(b,1),(c,2) ), \\
&& ( (a,1),(b,2),(c,1) ),( (a,1),(b,2),(c,2) ), \\
&& ( (a,2),(b,1),(c,1) ),( (a,2),(b,1),(c,2) ), \\
&& ( (a,2),(b,2),(c,1) ),( (a,2),(b,2),(c,2) )\}
\end{eqnarray*}
そこで、\(mapping'\)と\(mapping\)をHaskellで実現することを考える。集合\(A\)も集合\(B\)もその要素はリストで表すことにする。即ち、\(A\)であればa=['a','b','c']のように表すこととする。また、\(B\)の要素も1と2だけではなく有限個の要素を自由に選べるようにする。
そこで、\(mapping'\)に対してはmapping' y n という関数を用意する。これは、要素yから集合(リスト)nへの写像の集合を表す(前の例でいえば、nは\(B=\{1,2\}\)をリストで表したもので、[1,2]となる)。なお、出力となる写像の集合もリストで表す。即ち、\(mapping'(b) = \{(b,1),(b,2)\}\)に対して以下のようになる。
*Mapping> mapping' 'b' [1,2] [('b',1),('b',2)]
\(mapping(a,b,c),mapping(b,c),mapping(c)\)はmapping m nとする。これは、集合mから集合nへの写像の集合とする。集合mは先ほどの例でいえば集合\(A=\{a,b,c\}\)の部分集合で、\(\{c\}\)であったり、\(\{b,c\}\)であったり、\(\{a,b,c\}\)であったりするが、これをリストとして表したものである。集合nは集合\(B=\{1,2\}\)をリストで表したものである。\(mapping(b,c)\)は\(mapping'(b)\)と\(mapping(c)\)の直積であるので、内包表記を用いて、Haskellでは次のように実現できる。
mapping ('b':['c']) [1,2] = [[x] ++ y | x <- (mapping' 'b' [1,2]), y <- (mapping ['c'] [1,2])]
mappingの関数において、写像する側の集合が空の時の、即ち、空リストの時の写像は空写像である。そこで、mapping [ ] _ = [[]]すると、mapping'とmappingは次のように定義できる。
module Mapping where mapping' :: a -> [b] -> [(a,b)] mapping' y n = map (\x -> (y,x)) n mapping :: [a] -> [b] -> [[(a,b)]] mapping [] _ = [[]] mapping (m:mx) n = [[x] ++ y | x <- (mapping' m n), y <- (mapping mx n)]
これを実行してみる。
*Mapping> mapping ['a'..'c'] [1,2] [[('a',1),('b',1),('c',1)],[('a',1),('b',1),('c',2)],[('a',1),('b',2),('c',1)],[('a',1),('b',2),('c',2)],[('a',2),('b',1),('c',1)],[('a',2),('b',1),('c',2)],[('a',2),('b',2),('c',1)],[('a',2),('b',2),('c',2)]] *Mapping> mapping ['a'..'c'] [1..3] [[('a',1),('b',1),('c',1)],[('a',1),('b',1),('c',2)],[('a',1),('b',1),('c',3)],[('a',1),('b',2),('c',1)],[('a',1),('b',2),('c',2)],[('a',1),('b',2),('c',3)],[('a',1),('b',3),('c',1)],[('a',1),('b',3),('c',2)],[('a',1),('b',3),('c',3)],[('a',2),('b',1),('c',1)],[('a',2),('b',1),('c',2)],[('a',2),('b',1),('c',3)],[('a',2),('b',2),('c',1)],[('a',2),('b',2),('c',2)],[('a',2),('b',2),('c',3)],[('a',2),('b',3),('c',1)],[('a',2),('b',3),('c',2)],[('a',2),('b',3),('c',3)],[('a',3),('b',1),('c',1)],[('a',3),('b',1),('c',2)],[('a',3),('b',1),('c',3)],[('a',3),('b',2),('c',1)],[('a',3),('b',2),('c',2)],[('a',3),('b',2),('c',3)],[('a',3),('b',3),('c',1)],[('a',3),('b',3),('c',2)],[('a',3),('b',3),('c',3)]] *Mapping> mapping ['a'..'c'] [1] [[('a',1),('b',1),('c',1)]] *Mapping> mapping ['a'..'c'] [] [] *Mapping> mapping [] [1..3] [[]]
最後の二つの実行例は写像される方が空の集合の場合と写像する方が空の集合の場合である。実行結果は、前者では写像は存在しないであり、後者では空写像が存在する、である。
圏論では一つの対象をすべての対象に写像するような射が丁度一つ存在するとき、写像する側の対象を始対象と呼ぶ。集合から集合への写像の場合、写像する側の集合が空である時、丁度一つの空写像によって、すべての対象に写像されるので、(これらの集合と写像で圏を構成すれば)この時の空集合は始対象となる。
例を挙げて終対象を考える。いま、集合を\(A=\{a,b,c\}\)とする。これを圏で表すと次のようになる。
(1)対象:集合\(A=\{a,b,c\}\)
(2)射:
(3)ドメインとコドメイン:
(4)恒等射:\(id_A : A \rightarrow A\)
(5)合成:(恒等射だけの合成)
何とも単純な圏だが、これに終対象を明示することにする。\(a\), \(b\), \(c\)のいずれもが終対象になりえるが、ここでは、\(a\)を終対象とする。この時の圏は下図のようになっている。
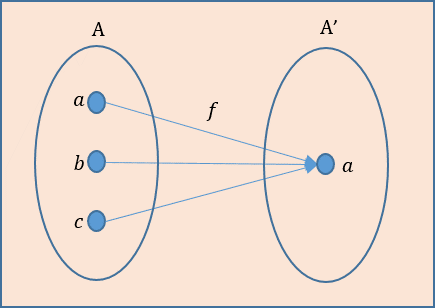
この圏は次のように構成される。
(1)対象:集合\(A=\{a,b,c\}\)と集合\(A'=\{a\}\)
(2)射:\(f\)
(3)ドメインとコドメイン:\(f:A \rightarrow A'\)
(4)恒等射:\(id_A : A \rightarrow A\), \(id_{A'} : A' \rightarrow A'\)
(5)合成:\(f\)と恒等射の合成
\(b\)も終対象となるので、先ほどの図にこれを加えると下図のようになる。

この図で、\(A"\)から\(A'\)への写像は\(f|A"\)であり、\(A'\)から\(A"\)への写像は\(g|A'\)である。ここで、\(f|A"\)は対象\(A\)で定義されている関数\(f\)をそれに含まれる対象\(A"\)の中で用いることを意味する。\(g|A'\)も同様である。
この時、
\begin{eqnarray*}
g|A' \circ f|A" & = & id_{A"} \\
f|A" \circ g|A & = & id_{A'}
\end{eqnarray*}
が成り立っている。
一般に、二つの集合\(A,B\)があり、これらの集合間での相互の写像\(f,g\)があった時、\(f \circ g = id\)かつ\(g \circ f = id\)の時、\(g = f^{-1}\)となり、\(f\)を同型写像(isomorphism)という。