6.4 Haskellで理解する
米田の補題の補題を下図の可換図式を用いて説明した。Haskellを用いてさらに理解を深めることとしよう。
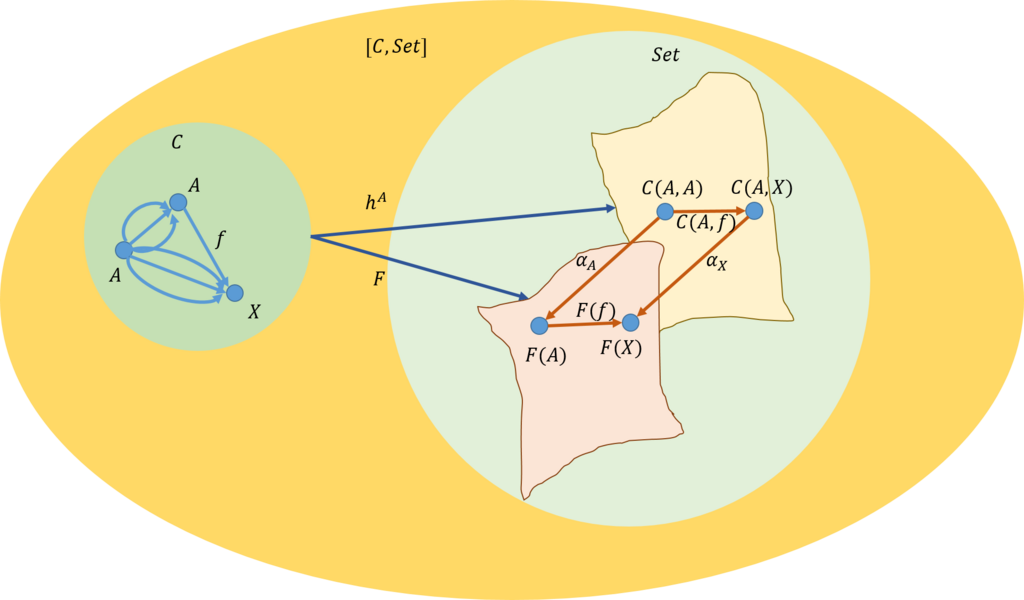
Bartosz Milewskiさんが上手に説明しているので、それを借りることにしよう。\({\rm Hom}\)関手を作成しよう。\(Reader\)のデータ型を定めよう。これは、射の集合だ。そこで、ドメインを型変数\(a\)で、コドメイン\(x\)とし、\(a\)から\(x\)への射の集まりと考えると、型構築子を\(Reader\)として、次のように定義できる。
type Reader a x = a -> x
\(Reader\)は関手なので、クラス\(Functor\)のインスタンスとするためには、次のようにする。
instance Functor (Reader a) where fmap f g = f . g
プログラムは下図を意味する。
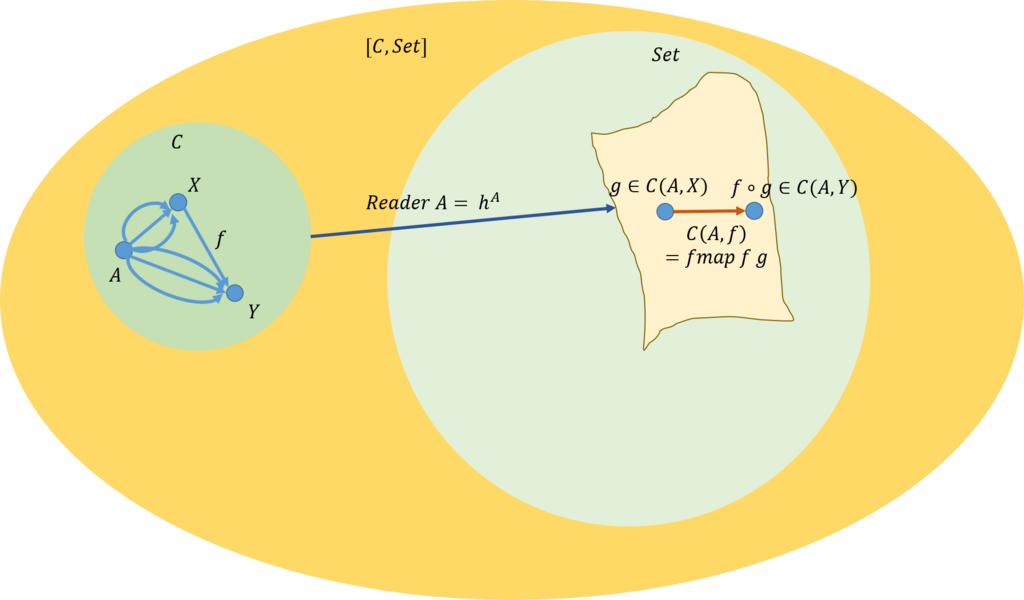
そして、自然変換\(\alpha\)は多相関数なので、次のように定義できる(ドメインやコドメインの方が型変数になっているものを多相関数という)。
alpha :: forall x . (a -> x) -> F
これは、以下の可換図式と同じである。

米田の補題は、
forall x . (a -> x) -> F ~= F a
と言っている。即ち、自然変換と\(F \ a\)の要素は一対一に対応すると言っている。
Haskellでは、右の項の\(F \ a\)は通常、データ型として扱う。そして、\(F\)は\(a\)を包んでいるコンテイナと考える。左の項は、引数として関数をとる、多相関数だ。米田の補題は、二つの項が同値だと言っている。即ち、同じ情報を有していると言っている。
言い方を変えると、
alpha :: forall x . (a -> x) -> F
という多相関数が与えられると、\(a\)のコンテイナ\(F\)を得ることができる。逆に、\(a\)のコンテイナ\(F\)が与えられる、先の多相関数を得ることができると言っている。
米田の補題の証明では、\(A\)から\(A\)への恒等射\(id\)を用いた。証明の手順を追っていこう。
\(id_A\)に対して、\(F (A)\)の任意の一つの要素\(p \in F(A)\)を対応させよう。即ち、
alpha id :: F a p :: F a
\(id_A\)を\(p\)に写す自然変換を\(\alpha\)とすると、下図の可換図式を得る。
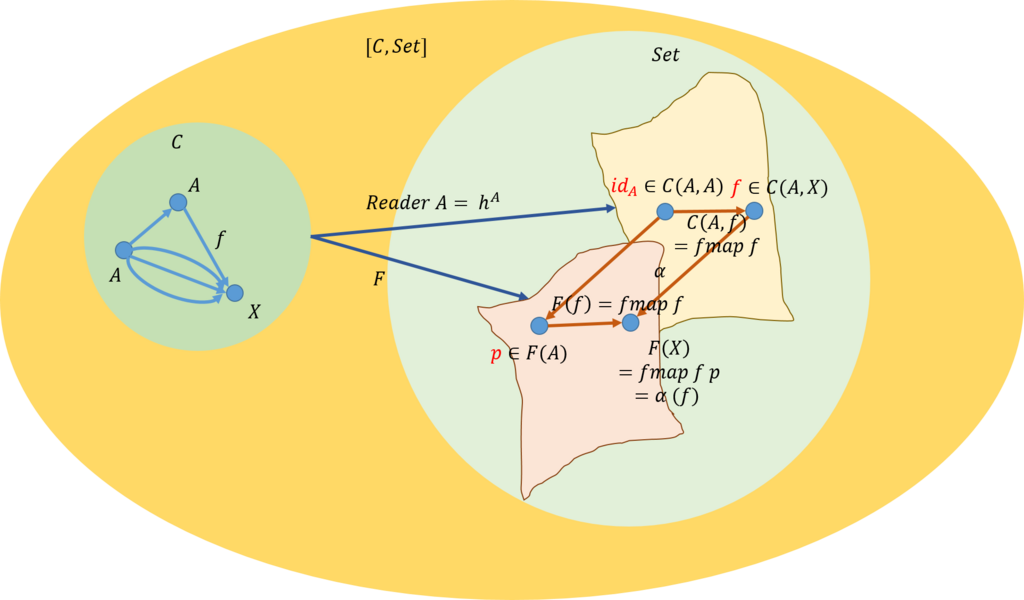
従って、
alpha f = fmap f p
を得る。
逆に、\(p\)を任意にするのではなく、\(f\)を任意にしてもよいことが分かる。これにより米田の補題が証明されたこととなる。
米田の補題の応用の一つは、継続渡しスタイル(continuation-passing style)のプログラムである。興味のある人は調べて欲しい。