7.5 随伴の解釈
随伴の定義は次のようになっていた。
二つの局所的に小さな圏\(\mathcal{C},\mathcal{D}\)において、関手の対\(R: \mathcal{C} \rightarrow \mathcal{D}, L: \mathcal{D} \rightarrow \mathcal{C}\)が三角恒等式を満たす次の射\(ϵ,η\)を有する時、随伴であるという。
\begin{eqnarray}
ϵ : L \circ R \rightarrow I_\mathcal{C} \\
η : I_\mathcal{D} \rightarrow R \circ L
\end{eqnarray}
この定義を理解することとしよう。随伴の趣旨は、二つの局所的に小さな圏があった時にそれが等しいということを定義することであった。そこで、一方の圏\(\mathcal{D}\)に、左随伴関手\(L\)を施した後で、右随伴関手\(R\)を施したときに、下図のように圏\(\mathcal{D}\)に戻ってくる。
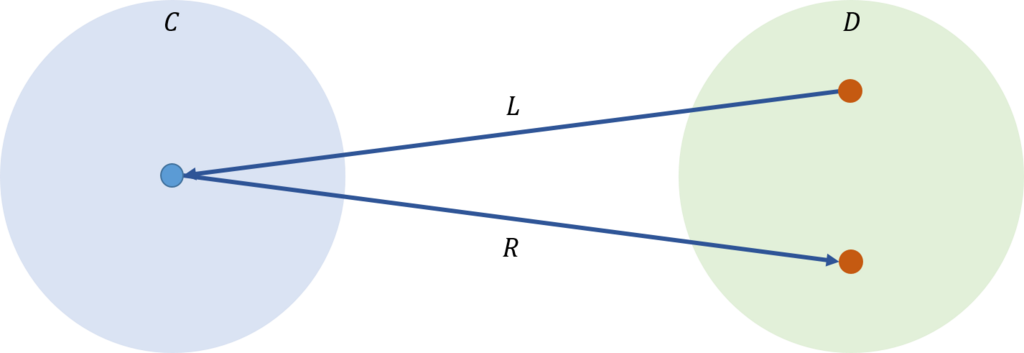
通常は等しいというときは、重なることが前提になっているが、圏論ではこれを緩めてある。関数\(η\)だけずれていても等しいということにしている。これを示すと下図のようになる。
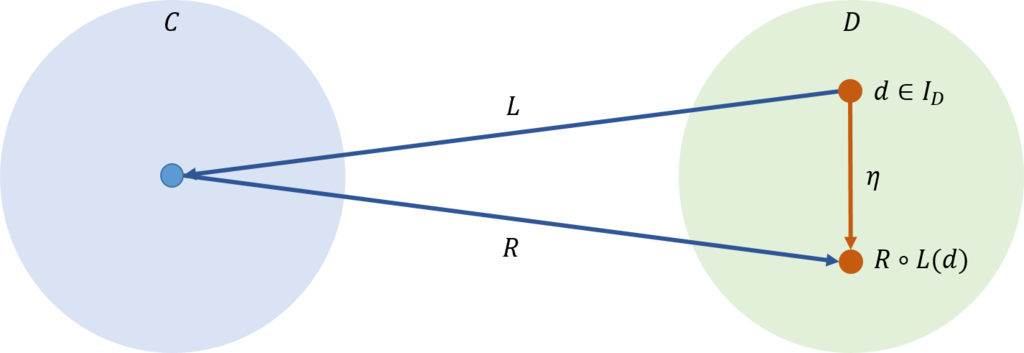
即ち、恒等射\(I_D\)の任意の要素を\(d\)とした時、これに\(R \circ L\)を施したとする。このとき、その移動後の場所は、同じところではなく、自然変換\(η: I_D \rightarrow R \circ L\)を行った先、即ち、\(R \circ L (d)\)となる。これが圏論での二つの圏が等しいと見なす定義の内容の一つだ。これまでの同型という言葉は使えないので、随伴という言葉を用いている。
この移動は、\(R \circ L \)というコンテナの中に\(d\)を納めるという気分だ。コンテナに入れただけなので同じと見なしてもよいだろうということだ。そして、モノイドでの\(return\)と同じだということも感覚的にわかると思う。

逆に、圏\(\mathcal{C}\)に、右随伴関手\(R\)を施した後で、左随伴関手\(L\)を施したときに、下図のように圏\(\mathcal{C}\)に戻ってくる場合について考えてみよう。
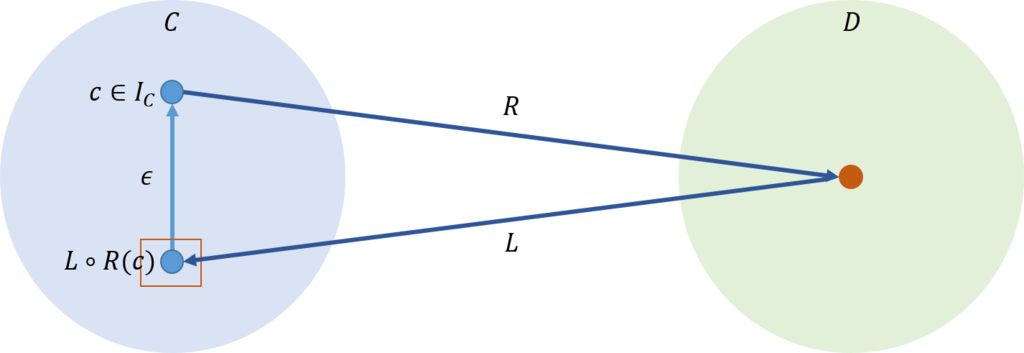
このときは、\(L \circ R \)というコンテナの中から前から入っていた\(c\)を取り出すという気分だ。コモノイドでの\(extract\)と同じだということがやはり感覚的にとらえることができ面白い。