2.コモナド
今回の記事はコモナド(余モンドとも言われる)だ。モナドはあちらこちらで出会うことが多いが、コモナドについての説明はそれほど多くない。今回の記事でも示すが、実はコモナドの概念はとても面白く、現実の世界の中でこれはコモナドではと思うことが多々ある。同窓会などで、久しぶりにかつてのクラスメイトに会って、昔話に話を咲かせているときに、思い出が違っていることにビックリすることが往々にしてある。事実は変わらないはずなのだが、年月がたつにつれてそれぞれの記憶が変容し、異なってしまったのだろう。これなどコモナドのよい例だと思うのだが、正しいかどうかは記事を読んでから確認して欲しい。
2.1 コモナドの定義
コモナドとモナドは双対概念だ。コモナドは、モナドを定義したときの射の矢印の方向を反対にするだけなのだが、その概念から受け取る感覚は、随分と異なるものになる。圏論でのモナドは哲学からの借用語だが、元々の意味は、単純な実体(elementary particle)であった。そしてそれを表現したものを、表象(representation)と呼んでいた。
これを利用して、圏論での基本的な概念は次のようになっている。
1)単純な実体\(A\)をカプセル化して表象\(T(A)\)を得るための
\begin{eqnarray}
return:A \rightarrow T(A)
\end{eqnarray}
と、
2)カプセル化したものをさらにカプセル化してもそれは変わらないとするための
\begin{eqnarray}
join:T(T(A)) \rightarrow T(A)
\end{eqnarray}
という射を導入して、モナドを定義した。
コモナドはこれとは反対の概念になるので、表象から単純な実体を得ることと、表象からさらに表象化されたものを作るということになる。圏論でコモナドを定義するときは、
1)カプセルをはずして対象を得る、即ち、
\begin{eqnarray}
extract:W(A) \rightarrow A
\end{eqnarray}
と、
2)カプセル化したものをさらにカプセル化する
\begin{eqnarray}
duplicate:W(A) \rightarrow W(W(A))
\end{eqnarray}
という射を導入すればよい。
2.2 コモナドはライフゲームに生かされている
それでは、コモナドはどのような場面に現れるのであろう。Bartosz Milewskiさんが動画の中で教えてくれたのがライフゲーム(Conway’s Game of Life)だ。ライフゲームを簡単に説明しよう。
ライフゲームは、1970年にイギリスの数学者ジョン・ホートン・コンウェイ(John Horton Conway)により生み出された。これは、生物集団の動的な変化の一端を示してくれるなかなか面白いシミュレーションゲームだ。集団内の各生物の生死はそれを取り囲む環境によって決まるという簡単なルールを導入しただけで、生物集団が消滅したり、成長したり、循環するなどのダイナミックな動きを示してくれる。ルールは次の4個だけだ。
誕生:死んでいるセルに隣接する生きたセルが丁度三つあれば、次の世代は誕生する。
生存:生きているセルに隣接するセルが二つか三つならば、次の世代は生存する。
過疎:生きているセルに隣接する生きたセルが一つ以下ならば、過疎により死滅する。
過密:生きているセルに隣接するセルが四つ以上ならば、過密により死滅する。
例を下図に示そう。
このルールから次のことが言える。中心のセルが、誕生してくるか、生き残るか、死滅するかは、その周りの8つのセルの状態によって定まる。次世代の中心のセルの状態\(A\)は、現世代での中心のセルを取り巻いている環境\(W(A)\)によって定まると考えることができる。即ち、\( W(A) \rightarrow A\)と考えることができる。
中心のセル\(A\)を取り巻く周辺のセルの状態\(W(A)\)は環境を与えたが、このときの周辺セルの状態\(W(A)\)から、これらのセルを取り巻く前世代の環境\( W ( W(A)\)へと(あるいはこれを作り出す候補の一つへと)立ち返ることができるであろう。これは、\( W(A) \rightarrow W(W(A))\)と考えることができるだろう。
このように考えると、ライフゲームはコモナドの概念に即したものと言える。ライフゲームで検索するとYouTubeにたくさんの例が載っているので、興味のある読者は参考にされるとよいと思う。
2.3 コモナドは信号処理でも生かされている
Bartosz Milewskiさんは、ライフゲームのほかにもう一つの例を挙げてくれた。それは信号処理だ。我々がコンサートホールで聴く音は、楽器の音そのものではない。直接伝わってくる音だけではなく、壁に跳ね返って入ってくる音もあるし、さらには壁で跳ね返った音が別の壁で跳ね返って入ってくる音もある。一般には、楽器から出た音がコンサートホールというフィルタを通った後の音を聴いていると考えてよい。
これを工学的に扱うのが信号処理だ。コンサートホールでのオーケストラと聴衆の関係をモデル化すると下図のようになる。オーケストラが出す音は入力信号で、聴衆が聞く音は出力信号だ。オーケストラの音はホールという音響装置を伝わって聴衆の耳に入るが、入力信号を変化させて異なる信号を出力するものをフィルタと呼ぶ。この例ではフィルタの役割をしているのはホールだ。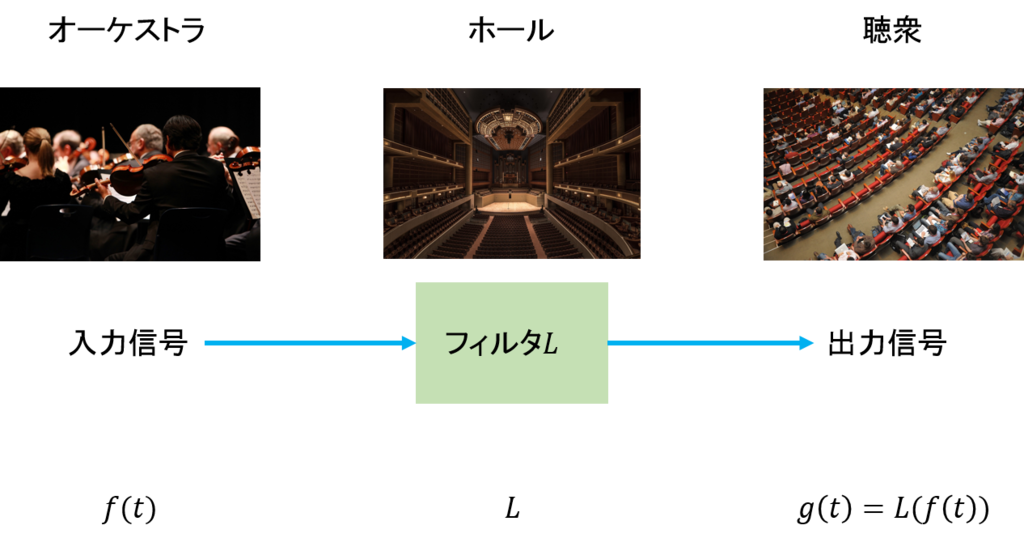
\begin{eqnarray}
L(C_1 f_1(t)+ C_2 f_2(t)) &=& C_1 L(f_1(t))+ C_2 L(f_2(t)) \\
L(f(t-τ)) &=& g(t-τ)
\end{eqnarray}
最初の式は線形であることを表している。すなわち入力信号が\(C_1 f_1(t)\)と\(C_2 f_2(t)\)とを加えたものであるとき、出力信号は、やはり、それぞれの出力信号\(C_1 L(f_1(t))\)と\(C_2 L(f_2(t))\)との和になるというものだ。最後の式は、時不変を表すもので、時間を変えて入力信号を与えたとしても、出力信号の形は同じになるというものだ。即ち、時間に依らないというものだ。
これらの条件を前提にして、入力信号に対する出力信号を得るためには、基本演算として畳み込みを利用する。これを用いるためにはインパルス応答を理解しておかないといけない。
インパルスは、時間幅が無限小で高さが無限大のパルスをいう(数学的なモデルなので、実感としてつかみにくいが、時間\(t=0\)のときだけ高さが1になる信号と理解しておけばよい)。このインパルスを入力信号としてフィルタに入力したとき、そこから出力された出力信号をインパルス応答という。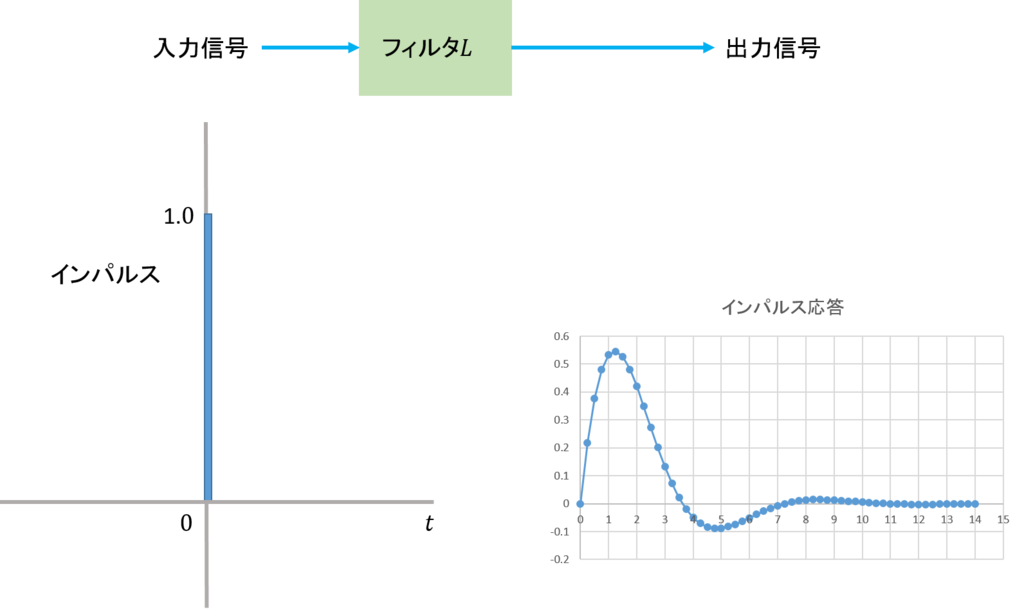

その原理を示したのが下図である。入力信号が始まるとき、即ち\(τ=0\)のときの出力信号を求める(橙色)。これは、入力信号の高さ分だけインパルス応答を高めてあげればよい。同じように、時不変であることを利用して、1単位時間だけ経過したときに受けた入力信号、即ち\(τ=1\)、のときの出力信号を求める(薄茶色)。同じように、\(τ=2,3,4…\)に対しても出力信号を求める(薄緑、肌色、茶…)。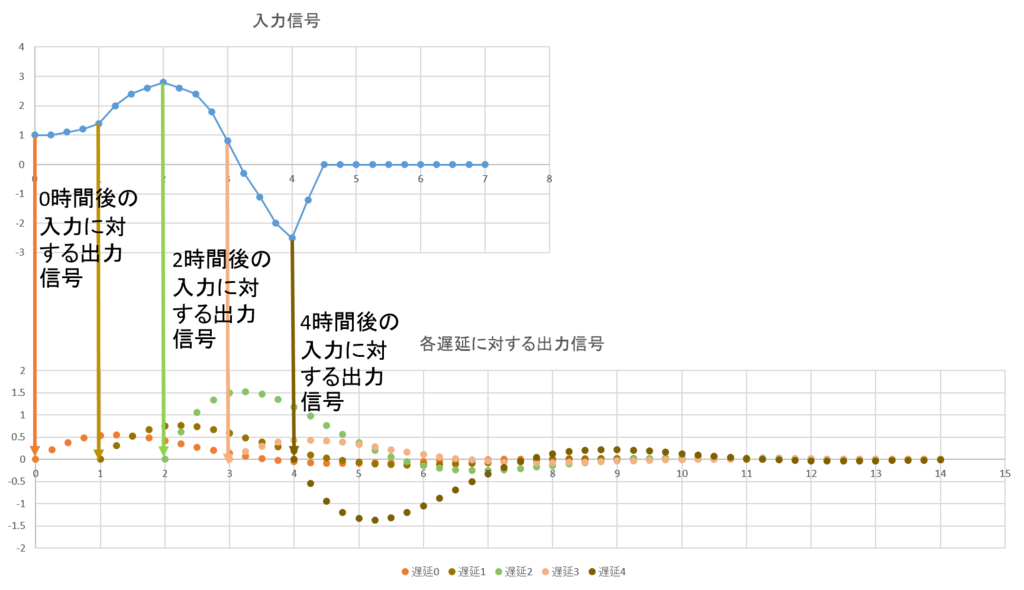
それでは、時間が\(m\)のときの出力信号がどのようになるかを考えてみよう。これは、線形であることを利用して、時間\(n\)(但し\(n \le m\))の出力の和となる。例えば、\(m=4\)であれば、\(n=0,1,2,3,4\)の出力信号の和となる。入力信号を\(f(t)\)としインパルス応答を\(h(t)\)として、式で表すと、
\begin{eqnarray}
g(m) = \sum^m_{n=0}f(n) h(m-n)
\end{eqnarray}
となる。ところで、\(f(n)\)は、時間\(n\)から\(n+1\)までを代表した値であるので、それを明示すると上の式は次のようになる。
\begin{eqnarray}
g(m) = \sum^m_{n=0}f(n) h(m-n) \times ( (n+1) –n)
\end{eqnarray}
そこで、刻み幅を1ではなく、微小な間隔\(dτ\)としよう。そして、\(m,n\)を\(mdτ,ndτ\)で置き換えると上式は、
\begin{eqnarray}
g(mdτ) = \sum^{mdτ}_{ndτ=0}f(ndτ) h(mdτ-ndτ) dτ
\end{eqnarray}
となる。さらに、\(t=mdτ, τ=ndτ\)とすると上式は、
\begin{eqnarray}
g(t) = \sum^t_{τ=0}f(τ) h(t -τ) dτ
\end{eqnarray}
\(h(t-τ)\)の値は、\(τ\)が\(-\infty\)から0までと、\(t\)から\(\infty\)まででは0であることに注意して、上式を積分の形にすると次の式が得られる。
\begin{eqnarray}
g(t) = \int^{-\infty}_{\infty}f(τ) h(t-τ)dτ
\end{eqnarray}
このように信号処理での畳み込みは、これまでに入力された信号毎に、その大きさに合わせてインパルス応答を求め、それらを重ね合わせたものである。このため、出力信号は、入力信号をフィルタ\(L\)によってカプセル化されたものと見なすことができる。もし入力信号も同じようにカプセル化されたものであるとするならば、\(g:L(A) \rightarrow L(L(A))\)となり、コモナドの\(duplicate\)を想起させる。これについては、後半でもう一度触れることにしよう。
2.4 Haskellのモナドを利用してコモナドを定義する
モナドを攻略するという記事の中で、Haskellでのモナドの定義は以下のように記した。
class Applicative m => Monad m where (>>=) :: forall a b. m a -> (a -> m b) -> m b (>>) :: forall a b. m a -> m b -> m b m >> k = m >>= \_ - > k return :: a -> m a return = pure fail :: String -> m a fail s = errorWithoutStackTrace s
さらに、これらのメソッドは単位律と結合律を満足する。
上の定義で、\((>>=)\)は次のように書き換えることも可能である。2,4番目のメソッドを省いてモナドを定義すると次のようになる。
class Applicative m => Monad m where (>=>) :: forall a b c. (a -> m b) -> (b -> m c) -> (a -> m c) return :: a -> m a
これより\((>=>)\)が、関数の合成に似ていることに気がつくと思う。即ち、次のように類似している。
(.) :: (a -> b) -> (b -> c) -> (a -> c) (>=>) :: Monad m => (a -> m b) -> (b -> m c) -> (a -> m c)
一般にモナドへの射をクライスリ射と呼ぶ(上記の\(a \rightarrow m \ b, b \rightarrow m \ c\)はクライスリ射)ので、この合成は左から右へのクライスリ射の合成と呼ばれる。
さらに、恒等射についても次のように類似する。
id : a -> a return :: Monad m => a -> m a
それでは、コモナド定義してみよう。矢印の向きを変えればよいので、次のようになる。なお、モナドの場合には、\(Functor\)と\(M onad\)の間に\(Applicative\)というクラスが存在したが、コモナドの場合にはそのようなものがないので、\(Functor\)から継承することにする。
class Functor w => Comonad w where (=>=) :: forall a b c. (w a -> b) -> (w b -> c) -> (w a -> c) extract :: w a -> a
なお、これらのメソッドは単位律、結合律は満たすものとする。また\((>=>)\)の場合と同様に、\((=>=)\)を左から右へのコクライスリ射の合成という。
Haskellではインスタンスを作り出してメソッドを使えるようにすることが重要だ。そこで、データ型を用意して、メソッドを実装することを考えてみよう。コモナドはカプセルをはずして中身を取り出すようになっているので、(任意の)データ型\(a\)が環境としての(任意の)データ型\(e\)でカプセル化されており、関数\(f\)によって、(任意の)データ型\(b\)が取り出されると考えよう。即ち、Haskellで記述すると、
f :: (a,e) -> b
と考える。即ち、\(a\)と\(e\)の積と考えて、次のようなデータ型を用意しよう。
data Prod e a = Prod e a
それではデータ型\(Prod \ e \ a\)をコモナドのインスタンスとして定義しよう。これは次のようになる。
instance Functor (Prod e) where fmap f (Prod e a) = Prod e (f a) instance Comonad (Prod e) where f =>= g = \(Prod e a) -> let b = f (Prod e a) c = g (Prod e b) in c extract (Prod e a) = a
それではプログラムを使った例を示そう。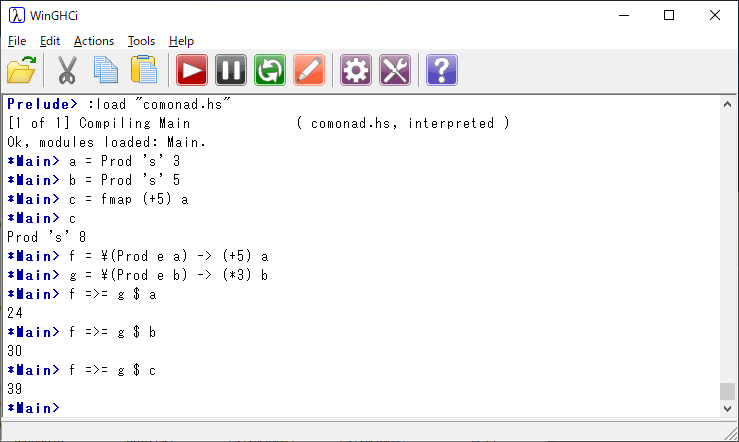
プログラムのコードは次のようになっている。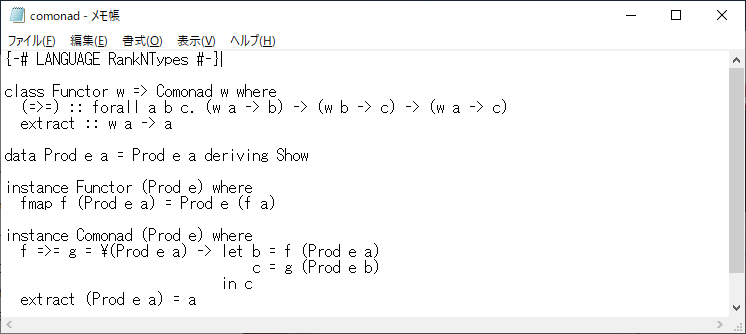
2.5 Haskellのコモナドから圏論でのコモナドへ
圏論でのコモナドは、\(extract\)と\(duplicate\)を用いて定義していた。そこで、Haskellの定義から導き出すことにしよう。
\((=>=)\)の定義の中では二つの関数を入力にしている。即ち\(f : w \ a \rightarrow b\)と\(g: w \ b \rightarrow c\)である。\(g\)は入力として\(w \ b\)を必要とするので、\(f\)を利用して\(w \ b\)を出力するような関数\(extend\)を定義しよう。これは次のようになる。
extend :: (w a -> b) -> w a -> w b
このようにすると、
(=>=) f g = g . extend f
となる。
プログラムは下記のようになる。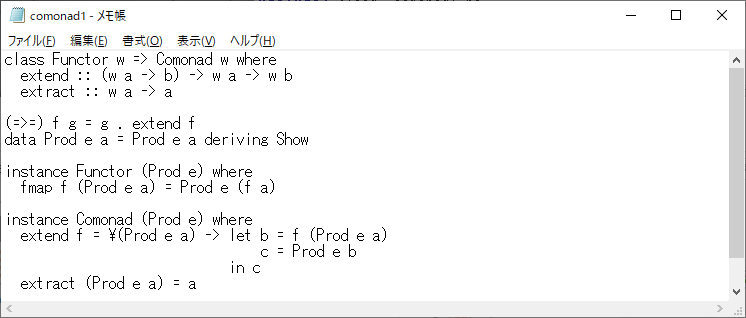
それでは\(duplicate\)から\(extend\)が得られることを示そう。そのために\(duplicate\)を次のように定義しておこう。
duplicate :: w a -> w (w a)
一方\(extend\)は
extend :: (w a -> b) -> w a -> w b
であり、射\( (w \ a \rightarrow b)\)を利用している。そこで、この射を関手\(w\)で持ち上げることを考えよう。\(fmap\)は次のように次のように定義されていた(なお、下での\(f\)は、紛らわしいのだが、関手であり、これまでの\(f\)とは別物だ)。
fmap :: (a -> b) -> f a -> f b
従って、
fmap :: (w a -> b) -> w (w a) -> w b
である。
これより、
extend f (w a) = fmap f (duplicate (w a))
となる。\( w \ a \)は任意なので、上の式は、
extend f = fmap f . duplicate
となり、さらに、
extend id = fmap id . duplicate
即ち、
extend id = duplicate
となる。
従って、コモナドは以下のように\(duplicate\)と\(extract\)を用いて表すことができる。
class Functor w => Comonad w where duplicate :: w a -> w (w a) extract :: w a -> a extend f = fmap f . duplicate (=>=) f g = g . extend f
もちろん、これらのメソッドは単位律と結合律を満足しなければならない。
2.6 信号処理をコモナドで実現する
信号処理の原理について説明したが、コモナドの概念が分かってきたところで、これを実際に使ってみよう。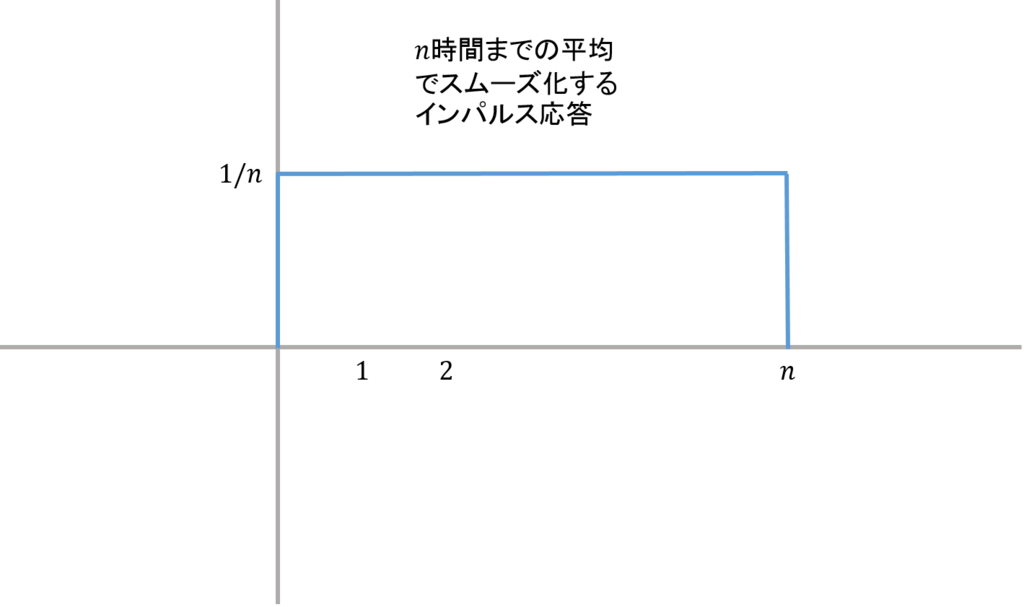
式で表すと次のようになる。
\begin{eqnarray}
g(n) =\frac{1}{n} \sum^n_{m=0}f(m)
\end{eqnarray}
極めて簡単な式だ。そこで、入力信号をストリームで表すことにし、データ型\(Stream\)を用意しよう。
data Stream a = Cons a (Stream a) | Null deriving Show
上の定義で、\(Cons \ a\)の\(a\)が現時点の入力信号だ。そして、\(Stream \ a\)はそれ以前の入力信号の列で新しいものほど左側にある。
instance Functor Stream where fmap f Null = Null fmap f (Cons a as) = Cons (f a) (fmap f as) instance Comonad Stream where extract (Cons a _) = a duplicate Null = Null duplicate (Cons a as) = (Cons (Cons a as) (duplicate as))
上の定義で、duplicateはストリームのストリームを作っている。そして、最初のストリームは、現時点までの入力信号の列である。そして、次のストリームは、一つ前の時点までに受けた入力信号の列である。
それでは、ある時点までの入力信号の列をストリームの形で受けたときの、その時点での出力信号を求めてみよう。先の式で示したように、ストリームの最初から\(n\)個までの入力信号を足し合わせ(以下のプログラムでは\(sumN\)である)、それらを\(n\)で割ればよい(以下のプログラムでは\(aveN\)である)ので、次のようになる。
sumN :: Num a => Int -> (Stream a) -> a sumN n Null = 0 sumN n (Cons a as) = if n <= 0 then 0 else a + (sumN (n-1) as) aveN :: Fractional a => Int -> Stream a -> a aveN n Null = 0 aveN n stm = (sumN n stm) / (fromIntegral n)
これを、現時点までの入力信号の列、一つ前までの入力信号の列、二つ前までの入力信号の列、…からそれぞれ出力信号を得れば、現時点までの出力信号の列を得ることができる。従って、
outN :: Fractional a => Int -> (Stream a) -> (Stream a) outN n Null = Null outN n stm = fmap (aveN n) (duplicate stm)
となる。
この式は以下のようにしてもよい。
outN :: Fractional a => Int -> (Stream a) -> (Stream a) outN n Null = Null outN n stm = extend (aveN n) stm
少し簡単すぎたので、もう少し一般的な信号処理を扱ってみよう。
インパルス応答は、現在の時間での応答、次の時間が来たときの応答、その次の時間が来たときの応答というように、入力信号列と同様に、ストリームで表すことができる。そこで、ある時点までの入力信号の列が与えられているときに、そのときの出力は次のように表すことができる。
以下のプログラムで、\(zipstream\)はある時点での出力信号を求めるためのものである。これはストリームになっていて、この時点に入ってきた入力信号に対するこの時点の出力信号、その一つ前の時点で入ってきた入力信号に対するこの時点の出力信号、さらに一つ前の入力信号に対するこの時点の出力信号となっている。即ち、この時点までに入ってきた入力信号からの子の時点での出力信号の列である。\(zipstream\)は三つの入力を受ける。それらは \( f \ inp \ stm\)で、\(inp\)はインパルス応答、\(stm\)は入力信号である。なお、\(f\)はインパルス応答と入力信号のそれぞれに対する演算で、この場合は常に乗算である。
また、\(conv\)はある時点での出力信号の総和をとる。
zipstream :: Num a => (a -> a -> a) -> (Stream a) -> (Stream a) -> (Stream a) zipstream f Null _ = Null zipstream f _ Null = Null zipstream f (Cons a as) (Cons b bs) = Cons (f a b) (zipstream f as bs) conv :: Num a => (Stream a) -> a conv Null = 0 conv (Cons a as) = a + (conv as)
\(out\)は現時点までの出力信号の列である。
outC :: Num a => (Stream a) -> (Stream a) -> (Stream a) outC inp stm = fmap conv (extend (zipstream (*) inp) stm) --outC inp stm = fmap conv (fmap (zipstream (*) inp) (duplicate stm))
それでは利用してみよう。例として用いるのは信号処理の原理を説明したときの例だ。もう一度図を表示しよう。
stm = Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons 0 (Cons (-2.5) (Cons 0.8 (Cons 2.8 (Cons 1.4 (Cons 1 Null)))))))))))))))
インパルス応答の図は、左側に行くほどより以前に来た入力に応答するようになっているので、左側がストリームの先頭になるようにする。従って次のようになる。
inp = Cons 0 (Cons 0.53 (Cons 0.42 (Cons 0.13 (Cons (-0.05) (Cons (-0.09) (Cons (-0.05) (Cons (-0.01) (Cons 0.01 (Cons 0.01 (Cons 0.01 (Cons 0 Null)))))))))))
全体のプログラムを示しておこう。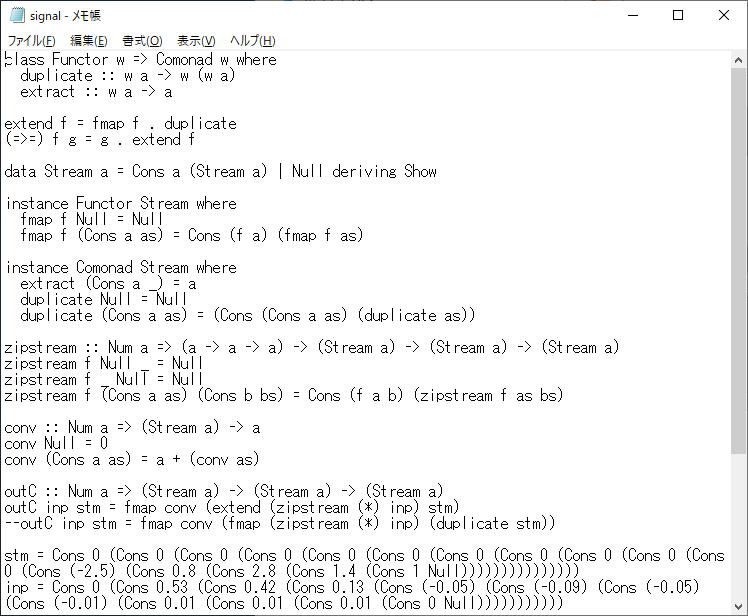
これを実行してみよう。結果は次のようになる。ストリームの左側の方が新しい出力である。プログラムの実行結果を見ると、図の値と同じであることが分かり、プログラムが適切に機能していることが分かる。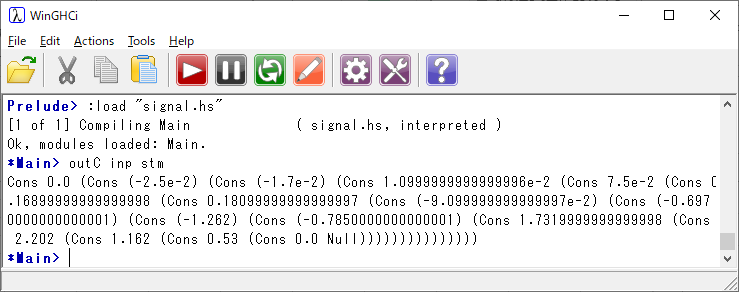
信号処理での畳み込みのプログラムが、このようにすっきりと短いコードで書き表せるのはHaskellの特徴だ。C言語で書いていた時のわずらわしさは、ここにはない。
2.7 圏論でのコモナド
それではHaskellから圏論へと場面を変えることにしよう。Haskellで用いた関数\(duplicate,extract\)は、圏論では自然変換と考えるのがよい。このようにすると、
extract:: w a -> a
は下図のように考えることができる。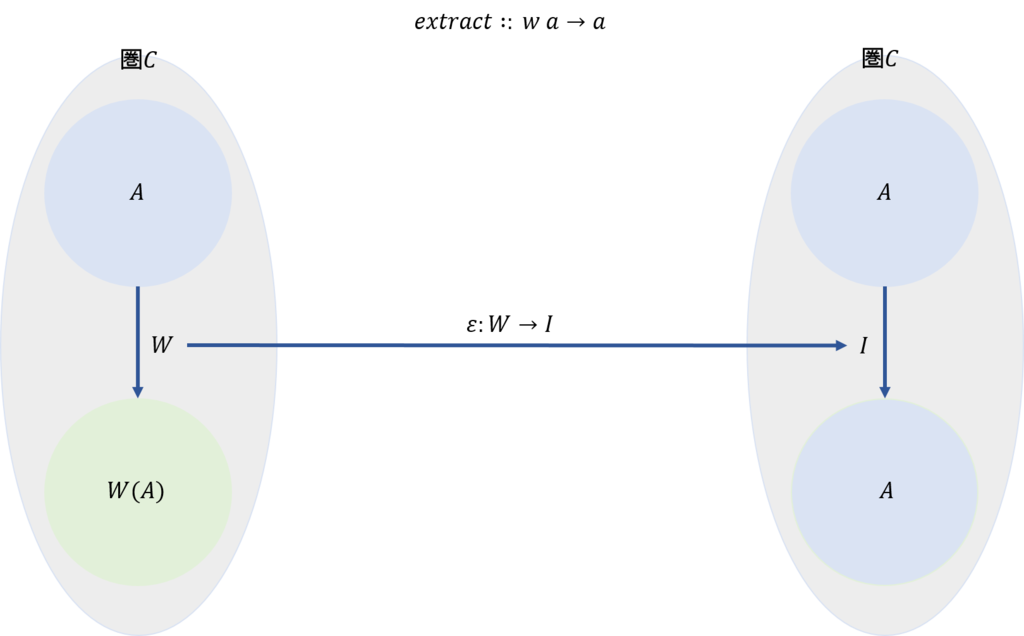
すなわち\(w \ a\)は関手\(W:A \rightarrow W(A)\)と見なすことができ、\(a\)は関手\(I:A \rightarrow A\)と見なすことが可能である。この結果、\(extract\)は自然変換\(ε:W \rightarrow I \)とすることができる。
同様に、\(duplicate\)は下図に示すように\(δ:W \rightarrow W \circ W\)とすることができる。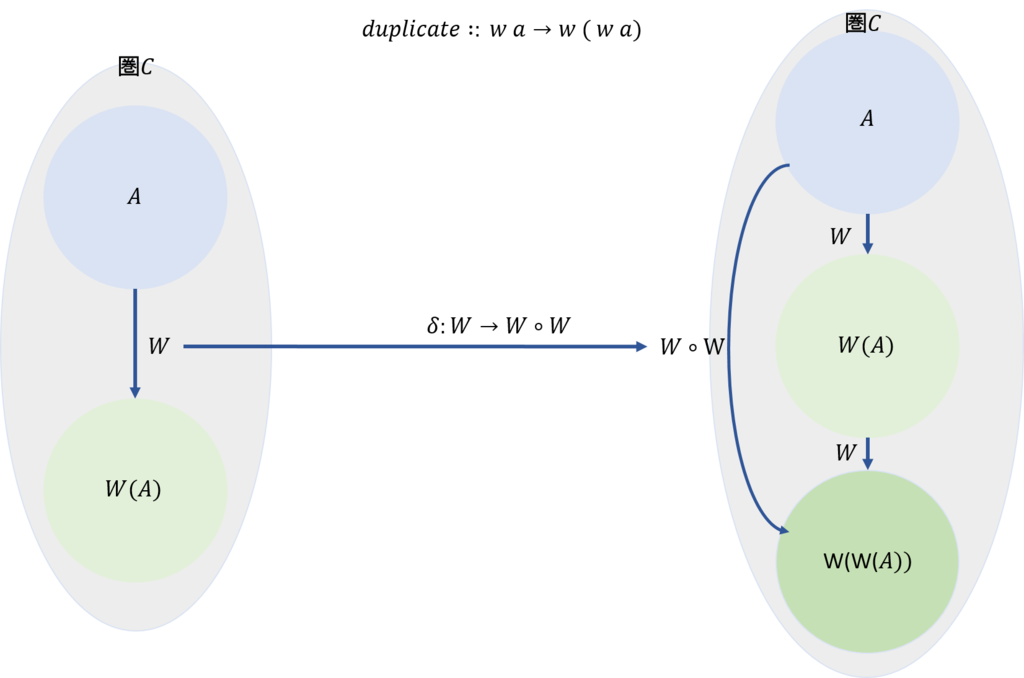
また、単位律、結合律が守られることから、これを可換図式で表すと下図が得られる。右側の二つの図は、コモナドの三角恒等式と呼ばれるものだ。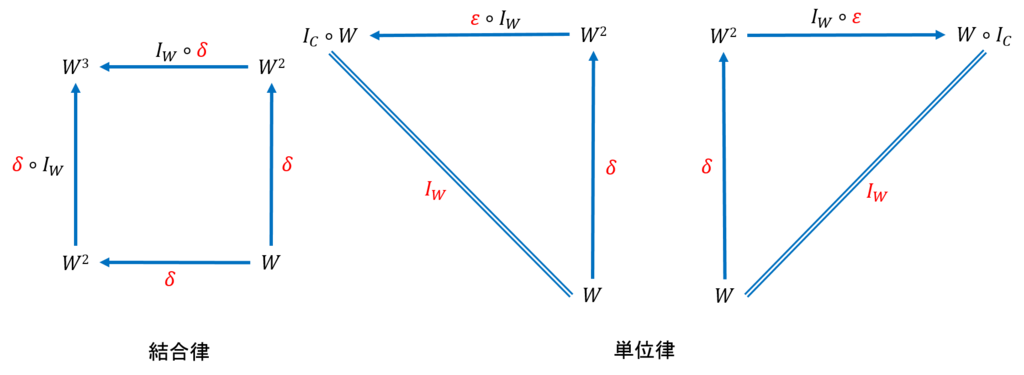
それでは、コモナドの圏を定義しておこう。
コモナドの圏の構成
対象:\(I_C,W,W \circ W, W \circ W circ W,…\)
射:\(ε:I_C \rightarrow W, δ:W \rightarrow W \circ W\)
恒等射:\(I_W\)
合成:\( \circ \)
結合律:\( δ \circ (I_W \circ δ) = δ \circ (δ \circ W) \)
単位律:\(( ε \circ I_W) \circ δ = I_W = (I_W \circ ε) \circ δ \)
図で表すと以下のようになる。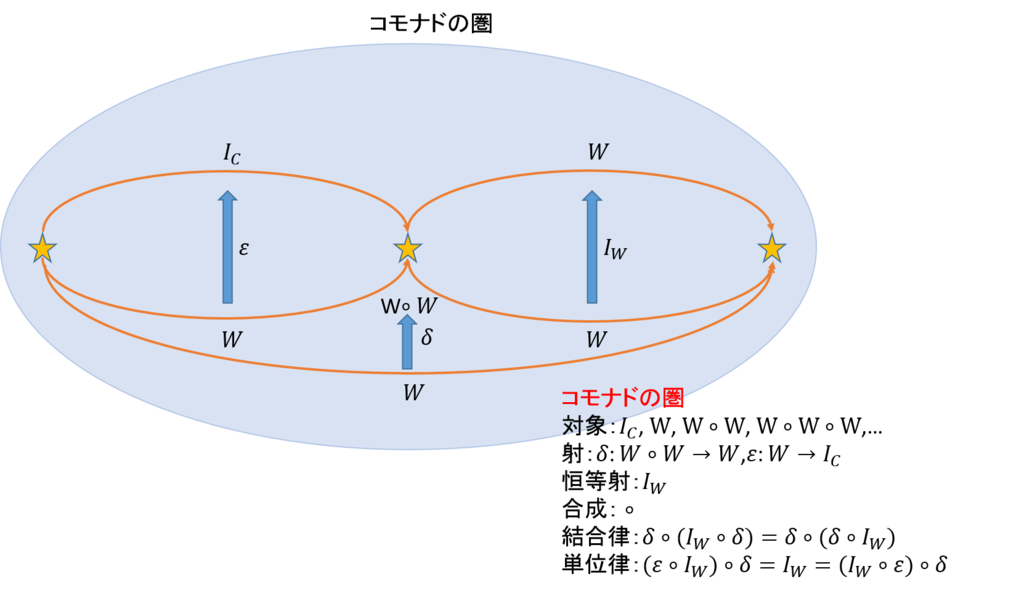
2.8 コモナドと随伴との関係
それではコモナドと随伴との関係を見てみよう。随伴には、内容は同じだが複数の定義がある。余単位(counit)・単位(unit)随伴はその中の一つで、それは次のようになっている。
圏\(\mathcal{C}\)と\(\mathcal{D}\)の余単位・単位随伴は二つの関手
\begin{eqnarray}
L: \mathcal{D} \rightarrow \mathcal{C} \\
R: \mathcal{C} \rightarrow \mathcal{D}
\end{eqnarray}
および二つの自然変換
\begin{eqnarray}
η: I_\mathcal{D} \rightarrow R \circ L \\
ε: L \circ R \rightarrow I_\mathcal{C}
\end{eqnarray}
であって(ηは単位、εは余単位と呼ばれる)、これらの合成
\begin{eqnarray}
L =L \circ I_\mathcal{D} \xrightarrow{L \circ η} L \circ R \circ L \xrightarrow{ε\circ L} L \\
R = I_\mathcal{D} \circ R \xrightarrow{η\circ R} R \circ L \circ R \xrightarrow{R \circ ε} R
\end{eqnarray}
がそれぞれ\(L\)と\(R\)上の恒等変換\(I_L,I_R\)となることである。これは三角恒等式(triangle identities)と呼ばれる。
図で表してみよう。随伴の定義に関する図は次のようになっている。
また、三角恒等式を関図式で表すと次の通りだ。
\begin{eqnarray}
W=L \circ R
\end{eqnarray}
としてみよう。コモナド側の\(ε\)を得ることは簡単だ。
\begin{eqnarray}
ε : I_\mathcal{D} \xrightarrow{ε} L \circ R = W
\end{eqnarray}
それでは\(δ\)について考えよう。次のようにすればよい。
\begin{eqnarray}
δ : W = L \circ R = L \circ I_D \circ R \xrightarrow{L \circ η \circ R} L \circ R \circ L \circ R = W \circ W
\end{eqnarray}
コモナドの圏での単位律、結合律も同じように得られるので試みて欲しい。