6.3 随伴
随伴は、圏論を代表する概念である。これは、「二つの圏が全く同じとは言わないまでもとても似ている」という考え方を与える。二つの圏\( \mathcal{C,D} \)が与えられた時に、\(LR=I_\mathcal{C}\)と\(RL=I_\mathcal{D}\)を満たすような関手\(L: \mathcal{D} \rightarrow \mathcal{C} \)と関手\(R: \mathcal{C} \rightarrow \mathcal{D} \)が存在するならば、二つの圏は同値、すなわち全く同じである。しかし、二つの圏が同値という考え方は、膠着しすぎていて、あまり面白くない。そこで、少し緩めて、図10に示すように、自然変換
\begin{eqnarray}
ε: LR \rightarrow I_\mathcal{C} \\
η: I_\mathcal{D} \rightarrow RL
\end{eqnarray}
が成り立つならば、同じと考えようというのが随伴である(一般には\(L,R\)は\(F,G\)を用いて記述されるが、どちらを向いている関手であったかが分かりにくくなるので、ここでは矢印の向きを明示してくれる\(L,R\)を用いる)。また随伴は図10の下半分に示してあるcounit-unit恒等式を満たさなければならない。 図10:随伴の定義最初の\(ε\)はcounitと呼ばれる自然変換である。これは図11に示すように、\( \mathcal{C} \)の任意の対象\(A\)を、\(R\)で\( \mathcal{D} \)に移し、さらにそれを\(L\)で\( \mathcal{C} \)に移す。少し飛躍的な表現で説明するならば、\(\forall A \)に対して\( ε_A: LR(A) \rightarrow I_\mathcal{C}(A) \)によって、「本当の自分に戻れる」ということを表している。
図10:随伴の定義最初の\(ε\)はcounitと呼ばれる自然変換である。これは図11に示すように、\( \mathcal{C} \)の任意の対象\(A\)を、\(R\)で\( \mathcal{D} \)に移し、さらにそれを\(L\)で\( \mathcal{C} \)に移す。少し飛躍的な表現で説明するならば、\(\forall A \)に対して\( ε_A: LR(A) \rightarrow I_\mathcal{C}(A) \)によって、「本当の自分に戻れる」ということを表している。 図11:随伴を構成する自然変換counit二番目の自然変換\(η\)はunitと呼ばれる自然変換である。これは図12に示すように、\( \mathcal{D} \)の任意の対象\(B\)を、\(L\)で\( \mathcal{C} \)に移し、さらにそれを\(R\)で\( \mathcal{D} \)に移す。同じように飛躍的な表現を用いれば、\(\forall A \)に対して\( η_A: I_\mathcal{D} (A) \rightarrow RL (A)\)によって、「自分を別のかたちで表現できる」ということを表している。
図11:随伴を構成する自然変換counit二番目の自然変換\(η\)はunitと呼ばれる自然変換である。これは図12に示すように、\( \mathcal{D} \)の任意の対象\(B\)を、\(L\)で\( \mathcal{C} \)に移し、さらにそれを\(R\)で\( \mathcal{D} \)に移す。同じように飛躍的な表現を用いれば、\(\forall A \)に対して\( η_A: I_\mathcal{D} (A) \rightarrow RL (A)\)によって、「自分を別のかたちで表現できる」ということを表している。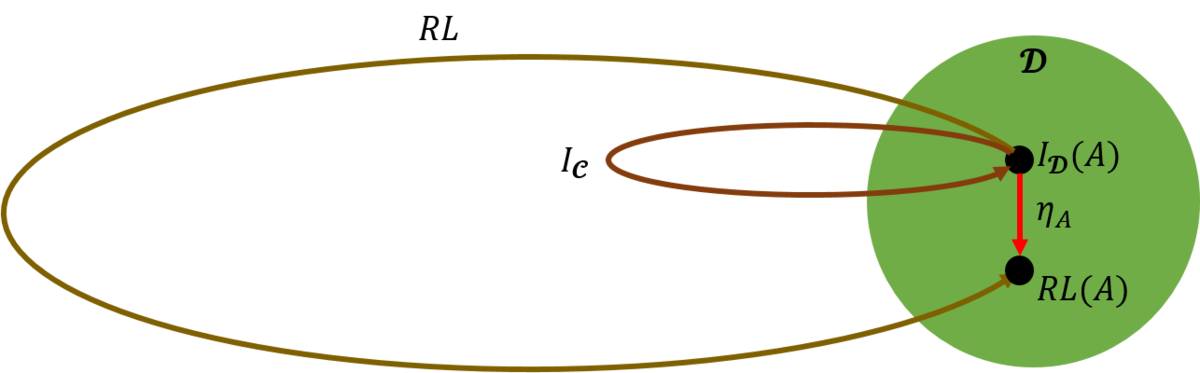 図12:随伴を構成する自然変換unit世の中には「別のかたちで表現するもの」は沢山ある。戦国時代の「かぶく」というのもその一つの例だろうが、身近なところでは、感情と表情の関係だ。人間には、嬉しいとか悲しいとか怒っているとかいう感情があるが、そのときどきに抱いている感情は、表情として顔に現れる。このため、顔に現れる表情は、内面にある感情を「別のかたちで表現している」と見なすことができ、自然変換のunitと考えていいだろう。逆に、顔の表情から内面の感情を知ろうとするのが、「本当の自分に戻る」ということになる。これはcounitである。圏論を定義する自然変換は、このように重要な概念を与えてくれるので、自然科学だけではなく、人文科学や社会科学にも、その応用分野を広げてくれ、とても有用である。
図12:随伴を構成する自然変換unit世の中には「別のかたちで表現するもの」は沢山ある。戦国時代の「かぶく」というのもその一つの例だろうが、身近なところでは、感情と表情の関係だ。人間には、嬉しいとか悲しいとか怒っているとかいう感情があるが、そのときどきに抱いている感情は、表情として顔に現れる。このため、顔に現れる表情は、内面にある感情を「別のかたちで表現している」と見なすことができ、自然変換のunitと考えていいだろう。逆に、顔の表情から内面の感情を知ろうとするのが、「本当の自分に戻る」ということになる。これはcounitである。圏論を定義する自然変換は、このように重要な概念を与えてくれるので、自然科学だけではなく、人文科学や社会科学にも、その応用分野を広げてくれ、とても有用である。
\(ε,η\)をpasting diagramで示すと図13になる。 図13:自然変換\(ε,η\)をpasting diagramで表す
図13:自然変換\(ε,η\)をpasting diagramで表す
それでは随伴をストリング・ダイアグラムで表すことにしよう。
自然変換\(ε,η\)は、pasting diagramをストリング・ダイアグラムに変換する方法を用いれば簡単に求めることができ、図14のようになる。 図14:随伴を定義する自然変換をPsting diagramで表現する
図14:随伴を定義する自然変換をPsting diagramで表現する
それでは、counit-unit恒等式について考えよう。これをpasting diagramで表すと図15のようになる。  図15:counit-utit恒等式をpasting diagramで表すそれでは、図15の右上のpasting diagramをストリング・ダイアグラムに変換すると図16のようになる。
図15:counit-utit恒等式をpasting diagramで表すそれでは、図15の右上のpasting diagramをストリング・ダイアグラムに変換すると図16のようになる。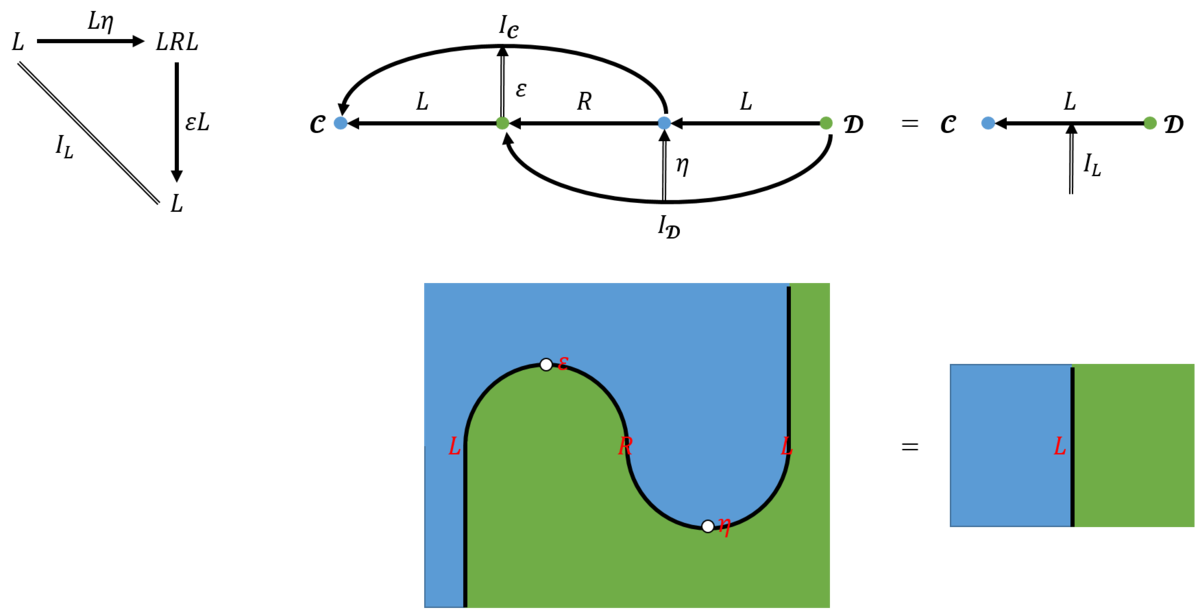 図16:counit-utit恒等式をストリング・ダイアグラムで表す―その1そして、図15の右下のpasting diagramをストリング・ダイアグラムに変換すると図17のようになる。
図16:counit-utit恒等式をストリング・ダイアグラムで表す―その1そして、図15の右下のpasting diagramをストリング・ダイアグラムに変換すると図17のようになる。 図17:counit-utit恒等式をストリング・ダイアグラムで表す―その2Counit-unit恒等式は、ストリング・ダイアグラムで表すとジグザクな線になるので、ジグザグ恒等式(zig-zag equations)と呼ばれる。
図17:counit-utit恒等式をストリング・ダイアグラムで表す―その2Counit-unit恒等式は、ストリング・ダイアグラムで表すとジグザクな線になるので、ジグザグ恒等式(zig-zag equations)と呼ばれる。
随伴をストリング・ダイアグラムで表すことができたので、つぎはモナドに挑戦しよう。







