6.1 圏の圏
中学に入学すると、算数に代わって数学という教科が登場する。計算問題が嫌いだった私は、嫌なことから解放してくれるような、楽しいパラダイムがきっと待ち受けているのだろうと、過剰に期待した。しかし、真っ先に学んだのは、三角形の合同や相似だった。中間試験や期末試験では、図形内の二つの三角形が合同であることを証明しなさいというような問題が出題された。なんと嫌なことに補助線を見つけられるかどうかが勝敗を分けた。博打的な要素があり、あまり好きになれず、期待は裏切られた。
今回の記事は、その幾何学を用いて、圏を表してみようという話である。圏論は、「数学の数学」と言われるほどに抽象的な概念で説明しにくいのだが、それが目に見えるような形で表わせれば、とても理解しやすいものになるだろうし、面白いことにもなりそうだ。そして中学生の時に味わった憂鬱な気分を払拭してくれるかもしれない。それにもましたこのビジュアルな表現を用いて、定理の証明がいとも簡単に行えることが示せれば、感動さえ覚えそうに思える。このような期待を込めて、ビジュアルな表現を紹介しよう。
ここでは、1) (小さな)圏を対象とし、2) 関手を射とし、3) 関手間の射を自然変換とした、圏\(\rm{Cat}\)(圏の圏と呼ばれる)を考えることにしよう(このようにすると、自然変換の立ち位置が何とも定まりが悪いので、関手を対象とし、自然変換を射とした圏を考える方が本当は自然である。実際、このように定義したものをStrict 2-categoryと呼ばれる。ここでは前からのつながりもあるので、\(\rm{Cat}\)を用いて説明する)。
圏に関する用語と例
簡単に圏論の中で使われる用語を説明しておこう。
1)圏は、どのように計算したらよいかを示してくれる構造である。
2)関手は、ある圏の計算の構造を、他の圏に移すものだ(他の圏は元のある圏であっても構わない。このときは、自身に計算の構造をもちこむこととなる)。
3)自然変換は、ある圏から他の圏への二つの関手の間での関係を示すものだ。
具体的なイメージがつかめるように、それぞれの用語な例を挙げておこう。
1)圏の例:圏は対象、射、ドメインとコドメイン、恒等射、合成で構成され、単位律、結合律を満たす。
例1:加算を有する正数(0以上の整数):これを圏\(\mathcal{C}\)とする。\(\mathcal{C}\)は次のように構成される。射は整数の一つ一つ、即ち、0,1,2,...である。恒等射は0。合成は加算\(+\)。射は写像と考えてよいので、入力(これはドメインと呼ばれる)と出力(これはコドメインと呼ばれる)を有する。ドメインやコドメインになるものが対象である。この場合、射は整数なので、ドメインとコドメインを考えにくいが、定義上必要とするので、通常は一要素を対象とし、★で表わす。
例2:正数が並んだリスト(例えば\([2,4,5]\) ):これを圏\(\mathcal{D}\)とする。\(\mathcal{D}\)は次のように構成される。射はそれぞれのリスト。恒等射は空のリスト[ ]。合成はリストの接続\(++\)。対象、ドメイン、コドメインは★。
2) 関手の例:
例1:リストに加法をもちこむ:任意のリストを\([b_0,b_1,b_2,....]\)としたとき、これに任意の正数\(a\)を加えるという関手\(F\)は、\([b_0+a,b_1+a,b_2+a,....]\)の計算をすることである。
例2:リストに剰余類による加算をもちこむ:同じように任意のリストを\([b_0,b_1,b_2,....]\)としたとき、これに任意の正数\(a\)を加えてその剰余\(m\)を求めるという関手\(G\)は、\([Mod_m(b_0+a),Mod_m(b_1+a),Mod_m(b_2+a,....])\)の計算をすることである。
3)自然変換の例
例1:\(F\)から\(G\)への自然変換\(α\)は、\([b_0+a,b_1+a,b_2+a,....]\)から\([Mod_m(b_0+a),Mod_m(b_1+a),Mod_m(b_2+a,....])\)への変換をすることである。即ち、リストの要素ごとに剰余を求める計算を行うことになる。
自然変換の合成
それでは自然変換の合成について若干説明しておこう。これには、水平方向への合成と垂直方向の合成がある。
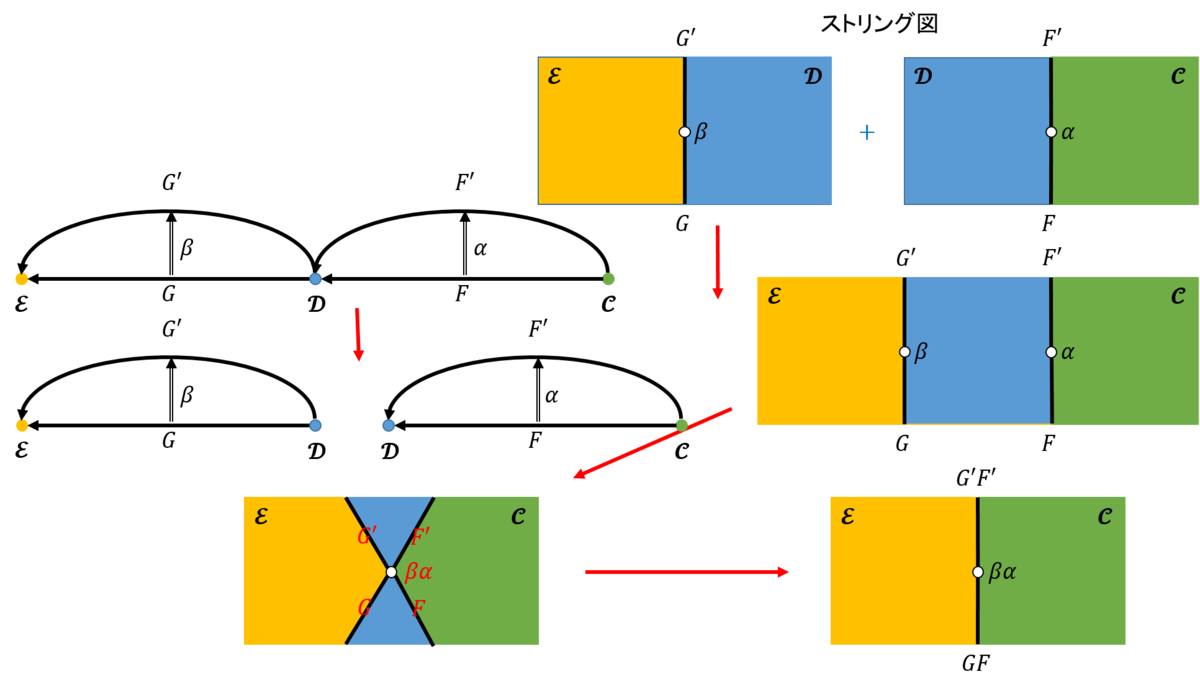
水平方向の合成は次のようになる(図1参照)。水平に配置された圏を\(\mathcal{C,D,E}\)としよう。\(\mathcal{C,D}\)の間では関手\(F,G : \mathcal{C} \rightarrow \mathcal{D} \)が、\(\mathcal{D,E,}\)の間では関手\(F’,G’ : \mathcal{D} \rightarrow \mathcal{E} \)が、二つの関手間にはそれぞれ自然変換\(α:F \Rightarrow G,\)と\(β:F’ \Rightarrow G’ \)が定義されているとしよう。このとき、この自然変換の合成は\(βα:F’ F \Rightarrow G’ G : \mathcal{C} \rightarrow \mathcal{E}\)となる。
垂直方向の合成は次のようになる(同じく図1参照)。圏を二つ用意して\(\mathcal{C,D}\)としよう。\(\mathcal{C,D,}\)の間では関手\(F,G,H : \mathcal{C} \rightarrow \mathcal{D} \)が、二つの関手間にはそれぞれ自然変換\(α:F \Rightarrow G, γ:G \Rightarrow H \)が定義されているとしよう。このとき、この自然変換の合成は\( γ α : F \Rightarrow H : \mathcal{C} \rightarrow \mathcal{D} \)となる。
次に、水平方向と垂直方向の両方の合成が可能である場合を考えることにしよう。図1のように、圏\(\mathcal{C,D,E}\)が、関手\(F,G,H : \mathcal{C} \rightarrow \mathcal{D}\),\(F’,G’,H’ : \mathcal{D} \rightarrow \mathcal{E}\)が、自然変換\(α:F \Rightarrow G, β:F' \rightarrow G',γ: G \Rightarrow H, δ: G’ \Rightarrow H’ \)が定義されているとしよう。このとき、垂直方向に合成したあと水平方向に合成することも可能であるし、水平方向に合成したあと垂直方向に合成することも可能である。前者の場合には\((δβ)(γα)\)、後者の場合には\((δγ)( βα)\)となる。このとき、\(\rm{Cat}\)では交換律(interchange law:合成の順序に依らない)が成り立つ。すなわち\(δβγα=δγβα\)である。
6.2 ストリング・ダイアグラム
これから説明する圏の図的表現は、ストリング・ダイアグラム(String Diagram)と呼べれる。まず簡単な例から見ていこう。
圏\(\mathcal{C,D}\)とその間の関手\(F:\mathcal{C} \rightarrow \mathcal{D}\)で構成される圏の圏\(\rm{Cat}\)をpasting diagramで表したのが図2左である。この図で0-セルは0次元で、1-セルは1次元で表されている。それでは、この関係を反転させて、0-セルは1次元で、1-セルは0次元で表すと図2右となる。これがストリング・ダイアグラムの基本的な考え方である。このとき、右側の圏がドメインで、左側の圏がコドメイン、即ち、関手は右から左に向いていることに注意して欲しい。反対向きに定義している場合もあるが、こちらの方が、関手を合成したとき、並びが同じになり、分かりやすい。
それではもう少し進んで、圏\(\mathcal{C,D}\)とその間の関手\(F,G:\mathcal{C} \rightarrow \mathcal{D}\)、さらに関手の間の自然変換\(α:F \rightarrow G\)について考えよう。pasting diagramは図3左上のようになる。ストリング・ダイアグラムは次元を反転させればよいので、0-セルは2次元で、1-セルは1次元で、2-セルは0次元にする。求め方は意外と簡単で、図3左下に示すように、自然変換を表している真ん中から、それを囲んでいる関手の線分の真ん中をめがけて線を引く。これらの線が関手を表し、それぞれの線に沿った面が圏となる。分かりやすくしたのが、図3右上である。なお、この図の下の部分を表すと、図3右下となる。これはストリング・ダイアグラムの基本的な考え方を示す時に用いたときのものと同一である。なお。自然変換は、下から上に向かっていることに注意して欲しい。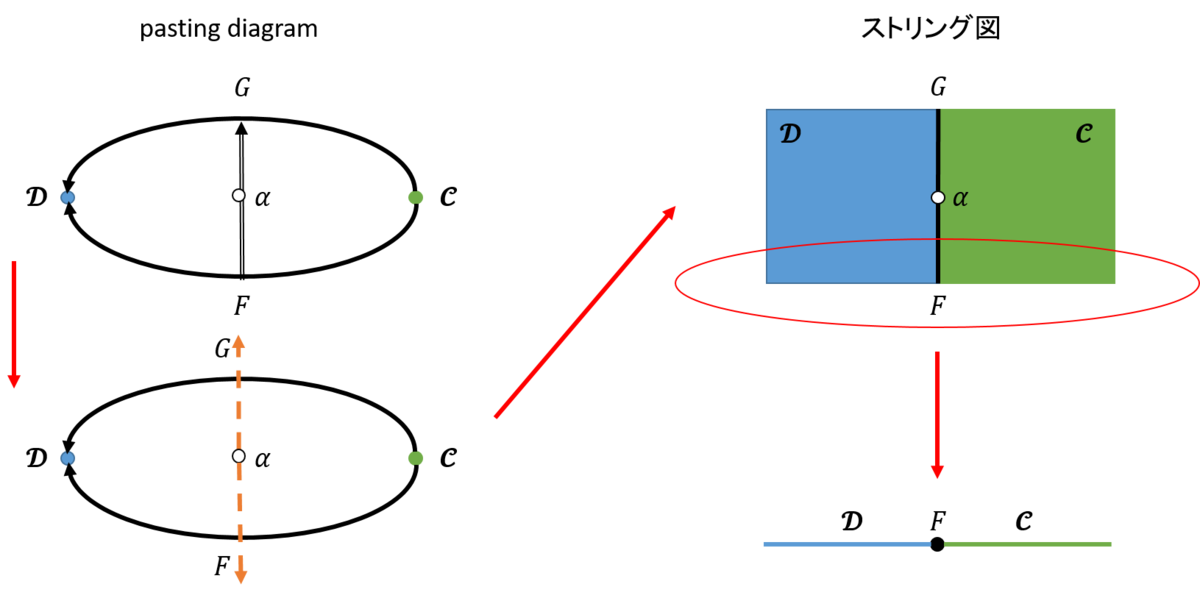
次に自然変換が恒等射になっている場合を考えてみよう。圏\(\mathcal{C,D}\)とその間の関手\(F:\mathcal{C} \rightarrow \mathcal{D}\)、さらに関手の間の自然変換\(I_F:F \rightarrow F\)について考えよう。pasting diagramにもいくつかの表し方があり、図4左のようになる。これらに対するストリング・ダイアグラムは図4右のようになる。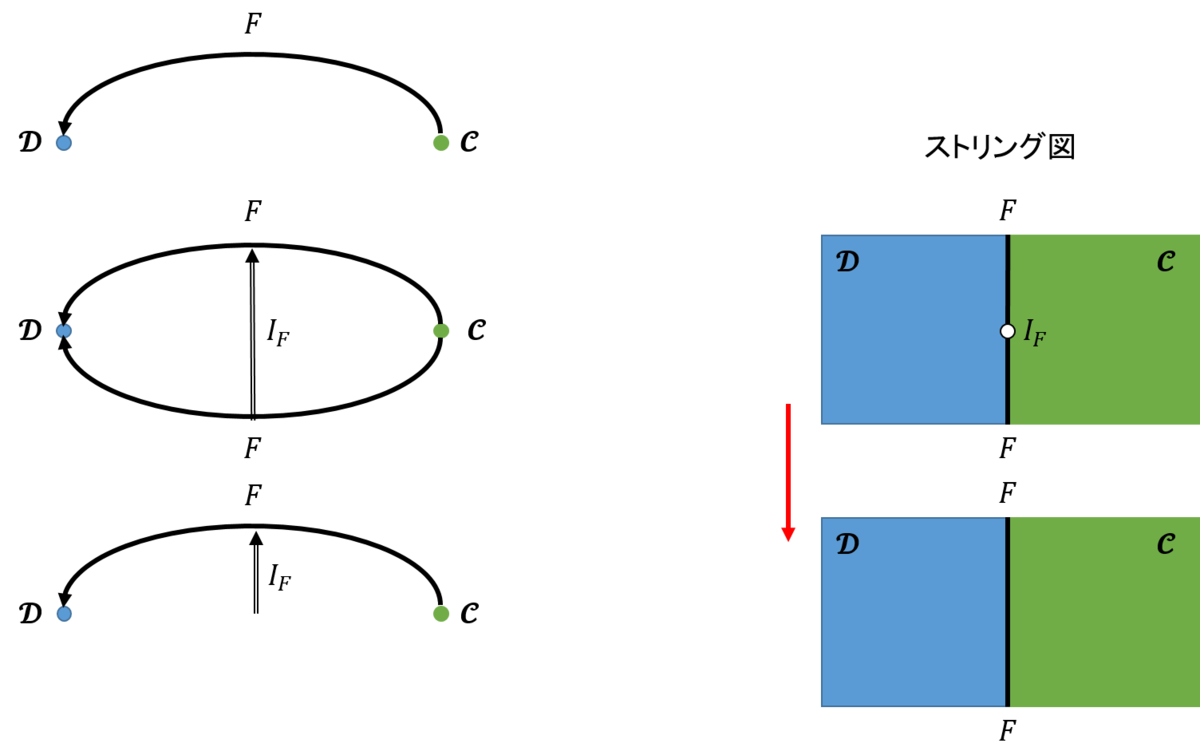
それでは、図5左のように関手の一つが恒等射の場合について考えてみよう。このときのストリング・ダイアグラムの表し方は特殊で、恒等射の関手は点線で表すか、またはそれは描かなくてもよいとする。すなわち図5右のようになる。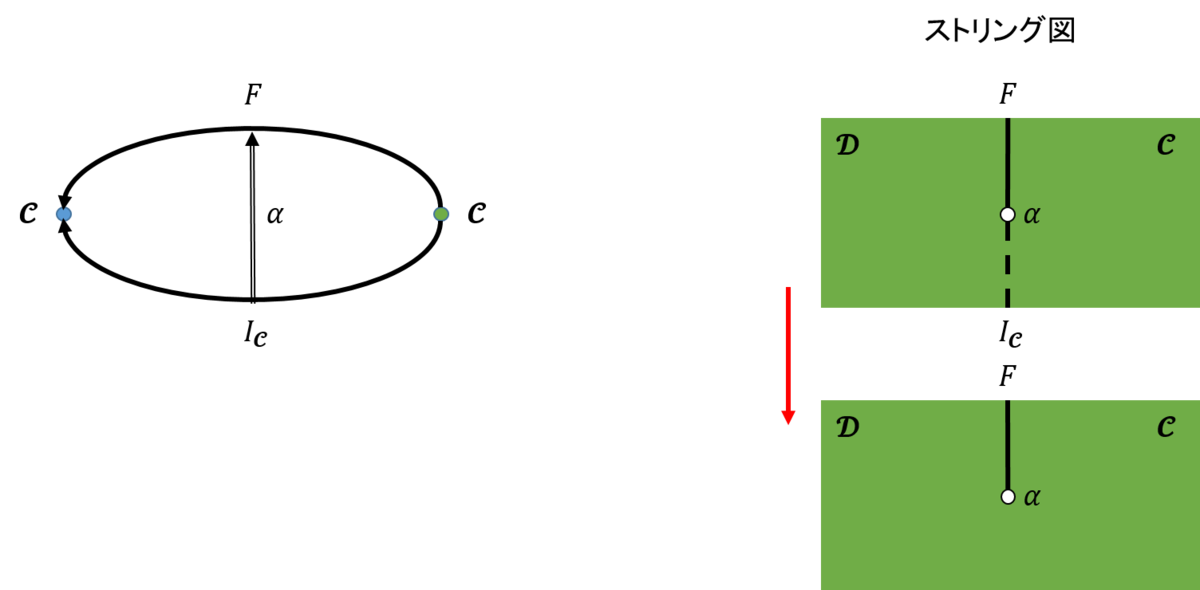
自然変換の合成を表してみよう。まず垂直方向に合成す場合を考えてみよう。図6のようになる。なお、自然変換\(α\)と\(β\)の合成\(\circ\)は、一般的には\(β \circ α\)と書かれるが、ここでは合成の記号を省いて\(βα\)とあらわすことにする。関手に対しても同じように記述する。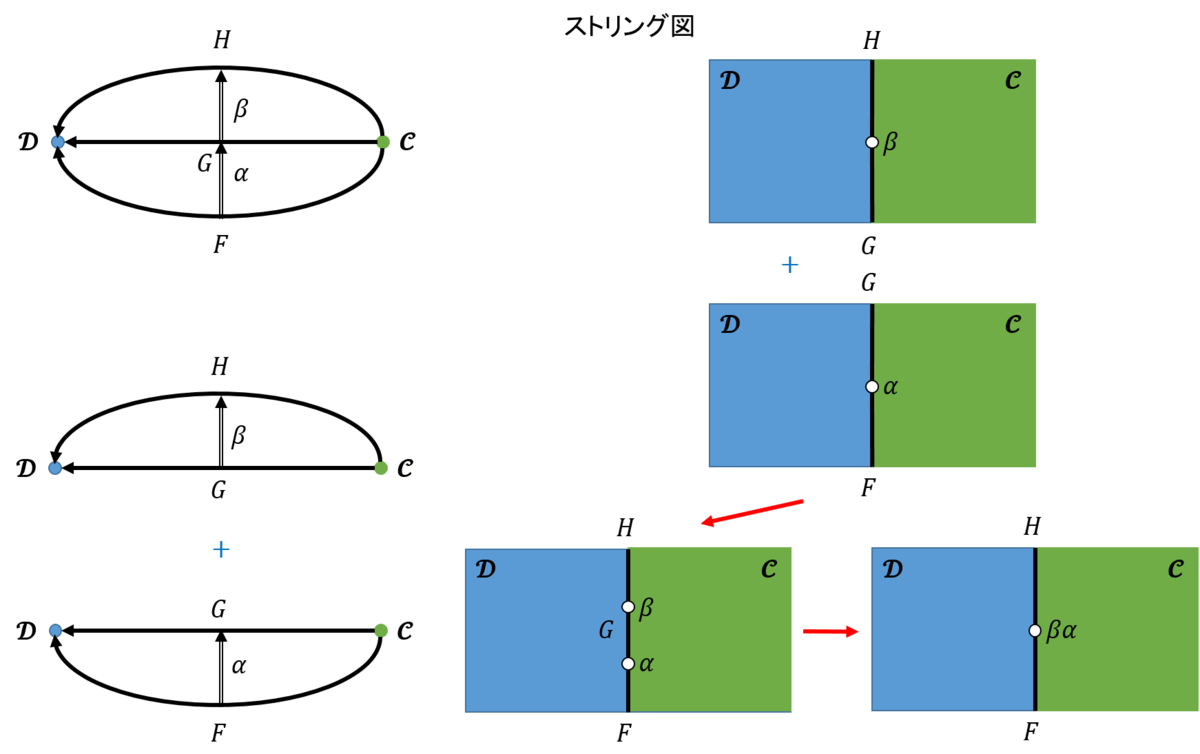


次は具体的な例として随伴を表すことにしよう。