4.米田の補題
いよいよ米田の補題の証明である。これは次のようになっている。
局所的に小さい圏\(\mathcal{C}\)(任意の2対象\(A,B\)に対して\({\rm Hom(A,B)}\)の類が集合となっているような圏)について、共変\({\rm Hom}\)関手\(h^A:\mathcal{C} \rightarrow \mathbf{Set}\)から集合値関手\(F:\mathcal{C} \rightarrow \mathbf{Set}\)への自然変換と、集合である対象\(F(A)\)の要素との間には一対一の対応が存在する。即ち、
\begin{eqnarray}
Nat (h^A,F) \cong F(A)
\end{eqnarray}
である。
あるいは、圏\(\mathcal{C}\)と圏\(\mathbf{Set}\)により作られる関手圏を\([\mathcal{C} , \mathbf{Set}]\)で表し、
\begin{eqnarray}
[\mathcal{C} , \mathbf{Set}] (h^A,F) \cong F(A)
\end{eqnarray}
が成り立つというのが米田の補題である。
4.1 証明の準備
それでは証明のための準備をしよう。米田の補題を証明するために図1を用いる。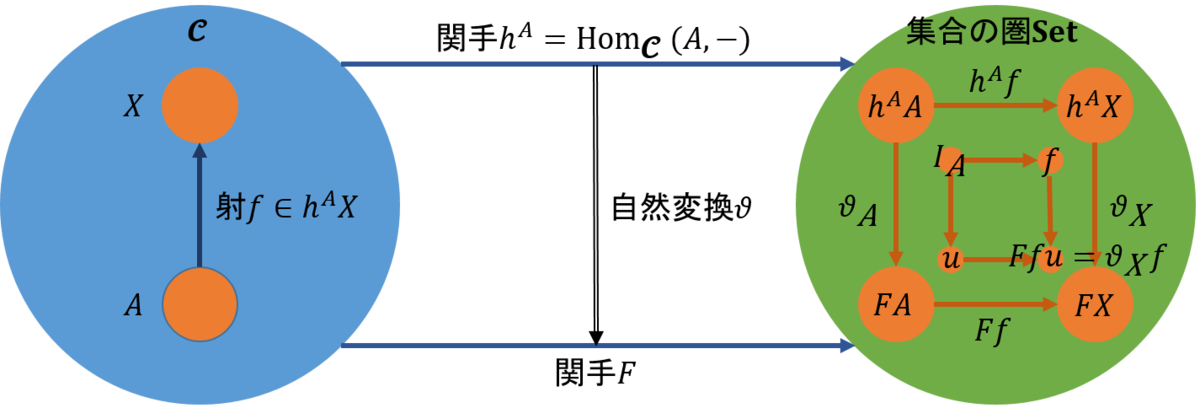
\begin{eqnarray}
φ_{F,A}:Nat (h^A,F) \cong F(A)
\end{eqnarray}
射\(φ_{FA}\)を自然変換\(\partial \in Nat(h^A,F) \)に対して、
\begin{eqnarray}
φ_{F,A}\partial=\partial_A I_A
\end{eqnarray}
と定める。
さらに、\(F(A)\)から出発して\(F(X)\)に至る経路は\(h^A(A)\)から\(h^A(X)\)を経由する場合と、直接至る場合とがあり、これらが可換である。そこで、
\begin{eqnarray}
ψ: F(A) \rightarrow Nat (h^A,F)
\end{eqnarray}
を任意の\(u \in F(A) \)に対して、
\begin{eqnarray}
ψ(u)_X (f) &=& F(f)(u) \\
f & : & A \rightarrow X
\end{eqnarray}
と定める。このとき、\(ψ(u)_X= \partial_X \)である。
米田の補題を証明するためには、次の3項目を証明すればよい。
1)\(ψ(u)\)が自然変換である。
2)\(ψ=φ_{F,A}^{-1}\)である。
3)\(F,A\)に対して自然である。
4.2 米田の補題をストリング・ダイアグラムに
米田の補題をストリング・ダイアグラムで表すことにしよう。図2に示すように、例によって圏\(1\)を設け、圏\(\mathcal{C}\)の対象\(A,X\)を、圏\(1\)から\(\mathcal{C}\)への関手として表すことにする。なお図2下はpasting diagramである。
準備のところで得た二つの式は図3のストリング・ダイアグラムになる。
4.3 米田の補題の証明
それでは順を追って証明していこう。最初の項目から始めよう。
1)\(ψ(u)\)が自然変換である。
\(ψ(u)_X=\partial_X\)であることから、\(\partial: h^A \rightarrow F\)が自然変換であることを言えばよい。即ち、任意の\(X,Y\)に対して、図4が可換になることを示せばよいので、\(h^A(X)\)から出発して\(F(Y)\)に到達する経路において、\(F(X)\)を経由する場合と\(h^A(Y)\)を経由する場合は同値であることを示せばよい。
すなわち、
\begin{eqnarray}
\partial_X & : & h^A (X) \rightarrow F(X) \\
F (g) \partial_X &=& \partial_Y h^A (g)
\end{eqnarray}
が成り立つことを示せばよい。
それではストリング・ダイアグラムを用いて証明してみよう。図5のようになる。これは、\(f:A \rightarrow g\)を利用して、\( F (g) \partial_X f = \partial_Y h^A (g (f ))
\)となることを示している。
細部を確認してみよう。図で(1)から(2)は、\(\partial_X\)を\( ψ(u)_X \)で置き換え、さらに\(f \in h^A(X)\)であることを利用。(2)から(3)は、\(ψ(u)_X (f) = F(f)(u)\)を利用。(4)から(5)は、\(ψ(u)_Y (gf) = F(gf)(u), g : X \rightarrow Y\)を利用した。
2)\(ψ=φ_{F,A}^{-1}\)である
証明を図6に示す。(3)から(4)へは、\(ψ(u)_A (I_A) = F(I_A) (u)\)を利用した。
3)\(F,A\)に対して自然である。
二つに分け、まず\(A\)に対して自然であることについて考える。
証明に先立って、関手\(h^A\)の性質を復習しておこう。この関手が\(A\)に対して自然であるとき、図7の可換図式を得ることができる。\(f:A \rightarrow B\)のとき、\(h^f : h^B \rightarrow h^A\)と矢印が逆向きになることに注意しておこう。
それでは証明に移る。図8において、真ん中の図が可換図式になればよいので、\(F(f)(φ_{F,A})=φ_{F,X}(N(f))\)が成り立つことを示せばよい。従って、この図の左右にある二つのストリング・ダイアグラムが同値であることを示せばよい。


それでは、最後に\(F\)に対して自然であるについて考える。
先ほどと同様に、図11において、真ん中の図が可換図式になればよいので、\(μ_A (φ_{F,A} ) = φ_{G,A} (M(μ))\)が成り立つことを示せばよい。従って、この図の左右にある二つのストリング・ダイアグラムが同値であることを示せばよい。
ストリング・ダイアグラムを用いての変形を図12に示す。
それでは、細部を見ていこう。(1)から(2)は\(μ_A\)と\(φ_{F,A} \partial\)を切り離し、その間で、\(FA\)が受け渡しされるので、それを明示。(2)から(3)は\(φ_{F,A} \partial =\partial_A I_A\)を利用。(3)から(4)は\(M(μ) \partial_Y =μ_Y\partial_Y\)(図13参考) を利用。(4)から(5)は\( φ_{G,A} M(μ) \partial = M(μ) \partial_A I_A \)を利用。
これで、米田の補題を証明することができた。式を展開しての証明よりは、ストリング・ダイアグラムを用いてのビジュアルな証明の方が理解しやすかったのではと期待しているのだが、読者の方はどうでしたか。
機会があれば、ストリング・ダイアグラムについて再度触れてみたいと思っている。
*1:\(\partial_Y \in Nat(h^A(Y),F(Y) ) \),\(\partial_Y^{\prime} \in Nat(h^X(Y),F(Y) ) \)としたとき、\(N(f) \partial_Y= \partial_Y^{\prime}\)である。図10に示すように、\(h^f(Y) :h^X(Y) \rightarrow h^A(Y), \partial_Y: h^A(Y) \rightarrow F(Y) \)より、\( \partial_Y^{\prime} : h^X (Y) \rightarrow F(Y) = \partial_Y h^f(Y) \)である。従って、\(N(f) \partial = \partial h^f\)となる。