身近な存在としての量子力学（１４）：重ね合わせの内積

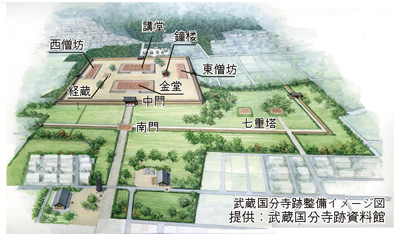
7月に入ってから、世界最古の自筆本日記である『御堂関白記』の読み方を習い始めた。これは、平安時代の貴族、摂政太政大臣・藤原道長（966－1027年）が著した日記だ。2013年にはユネスコ記録遺産にも登録された。995年ごろから書き始めたようだが、998年から1021年までのものが現存している。もともとは、36巻あったそうだが、鎌倉時代の初期に近衛家と九条家に分立するときに二分されたそうで、今日、近衛家の陽明文庫に所蔵されている自筆本14巻が残っている（分立したときは18巻、その後、近衛家から鷹司家へ4巻譲られたようだ）。また、自筆本とは別に、古写本もあるので、失われた部分についてもある程度補われている。

時を同じくして、藤原実資（さねすけ）が『小右記』（977－1040年）を、藤原行成（ゆきなり）が『権記』（991－1011年、なお1026年まで逸文あり）を著しているので、行事や事件に対する見方を比較することができる。

御堂関白記については、2013年に倉本一宏が、『藤原道長の権力と欲望「御堂関白記」を読む』、『藤原道真の日常生活』、『藤原道長「御堂関白記」を読む』の3冊を上梓している。3冊も同時にとはすごい思い入れだなと感心する。

また、これに先立って、2009年に倉本一宏が現代語訳『藤原道長「御堂関白記」全現代語訳』を著している。

藤原道長と同時代に生きていたのが紫式部である。彼女は、藤原道長の娘、彰子（しょうし）に仕えている。彰子は一条天皇の中宮となり、後一条天皇の母である。紫式部は、彰子に仕えている頃に日本最古の長編小説『源氏物語』を著した。

紫式部がこの小説をなぜ書いたのかのなぞ解きを、高山由紀子が小説『源氏物語～千年の謎～」でしている。

本当かどうかは不明だが、藤原道長が光源氏のモデルであるとしている。この小説は映画にもなっていている。映画『千年の恋　光る源氏物語』(2001年）では吉永小百合が、『源氏物語　千年の謎』(2012年）では中谷美紀が紫式部を演じている。前者は艶っぽい古代を、後者は呪われた世界を描き出している。両者とも、バーチャルな世界とリアルな世界が交錯し、奇妙な感じを抱く。

１１．重ね合わせの内積

さて、今回の話題は、ケットとブラを結び付けたらどうなるかを見ていくことにしよう。御堂関白記と源氏物語を融合させたものを見せられた時のような感動には及ばないのだが、それでも、すごいと思う場面である。

１１．１　重ね合わせの内積の原理

1粒子の重ね合わせはケットでは次のように表していた。

\begin{align*}
\hat{\Psi}^\dagger | ...00\dot{0}00...> & = \sum_{i=-\infty}^\infty \psi_i \hat{a}_i^\dagger | ...00\dot{0}00...> \\
& = ... + \psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> + \psi_0 |...00\dot{1}00...> \\
& \ \ + + \psi_1 |...00\dot{0}100...> + \psi_2 |...00\dot{0}0100...> + ...
\end{align*}

また、ブラでは次のように表していた。
\begin{align*}<...00\dot{0}00...|\hat{\Psi} & = <...000\dot{0}00...| \sum_{i=-\infty}^\infty \hat{a}_i \psi_i^* \\
& = ...<...0010\dot{0}00...| \psi_{-2}^* + <...001\dot{0}00...|_{-1} \psi_{-1}^* + <...000\dot{1}00...| \psi_0^*\\
& \ \ + <...00\dot{0}100...|\psi_1^* + <...000\dot{0}0100...| \psi_2^* + ...
\end{align*}

そこで、これらの内積を次のように表すことにしよう。
\begin{align*}
& <...00\dot{0}00...|\hat{\Psi} \hat{\Psi}^\dagger | ...00\dot{0}00..> \\
= & (\sum_{i=-\infty}^\infty \psi_i \hat{a}_i^\dagger | ...00\dot{0}00...>)(<...00\dot{0}00...| \sum_{i=-\infty}^\infty \hat{a}_i \psi_i) \\
= & (...+ <...0010\dot{0}00...| \psi_{-2}^* + <...001\dot{0}00...|\psi_{-1}^* + <...000\dot{1}00...| \psi_0^* + <...00\dot{0}100...|\psi_1^* + <...000\dot{0}0100...| \psi_2^* + ...) \\
& (... + \psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> + \psi_0 |...00\dot{1}00...> + \psi_1 |...00\dot{0}100...> + \psi_2 |...00\dot{0}0100..> + ... )\\
= & ... \\
& + <...0010\dot{0}00...| \psi_{-2}^* (...\psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> + \psi_0 |...00\dot{1}00...> + \psi_1 |...00\dot{0}100...> + \psi_2 |...00\dot{0}0100..> ... ) \\
& + <...001\dot{0}00...| \psi_{-1}^* (...\psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> + \psi_0 |...00\dot{1}00...> + \psi_1 |...00\dot{0}100...> + \psi_2 |...00\dot{0}0100..> ... ) \\
& + <...000\dot{1}00...| \psi_0^* (...\psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> + \psi_0 |...00\dot{1}00...> + \psi_1 |...00\dot{0}100...> + \psi_2 |...00\dot{0}0100..> ... ) \\
& + <...00\dot{0}100...|\psi_1^* (...\psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> + \psi_0 |...00\dot{1}00...> + \psi_1 |...00\dot{0}100...> + \psi_2 |...00\dot{0}0100..> ... ) \\
& + <...00\dot{0}0100...| \psi_2^* (...\psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> + \psi_0 |...00\dot{1}00...> + \psi_1 |...00\dot{0}100...> + \psi_2 |...00\dot{0}0100..> ... ) \\
& + ... \\
= & ... \\
& + (...<...0010\dot{0}00...|\psi_{-2}^* \psi_{-2}|...0010\dot{0}00...> + <...0010\dot{0}00...| \psi_{-2}^* \psi_{-1} |...001\dot{0}00...> + <...0010\dot{0}00...|\psi_{-2}^* \psi_0 |...00\dot{1}00...> + <...0010\dot{0}00...| \psi_{-2}^* \psi_1 |...00\dot{0}100...> + <...0010\dot{0}00...|\psi_{-2}^* \psi_2 |...00\dot{0}0100..> ... ) \\
& + (...<...001\dot{0}00...| \psi_{-1}^* \psi_{-2} |...0010\dot{0}00...> + <...001\dot{0}00...| \psi_{-1}^* \psi_{-1} |...001\dot{0}00...> + <...001\dot{0}00...| \psi_{-1}^* \psi_0 |...00\dot{1}00...> + <...001\dot{0}00...| \psi_{-1}^* \psi_1 |...00\dot{0}100...> + <...001\dot{0}00...|\psi_{-1}^* \psi_2 |...00\dot{0}0100..> ...) \\
& + (...<...000\dot{1}00...| \psi_0^* \psi_{-2} |...0010\dot{0}00...> + <...000\dot{1}00...| \psi_0^* \psi_{-1} |...001\dot{0}00...> + <...000\dot{1}00...| \psi_0^* \psi_0 |...00\dot{1}00...> + <...000\dot{1}00...| \psi_0^* \psi_1 |...00\dot{0}100...> + <...000\dot{1}00...| \psi_0^* \psi_2 |...00\dot{0}0100..> ...) \\
& + (...<...00\dot{0}100...|\psi_1^* \psi_{-2} |...0010\dot{0}00...> + <...00\dot{0}100...|\psi_1^* \psi_{-1} |...001\dot{0}00...> + <...00\dot{0}100...|\psi_1^* \psi_0 |...00\dot{1}00...> + <...00\dot{0}100...|\psi_1^* \psi_1 |...00\dot{0}100...> + <...00\dot{0}100...|\psi_1^* \psi_2 |...00\dot{0}0100..> ...) \\
& + (...<...00\dot{0}0100...| \psi_2^* \psi_{-2} |...0010\dot{0}00...> + <...00\dot{0}0100...| \psi_2^* \psi_{-1} |...001\dot{0}00...> + <...00\dot{0}0100...| \psi_2^* \psi_0 |...00\dot{1}00...> + <...00\dot{0}0100...| \psi_2^* \psi_1 |...00\dot{0}100...> + <...00\dot{0}0100...| \psi_2^* \psi_2 |...00\dot{0}0100..> ...) \\
& + ... \\
= & ... \\
& + (...\psi_{-2}^* \psi_{-2}<...0010\dot{0}00...|...0010\dot{0}00...> + \psi_{-2}^* \psi_{-1}<...0010\dot{0}00...|...001\dot{0}00...> + \psi_{-2}^* \psi_0<...0010\dot{0}00...|...00\dot{1}00...> + \psi_{-2}^* \psi_1<...0010\dot{0}00...|...00\dot{0}100...> + \psi_{-2}^* \psi_2<...0010\dot{0}00...|...00\dot{0}0100..> ... ) \\
& + (...\psi_{-1}^* \psi_{-2}<...001\dot{0}00...|...0010\dot{0}00...> + \psi_{-1}^* \psi_{-1}<...001\dot{0}00...|...001\dot{0}00...> + \psi_{-1}^* \psi_0<...001\dot{0}00...|...00\dot{1}00...> + \psi_{-1}^* \psi_1<...001\dot{0}00...|...00\dot{0}100...> + \psi_{-1}^* \psi_2<...001\dot{0}00...|...00\dot{0}0100..> ...) \\
& + (...\psi_0^* \psi_{-2}<...00\dot{1}00...|...0010\dot{0}00...> + \psi_0^* \psi_{-1}<...00\dot{1}00...|...001\dot{0}00...> + \psi_0^* \psi_0<...00\dot{1}00...|...00\dot{1}00...> + \psi_0^* \psi_1<...00\dot{1}00...|...00\dot{0}100...> + \psi_0^* \psi_2<...00\dot{1}00...|...00\dot{0}0100..> ...) + \\
& + (...\psi_1^* \psi_{-2}<...00\dot{0}100...|...0010\dot{0}00...> + \psi_1^* \psi_{-1}<...00\dot{0}100...|...001\dot{0}00...> + \psi_1^* \psi_0 <...00\dot{0}100...|...00\dot{1}00...> + \psi_1^* \psi_1<...00\dot{0}100...|...00\dot{0}100...> + \psi_1^* \psi_2<...00\dot{0}100...|...00\dot{0}0100..> ...) \\
& + (...\psi_2^* \psi_{-2}<...00\dot{0}0100...|...0010\dot{0}00...> + \psi_2^* \psi_{-1}<...00\dot{0}0100...|...001\dot{0}00...> + \psi_2^* \psi_0<...00\dot{0}0100...|...00\dot{1}00...> + \psi_2^* \psi_1<...00\dot{0}0100...|...00\dot{0}100...> + \psi_2^* \psi_2<...00\dot{0}0100...|...00\dot{0}0100..> ...) \\
& + ... \\
= & ... + \psi_{-2}^* \psi_{-2}+\psi_{-1}^* \psi_{-1}+\psi_{0}^* \psi_{0}+\psi_{1}^* \psi_{1}+\psi_{2}^* \psi_{2} + ...
\end{align*}

いくつか内積を求めてみよう。
\begin{align*}
& <...00\dot{0}00...|\hat{a}_1 \psi_1^* \hat{\Psi}^\dagger | ...00\dot{0}00..> \\
&= \psi_{1}^* \psi_{1}
\end{align*}

別の例を示そう。
\begin{align*}
& <...00\dot{0}00...|\hat{a}_1 \psi_1^* \psi_1 \hat{a}_1^\dagger | ...00\dot{0}00..> \\
&= \psi_{1}^* \psi_{1}
\end{align*}

１１．２　重ね合わせの内積をHaskellで実現する

原理の説明がとても長くなってしまったが、プログラムの方はいたって簡単だ。状態があっているものを抜き出して、複素数で表されたスカラー量を掛け合わせたものの総和を取ればよいので次のようになる。

重ね合わせの内積は^**^で表すことにしよう。プログラムは次のようになる。

infix 4 ^**^
(^**^) :: (Num a, Eq a, Ord a, Show a, RealFloat b, Show b) => CoEntangle a (Complex b) -> Entangle (Complex b) a -> Complex b
(^**^) b k = product b k (0 :+ 0) where
  product EnZero' _ s = s
  product _  EnZero s = s
  product b@(bs :|: (ba, bb)) k@((ka, kb) :&: ks) s
    |ba < kb   = product bs k s 
    |ba > kb   = product b ks s
    |otherwise = product bs ks s + bb * ka

モジュール名はQtm.Entangleとしよう。プログラムの全体を示すと次のようになる。

{-#LANGUAGE GADTs #-}

module Qtm.Entangle (Entangle (EnZero, (:&:)), esort, (+&), prEntangle, normalize, CoEntangle (EnZero', (:|:)), esort', (-|), prCoEntangle, normalize', (^**^))where

import Data.Complex
import Qtm.Entangle.KetEntangle
import Qtm.Entangle.BraEntangle

-- Inner Product of a Bra Entaglement and a Ket Entaglement
infix 4 ^**^
(^**^) :: (Num a, Eq a, Ord a, Show a, RealFloat b, Show b) => CoEntangle a (Complex b) -> Entangle (Complex b) a -> Complex b
(^**^) b k = product b k (0 :+ 0) where
  product EnZero' _ s = s
  product _  EnZero s = s
  product b@(bs :|: (ba, bb)) k@((ka, kb) :&: ks) s
    |ba < kb   = product bs k s 
    |ba > kb   = product b ks s
    |otherwise = product bs ks s + bb * ka

同様にケットとブラの内積も、単独のモジュールKetBraで定義し、次のようにしよう。

{-#LANGUAGE GADTs #-}

module Qtm.KetBra (Ket (KetZero, (:+:)), (+^), (-^), prKet, Bra (BraZero, (:-:)), (^+), (^-), prBra, (^*^), invK, invB)  where

import Qtm.KetBra.Ket
import Qtm.KetBra.Bra

infix 4 ^*^
(^*^) :: (Eq a, Ord a, Num a, Show a) => Bra a -> Ket a -> a
(^*^) b k
  | b == Zero' = 0
  | k == Zero = 0
  | prKet (invB b) == prKet k = 1
  | otherwise = 0

追伸：これまでのプログラム全体をGitHubからダウンロードできるようにしたので、興味ある方は、これを利用するとよい。

また、ケットとブラを利用するときは、モジュールQtm.KetBraを介して利用できる。Braで定義したZero'、また、KetでのZeroは、これまでユーザから見えて気持ち悪かったが、このモジュールを介することで隠蔽された。

身近な存在としての量子力学（１３）：ブラでの重ね合わせをHaskellで表現する

梅雨の中休みの東京の暑さに耐えるのはとても大変だ。昨年までは、7月一杯、運の悪い場合には、8月の第一週まで、講義があったため、ひたすら耐えるしか方法がなかった。しかし、退職した今年は、東京にいる義理はない。そこで、天城高原の別荘に逃げ込んでいる（この記事を書いた七夕の日（木）の日中は東京はなんと36.7度もあったそうだ。東京に戻ってからアップロードしたので、記事は1週間遅れ）。

別荘は、富士山が見えるようにということで、北西に向かって建てられている。午前中は、明るい日差しがベランダに差し込んでいるものの、部屋の中は嘘のように涼しい。爽やかな風が入ってくれば、幸せな気分を味わうこともできる。午後になると日が差し込みだすが、建物の前に立っている大きな杉の木が影を作るので、直射日光を浴びることはない。もし、暑さを感じるようであれば、北面の部屋に逃げ込めばよい。

不便なこともある。標高が700mある山の中にあるので、文明の恩恵を受けることができない。テレビは室内アンテナで受けているので、電波の状況によって映ったりそうでなかったりする。見たいなと思っていた番組が放送されているときに画面が出ないとがっかりする。強力な外部アンテナをつければよいのだが、壁のどこかに穴をあけてアンテナ線を通す工事が必要なので、なかなか踏み切れないでいる。

携帯電話も使えるとは限らない。4Gになることは決してない。アンテナの数が2－3本の3Gの時が多いのだが、それさえ消えそうな時もある。

買い物も大変だ。近くのスーパーまでは15Kmもある。東京だとうんざりする遠さであるが、そこは田舎の良さで、渋滞に巻き込まれることはない。信号も2－3カ所あるだけだ。それでも、毎日、山を下りていくのは億劫なので、まとめ買いになる。

運動不足になっているのではと主治医が詰問しそうだが、大丈夫、朝早く起きて、別荘地内を1時間も歩いている。しかも、上り下りがあるので、東京でのそれと比較すると、決して楽ではない散歩である。別荘地内の家を見るのも楽しみの一つである。なかには、とっても立派な庭を造っているところさえある。

この別荘地は、富士箱根伊豆国立公園の中にあるので、動植物をむやみにとってはいけない。そのおかげで鹿が繁殖しすぎて、被害が進んでいる。鹿はヒイラギの葉は食べないのだが、増えすぎて食べるものが少なくなったのだろう、いつの間にか食べるようになった。シャクナゲもである。昨年あたりから芽と若い葉を食べるようになってきた。せっかく植えたのにこのままでは枯れそうである。鹿が入れないようにするために庭を柵で囲う必要があるのだが、なんとなく自然を壊すようで踏み切れないでいる。

１０．　ブラでの重ね合わせ

さて、ブラをHaskellで表現するところまで進んだ、次は、ブラでの重ね合わせである。

１０．１　ブラでの重ね合わせの原理

ケットでの重ね合わせを復習しよう。ケットでは次のような線形結合を用意した。
\begin{align*}
\hat{\Psi}^\dagger & = ...+\psi_{-2} \hat{a}_{-2}^\dagger + \psi_{-1} \hat{a}_{-1}^\dagger + \psi_0 \hat{a}_0^\dagger + \psi_1 \hat{a}_1^\dagger + \psi_2 \hat{a}_2^\dagger + ... \\
& = \sum_{i=-\infty}^\infty \psi_i \hat{a}_i^\dagger
\end{align*}

そして、1粒子の重なりを次のように定義した。
\begin{align*}
\hat{\Psi}^\dagger | ...00\dot{0}00...> & = \sum_{i=-\infty}^\infty \psi_i \hat{a}_i^\dagger | ...00\dot{0}00...> \\
& = ... + \psi_{-2} |...0010\dot{0}00...> + \psi_{-1} |...001\dot{0}00...> \\
& \ + \psi_0 |...00\dot{1}00...> + \psi_1 |...00\dot{0}100...> \\
& \ + \psi_2 |...00\dot{0}0100..> + ...
\end{align*}

ブラの場合も同じように次のような線形結合を用意しよう。
\begin{align*}
\hat{\Psi} & = ...\hat{a}_{-2} \psi_{-2}^* + \hat{a}_{-1} \psi_{-1}^* + \hat{a}_0 \psi_0^* + \hat{a}_1 \psi_1^* + \hat{a}_2 \psi_2^* + ... \\
& = \sum_{i=-\infty}^\infty \hat{a}_i \psi_i^*
\end{align*}
ここで、\(\psi_{i}\)と\(\psi_{i}^*\)とは共役な複素数（虚数部の符号が反対）である。例えば、\(3+2i\)の共役複素数は\(3-2i\)である。
そして、1粒子の重なりを次のように定義しよう。
\begin{align*}<...00\dot{0}00...|\hat{\Psi} & = <...00\dot{0}00...| \sum_{i=-\infty}^\infty \hat{a}_i \psi_i \\
& = <...00\dot{0}00...|(...\hat{a}_{-2} \psi_{-2}^* + \hat{a}_{-1} \psi_{-1}^* + \hat{a}_0 \psi_0^* + \hat{a}_1\psi_1^* + \hat{a}_2 \psi_2^* + ...) \\
& = ...<...00\dot{0}00...|\hat{a}_{-2} \psi_{-2}^* + <...00\dot{0}00...|\hat{a}_{-1} \psi_{-1}^* \\
& \ \ + <...00\dot{0}00...|\hat{a}_0 \psi_0^* + <...00\dot{0}00...|\hat{a}_1\psi_1^* \\
& \ \ + <...00\dot{0}00...|\hat{a}_2 \psi_2^* + ... \\
& = ... + <...0010\dot{0}00...| \psi_{-2}^* + <...001\dot{0}00...|_{-1} \psi_{-1}^* \\
& \ \ + <...00\dot{1}00...| \psi_0^* + <...00\dot{0}100...|\psi_1^* \\
& \ \ + <...00\dot{0}0100...| \psi_2^* + ...
\end{align*}

１０．２　ブラでの重ね合わせをhaskellで表現する

ケットの重ね合わせを表す型Entangleは次のように定義した。

infixr 5 :&:

data Entangle a b 
  where
    EnZero  :: Entangle a b
    (:&:) :: (a, b) -> Entangle a b -> Entangle a b

同じように、ブラの重ね合わせCoEntangleは次のように定義しよう。

infixl 5 :|:

data CoEntangle a b 
  where
    EnZero'  :: CoEntangle a b
    (:|:) :: CoEntangle a b -> (a, b) -> CoEntangle a b

このデータ型を表示するために、Showを定義しておこう。

instance (Show a, Read a, Eq a, Ord a, Show b, Read b, Eq b) => Show (CoEntangle a b)  where
    showsPrec _ EnZero' = showString ""
    showsPrec n (EnZero' :|: (xa, xb)) = showString "a" . showsPrec n xa . showString "_" . showsPrec n xb
    showsPrec n (x :|: (ya, yb)) = showsPrec n x . showString " + " . showString "a" . showsPrec n ya . showString "_" . showsPrec n yb

また、Eqも定義しておこう。

instance (Eq a, Eq b, Ord b) => Eq (CoEntangle a b)  where
    EnZero' == EnZero'                  = True
    EnZero' == _                        = False
    _ == EnZero'                        = False
    a :|: (ba, bb) == c :|: (da, db) :|: d = (a == c) && (ba == da) && (bb == db)

また、ブラの重ね合わせが左から右に降順になるようにソートする関数esort'を定義しよう。

esort' :: (Eq a, Ord a) => CoEntangle a b -> CoEntangle a b
esort' EnZero' = EnZero'
esort' (xs :|: (xa,xb)) = esort' (larger xs) ||| (EnZero' :|: (xa,xb)) ||| esort' (smaller xs)
    where 
      smaller xs = smaller' xs EnZero'
      smaller' EnZero' s    = s 
      smaller' (ys :|: (ya, yb)) s = if ya < xa then smaller' ys (s :|: (ya, yb)) else smaller' ys s 
      larger xs  = larger' xs EnZero'
      larger'  EnZero' s    = s
      larger'  (ys :|: (ya, yb)) s = if ya >= xa then larger' ys (s :|: (ya, yb)) else larger' ys s

infixl 5 |||
(|||) :: CoEntangle a b -> CoEntangle a b -> CoEntangle a b
(|||) a b = connect a b
    where 
      connect a EnZero' = a
      connect a (xs :|: x) = connect a xs :|: x

また、ブラの重ね合わせが二つあった時に、これを一緒にする関数(-|)を定義しよう。

infixl 5 -|
(-|) :: (Eq a, Ord a, Num b) => CoEntangle a b -> CoEntangle a b -> CoEntangle a b
(-|) x y = esort' $ (-||) (esort' x) (esort' y) EnZero'
    where
      infixl 5 -||
      (-||) :: (Eq a, Ord a, Num b) => CoEntangle a b -> CoEntangle a b -> CoEntangle a b -> CoEntangle a b
      (-||) x EnZero' s = x ||| s
      (-||) EnZero' y s = y ||| s
      (-||) (xs :|: (xa,xb)) (ys :|: (ya,yb)) s
        | xa < ya = (-||) xs (ys :|: (ya,yb)) (s :|: (xa,xb))
        | xa > ya = (-||) (xs :|: (xa,xb)) ys (s :|: (ya,yb))
        | otherwise = (-||) xs ys (s :|: (xa, xb + yb))

ブラの重ね合わせを綺麗にプリントする関数prCoEntangleを用意しよう。

prCoEntangle :: (Show a, Num a, Eq a, Ord a, Show b, Num b) => CoEntangle a b -> String
prCoEntangle EnZero' = ""
prCoEntangle (EnZero' :|: (xa, xb)) = prBra (liftBra xa) ++ show xb
prCoEntangle (y :|: (xa, xb)) =  prCoEntangle y ++ " + " ++ prBra (liftBra xa) ++ show xb

最後に、ブラの重ね合わせを規格化する関数normalize'も用意する。このプログラムでは、複素数が扱えるようにしないといけない。プログラムは少し厄介だが、特に、型シグネチャの部分がてこずるが、次のようにするとよい。なお、このプログラムでは、複素数以外の整数、実数を用いるとエラーになるので、これらを用いたいときは虚数部を0にして使えばよい。例えば、実数3.3を使いたいときは、3.3 :+ 0とすればよい。

normalize'  :: (RealFloat b) => CoEntangle a (Complex b) -> CoEntangle a (Complex b)
normalize' EnZero' = EnZero'
normalize' x = normalize'' x
    where
      total = sqrt $ sum x 0
      sum ::  (RealFloat b) => CoEntangle a (Complex b) -> b -> b
      sum EnZero' s = s
      sum (x :|: (ya, yb)) s = sum x $ (magnitude yb) * (magnitude yb)  + s
      normalize'' EnZero' = EnZero'
      normalize'' (x :|: (ya, yb)) = normalize'' x :|: (ya, (realPart yb) / total :+ (imagPart yb) / total)

liftBra :: a -> Bra a
liftBra a = BraZero :-: a

この部分についてはケットの重ね合わせを規格化する関数も変更しないとならない。それは次のようになる。

normalize  ::  (RealFloat a) => Entangle (Complex a) b -> Entangle (Complex a) b
normalize EnZero = EnZero
normalize x = normalize'' x
    where
      total = sqrt $ sum x 0
      sum ::  (RealFloat a) => Entangle (Complex a) b -> a -> a
      sum EnZero s = s
      sum ((xa, xb) :&: y) s = sum y $ (magnitude xa) * (magnitude xa)  + s
      normalize'' EnZero = EnZero
      normalize'' ((xa, xb) :&: y) = ((realPart xa) / total :+ (imagPart xa) / total, xb) :&: normalize'' y

liftKet :: a -> Ket a
liftKet a = a :+: KetZero

１０．３　プログラムの全体

モジュールの数が増えてきたので、そろそろ階層化して、整理しよう。量子力学に関連するプログラムはQtmの下に置く。
また、ケットとブラにかかわるものは、Qtmの下のKetBraに置くことにする。また、重ね合わせに関するプログラムは、Qtmの下のEntangleに置くことにする。

ブラの重ね合わせのモジュールをQtm.Entangle.BraEntangleとした時のプログラムの全体を示す。なお、このとき、Braのモジュール名は、Qtm.KetBra.Braに変更する。

{-#LANGUAGE GADTs #-}

module Qtm.Entangle.BraEntangle (CoEntangle (EnZero', (:|:)), esort', (-|), prCoEntangle, normalize')  where

import Qtm.KetBra.Bra
import Data.Complex

infixl 5 :|:

data CoEntangle a b 
  where
    EnZero'  :: CoEntangle a b
    (:|:) :: CoEntangle a b -> (a, b) -> CoEntangle a b

esort' :: (Eq a, Ord a) => CoEntangle a b -> CoEntangle a b
esort' EnZero' = EnZero'
esort' (xs :|: (xa,xb)) = esort' (larger xs) ||| (EnZero' :|: (xa,xb)) ||| esort' (smaller xs)
    where 
      smaller xs = smaller' xs EnZero'
      smaller' EnZero' s    = s 
      smaller' (ys :|: (ya, yb)) s = if ya < xa then smaller' ys (s :|: (ya, yb)) else smaller' ys s 
      larger xs  = larger' xs EnZero'
      larger'  EnZero' s    = s
      larger'  (ys :|: (ya, yb)) s = if ya >= xa then larger' ys (s :|: (ya, yb)) else larger' ys s

infixl 5 |||
(|||) :: CoEntangle a b -> CoEntangle a b -> CoEntangle a b
(|||) a b = connect a b
    where 
      connect a EnZero' = a
      connect a (xs :|: x) = connect a xs :|: x

infixl 5 -|
(-|) :: (Eq a, Ord a, Num b) => CoEntangle a b -> CoEntangle a b -> CoEntangle a b
(-|) x y = esort' $ (-||) (esort' x) (esort' y) EnZero'
    where
      infixl 5 -||
      (-||) :: (Eq a, Ord a, Num b) => CoEntangle a b -> CoEntangle a b -> CoEntangle a b -> CoEntangle a b
      (-||) x EnZero' s = x ||| s
      (-||) EnZero' y s = y ||| s
      (-||) (xs :|: (xa,xb)) (ys :|: (ya,yb)) s
        | xa < ya = (-||) xs (ys :|: (ya,yb)) (s :|: (xa,xb))
        | xa > ya = (-||) (xs :|: (xa,xb)) ys (s :|: (ya,yb))
        | otherwise = (-||) xs ys (s :|: (xa, xb + yb))

instance (Eq a, Eq b, Ord b) => Eq (CoEntangle a b)  where
    EnZero' == EnZero'                  = True
    EnZero' == _                        = False
    _ == EnZero'                        = False
    a :|: (ba, bb) == c :|: (da, db) :|: d = (a == c) && (ba == da) && (bb == db)


instance (Show a, Read a, Eq a, Ord a, Show b, Read b, Eq b) => Show (CoEntangle a b)  where
    showsPrec _ EnZero' = showString ""
    showsPrec n (EnZero' :|: (xa, xb)) = showString "a" . showsPrec n xa . showString "_" . showsPrec n xb
    showsPrec n (x :|: (ya, yb)) = showsPrec n x . showString " + " . showString "a" . showsPrec n ya . showString "_" . showsPrec n yb


prCoEntangle :: (Show a, Num a, Eq a, Ord a, Show b, Num b) => CoEntangle a b -> String
prCoEntangle EnZero' = ""
prCoEntangle (EnZero' :|: (xa, xb)) = prBra (liftBra xa) ++ show xb
prCoEntangle (y :|: (xa, xb)) =  prCoEntangle y ++ " + " ++ prBra (liftBra xa) ++ show xb

liftBra :: a -> Bra a
liftBra a = BraZero :-: a

normalize'  :: (RealFloat b) => CoEntangle a (Complex b) -> CoEntangle a (Complex b)
normalize' EnZero' = EnZero'
normalize' x = normalize'' x
    where
      total = sqrt $ sum x 0
      sum ::  (RealFloat b) => CoEntangle a (Complex b) -> b -> b
      sum EnZero' s = s
      sum (x :|: (ya, yb)) s = sum x $ (magnitude yb) * (magnitude yb)  + s
      normalize'' EnZero' = EnZero'
      normalize'' (x :|: (ya, yb)) = normalize'' x :|: (ya, (realPart yb) / total :+ (imagPart yb) / total)

ケットの重ね合わせの方も一部変更したので、全体を示す。なお、モジュール名は、Qtm.Entangle.KetEntangleとしよう。

{-#LANGUAGE GADTs #-}

module Qtm.Entangle.KetEntangle (Entangle (EnZero, (:&:)), esort, (+&), prEntangle, normalize) where

import Qtm.KetBra.Ket
import Data.Complex

infixr 5 :&:

data Entangle a b 
  where
    EnZero  :: Entangle a b
    (:&:) :: (a, b) -> Entangle a b -> Entangle a b

esort :: (Eq b, Ord b) => Entangle a b -> Entangle a b
esort EnZero = EnZero
esort ((xa,xb) :&: xs) = esort (smaller xs) &&& ((xa,xb) :&: EnZero) &&& esort (larger xs)
    where 
      smaller xs = smaller' xs EnZero
      smaller' EnZero s    = s 
      smaller' ((ya, yb) :&: ys) s = if yb < xb then smaller' ys ((ya, yb) :&: s) else smaller' ys s 
      larger xs  = larger' xs EnZero
      larger'  EnZero s    = s
      larger'  ((ya, yb) :&: ys) s = if yb >= xb then larger' ys ((ya, yb) :&: s) else larger' ys s
infixr 5 &&&
(&&&) :: Entangle a b -> Entangle a b -> Entangle a b
(&&&) a b = connect a b
    where 
      connect EnZero b = b
      connect (x :&: xs) b = x :&: connect xs b

infixr 5 +&
(+&) :: (Num a, Eq b, Ord b) => Entangle a b -> Entangle a b -> Entangle a b
(+&) x y = esort $ (+&&) (esort x) (esort y) EnZero
    where
      infixr 5 +&&
      (+&&) :: (Num a, Eq b, Ord b) => Entangle a b -> Entangle a b -> Entangle a b -> Entangle a b
      (+&&) x EnZero s = x &&& s
      (+&&) EnZero y s = y &&& s
      (+&&) ((xa,xb) :&: xs) ((ya,yb) :&: ys) s
        | xb < yb = (+&&) xs ((ya,yb) :&: ys) ((xa,xb) :&: s)
        | xb > yb = (+&&) ((xa,xb) :&: xs) ys ((ya,yb) :&: s)
        | otherwise = (+&&) xs ys ((xa + ya,xb) :&: s)

instance (Eq a, Eq b, Ord b) => Eq (Entangle a b)  where
    EnZero == EnZero                   = True
    EnZero == _                        = False
    _ == EnZero                        = False
    (aa, ab) :&: b == (ca, cb) :&: d = (aa == ca) && (ab == cb) && (b == d)


instance (Show a, Read a, Eq a, Show b, Read b, Eq b, Ord b) => Show (Entangle a b)  where
    showsPrec _ EnZero   = showString ""
    showsPrec n ((xa, xb) :&: EnZero)   = showsPrec n xa . showString "_a" . showsPrec n xb . showString "^"
    showsPrec n ((xa, xb) :&: y)   = showsPrec n xa . showString "_a" . showsPrec n xb . showString "^ + " . showsPrec n y

prEntangle :: (Show a, Num a, Show b, Num b, Eq b, Ord b) => Entangle a b -> String
prEntangle EnZero = ""
prEntangle ((xa, xb) :&: EnZero) = "(" ++ show xa ++ ")" ++ prKet (liftKet xb)
prEntangle ((xa, xb) :&: y) = "(" ++ show xa ++ ")" ++ prKet (liftKet xb) ++ " + " ++ prEntangle y

liftKet :: a -> Ket a
liftKet a = a :+: KetZero

normalize  ::  (RealFloat a) => Entangle (Complex a) b -> Entangle (Complex a) b
normalize EnZero = EnZero
normalize x = normalize'' x
    where
      total = sqrt $ sum x 0
      sum ::  (RealFloat a) => Entangle (Complex a) b -> a -> a
      sum EnZero s = s
      sum ((xa, xb) :&: y) s = sum y $ (magnitude xa) * (magnitude xa)  + s
      normalize'' EnZero = EnZero
      normalize'' ((xa, xb) :&: y) = ((realPart xa) / total :+ (imagPart xa) / total, xb) :&: normalize'' y

ラザーニャ

今年のテニスのウィンブルドン大会は、天候に恵まれず、雨により試合が中断されたり、延期になったりしている。このため、選手は体調の管理が難しそうだが、錦織選手には良い方向に作用しているようだ。ウィンブルドンの前の試合で脇腹を痛め、その影響が出るのではと心配されていた。しかし、連戦になりそうなときに、雨で試合が翌日に順延されたりして、幸運が続いている。現在、三回戦までは無事に勝ち進んでいる。絶対的な強さを誇っているセルビアのジョコビッチ選手が、ビッグサーバーのクエリー選手に敗退した。これで、錦織選手の優勝のチャンスも高まったので、是非、頑張ってほしい。

昨日は、ラザーニャの材料を買いに、近くのモールに出かけた。猛暑に近い日とあって、涼を求めに来ている客が多いのか、沢山の人が買い物に来ていた。特にすごかったのは、レジに並んでいる客の多さである。これまでも、土曜日は特に混んでいることには気がついていたけれども、それでも、各レジに並んでいる客の数は10人程度であった。しかし、昨日は、40人も50人もの客が並んでいた。そのため、レジに進むように作られている陳列棚のそれぞれで、陳列棚一杯にレジ待ちの客さんが並んでいる始末であった。

料理に合った食材を時間をかけて探そうと思っていた小さな夢は、入店した瞬間に打ち砕かれた。レジ待ちの客を押し分けながら、購入品のリストを見ながら、見つかったものから手に取ることになってしまった。特に、ラザニアの生地とミートソースは時間をかけていいものを探したかったのだが、悔いが残った。

ラザーニャは手のかかる料理である。この料理は、ラザニアにミートソース、チーズ、バジルなどを挟み、その全体をホワイトソースで包んで、オーブンレンジで焼き上げる料理である。また、時間のかかる料理でもある。レストランに行ってラザニアを頼むと、かなりの時間待たされるので、避けている人も多いことと思う。時間がかかるのは、ラザニアを茹でる作業である。これに30分程度時間がかかる。今回はこれをさぼることとし、茹でる必要のないラザニアの生地を手に入れた（バリア製）。また、ミートソースも今回は市販のものを利用した。

今日の料理に利用した食材は下の写真のとおりである。

これらの中で、ラザニア(6枚)の間に挟むのが、ミートソース(250g)、エリンギ(70g、2本程度)、モッツアレラチーズ(50g)、バジル(3枚)である。ラザニアを包むようにかけるホワイトソースには、バター(15g)、薄力粉(15g)、牛乳(300cc)、ナツメグ、塩、コショウを使用する。また、パルメザンチーズは全体にまぶして利用する。

それでは、下準備を始めよう。
エリンギは、真ん中あたりで半分に切った後、5cm幅で縦方向に切る。

フライパンにバターを入れて熱し、色づいてきたら、エリンギを並べて両面を焼く。

これをキッチンペーパーの上に置き、油を取る。

モッツアレラチーズは5mm角に切る。

次はホワイトソースに挑戦だ。ダマができないように、細心の注意を払う。鍋にバターを入れ、熱する。溶け終わるころ薄力粉を入れて、ヘラでかき混ぜる。焦げないように気を付けながら、2-3分、滑らかになるまで、かき混ぜる。いったん火を落とし、牛乳を一気に注ぎ込む。また、火を入れて中火で、ダマができないように泡だて器で素早く混ぜる。

トロ味が出てきたところで、火をとめる。ナツメグ、塩、コショウを加えて混ぜる。その後はふたをしておく（表面に膜ができるのを防ぐ）。

準備が整ったので、ラザニアを積んでいこう。耐熱皿に、オリーブオイルを塗りつける。その上にホワイトソースを表面を覆う程度に加える。そして、ラザニアを1枚おく。

ラザニアの上に、ミートソース、エリンギ、モッツアレラチーズ、さらには、バジルの葉を、材料の1/3ほど、この順番で重ねていく（注意しておくことがある。今回購入したミートソースは260gであった。但し、ラザニアの注意書きに多くの水分をラザニアが吸収するので、50ccほど水を足すこととあったので、その通り、ミートソースに水50ccを加えた）。

1段目ができたので、この上にラザニア2枚を置く。そして、先と同様に、材料をのせる。さらにもう一度（3段目）繰り返し、最後に1枚のラザニアをのせる。

積み重なったラザニアの上からホワイトソースをかける。さらに、パルメザンチーズをまぶす。

ラザニアが水分を十分に吸収するまで20分間放置する。その後、オーブンで、250度15分で焼く。食卓はこのようになった。

また、切り分けられたラザーニャは下の写真の通り。レストランで食べるようなおいしい味でした。

今回も、また、川上文代著『イタリア領地・フランス料理の教科書』を参考にした。

身近な存在としての量子力学（１２）：ブラをHaskellで記述する

１０．ブラをHaskellで記述する

それでは、ブラをHaskellで実現することを考える。

１０．１　ブラをデータ型で定義する

ケットと同じように、ブラも代数型データで表すことにしよう。ケットは7章で次のように定義した。

infixr 5 :+:
data Ket a where
  KetZero :: Ket a
  (:+:) :: a -> Ket a -> Ket a

すなわち、真空状態をKetZeroで表した。また、現在の状態に対して、区間\(i\)に1粒子が存在している状態を
i :+: 現在の状態
で表現した。

ブラもこれと同じように表すことにしよう。真空の状態をBraZeroで表すこととする。また、現在の状態に対して、区間\(i\)で1粒子を欲しがっている状態を、
現在の状態 :-: i
で表すことにしよう。

ケットの時は増加の意味を持たせて+を用いたが、ブラの場合には反対に減少と考え-を用いる。

7章では、状態を表していないケットが生じたときは、例外が発生するようにした。即ち、nothing(0)を出力した。しかし、このように定義すると、内積の計算をする時に不備をきたす。そこで、状態を表していないときは、Zero'で表すこととし、これも、ブラのデータ型に含めるようにした。ブラのデータ型は従って次のように定義した（これに伴って、ケットの方も修正し、Zeroを定義する。これは後すぐ述べる）。

infixl 5 :-:
data Bra a where
  Zero' :: Bra a  -- Don't use it when defining a Bra. It is only used when operating Bra data.
  BraZero :: Bra a
  (:-:) :: Bra a -> a -> Bra a

なお、リストを作るための:-:は左の方に結合されていくので、infixlとした。

ケットの方も、状態を表していないときはZeroで表すこととし、次のように変更した。

infixr 5 :+:
data Ket a where
  Zero :: Ket a  -- Don't use it when defining a Ket. It is only used through operatons.
  KetZero :: Ket a
  (:+:) :: a -> Ket a -> Ket a

次に、ブラの型に、等しいかどうかを判定するための関数Eqと、表示するための関数Showを、インスタンスとして実現する必要がある。

関数Eqの方は、現在の状態とその後に続く演算子の並びが等しいかどうかで判定する。従って、演算子の並び方は異なるが、現在の状態にこれらの演算子を施した結果得られる新たな状態で比較していない。そのため、新たな状態が等しい場合でも、現在の状態と演算子の並びが作るリストが異なっている場合には等しくないと判定される。

プログラムは次のようになる。なお、表示の方はケットの場合に少し変更を及ぼし、演算子の間にカンマ(,)が入るようにした。

instance (Eq a, Ord a) => Eq (Bra a)  where
    Zero' == Zero' = True
    Zero' == _    = False
    _     == Zero' = False
    BraZero == BraZero = True
    BraZero == _       = False
    _       == BraZero = False
    (a :-: b) == (c :-: d) = (a == c) && (b == d)

instance (Show a, Read a, Eq a, Ord a) => Show (Bra a)  where
    showsPrec _ Zero'   = showString "0"
    showsPrec _ BraZero   = showString "< ...00(0)00... |"
    showsPrec n (a :-: b)   = showsPrec n a . showString "-a" . showsPrec n b . showString "," 

実行してみよう。

Prelude> :load "Bra.hs"
[1 of 2] Compiling Ket              ( Ket.hs, interpreted )
[2 of 2] Compiling Bra              ( Bra.hs, interpreted )
Ok, modules loaded: Bra, Ket.
*Bra> let a = BraZero
*Bra> let b = a :-: 1
*Bra> let c = b :-: 2
*Bra> let d = a :-: 2 :-: 1
*Bra> a
< ...00(0)00... |
*Bra> b
< ...00(0)00... |-a1,
*Bra> c
< ...00(0)00... |-a1,-a2,
*Bra> d
< ...00(0)00... |-a2,-a1,
*Bra> c == d
False

ケットの方もこれに合わせて変更した。プルグラムを見てみよう。

instance (Eq a, Ord a) => Eq (Ket a)  where
    Zero == Zero = True
    Zero == _    = False
    _    == Zero = False
    KetZero == KetZero = True
    KetZero == _       = False
    _       == KetZero = False
    (a :+: b) == (c :+: d) = (a == c) && (b == d)

instance (Show a, Read a, Eq a, Ord a) => Show (Ket a)  where
    showsPrec _ Zero   = showString "0"
    showsPrec _ KetZero   = showString "| ...00(0)00... >"
    showsPrec n (a :+: b)   = showString ",a" . showsPrec n a . showString "+" . showsPrec n b

ブラが表す状態をきれいに印字したい。すでに、ケットの方が出来上がっているので、これを利用することにする。次のようにすればよい。与えられたブラの状態に対して、その共役となるケットの状態を作成し、状態の中身をそのままにして、ケットの記号をブラのそれに代えればよいので、次のようになる。

prBra  :: (Eq a, Ord a, Num a, Show a) => Bra a -> String
prBra Zero' = "0"
prBra b = "<" ++ c ++ "|"
  where 
    c =  init $ tail $ prKet (invB b) 

実行してみよう。先の続きである。

*Bra> prBra a
"<...000(0)000...|"
*Bra> prBra b
"<...0000(0)1000...|"
*Bra> prBra c
"<...00000(0)11000...|"
*Bra> prBra d
"<...00000(0)11000...|"

なお、PrKetはZeroに対応するために、プログラムの2行目が変更になっている。全体を示すと次のようになる。

prKet :: (Eq a, Ord a, Num a, Show a) => Ket a -> String
prKet Zero = "0"
prKet KetZero = "|...000(0)000...>"
prKet a = "|..." ++ prKet' (ksort' $ ksort a) [] "right" 0 0 ++ "...>"
    where
      prKet' :: (Eq a, Ord a, Num a, Show a) => Ket a -> String -> String -> a -> a -> String
      prKet' KetZero s "left" _ num  = "000" ++ show num ++ s ++ "000" 
      prKet' KetZero s "right" _ num = "000" ++ s ++ show num ++ "000"
      prKet' (a :+: b) s dir index num
        | dir == "right" && index == a    = prKet' b s dir index (num + 1)
        | dir == "right" && index == 0    = prKet' (a :+: b) (s ++ "(" ++ show num ++ ")") "left" (index + 1) 0
        | dir == "right"                  = prKet' (a :+: b) (s ++ show num) "left" (index + 1) 0 
        | dir == "left"  && index == (-a) = prKet' b s dir index (num + 1)
        | otherwise                       = prKet' (a :+: b) (show num ++ s) "right" index 0 

ksort :: Ord a => Ket a -> Ket a
ksort KetZero = KetZero
ksort (x :+: xs) = ksort (smaller xs) +++ (x :+: KetZero) +++ ksort (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if y < x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if y >= x then larger' ys (y :+: s) else larger' ys s

ksort' :: (Num a, Ord a) => Ket a -> Ket a
ksort' KetZero = KetZero
ksort' (x :+: xs) = ksort' (smaller xs) +++ (x :+: KetZero) +++ ksort' (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if abs y < abs x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if abs y >= abs x then larger' ys (y :+: s) else larger' ys s

infixr 5 +++
(+++) :: Ket a -> Ket a -> Ket a
(+++) a b = connect a b
    where 
      connect KetZero b = b
      connect (x :+: xs) b = x :+: connect xs b 

reverse1 :: Ket a -> Ket a
reverse1 x = reverse' x KetZero
    where
      reverse' KetZero s = s
      reverse' (y :+: ys) s = reverse' ys (y :+: s)

ブラの状態の共役はケットの状態であり、ケットの状態の共役はブラの状態であるので、共役を求める関数を用意しよう。ブラの状態の共役を求める関数invBは次のようにしよう。

invB :: (Eq a, Ord a) => Bra a -> Ket a
invB Zero' = Zero
invB BraZero = KetZero
invB (b :-: a)
  | b == BraZero = a :+: KetZero
  | otherwise    = a :+: (invB b) 

逆に、ケットの状態の共役を求める関数invKは次のようになる。

invK :: (Eq a, Ord a) => Ket a -> Bra a
invK Zero = Zero'
invK KetZero = BraZero
invK (a :+: b)
  | b == KetZero = BraZero :-: a
  | otherwise    = (invK b) :-: a

プログラムを実行してみよう。

*Bra> invB a
| ...00(0)00... >
*Bra> invB b
,a1+| ...00(0)00... >
*Bra> invB c
,a2+,a1+| ...00(0)00... >
*Bra> invB d
,a1+,a2+| ...00(0)00... >
*Bra> invK $ invB a
< ...00(0)00... |
*Bra> invK $ invB b
< ...00(0)00... |-a1,
*Bra> invK $ invB c
< ...00(0)00... |-a1,-a2,
*Bra> invK $ invB d
< ...00(0)00... |-a2,-a1,

１０．２　演算子を定義する

演算子には、生成演算子\(\hat{a}_i\)と消滅演算子\(\hat{a}^\dagger_i\)がある。量子力学では、これらの演算子は、ブラにもケットにも作用できるようにしているが、Haskellは型にうるさい言語である。どちらにも適応できるようにすると曖昧さが残るので、ここでは、それぞれの型に対して用意しよう。

ケットでは、生成演算子には+^を、消滅演算子には-^を用意した。また、右側に接続するという意味で^を右側において用いた。

そこで、ブラでは、左側に接続するという意味で^を左側におき、生成演算子には^+を、消滅演算子には^-を用意しよう。プログラムは次のようになる。これらのプログラムは、^-の共役は+^であり、^+の共役は-^であることを利用している。

infixl 5 ^-
(^-) :: (Eq a, Ord a) => Bra a -> a -> Bra a
(^-) Zero' _ = Zero'
(^-) b a = invK $ a :+: (invB b)

infixl 5 ^+
(^+) :: (Eq a, Ord a) => Bra a -> a -> Bra a
(^+) Zero' _ = Zero'
(^+) b a 
  | b' == c = Zero'
  | otherwise = (invK c) 
    where
      b' = invB b
      c = delete a b'
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

プログラムを実行してみよう。

*Bra> let a = BraZero ^- 2
*Bra> let b = BraZero ^- 2 ^- 3
*Bra> let c = BraZero ^- 2 ^- 3 ^+ 2
*Bra> a
< ...00(0)00... |-a2,
*Bra> b
< ...00(0)00... |-a2,-a3,
*Bra> c
< ...00(0)00... |-a3,

ケットの方の演算子は次のように定義される。7章でのプログラムに、Zeroの処理を加えた。

infixr 5 +^
(+^) :: (Eq a, Ord a) =>  a -> Ket a -> Ket a
(+^) _ Zero = Zero
(+^) a b = a :+: b

infixr 5 -^
(-^) :: (Eq a, Ord a) => a -> Ket a -> Ket a
(-^) _ Zero = Zero
(-^) a b
  | b == c = Zero
  | otherwise = c 
    where
      c = delete a b
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

１０．３　内積を定義する

準備が整ったので、内積を定義しよう。あまりにあっけないのでびっくりすることと思う。これはブラの状態とケットの状態が与えられた時、それらを結合したときの値を求めるものだ。一方のブラの状態から共役であるケットの状態を求め、これが他方のケットの状態と一致していれば1をそうでなければ0を出力する。プログラムは次のようになる。

infix 4 ^*^
(^*^) :: (Eq a, Ord a, Num a, Show a) => Bra a -> Ket a -> a
(^*^) b k
  | b == Zero' = 0
  | k == Zero = 0
  | prKet (invB b) == prKet k = 1
  | otherwise = 0

実行してみよう。テスト用のプログラムを用意しておこう。

{-#LANGUAGE GADTs #-}
module Test where
import Bra
a = BraZero ^- 3 ^- 4 ^- 1
b = 3 +^ 1 +^ 4 +^ KetZero
c = BraZero ^- 3 ^- 4 ^- 1 ^+ 2
d = 2 -^ 3 +^ 1 +^ 4 +^ KetZero

Braのモジュールは
module Bra (Bra (Zero', BraZero, (:-:)), (^+), (^-), prBra, (^*^)) と定義した。

それでは実行してみよう。

*Test> a ^*^ b
1
*Test> a ^*^ d
0
*Test> c ^*^ b
0
*Test> c ^*^ d
0

また、\( < ...00\dot000... | \hat{a}^\dagger_1 \hat{a}^\dagger_2 \hat{a}_1 \hat{a}_2 | ...00\dot000... >\)を内積の位置を動かして実行してみよう。

*Test> BraZero ^- 1 ^- 2 ^*^ 1 +^ 2 +^ KetZero 
1
*Test> BraZero ^- 1 ^- 2 ^+ 1 ^*^ 2 +^ KetZero 
1
*Test> BraZero ^- 1 ^- 2 ^+ 1 ^+ 2 ^*^ KetZero 
1
*Test> BraZero ^- 1 ^*^ 2 -^ 1 +^ 2 +^ KetZero 
1
*Test> BraZero ^*^ 1 -^ 2 -^ 1 +^ 2 +^ KetZero 
1

うまく動いていることが分かる。

１０．４　まとめ

これまで説明してきたことを表にまとめると以下のようになる。

	量子力学	ケット	ブラ
真空状態（ケット）	\(|...00\dot000...>\)	KetZero
真空状態（ブラ）	\(<...00\dot000...|\)		BraZero
区間1，2に1粒子(有)	\(|...00\dot01100...>\)	2 :+: 1 :+: KetZero
区間1，2に1粒子(待)	\(<...00\dot01100...|\)		BraZero :-: 1 :-: 2
生成演算子	\(\hat{a}^\dagger_i\)	i +^	^+ i
消滅演算子	\(\hat{a}_i\)	i -^	^- i
生成演算子使用例	\(\hat{a}^\dagger_1|...00\dot000...>\)	i +^ KetZero
生成演算子使用例	\(<...00\dot000...|\hat{a}^\dagger_1\)		BraZero ^+ i
消滅演算子使用例	\(\hat{a}_1|...00\dot000...>\)	1 -^ KetZero
消滅演算子使用例	\(<...00\dot000...|\hat{a}_1\)		BraZero ^- 1
内積		^*^
内積使用例	\(<...00\dot000...|...00\dot000...>\)	BraZero ^*^ KetZero
状態でない	\(0\)	Zero	Zero'

１０．５　プログラム全体

この記事で説明したプログラムの全体を記載しよう。なお、これらのプログラムの開発に要した時間は2時間であった。半日は覚悟していたのだが、短い時間で出来上がり、Haskellの記述能力の高さに感謝している。

Braに関するプログラムは以下のとおりである。

{-#LANGUAGE GADTs #-}

module Bra (Bra (Zero', BraZero, (:-:)), (^+), (^-), prBra, (^*^))  where

import Ket

infixl 5 :-:

data Bra a where
  Zero' :: Bra a  -- Don't use it when defining a Bra. It is only used when operating Bra data.
  BraZero :: Bra a
  (:-:) :: Bra a -> a -> Bra a
--  deriving (Show, Read, Eq, Ord)

invB :: (Eq a, Ord a) => Bra a -> Ket a
invB Zero' = Zero
invB BraZero = KetZero
invB (b :-: a)
  | b == BraZero = a :+: KetZero
  | otherwise    = a :+: (invB b) 

invK :: (Eq a, Ord a) => Ket a -> Bra a
invK Zero = Zero'
invK KetZero = BraZero
invK (a :+: b)
  | b == KetZero = BraZero :-: a
  | otherwise    = (invK b) :-: a

instance (Eq a, Ord a) => Eq (Bra a)  where
    Zero' == Zero' = True
    Zero' == _    = False
    _     == Zero' = False
    BraZero == BraZero = True
    BraZero == _       = False
    _       == BraZero = False
    (a :-: b) == (c :-: d) = (a == c) && (b == d)

instance (Show a, Read a, Eq a, Ord a) => Show (Bra a)  where
    showsPrec _ Zero'   = showString "0"
    showsPrec _ BraZero   = showString "< ...00(0)00... |"
    showsPrec n (a :-: b)   = showsPrec n a . showString "-a" . showsPrec n b . showString "," 

prBra  :: (Eq a, Ord a, Num a, Show a) => Bra a -> String
prBra Zero' = "0"
prBra b = "<" ++ c ++ "|"
  where 
    c =  init $ tail $ prKet (invB b)  

infixl 5 ^-
(^-) :: (Eq a, Ord a) => Bra a -> a -> Bra a
(^-) Zero' _ = Zero'
(^-) b a = invK $ a :+: (invB b)

infixl 5 ^+
(^+) :: (Eq a, Ord a) => Bra a -> a -> Bra a
(^+) Zero' _ = Zero'
(^+) b a 
  | b' == c = Zero'
  | otherwise = (invK c) 
    where
      b' = invB b
      c = delete a b'
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

infix 4 ^*^
(^*^) :: (Eq a, Ord a, Num a, Show a) => Bra a -> Ket a -> a
(^*^) b k
  | b == Zero' = 0
  | k == Zero = 0
  | prKet (invB b) == prKet k = 1
  | otherwise = 0

修正したケットのプログラムは以下のとおりである。

{-#LANGUAGE GADTs #-}

module Ket (Ket (Zero, KetZero, (:+:)), (+^), (-^), prKet) where

infixr 5 :+:
data Ket a where
  Zero :: Ket a  -- Don't use it when defining a Ket. It is only used through operatons.
  KetZero :: Ket a
  (:+:) :: a -> Ket a -> Ket a

infixr 5 +^
(+^) :: (Eq a, Ord a) =>  a -> Ket a -> Ket a
(+^) _ Zero = Zero
(+^) a b = a :+: b

infixr 5 -^
(-^) :: (Eq a, Ord a) => a -> Ket a -> Ket a
(-^) _ Zero = Zero
(-^) a b
  | b == c = Zero
  | otherwise = c 
    where
      c = delete a b
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

instance (Eq a, Ord a) => Eq (Ket a)  where
    Zero == Zero = True
    Zero == _    = False
    _    == Zero = False
    KetZero == KetZero = True
    KetZero == _       = False
    _       == KetZero = False
    (a :+: b) == (c :+: d) = (a == c) && (b == d)

instance (Show a, Read a, Eq a, Ord a) => Show (Ket a)  where
    showsPrec _ Zero   = showString "0"
    showsPrec _ KetZero   = showString "| ...00(0)00... >"
    showsPrec n (a :+: b)   = showString ",a" . showsPrec n a . showString "+" . showsPrec n b

prKet :: (Eq a, Ord a, Num a, Show a) => Ket a -> String
prKet Zero = "0"
prKet KetZero = "|...000(0)000...>"
prKet a = "|..." ++ prKet' (ksort' $ ksort a) [] "right" 0 0 ++ "...>"
    where
      prKet' :: (Eq a, Ord a, Num a, Show a) => Ket a -> String -> String -> a -> a -> String
      prKet' KetZero s "left" _ num  = "000" ++ show num ++ s ++ "000" 
      prKet' KetZero s "right" _ num = "000" ++ s ++ show num ++ "000"
      prKet' (a :+: b) s dir index num
        | dir == "right" && index == a    = prKet' b s dir index (num + 1)
        | dir == "right" && index == 0    = prKet' (a :+: b) (s ++ "(" ++ show num ++ ")") "left" (index + 1) 0
        | dir == "right"                  = prKet' (a :+: b) (s ++ show num) "left" (index + 1) 0 
        | dir == "left"  && index == (-a) = prKet' b s dir index (num + 1)
        | otherwise                       = prKet' (a :+: b) (show num ++ s) "right" index 0 

ksort :: Ord a => Ket a -> Ket a
ksort KetZero = KetZero
ksort (x :+: xs) = ksort (smaller xs) +++ (x :+: KetZero) +++ ksort (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if y < x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if y >= x then larger' ys (y :+: s) else larger' ys s

ksort' :: (Num a, Ord a) => Ket a -> Ket a
ksort' KetZero = KetZero
ksort' (x :+: xs) = ksort' (smaller xs) +++ (x :+: KetZero) +++ ksort' (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if abs y < abs x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if abs y >= abs x then larger' ys (y :+: s) else larger' ys s

infixr 5 +++
(+++) :: Ket a -> Ket a -> Ket a
(+++) a b = connect a b
    where 
      connect KetZero b = b
      connect (x :+: xs) b = x :+: connect xs b 

reverse1 :: Ket a -> Ket a
reverse1 x = reverse' x KetZero
    where
      reverse' KetZero s = s
      reverse' (y :+: ys) s = reverse' ys (y :+: s)

身近な存在としての量子力学（１１）：ブラ

９．ブラ

量子力学の世界にはこれまでに紹介してきたケットの他に、ブラという記法を用いる。そして、ブラとケットをあわせてブラケット記法(bra-ket notation)と呼ばれる。勿論、ブラもケットも量子力学における量子状態を表すための記法である。名前の付け方がしゃれているというのかふざけているというのか、面白い。カッコは英語では、ブラケット(bracket)と呼ぶ。カッコの左側の片割れを用いての記述をブラと呼び、右側のそれをケットという。

おさらいをしよう。ケットでは真空状態を、
\( | ...00 \dot{0} 000...>\)
また、1番目の区間に1粒子がある場合には、
\( | ...00 \dot{0} 100...>\)
1番目の区間と3番目の区間にそれぞれ1粒子ある場合には、
\( | ...00 \dot{0} 10100...>\)
また、3番目の区間に2個の粒子がある場合には、
\( | ...00 \dot{0} 00200...>\)
と表した。

ブラでも、真空状態は次のように表す。
\( < ...00 \dot{0} 000...|\)

ブラとケットは裏返しの世界になっている。何事も反対の世界だ。
1番目の区間に1粒子がある場合は、次のように表す。
\( | ...00 \dot{0} 100...>\)
これは
\(\hat{a}^\dagger_1|...00 \dot{0} 00100...>\)
と同じである。ここで、\(\hat{a}^\dagger_1\)は生成演算子であった。

ブラの世界では消滅演算子\(\hat{a}_1\)が同じ役割をする。即ち、
\(<...00 \dot{0} 000...| \hat{a}_1\)は\(< ...00 \dot{0} 100...|\)と同じである。
となる（ブラの世界では、演算子は右側に置く。すべてを反対にするのだが、粒子の状態を表す場所だけは、ケットと同じように右に昇順である）。ケットが表の世界とするとブラは裏の世界なので、\(<...00 \dot{0} 100...| \)を表の世界の言葉で説明しにくいのだが、1番目の区間で1個の粒子を欲しがっているとでもいうことにしよう。

ブラとケットは結合することができる。真空状態のブラとケットを結合したものを次のように書く。
\( < ...00 \dot{0} 000...|...00 \dot{0} 000...>\)
このとき、真空状態のブラとケットが結合したときの値（内積と専門用語では呼ばれる）を1と定める。

ブラとケットが、全ての区間において、同じ区間で同じ数を有しているとき、ブラとケットの内積を1とする。例えば、ブラの方が1番目の区間だけが1粒子欲しがっていて、ケットの方は同区間だけが1粒子持っているとき、その内積は1である。それは次式の展開のように真空状態の結合に持っていけるためである。
\begin{align*}
&< ...00 \dot{0} 100...|...00 \dot{0} 100...> \\
=&< ...00 \dot{0} 000...|\hat{a}_1 \hat{a}^\dagger_1|...00 \dot{0} 000...> \\
=&< ...00 \dot{0} 000...|...00 \dot{0} 000...>
=&1
\end{align*}

そうでない場合は0とする。例えば、ブラの方が2番目の区間で欲しがっていて、ケットの方には1番目にしかない場合は次のように、真空状態の結合に持っていけない。このため内積は0となる。
\begin{align*}
&< ...00 \dot{0} 010...|...00 \dot{0} 100...> \\
=&< ...00 \dot{0} 000...|\hat{a}_2 \hat{a}^\dagger_1|...00 \dot{0} 000...> \\
=&0
\end{align*}

さて、ブラとケットが共役であると説明した。これと同様に、生成演算子と消滅演算子も共役である。式で表すと次のようになる。なお、共役は\(^\dagger\)で表す。
\begin{align*}
( < ...00 \dot{0} 00... | )^\dagger &= | ...00 \dot{0} 00... > \\
(\hat{a}_i)^\dagger &= \hat{a}^\dagger_i \\
( < ...00 \dot{0} 00... | \hat{a}_i)^\dagger &= \hat{a}^\dagger_i| ...00 \dot{0} 00... > \\
( | ...00 \dot{0} 00... > )^\dagger &= < ...00 \dot{0} 00... | \\
(\hat{a}^\dagger_i)^\dagger &= \hat{a}_i \\
(\hat{a}^\dagger_i | ...00 \dot{0} 00... > )^\dagger &= < ...00 \dot{0} 00... | \hat{a}_i \\
(\hat{a}_i \hat{a}^\dagger_j)^\dagger &= (\hat{a}^\dagger_j)^\dagger (\hat{a}_i)^\dagger \\
&= \hat{a}_j \hat{a}^\dagger_i \\
(\hat{a}^\dagger_i \hat{a}_j)^\dagger &= (\hat{a}_j)^\dagger (\hat{a}^\dagger_i)^\dagger \\
&= \hat{a}^\dagger_j \hat{a}_i
\end{align*}

なお、
\begin{align*}
\hat{a}^\dagger_i \hat{a}^\dagger_j &= \hat{a}^\dagger_j \hat{a}^\dagger_i \\
\hat{a}_i \hat{a}_j &= \hat{a}_j \hat{a}_i
\end{align*}

これより、次のことが分かる。
\( < ...00 \dot{0} 1100...|...00 \dot{0} 1100...> \)は\( < ...00 \dot{0} 00...|\hat{a}_1 \hat{a}_2 \hat{a}^\dagger_2 \hat{a}^\dagger_1|...00 \dot{0} 00...> \)とも、\( < ...00 \dot{0} 00...|\hat{a}_2 \hat{a}_1 \hat{a}^\dagger_2 \hat{a}^\dagger_1|...00 \dot{0} 00...> \)とも表すことができる。
前者の場合は、すぐに、\( < ...00 \dot{0} 1100...|...00 \dot{0} 1100...> \)となることが分かるが、後者の場合には、\(\hat{a}_1\)と\(\hat{a}_2\)が入れ替えられることを利用して、次のように式を展開できることでわかる。
\begin{align*}
& < ...00 \dot{0} 00...|\hat{a}_2 \hat{a}_1 \hat{a}^\dagger_2 \hat{a}^\dagger_1|...00 \dot{0} 00...> \\
=& < ...00 \dot{0} 00...|\hat{a}_1 \hat{a}_2 \hat{a}^\dagger_2 \hat{a}^\dagger_1|...00 \dot{0} 00...> \\
=& < ...00 \dot{0} 00...|\hat{a}_1 \hat{a}^\dagger_1|...00 \dot{0} 00...> \\
=& < ...00 \dot{0} 00...|...00 \dot{0} 00...> \\
=& 1
\end{align*}

それでは、これらの概念をHaskellで表現することを次に考えよう。

武蔵国の国分寺跡を訪ねる

昨日（6月29日）の夜は、国分寺でワインを楽しむ会があったので、夕方、国分寺跡を訪ねてみた。

5年近く前になるが、社会科を教えてくださった恩師の先生に伴われて、中学時代の仲間たちと訪れたことがあるが、その時は散策とおしゃべりを楽しむことに費やしてしまった。

今年になって、古代史を勉強し始めた。書物を読んでいるだけではつまらないので、実際のものを見たほうがもっと楽しいだろうと思っていた。そうこうしているうちに、国分寺巡りをしている人に会いましたよという話を先週聞いた。全国には70を超える国分寺があるので、全てを訪問することは大変なことである。近いところのいくつかをと思って、手始めに、武蔵国の国分寺・国分尼寺を訪ねることにした。

国分寺・国分尼寺は、聖武天皇の詔(741年)によって、一国一寺が建てられた。当時は、奈良時代の中頃で、律令制が引かれ、地方行政区画として五畿七道が定められていた。これを説明したホームページには、下図がある。

上の図から分かるように、武蔵国は、最初の頃は、武蔵国は、東海道ではなく、東山道に属していた。そのため、国分寺には、東山道の名残もあるので、ついでに訪れることにした。

国分寺・国分尼寺は、国分寺駅よりは、西国分寺駅の方が近い。下の図で、下の真ん中あたり、武蔵野線を挟んで左側に、黒鐘公園とあるが、このあたりが国分尼寺の跡である。また、右側に、国分寺緑地とあるがこのあたりが国分寺の跡である。

地図をもう少し大きくすると国分寺・国分尼寺の跡がはっきりする。左下が国分尼寺、右上がが国分寺の跡である。

まずは、国分寺跡を訪ねてみる。東京都教育委員会のホームページを見ると、下図のような伽藍になっていたと想定されている。奈良の東大寺と同じ形式で、南北一直線にならば、南から、南門、中門、金堂、講堂が並んでいた。また、金堂から東の方に七重塔があった。

さて、現地の写真だが、金堂の跡には下図のような石碑が立っている。

周囲は次のようになっている。金堂を作った礎石が残され、夏草の中に埋もれそうになっていた。

次は講堂の跡だ。

講堂の跡も夏草に埋もれかけている。礎石を強調したのが下図だ。丸くてしっかりした石だ。

この近くに、国分寺跡の説明もあった。

次は、国分尼寺だ。国分寺と同様に、南門、中門、金堂、講堂、そして、女坊で構成されていたと推察されている。このうち発見されているのは、金堂と女坊である。

金堂跡は次のようになっていた。

女坊と思われる辺りは次のようになっていた。

また、近くには東山道の跡も残されている。

Google Mapで東山道を見ると、その偉大さが分かる。下図で、右端の上半分の茶色い道が東山道武蔵路である。道幅が12m（4車線の道路と同じ）もあったそうである。路づくりのためにたくさんの人が駆り出されたことが想像される。

そして、奈良の都から、武蔵国の国司へ、国書を携えての使いは、左手に国分寺を右手に国分寺尼寺を見て、府中へと向かったのだろう。

追

現在の国分寺は、国分寺跡の奥（北東の位置）にある。遺跡の方から北に向かって進むと、まず、楼門に出くわす。

さらに進むと、本堂が現れてくる。

門をくぐると、左右に万葉集にちなんだ植物が植えられている。

また、門の前を左側（東側）に折れると、お鷹の道である。江戸時代はこの辺りは尾張徳川藩の御鷹場だったそうで、ハケ（崖を表す古語、武蔵野台地には国分寺崖線、立川崖線などがある）の湧水が作る清流に沿って散歩コースがある。

また、右手（西側）に行くと、薬師堂があり、そこには、新田義貞が寄進したとされる木造薬師如来坐像があるが、今回は訪問しなかった。

カポナータ：シチリア風揚げナスの甘酢煮

昨日は、シチリアの代表的な料理であるカポナータを料理した。カポナータは、日本流に説明すると、揚げナスの甘酢煮である。甘酢煮には、酢と砂糖および塩が用いられる。酢の起源を調べてみよう。

日本料理で用いる酢は米を原料としている。米を原料にして醸造酒を作り、そこに酢酸菌を加え、酢酸発酵させることで酢は作られる。ウィキペディアによれば、酢は応神天皇（15代）の頃に中国から渡来したと記載されているが、本当かなと疑問に思う。

天皇という称号は、天武天皇（40代、7世紀）から使われるようになった。このため、応神天皇という呼び名は後の時代になって付けられたものである。あるいは、応神天皇という存在そのものが後から創作された可能性もある。

実在していれば、諡号（しごう）が使われたものと思われる。応神天皇の諡号（しごう）は、日本書紀（720年完成）には「ほむたのすめらみこと」と、また、古事記（712年に元明天皇に献上）には「ほむだわけのみこと」と表記されている。

天皇系譜図の始まりの頃の天皇は実在したかどうか怪しいのだが、応神天皇については、井上光貞が『日本の歴史　第1巻　神話から歴史へ』中公文庫(1964年)で、確実に実在が認められる最初の天皇と記載している。現在の学説がどのようになっているかは知りたいところである。ウィキペディアから御影を借用する。

実在していたとしても、その当時の豪族の一人だと思われる。中国の六朝時代の史書には、倭の5王（5世紀）の記載があり、これらの王が当時の中国の、東晋、栄へ使いを送ったという記載がある。もし、応神天皇がこの時代の豪族の一人であれば、中国に使者を送り、中国の物産や文化をもちこんだ可能性はあるのだが、このことは憶測の域を出ない。

大化の改新(646年)の頃に律令制がひかれ、長い年月をかけてこの制度は完成される。この制度の下に、酒造司（みきのつかさ/さけのつかさ）という役所が置かれ、ここは酒、醴（あまざけ）、酢などの醸造をつかさどっていた。従って、律令制が始まったころ、あるいは完成までの途中の段階では、酢はすでに使われていたことが分かる。

一方、イタリア料理に用いるのは、ブドウを原料にした酢だ。ブドウ液を酢酸発酵させたバルサミコ酢、ワインを酢酸発酵させたワインビネガーがある。ワインには白と赤があるように、ワインビネガーにも白と赤がある。白の方がよくつかわれていると思うが、今回、用いるのは赤の方である。ウィキペディアからこれらの酢の写真を借用する。

ビネガーの歴史を調べようと思って、英語版のWikipediaを検索した。しかし、残念なことにたった一行しか書いてない。「ビネガーは何千年も前から作られ使われ、紀元前3000年のエジプトまでたどれる」となっている。人々の生活に古くから根付いていたのだろう。

歴史探索はこのくらいにして、カポナータを作ってみよう。今回のカポナータは甘酢づくりに凝ってみた。

ナスは米ナスを用いた。アメリカに留学した頃、スーパーで見かけるナスの大きさに仰天させられた。米ナスはそれとは異なるが、アメリカのブラックビューティーという品種を日本で改良したものだ。やはり、群を抜いて大きい。

米ナスは肉質が固いので、加熱して食べる食材で、田楽やグラタンに使われる。また、トマトとの相性も良いので、今回のカポナータ、あるいは、ラタトゥイユにも使われるとのことである。

今日用いる材料は、ナス以外はすべて甘酢を作るための材料だ。玉ねぎ(25g)、セロリ(10g)、松の実(大匙半分)、ケイパー(大匙半分)、グリーンオリーブ(3個)、赤ワインビネガー(15cc)、白ワイン(15cc)、グラニュー糖(小匙半分)、ニンニクオイル(大匙一杯)、イタリアンパセリ、塩、コショウ、トマトソース(100cc)だ。

まず、ナスの方だが、甘酢を作る前に下ごしらえしておく。
2cm角になすを切る（今回は失敗した。次回からは次のように切ろうと思っている。なすを縦方向において、その中心線から左右1cmのところで縦に切る。さらに、それぞれから2cm離れたところでやはり縦に切る。90度回転させて同じように切る。これで、縦方向に2cmの長い材料が得られたので、今度は、切ってある方向とは直角に、即ち、横方向に、2cmずつ切る）。

今度はナスのあく抜きだ。ナスに小匙半分の塩をまぶし、30分間放置する。ナスから水分が出てくるので、水をかけて塩とともに洗い流す。次にナプキンでナスについている水をふき取る。水が残っていると油の中に入れたときに飛び跳ねるので、きれいにふき取ることが大切である。

次に、甘酢を作ろう。グリーンオリーブは種を取り3mm角に切る。セロリ（茎の固い部分はそいで除く）、玉ねぎはみじん切りにする。

次に炒めるがその時ニンニクオイルを用いる。ニンニクオイルは、100ccのエクストラバージンオイルに、5片(50g)ほどのみじん切りにしたニンニクをつけたものである。イタリア料理を作るときは、頻繁に用いるので作っておくと便利である。

フライパンでニンニクオイルをブクブクいうまで熱し、その後、弱火にして松の実を加え、少し色ずくまで炒める。

さらに、ためねぎとセロリをくわえ、甘い香りがするまで炒める。

次に、グリーンオリーブ、ケイパーを入れてざっと炒め、さらに、赤ワインビネガーと白ワインを入れる。きついビネガーの香りがする。好きな人は顔を近づけてもよいが、僕は顔を背けて炒めた。アルコールが飛んだところで、中火にし、トマトソース、塩、コショウを加える。

さて、ナスを揚げて甘酢に絡めよう。ナスは、220度に熱したサラダ油で、少し色がつく程度に揚げた。

これを先ほどの甘酢に絡めた。最後に、グラニュー糖を混ぜてほんの少しだけ甘みを加えた。

昨日の食卓は、妻の手による鶏肉の白ワイン蒸しとともに味わった。なお、カポタータには西洋パセリをのせた。カポナータはなかなか深みのある味であった。

最後に、カポナータを料理するにあたっては、川上文代著『イタリア領地・フランス料理の教科書』を参考にした。

イサキの香草焼き

お魚屋さんにイサキが丸ごとあったので、昨日（6月26日）はこれを料理した。料理の手間を省くために、内臓と鱗を取り除いてもらった。イサキをローストするとき、一緒に、ジャガイモと紫玉ねぎも使うことにした。

従って、今日の香草焼きに用いる食材は、イサキ(1匹)、ジャガイモ(2個小粒であれば3個)、紫玉ねぎ(1個)、魚の臭みを取るために、タイム、ローリエの葉、ローズマリーを用いた。また、ローストした魚を、バジルペースト、レモンに付けて食べる。バジルペーストを作るために、バジルの葉(30g)、ニンニク(5g)、松の実(20g)、パルメザンチーズ(20g)、エクストラバージンオイル(80cc)を用意した。さらに、さらに、ローストするときに、塩とコショウとエクストラバージンオイル(大匙2杯)で味付けを行う。オリーブの実は付け出しで出すことにし、今日の食材は次のようになった（なお、バジルは写真の倍使いました）。

最初に、バジルペーストを作る。これは、バジルの葉、ニンニク、松の実、パルメザンチーズ、エクストラバージンオイルをミキサーにかければよい。

ジャガイモはなかなか火が通らないので、あらかじめ、電子レンジで蒸した。

イサキは、胴体に包丁で左右にそれぞれ2か所ずつ切り込みを入れ、そこに、タイム、ローリエの葉、ローズマリーを詰め込んだ。さらには、お腹にも同様に詰め込んだ。

オーブン皿の上にイサキ、半分に切ったジャガイモ、横にスライスした玉ねぎをのせ、塩とコショウとオリーブオイルかけ、220度で予熱したオーブンで20分間焼いた。

食卓はこのような感じ。

素朴な味でしたが、おいしくいただきました。

真鯛とサーモンのカルパッチョ

うんざりする梅雨のこの季節、食べ物ぐらいは美味しいものを食べたい。そこで、白ワインに合いそうなカルパッチョを作ってみることにした。鯛を丸ごと仕入れてと思って、近くのスーパーに出かけたのだが、残念なことに、見つけることができなかった。仕方なく、お刺身用に下ごしらえしてある真鯛の柵と刺身にされたアトランティックサーモンを購入した。

今日の料理に使うのは、真鯛、サーモン、グレープフルーツ、ルッコラである。また、ドレッシング用に、パプリカ(15g)、キュウリ(10g)、セロリ(10g)、グリーンオリーブ（1粒）である。その他に、塩、コショウ、白ワイン・ビネガー、エクストラバージンオイルである。

まずは、真鯛とサーモンは薄切りにして、お皿一杯に配置する。そして、塩、コショウを少々振りかける。

次にドレッシングを作る。まず、パプリカ、キュウリ、セロリ、グリーンオリーブ（種を取る）を3mm角に切る。オリーブオイル大さじ2杯、白ワイン・ビネガー大さじ1杯、さらに、グレープフルーツの汁大さじ1杯をボールに入れる。先ほど切ったパプリカ、キュウリ、セロリ、グリーンオリーブをボールにくわえ、塩、コショウをボールに加えて、かき混ぜる。

真鯛とサーモンの上に、ドレッシングを均等にかけ、グレープフルーツ（半分）の果肉とルッコラをのせる。とても、簡単なので、あっという間に出来上がる。

食卓は、スープ、サラダ、生ハムを加えて、こんな感じになった。

グレープフルーツは久しぶりに利用したのだが、もう少し、酸味があるかと予想していたのだが、随分と甘くなっているのに驚いた。

伊豆：グランイルミ

北海道から伊豆に戻って、グランパル公園の近くを走っているときに、きれいなイルミネーションがあることに気がついた。妻によると、グランイルミの一部が見えているのだろうということだった。グランパル公園の周りは頻繁に通っているのだが、昼間のことが多く、気がつかなかった。妻から行ってみたいともいわれていたので、小雨が降っていたが、鑑賞することとした。

6月8日の夜7時に入場した。切符を買おうとしたら、あたりに観光客はおらず、我々の姿を見つけた切符売りの人が受付に戻ろうとしている姿を見て、さらに、入場券が1200円と書かれているのを見て、一瞬躊躇した。しかし、まあ、一度ぐらいグランバル公園を見ておくのもよいかなという気分が勝り、二人分の2400円を妻が受付に出した。そしたら、半額になりましたのでと言われ、気分良く入場した。門を潜り抜けた瞬間、そのすごさに圧倒された。いくつかの写真をお見せしよう。

古い街、小樽を訪ねる

6月6日（月）に増毛を後にして、小樽に向かった。増毛から留萌までは、国稀酒造の方に車で送ってもらい、留萌から深川を経由して札幌までローカル線の旅を楽しんだ。札幌でレンタカーを借りて、余市へと向かった。余市は、一昨年の秋から始まったNHKの朝ドラ『マッサン』で有名になった場所である。マッサンが創業したニッカウィスキーの酒造所を訪れてみた。
入り口から入ってすぐのところはこのような感じである。

マッサンがこだわった蒸溜釜も見ることができた。

マッサンが奥さんのリタと住んでいた家の外観も写真に撮った（柱が外側に曲がって見えるのは魚眼レンズで撮影したため。以下の写真も同じである）。

この後、積丹半島を少し見た後で、小樽に向かい夕飯を取った。八角の刺身、

柳の舞（右斜め上）の刺身、

さらには、ナメタガレイのから揚げなど、地元でしか食べられない魚を楽しんだ。

次の日は、運河をクルージングした。その時、船長が小樽の観光客の推移を教えてくれた。往時は900万人の観光客があったが、最近は750万人に減って、しかも、そのうちの半数が中国人であると案内していた。最盛期であった頃はほとんどが日本人であっただろうから、日本人の観光客の落ち込みが著しいのではと想像した。

真偽を確認するために、小樽市のホームページから観光客の推移を追ってみた。このホームページでは、入込客という普段用いない言葉が使われている。入込客は、観光地や遊園地などの施設、観光地域などの入場者数、来訪者数を指す専門用語で、自治体などが地域を訪れた観光客数を「観光入込客数」と表現するそうである。

小樽市を訪れた人の1960年（昭和35年）からの人数の推移を折れ線グラフで示すと以下のようになる。

目立つのは、1998年の666万人から1999年の973万人への異常とも思える増加である。この要因は、1999年3月に開業した小樽マイカルの開業であろう。ホテル、ショッピングセンターを含む巨大な複合施設で、開業1年後に訪問した時には、その大きさにびっくり仰天した。北海道最大の複合施設に道内の人をはじめとして多くの人が訪れ、バブル状態が作り出されたものと思われる。私が行った1年後には、早くもショッピングセンターは寂しい状態になっていた。案の定、小樽マイカルは2001年9月には破産となる。

次に気が付くのは、1986年から1999年にかけて着実に観光客の数が増えていることであろう。これは、1986年に運河の一部が埋め立てられ、道路と平行して散策路が設けられたことで、観光地としての環境が整い、レトロな運河を訪問してみようという機運が高まったことに起因している。

1999年以降は2011年の東日本大震災まで、観光客は減り続ける。小樽マイカルのバブルがはじけたことも大きく起因しているものと思われる。しかし、2011年を境にして、観光客の数が増え始めるので、これは、船頭さんが教えてくれた外国人客の増加によるものと思われる。そこで、統計データを探したのだが、外国人観光客の訪問者数は統計データにはない。そこで、仕方がないので、道内、道外からの入込客数と外国人の宿泊者の数を利用する。

このデータを見ると、近年では道外からの客数が伸びていることが分かる（道外からのかなりの部分は外国人なのだろう。また、道内の中にも含まれていると想像できる）。また、外国人の宿泊者の数だけの折れ線グラフでは以下のようになる。

グラフから、東日本大震災の後、外国人宿泊者が急増していることが分かる。小樽の事情に詳しい人によれば、外国人のほとんどの人は、小樽には宿泊せず、札幌に宿泊するということなので、宿泊者の数は訪問者の数と比較するととても小さくなっているものと想像できる。しかし、宿泊者数と訪問者数の増加の傾向は似ているだろうから、外国人の訪問者は、これと同じような傾向で増えているものと思われる（本来は、統計処理をして確認する必要があるが、ここでは省くこととする）。

現に、小樽の町を歩いていると、日本語よりも中国語の方をよく聞くので、少なくとも、訪問者の半数は中国人と想像できる。従って、船頭さんが言ったことは嘘ではなさそうである。これまでにはなかった事態がここ小樽でも進行しているのだと改めて認識させられた。

少し疲れたので、小樽の町の古い建物を見学することにしよう。最初は、日本銀行小樽支店

次は、三井物産小樽支店

さらに、三菱銀行小樽支店

今はなくなってしまった北海道銀行本店（現在の北海道銀行とは別）

今はホテルとなっている北海道拓殖銀行小樽支店

変わったところで、手宮線の跡地

その他にもたくさんある。これらは、小樽市のホームページを参考にするとよい。

北海道・増毛にうに鍋を食べに行く

6月5日に北海道の増毛に「うに」を食べにいった。

増毛は、「ぞうもう」ではなく、「ましけ」と呼ぶ。アイヌ語で「かもめの多いところ」をマシュキニあるいはマシュケというそうだが、それが転じて「ましけ」になったそうである。

留萌本線の終点の「増毛駅」である。この駅は1921年（大正10年）11月5日に開業した。手元にある大正14年4月号の汽車時間表によると、深川増毛間には、上り列車が6：55、10：25、15：20に増毛を出発、下り電車は9：20、14：30、20：45に増毛に到着する。深川までは3時間かかっている。

東京・大阪間に新幹線が開業した昭和39年10月の時刻表では、深川・増毛間に「かむい」と呼ばれる準急列車が走っている。上りは6：26に増毛を出発、下りは22：31に増毛に到着する。所要時間は1時間20分程度である。

本線となっているので、かつては重要な路線だったのだろうが、今年（2016年）の12月5日に留萌・増毛間の廃止が予定されている。これから廃止までの時期は鉄道ファンが押し寄せて、かつての賑わいをほんの一瞬だけ取り戻すことになるだろう。

現在の増毛駅の写真をいくつか掲載しよう（なお、以下の写真は魚眼レンズで撮ったので、周辺は丸みを帯びている）。

列車は一両編成の気動車だ。

線路の先は、暴走を止められるように、列車止めが設けられている。

増毛駅の駅前には、建物それ自体の重みにやっと耐えているような旅館「富田屋」がある。昭和8年に建てられたそうだが、ニシン漁が盛んだったころ、沢山の人でごった返した所であろう。

旅行をする数か月前に高倉健主演の駅Stationを偶然に鑑賞した。この映画でのロケ地に増毛が使われた。また、富田屋の右隣りの風待食堂も映画では重要な場所である。

向かった先は、「寿司のまつくら」だ。このお店の写真も、また、料理の写真を撮るのも忘れて、「うに料理」を楽しんだ（まつくらを紹介している動画はいくつかあるのでそちらを参考に）。この時期を選んだのは、うにが最高に美味しいからであることは言うまでもない。特に、「うに鍋」は絶品である。うにをふんだんに用いて、あわび、ごぼう、ねぎ、わかめで味付けしてあり、至福の時間を与えてくれる。

増毛は日の入りがきれいなところだ。この日はあいにく雲がかかっていたが、それでも、食事を中断して、日の入りを観察しに出てみた。

雲の切れ目から沈む太陽を見ることができた。

宿泊先のホテルから次の日に見た暑寒別岳の上の方はまだ雪を抱いていた。

増毛で食事を共にしたのは、国稀酒造の方である。国稀は、日本で最北の造り酒屋である（東京でも靖国神社前の天ぷら屋「もも瀬」では、ここのお酒を楽しむことができる）。国稀酒造は明治15年の創業で、創業者は本間泰蔵である。彼は、新潟県の佐渡の生まれで、明治6年小樽に渡り、呉服店の養子格の番頭として働き、ニシン漁で沸き立つ増毛には行商で来ていたとのことである。明治15年に「丸一本間」を名乗り、本業の呉服屋の他に、海運業、ニシン業、そして、醸造業を始めたそうだ。この当時の本店は、現在では、旧商家丸一本間家として、国指定の重要文化財になっており、見学することができる。

酒の名前も当初は「国の誉」であったそうだが、乃木希典の名前にちなんで、大正9年より、国稀という名が使われるようになった（希をそのまま使うのは恐れ多いので、のぎへんを付けたとのことである）。日露戦争の戦没者を弔う慰霊碑の揮毫を乃木希典に依頼したことからつながりができたとのことである。

もう少し、増毛の逸話を挙げることにしよう。前にも出てきたが、この町はニシン漁で栄えたところである。なかにし礼の小説「兄弟」にも出てくるが、ニシン漁は、当たれば大儲けをするし当たらなければ大損をするという、博打の世界でもある。

ニシン漁が最盛期の頃には、ニシン御殿と呼ばれるものがあちらこちらに建てられたが、その名残が、留萌の北の小平（おびら）町にある。旧花田家番屋である。

ニシンの運搬は、重労働であったと思われる。背負子にたくさんのニシンを詰めて、漁船から加工場まで運んだのであろう。

この後、国稀酒造の創業者が最初に北海道で仕事を始めた地、小樽へと向かう。

身近な存在としての量子力学（１０）：重ね合わせ（続き）

８．重ね合わせ（続き）

最近、日本の古代史を学び始めた。殆どの時間をこの時代のことを記述した書籍を読む時間にあてているのだが、若いころの様にはすっと頭の中に入ってこない。特に、諱（いみな）や諡号（しごう）にはてこずる。現存する天皇家の初代の天皇は、越の国（こしのくに）から来た継体天皇とされているが、諱は男大迹（ヲホド）である。見かけない漢字が出てきて戸惑う。

その後を継いだ欽明天皇の漢風諡号は、天国排開広庭である。知っている漢字ばかりだが、読み方が全く分からない。なんと、和風諡号では「あめくにおしはらきひろにわ」と読む。

倉本一宏著「蘇我氏―古代豪族の興亡」では、天皇は諡号で記載されている。初出では、漢風と和風の諡号が両方記載されているが、その次からは漢風諡号だけになる。名前が出てくる度毎に、和風諡号で読もうとするため、思い出すのにたくさんの時間がとられ、読むスピードが一挙に落ちる。さらに悪いことに、和風諡号の読み出し回路を駆使していると文脈も忘れてしまう。そのため、何度も何度も同じところを読むということが繰り返される。

それでも、よいこともある。欽明天皇は、蘇我稲目の娘を妃にする。その当時は、通い婚で、男が女の家に通う。そして、通う先に姉妹がいた場合には、そこにも通わなければならない。蘇我稲目には、堅塩媛（きたしひめ）と小姉君（おあねのきみ）の二人の娘がいたので、欽明天皇はこの二人を妃とした。二人の妃の中が平穏でなかったことは容易に想像できる。そのあたりの事情を小説にしたのが、永井路子の「冬の夜、じいの物語」である。この話は短編なので、「裸足の皇女」の中に含まれている。蘇我氏が勢力を広め始めたころの経緯を知っていると思い出話を聞くようにこの短編を楽しく読むことができる。

それでは話を元に戻そう。前回は、量子力学での重ね合わせをブラを用いた線形結合でどのように表現できるかを説明した。さらに、演算子と状態の空間に分け、演算子の空間だけで、重ね合わせを表現できることを説明した。そして、ヒントを与えて、Haskellでの表現を考えてもらった。今回は、Haskellでどのように表したらよいかを説明しよう。

８．４　重ね合わせをHaskellで表現する

前回の記事で、次の図を説明なしに示した。

今回はこの図を説明した後で、Haskellでの表現を考えることにしよう。図の右側は、普通に使われている重ね合わせの状態（この集りをエンタングル状態空間と呼ぶことにする）をHaskellでの表現に変えたものである。
前の記事で説明したように、重ね合わせの状態は、
\(\Psi=...\psi_{-2}|...00010\dot{0}000...>+\psi_{-1}|...0001\dot{0}000...>+\psi_{0}|...000\dot{1}000...>\)
\(+\psi_{1}|...000\dot{0}1000...>+\psi_{2}|...000\dot{0}01000...>...\)
であった。即ち、\(\psi_{i}\)と\(|...000(0)0...010...>\)(この時、1の位置は\(i\)番目の壱である）を対とした線形結合になっている。そこで、\(\psi_{i}=0\)であるものを除いて、これらの対のリスト、即ち、\([(\psi,a)]\)で表すこととする。

例えば、\(\Psi=\psi_1|...0(0)10...>+\psi_2|...0(0)010...>\)であれば、図のように\([(\psi_1,|...0(0)10...>),(\psi_2,|...0(0)010...>)]\)と表す。

しかし、この表現は、状態が無限の長さの数字の列にあっているため、Haskellの中では扱いにくい。そこで、エンタングル状態空間は、エンタングル演算子空間からの写像になっている。また、これらの空間間の写像は、1対1対応であるので、状態を演算子で置き換えて表現することとする。例えば、\([(\psi_1,|...0(0)10...>),(\psi_2,|...0(0)010...>)]\)は\([(\psi_1,\hat{a}_1^\dagger),(\psi_2,\hat{a}_2^\dagger)]\)となる。Haskellではこの表現を用いることにしよう。そこで、エンタングル演算子空間を新たなデータ型で表現することを考える。

エンタングル演算子空間はリストになっているので、リストの形態をとる新たなデータ型を代数的に定義（代数的データ型Entangle）しよう。要素をつなぐものを:&:とする。また、空のリストをEnZeroとして、次のように定義する。また優先度は5とする。

infixr 5 :&:

data Entangle a b 
  where
    EnZero  :: Entangle a b
    (:&:) :: (a, b) -> Entangle a b -> Entangle a b

このデータ型を表示するために、Showを定義しておこう。

instance (Show a, Read a, Eq a, Show b, Read b, Eq b, Ord b) => Show (Entangle a b)  where
    showsPrec _ EnZero   = showString ""
    showsPrec n ((xa, xb) :&: EnZero)   = showsPrec n xa . showString "_a" . showsPrec n xb . showString "^"
    showsPrec n ((xa, xb) :&: y)   = showsPrec n xa . showString "_a" . showsPrec n xb . showString "^ + " . showsPrec n y

上のプログラムで、空のリストの時はなにも出力しない。リストの要素が一つのときは、それを表す生成演算子を出力する。リストの要素が複数の時は、最初の要素を生成演算子で表し、その後に+をつけて出力する。

少し、プログラムを動かしてみよう。下のプログラムで、aからdまでは、Zeroから始めて、一つづつ状態を重ね合わせて作成したものである。eは、いくつかの状態を一緒に重ね合わせた例である。

*Ket> let a = EnZero
*Ket> a

*Ket> let b = (5.3, 1) :&: a
*Ket> b
5.3_a1^
*Ket> let c = (3.3, 3) :&: b
*Ket> c
3.3_a3^ + 5.3_a1^
*Ket> let d = (1.3, 2) :&: c
*Ket> d
1.3_a2^ + 3.3_a3^ + 5.3_a1^
*Ket> let e = (2.3, 1) :&: (4.2, -1) :&: (2.1, 2) :&: (3.2, 0) :&: EnZero
*Ket> e
2.3_a1^ + 4.2_a-1^ + 2.1_a2^ + 3.2_a0^

一緒に、Eqも定義しよう。但し、これを利用するときは、注意が必要である。1粒子の状態の重ね合わせは、生成演算子のリストになっているが、状態の重ね合わせを表している二つのリストに含まれている要素（生成演算子）が同じであっても、その順番が異なっているときはEqとはならないので、これを利用するときは、リストを昇順に並べてから比較することが要求される。

instance (Eq a, Ord a, Eq b, Ord b) => Eq (Entangle a b)  where
    Zero == Zero                     = True
    Zero == _                        = False
    _ == Zero                        = False
    (aa, ab) :&: b == (ca, cb) :&: d = (aa == ca) && (ab == cb) && (b == d)

これを利用してみよう。以下の例で、eとgは並び順まで同じ、状態の重ね合わせである。これに対して、hは並び順は異なるが、先の二つと同じ1粒子の状態の重ね合わせである。実行すると、次のようになる。

*Ket> let e = (2.3, 1) :&: (4.2, -1) :&: (2.1, 2) :&: (3.2, 0) :&: Zero
*Ket> let g = (2.3, 1) :&: (4.2, -1) :&: (2.1, 2) :&: (3.2, 0) :&: Zero
*Ket> let h = (2.1, 2) :&: (4.2, -1) :&: (2.3, 1) :&: (3.2, 0) :&: Zero
*Ket> e == g
True
*Ket> g == h
False

リストを昇順に並べることが必要になったので、その関数も定義しておく。おなじみのソートプログラムなので、簡単に理解してもらえると思うが、生成演算子が表す格子点の場所に基づいて、昇順に並べた。

esort :: (Eq b, Ord b) => Entangle a b -> Entangle a b
esort EnZero = EnZero
esort ((xa,xb) :&: xs) = esort (smaller xs) &&& ((xa,xb) :&: EnZero) &&& esort (larger xs)
    where 
      smaller xs = smaller' xs EnZero
      smaller' EnZero s    = s 
      smaller' ((ya, yb) :&: ys) s = if yb < xb then smaller' ys ((ya, yb) :&: s) else smaller' ys s 
      larger xs  = larger' xs EnZero
      larger'  EnZero s    = s
      larger'  ((ya, yb) :&: ys) s = if yb >= xb then larger' ys ((ya, yb) :&: s) else larger' ys s
infixr 5 &&&
(&&&) :: Entangle a b -> Entangle a b -> Entangle a b
(&&&) a b = connect a b
    where 
      connect EnZero b = b
      connect (x :&: xs) b = x :&: connect xs b

なお、上記のプログラムで、関数(&&&)は二つのリストを結合する。

これを用いて確かめてみよう。

*Ket> let g = (2.3, 1) :&: (4.2, -1) :&: (2.1, 2) :&: (3.2, 0) :&: EnZero
*Ket> let h = (2.1, 2) :&: (4.2, -1) :&: (2.3, 1) :&: (3.2, 0) :&: EnZero
*Ket> esort g
4.2_a-1^ + 3.2_a0^ + 2.3_a1^ + 2.1_a2^
*Ket> esort h
4.2_a-1^ + 3.2_a0^ + 2.3_a1^ + 2.1_a2^
*Ket> esort g == esort h
True

それでは、1粒子の状態の重ね合わせが二つあった時、その加算を定義しよう。加算は(+&)で定義する。状態の重ね合わせをxとyにする。加算は、格子点の場所が同じもの同士で、その係数を加えればよい。そこで、xとyをそれぞれ昇順に並べておいて、それぞれの先頭から、係数と格子点の番号を取り出しては、見比べながら、加算を実行するという処理を繰り返すが、それは次のようになる。
0)加算を行うと、二つの状態の重ね合わせを表す新たのリストを出力するが、これを加算後のリストとし、最初は空のリストとする。
1)格子点の番号が異なるときは、それが小さい方を処理済みとし、出来上がりつつある加算後のリストに付け加える。そして、また、同様のことを繰り返す。2)同じときは、二つを処理済みとし、両方の係数を足し合わせ、それに格子点の番号をつけて、出来上がりつつある加算後のリストに付け加える。そして、同様のことを繰り返す。
2)片方のリストが空になった時は、他方のリストをこれまでに得られている加算後のリストに付け加える。最後に、昇順となっていないので、加算後のリストをソートして出力する。

プログラムは次のようになる。

infixr 5 +&
(+&) :: (Num a, Eq b, Ord b) => Entangle a b -> Entangle a b -> Entangle a b
(+&) x y = esort $ (+&&) (esort x) (esort y) EnZero
    where
      infixr 5 +&&
      (+&&) :: (Num a, Eq b, Ord b) => Entangle a b -> Entangle a b -> Entangle a b -> Entangle a b
      (+&&) x EnZero s = x &&& s
      (+&&) EnZero y s = y &&& s
      (+&&) ((xa,xb) :&: xs) ((ya,yb) :&: ys) s
        | xb < yb = (+&&) xs ((ya,yb) :&: ys) ((xa,xb) :&: s)
        | xb > yb = (+&&) ((xa,xb) :&: xs) ys ((ya,yb) :&: s)
        | otherwise = (+&&) xs ys ((xa + ya,xb) :&: s)

実行例を示す。

*Ket> let a = EnZero
*Ket> let b = (5.3, 1) :&: a
*Ket> let c = (3.3, 3) :&: b
*Ket> let d = (1.3, 2) :&: c
*Ket> d
1.3_a2^ + 3.3_a3^ + 5.3_a1^
*Ket> let e = (2.3, 1) :&: (4.2, -1) :&: (2.1, 2) :&: (3.2, 0) :&: EnZero
*Ket> e
2.3_a1^ + 4.2_a-1^ + 2.1_a2^ + 3.2_a0^
*Ket> let f = d +& e
*Ket> f
4.2_a-1^ + 3.2_a0^ + 7.6_a1^ + 3.4000000000000004_a2^ + 3.3_a3^

それでは、エンタングル演算子空間での表現をエンタングル状態空間で表すことにしよう。この関数はprEntangleとする。前々回の記事で定義したKetを分かりやすく表示するプログラムprKetを利用すると、とても簡単にプログラミングできる。何とも、簡単だったので、どのようになっているかは、読者の方で解読して欲しい。

prEntangle :: (Show a, Num a, Show b, Num b, Eq b, Ord b) => Entangle a b -> String
prEntangle EnZero = ""
prEntangle ((xa, xb) :&: EnZero) = "(" ++ show xa ++ ")" ++ prKet (liftKet xb)
prEntangle ((xa, xb) :&: y) = "(" ++ show xa ++ ")" ++ prKet (liftKet xb) ++ " + " ++ prEntangle y

liftKet :: a -> Ket a
liftKet a = a :+: KetZero

実行例を示す。

*Ket> let a = EnZero
*Ket> prEntangle a
""
*Ket> let b = (5.3, 1) :&: a
*Ket> prEntangle b
"(5.3)|...0000(0)1000...>"
*Ket> let c = (3.3, 3) :&: b
*Ket> prEntangle c
"(3.3)|...000000(0)001000...> + (5.3)|...0000(0)1000...>"
*Ket> let d = (1.3, 2) :&: c
*Ket> prEntangle d
"(1.3)|...00000(0)01000...> + (3.3)|...000000(0)001000...> + (5.3)|...0000(0)1000...>"
*Ket> d
1.3_a2^ + 3.3_a3^ + 5.3_a1^
*Ket> let e = (2.3, 1) :&: (4.2, -1) :&: (2.1, 2) :&: (3.2, 0) :&: EnZero
*Ket> prEntangle e
"(2.3)|...0000(0)1000...> + (4.2)|...0001(0)000...> + (2.1)|...00000(0)01000...> + (3.2)|...0001000...>"
*Ket> let f = d +& e
*Ket> prEntangle f
"(4.2)|...0001(0)000...> + (3.2)|...0001000...> + (7.6)|...0000(0)1000...> + (3.4000000000000004)|...00000(0)01000...> + (3.3)|...000000(0)001000...>"

さて、最後は正規化だ。それぞれの係数を二乗し、その平方根で、それぞれの係数を割れば求めるものが得られる。プログラムは次のようになる。

normalize  :: (Floating a) => Entangle a b -> Entangle a b
normalize EnZero = EnZero
normalize x = normalize' x
    where
      total = sqrt $ sum x 0
      sum :: (Floating a) => Entangle a b -> a -> a
      sum EnZero s = s
      sum ((xa, xb) :&: y) s = sum y (xa * xa + s)
      normalize' EnZero = EnZero

実行例を見ることにしよう。

*Ket> let a = EnZero
*Ket> normalize a

*Ket> prEntangle $ normalize a
""
*Ket> let b = (5.3, 1) :&: a
*Ket> normalize b
1.0_a1^
*Ket> prEntangle $ normalize b
"(1.0)|...0000(0)1000...>"
*Ket> let c = (3.3, 3) :&: b
*Ket> normalize c
0.5285584527450004_a3^ + 0.8488969089540915_a1^
*Ket> prEntangle $ normalize c
"(0.5285584527450004)|...000000(0)001000...> + (0.8488969089540915)|...0000(0)1000...>"
*Ket> let d = (1.3, 2) :&: c
*Ket> normalize d
0.20384791140942493_a2^ + 0.5174600828085402_a3^ + 0.8310722542076554_a1^
*Ket> prEntangle $ normalize d
"(0.20384791140942493)|...00000(0)01000...> + (0.5174600828085402)|...000000(0)001000...> + (0.8310722542076554)|...0000(0)1000...>"
*Ket> let e = (2.3, 1) :&: (4.2, -1) :&: (2.1, 2) :&: (3.2, 0) :&: EnZero
*Ket> normalize e
0.37518843943785457_a1^ + 0.6851267154952128_a-1^ + 0.3425633577476064_a2^ + 0.5220013070439716_a0^
*Ket> prEntangle $ normalize e
"(0.37518843943785457)|...0000(0)1000...> + (0.6851267154952128)|...0001(0)000...> + (0.3425633577476064)|...00000(0)01000...> + (0.5220013070439716)|...0001000...>"
*Ket> let f = d +& e
*Ket> normalize f
0.40397689977733287_a-1^ + 0.3077919236398727_a0^ + 0.7310058186446975_a1^ + 0.32702891886736474_a2^ + 0.3174104212536187_a3^
*Ket> prEntangle $ normalize f
"(0.40397689977733287)|...0001(0)000...> + (0.3077919236398727)|...0001000...> + (0.7310058186446975)|...0000(0)1000...> + (0.32702891886736474)|...00000(0)01000...> + (0.3174104212536187)|...000000(0)001000...>

８．５　プログラム全体

前々回のプログラムと合わせて全体を示すと次のようになる。

{-#LANGUAGE GADTs #-}

module Ket (Ket (Zero, KetZero, (:+:)), (+^), (-^), prKet) where

infixr 5 :+:
data Ket a where
  Zero :: Ket a  -- Don't use it when defining a Bra. It is only used when operating Ket data.
  KetZero :: Ket a
  (:+:) :: a -> Ket a -> Ket a

infixr 5 +^
(+^) :: (Eq a, Ord a) =>  a -> Ket a -> Ket a
(+^) _ Zero = Zero
(+^) a b = a :+: b

infixr 5 -^
(-^) :: (Eq a, Ord a) => a -> Ket a -> Ket a
(-^) _ Zero = Zero
(-^) a b
  | b == c = Zero
  | otherwise = c 
    where
      c = delete a b
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

instance (Eq a, Ord a) => Eq (Ket a)  where
    Zero == Zero = True
    Zero == _    = False
    _    == Zero = False
    KetZero == KetZero = True
    KetZero == _       = False
    _       == KetZero = False
    (a :+: b) == (c :+: d) = (a == c) && (b == d)

instance (Show a, Read a, Eq a, Ord a) => Show (Ket a)  where
    showsPrec _ Zero   = showString "0"
    showsPrec _ KetZero   = showString "| ...00(0)00... >"
    showsPrec n (a :+: b)   = showString ",a" . showsPrec n a . showString "+" . showsPrec n b

prKet :: (Eq a, Ord a, Num a, Show a) => Ket a -> String
prKet Zero = "0"
prKet KetZero = "|...000(0)000...>"
prKet a = "|..." ++ prKet' (ksort' $ ksort a) [] "right" 0 0 ++ "...>"
    where
      prKet' :: (Eq a, Ord a, Num a, Show a) => Ket a -> String -> String -> a -> a -> String
      prKet' KetZero s "left" _ num  = "000" ++ show num ++ s ++ "000" 
      prKet' KetZero s "right" _ num = "000" ++ s ++ show num ++ "000"
      prKet' (a :+: b) s dir index num
        | dir == "right" && index == a    = prKet' b s dir index (num + 1)
        | dir == "right" && index == 0    = prKet' (a :+: b) (s ++ "(" ++ show num ++ ")") "left" (index + 1) 0
        | dir == "right"                  = prKet' (a :+: b) (s ++ show num) "left" (index + 1) 0 
        | dir == "left"  && index == (-a) = prKet' b s dir index (num + 1)
        | otherwise                       = prKet' (a :+: b) (show num ++ s) "right" index 0 

ksort :: Ord a => Ket a -> Ket a
ksort KetZero = KetZero
ksort (x :+: xs) = ksort (smaller xs) +++ (x :+: KetZero) +++ ksort (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if y < x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if y >= x then larger' ys (y :+: s) else larger' ys s

ksort' :: (Num a, Ord a) => Ket a -> Ket a
ksort' KetZero = KetZero
ksort' (x :+: xs) = ksort' (smaller xs) +++ (x :+: KetZero) +++ ksort' (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if abs y < abs x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if abs y >= abs x then larger' ys (y :+: s) else larger' ys s

infixr 5 +++
(+++) :: Ket a -> Ket a -> Ket a
(+++) a b = connect a b
    where 
      connect KetZero b = b
      connect (x :+: xs) b = x :+: connect xs b 

reverse1 :: Ket a -> Ket a
reverse1 x = reverse' x KetZero
    where
      reverse' KetZero s = s
      reverse' (y :+: ys) s = reverse' ys (y :+: s)

infixr 5 :&:

data Entangle a b 
  where
    EnZero  :: Entangle a b
    (:&:) :: (a, b) -> Entangle a b -> Entangle a b

esort :: (Eq b, Ord b) => Entangle a b -> Entangle a b
esort EnZero = EnZero
esort ((xa,xb) :&: xs) = esort (smaller xs) &&& ((xa,xb) :&: EnZero) &&& esort (larger xs)
    where 
      smaller xs = smaller' xs EnZero
      smaller' EnZero s    = s 
      smaller' ((ya, yb) :&: ys) s = if yb < xb then smaller' ys ((ya, yb) :&: s) else smaller' ys s 
      larger xs  = larger' xs EnZero
      larger'  EnZero s    = s
      larger'  ((ya, yb) :&: ys) s = if yb >= xb then larger' ys ((ya, yb) :&: s) else larger' ys s
infixr 5 &&&
(&&&) :: Entangle a b -> Entangle a b -> Entangle a b
(&&&) a b = connect a b
    where 
      connect EnZero b = b
      connect (x :&: xs) b = x :&: connect xs b

infixr 5 +&
(+&) :: (Num a, Eq b, Ord b) => Entangle a b -> Entangle a b -> Entangle a b
(+&) x y = esort $ (+&&) (esort x) (esort y) EnZero
    where
      infixr 5 +&&
      (+&&) :: (Num a, Eq b, Ord b) => Entangle a b -> Entangle a b -> Entangle a b -> Entangle a b
      (+&&) x EnZero s = x &&& s
      (+&&) EnZero y s = y &&& s
      (+&&) ((xa,xb) :&: xs) ((ya,yb) :&: ys) s
        | xb < yb = (+&&) xs ((ya,yb) :&: ys) ((xa,xb) :&: s)
        | xb > yb = (+&&) ((xa,xb) :&: xs) ys ((ya,yb) :&: s)
        | otherwise = (+&&) xs ys ((xa + ya,xb) :&: s)

instance (Eq a, Eq b, Ord b) => Eq (Entangle a b)  where
    EnZero == EnZero                   = True
    EnZero == _                        = False
    _ == EnZero                        = False
    (aa, ab) :&: b == (ca, cb) :&: d = (aa == ca) && (ab == cb) && (b == d)


instance (Show a, Read a, Eq a, Show b, Read b, Eq b, Ord b) => Show (Entangle a b)  where
    showsPrec _ EnZero   = showString ""
    showsPrec n ((xa, xb) :&: EnZero)   = showsPrec n xa . showString "_a" . showsPrec n xb . showString "^"
    showsPrec n ((xa, xb) :&: y)   = showsPrec n xa . showString "_a" . showsPrec n xb . showString "^ + " . showsPrec n y

prEntangle :: (Show a, Num a, Show b, Num b, Eq b, Ord b) => Entangle a b -> String
prEntangle EnZero = ""
prEntangle ((xa, xb) :&: EnZero) = "(" ++ show xa ++ ")" ++ prKet (liftKet xb)
prEntangle ((xa, xb) :&: y) = "(" ++ show xa ++ ")" ++ prKet (liftKet xb) ++ " + " ++ prEntangle y

liftKet :: a -> Ket a
liftKet a = a :+: KetZero

normalize  :: (Floating a) => Entangle a b -> Entangle a b
normalize EnZero = EnZero
normalize x = normalize' x
    where
      total = sqrt $ sum x 0
      sum :: (Floating a) => Entangle a b -> a -> a
      sum EnZero s = s
      sum ((xa, xb) :&: y) s = sum y (xa * xa + s)
      normalize' EnZero = EnZero
      normalize' ((xa, xb) :&: y) = (xa / total, xb) :&: normalize' y

身近な存在としての量子力学（９）：重ね合わせ

８．重ね合わせ

量子力学の世界は不思議な世界だ。別荘の玄関に、お腹の羽毛が黄色い鶺鴒（セキレイ：写真はWikipediaのcommonsより）が巣を作り、子育てをしている。オスとメスに差がないので、どちらが卵を抱いているのかわからない。もし、卵を抱いている親がメスだとすると、外で餌を探しているのはオスである。この逆もありうる。

量子力学の世界では、一つのものが二つの状態をとることができる。上の例に倣って、鳥を考えることにしよう。ただし、量子力学の世界の鳥なので、量子の鳥と呼ぶことにする。そして、ここは量子力学の世界なので、いずれの鳥もオスになることもできるし、メスになることもできるとしよう。

次のような系を考える。量子の鳥がつがいでいるとしよう。即ち、一方がオスなら他方は必ずメスとする。さて、鳥がどちらの性であるかを観察することにしよう。どちらの鳥も、オスにもなるし、メスにもなる。しかし、観察したときは必ずどちらかの性である。今、一方の鳥を観察したときに、それがオスだとわかったとする。この時は、他方の鳥はメスということになる。これは観察せずに分かったことになる。何とも不思議な話なのだが、量子力学の世界ではこのようなことが生じる。これは、アインシュタインが最も受け入れがたいと思った事象である。

量子力学の世界では、扱っているのは、量子の鳥ではなく、とても小さな粒子である。粒子が複数の状態をとっていることを量子の重ね合わせという。今回は、この重ね合わせについて考えてみよう。

今回の記事では、線形結合などの概念が使われる。復習が必要な人は次の節を読んでほしい。そうでない人は、8.1節に進んでほしい。

８．０　線形結合

状態の重ね合わせをいきなり説明するのはハードルが大きすぎるので、たとえ話で下ごしらえすることにしよう。今、魚の鯛とお菓子のやい焼きを考えてみよう。鯛を\(s\)で、たこ焼きを\(t\)で表すことにする。鯛が\(m\)匹いる状態は\(ms\)で表すこととする。同様に、たこ焼きが\(n\)個ある状態は\(nt\)で表すこととする。\(m\)と\(n\)を直接加算することはできないが、この状況は数学的には、\(ms+nt\)と表すことができる。この時、\(ms+nt\)を\(s\)と\(t\)の線形結合という。

鯛が\(m\)匹とたこ焼きが\(n\)個あるところに、それぞれ、鯛を\(m'\)匹とたこ焼きを\(n'\)加えたとする。この時の状態は、\( (m+m')s+(n+n')t\)で表すことができる。もっともなことだが、同じ種類のものに対しては足すことができる（数学的には、\(s\)と\(t\)が張る線形空間では、それぞれの係数に対しては四則演算を作用させることができる）。

さて、今、考えている世界は、現実の世界ではなく、量子の世界だとしよう。一つの物質が鯛とたい焼きの二つの状態をとれるものとする。その物質を観察したとする。何回か観察した結果、鯛と見えたのが\(A\)回、たい焼きと見えたのが、\(B\)回であったとする。この時の状態を現実世界での鯛とたい焼きの関係をまねるが、係数は平方根にして、\(\sqrt {A}s+\sqrt {B}t\)と表すことにしよう。この場合も、これは\(s\)と\(t\)の線形結合になっている。

この物資を前とは違う別の方法で観察したとしよう。その時、鯛を\(A'\)回、たい焼きを\(B'\)回観察したとする（ただし、観察した回数は同じだとする。即ち、\(A+B=A'+B'\)）。この時の状態は、\(\sqrt {A'}s+\sqrt {B'}t\)で表すことができる。

この時、二つの方法を重ね合わせた状態は、\((\sqrt{A}+\sqrt{A'})s+(\sqrt{B}+\sqrt{B'})t\)となる。

下ごしらえが済んだので、まず、前回の記事で説明した粒子の状態と生成演算子・消滅演算子の関係を整理しておこう。

８．１　演算子と状態の空間

\(\hat{a}_i^\dagger|KetZero>\)は、真空の状態から、\(i\)番目の格子点に1粒子が存在する状態を作り出した。演算子\(\hat{a}_i^\dagger\)や演算子\(\hat{a}_i\)、あるいは、これらを結合したものは、状態に対する演算を与える。今、演算子あるいは演算子を結合したものの集まりを集合と考えることにする。また、状態も集合と考えると、演算子で作られる集合(演算子空間:\(B^A\)と呼ぶ)から状態の集合(これを状態空間:\(A\)と呼ぶ)への写像を考えることができる。演算子空間は真空の状態\(|KetZero>\)を状態空間に写像する(真空の状態だけで作られる空間を真空空間:\(B\)と呼ぶ)。図で示すと以下のようになる。図からわかるように、何も演算を行わないときは0とし、これも、演算子空間に加えた。0を作用させると、状態空間には移らずに、状態ではないところ、即ち、0に移る。これは、粒子のないところに消滅演算子を施したときに、状態とはらない、即ち、0となるといったが、それと同じ働きをする。
これより、演算子空間から状態空間への写像は部分写像であることが分かる。これに対して、状態空間から演算子空間への写像は、１対多の写像であることが分かる。

８．２　重ね合わせでの演算子と状態の空間

さて、状態の重ね合わせを考えることにしよう。これまでも説明してきたが、状態とは、どの格子点に何個粒子が存在しているかを示すものであった。例えば、2番目の格子点に粒子が1個存在する場合には\(|...000\dot{0}01000...>\)と1番目の格子点に粒子が1個と-2番目の格子点に粒子が2個存在する存在する場合には\(|...00020\dot{0}1000...>\)と表すことができた。

それでは、前者と後者が同時に存在する場合、即ち、量子力学でいう重ね合わせが生じた場合はどうしたらよいであろうか。二つの状態が同時に生じているので、集合論的に考えると、論理和でよさそうである（一つの状態を\(A\)もう一つの状態を\(B\)とした時、これらの論理は、即ち、いずれかの状態を取っているときは\(A\cup B\)である）。そこで、量子力学での通例に倣って、\(\cup\)ではなく、\(+\)で重ね合わせを表すこととすると、先ほどの二つの状態の重ね合わせは、\(|...000\dot{0}01000...>+\ |...00020\dot{0}1000...>\)となる。

重ね合わせの状態は外部から観察すると、一つの状態だけが観測される。そこで、観察される頻度を重ね合わせに反映させることにしたい。例えば、先の二つの重ね合わせで、\(\psi_1|...000\dot{0}01000...>+\ \psi_2|...00020\dot{0}1000...>\)のような形態で表現することとし\(\psi_1,\psi_2\)が観察される頻度を何らかの形で反映されるようにしたい。ここでは、まだ説明をしないが、一方を観察した回数を\(A\)、他方を観察した回数を\(B\)とする。この時、\(\psi_1=\sqrt{A},\psi_2=\sqrt{B}\)ということにする。\(A,B\)が回数ではなく頻度（確率）を表している場合には、\(\psi_1^2+\psi_2^2=1\)となる。この時、\(\psi_1,\psi_2\)は正規化されているという。

だいぶ議論が整理されてきたので、もう少し、概念的な話を前に進めよう。ここまでは、話を一般的にするために、一つの状態の中にいくつもの粒子が存在するとして論じてきた。しかし、ここからは、話を少し簡単にするために、どの状態も1粒子の存在だけを表しているものとする。即ち、\(|...000\dot{0}01000...>\)のようなものは許すが、\(|...00020\dot{0}1000...>\)のようなものは当面対象としないこととする。即ち、我々が考えるものは、
\(...\psi_{-2}|...00010\dot{0}000...>+\psi_{-1}|...0001\dot{0}000...>+\psi_{0}|...000\dot{1}000...>\)
\(+\psi_{1}|...000\dot{0}1000...>+\psi_{2}|...000\dot{0}01000...>...\)
である。

この式は、
\(\sum_{i=-\infty}^\infty{(\psi_i\hat{a}_{i}^\dagger|KetZero>)}\)
\(=...\psi_{-2}\hat{a}_{-2}^\dagger|KetZero>+\psi_{-1}\hat{a}_{-1}^\dagger|KetZero>+\psi_{0}\hat{a}_{0}^\dagger|KetZero>\)
\(+\psi_{1}\hat{a}_{1}^\dagger|KetZero>+\psi_{2}\hat{a}_{2}^\dagger|KetZero>...\)
と変形できるので、
\(..., \hat{a}_{-2}^\dagger|KetZero>\),\( \hat{a}_{-1}^\dagger|KetZero>\),\( \hat{a}_{0}^\dagger|KetZero>\),\( \hat{a}_{1}^\dagger|KetZero>\),\( \hat{a}_{2}^\dagger|KetZero>,...\)
の、即ち、\(\hat{a}_{i}^\dagger|KetZero>\)の線形結合である。

さらに進めて、\(\sum_{i=-\infty}^\infty{(\psi_i\hat{a}_{i}^\dagger|KetZero>)}=(\sum_{i=-\infty}^\infty{\psi_i\hat{a}_{i}^\dagger})|KetZero>\)と変形することもできる。そこで、下図に示すような演算子の空間を考えると、先の式は演算子の空間だけで表すことが可能である。これは次のようになる。
\(\Psi=\sum_{i=-\infty}^\infty{\psi_i\hat{a}_{i}^\dagger}\)
この式は、\(\hat{a}_{i}^\dagger\)の線形結合である。

ここまで来ると、重ね合わせに対する考え方は随分とすっきりしてくる。

ところで、1粒子の観察は、一か所、あるいは、一つの方法で行っているとは限らない。複数の個所で、あるいは、複数の方法で行っているかもしれない。
例えば、光の干渉性を示す実験に、有名なヤングの実験があるが、それは二重のスリットを設けて、一方のスリットから出てくる光と、他方のスリットから出てくる光とを重ね合わせて実験を行っていた。図に、WikiPediaに掲載されているものを利用するとヤングの実験は次のようになっている。

そこで別の方法で観察して得られた粒子の位置が次のようであったとしよう。
\(\hat{\Phi}^\dagger=\sum_{i=-\infty}^\infty{\phi_i \hat{a}_i^\dagger}\)

この時、状態は線形結合となると仮定しているので、\(\hat{a}_i\)の各係数を加えることができる。
\(\hat{\Psi}^\dagger+\hat{\Phi}^\dagger=\sum_{i=-\infty}^\infty{(\psi_i+\phi_i) \hat{a}_i^\dagger}\)

これらが作る状態は、次のようになる。
\((\hat{\Psi}^\dagger+\hat{\Phi}^\dagger)|KetZero>=\sum_{i=-\infty}^\infty{(\psi_i+\phi_i) \hat{a}_i^\dagger|KetZero>}\)

さて、重ね合わせの度合いを示す係数\(\psi_i\)を説明しよう。
\(\psi_i\)は一般には複素数である。格子点の\(i\)番目で、粒子が見つかる確率\(P_i\)は、\(\psi_i\)の共役複素数を\(\psi_i^*\)とした時(共役複素数とは、虚数部の符号を反対にしたものである。\(a+ib\)の共役複素数は\(a-ib\)である）、
\(P_i=\frac{\psi_i \psi_i^*}{ \sum_{i=-\infty}^\infty{\psi_i \psi_i^*}}\)
である。

\(\sum_{i=-\infty}^\infty{\psi_i \psi_i^*}=1\)のとき、
\(\psi_i\)は正規化されているという。その時、粒子が格子点の\(i\)番目で観察される確率は、\(P_i=\psi_i \psi_i^*\)である。

例を挙げることにしよう。1粒子の重ね合わせが一つの方法では次のようになっていたとする。
\(\hat{\Psi}^\dagger=\frac{1}{\sqrt{2}}\hat{a}_0^\dagger+\frac{1}{\sqrt{2}}\hat{a}_1^\dagger\)
この時、格子点が0番目と1番目では粒子が存在する確率は1/2である。即ち、\(\psi_0=\psi_0^*=\frac{1}{\sqrt{2}},\psi_1=\psi_1^*=\frac{1}{\sqrt{2}}\) である。

また、粒子の重ね合わせを別の方法では次のように得たとする。
\(\hat{\Phi}^\dagger=\frac{1}{\sqrt{2}}\hat{a}_0^\dagger-\frac{1}{\sqrt{2}}\hat{a}_1^\dagger\)
この時、格子点が0番目と1番目では粒子が存在する確率は前と同様に1/2である。即ち、\(\phi_0=\phi_0^*=\frac{1}{\sqrt{2}},\phi_1=\phi_1^*=\frac{1}{\sqrt{2}}\)である。

それでは、この二つの方法を重ね合わせたらどのようになるであろうか。
\(\hat{\Psi}^\dagger+\hat{\Phi}^\dagger=\sqrt{2}\hat{a}_0^\dagger\)
となる。確率の合計が1になるように正規化すると
\(\hat{\Psi}^\dagger+\hat{\Phi}^\dagger=\hat{a}_0^\dagger\)
である。即ち、この2粒子を重ね合わせると、1番目では干渉を起こして粒子が存在しないことになる。粒子が観測されるのは、常に0番目の格子点ということになり、不思議な現象が生じる。

８．３　Haskellで表現できるようにする

今までの話をHaskellで表現できるようにしよう。少し、間を取ることにして、次の図を参考に考えて欲しい。

身近な存在としての量子力学（８）：ケットをHaskellで表現する

７．ケットをHaskellで表現する

ケットをHaskellで実現することにしよう。プログラムは実装すること自体には、それほど時間を取られることはない。せいぜい数十分、長くても数時間だ。しかし、設計には多くの時間をいつも費やしている。世の中には、これとは逆の人もいるらしいが、手直しが続き、結局は、無駄な多くの時間を浪費しているのではないかと思う。

設計しているときは、それだけを一途にというわけではない。この作業をしている時の姿は、はた目から見ると無駄なことをしているなと感じられることと思う。今回も、ケットの基本的な概念を頭の隅に残して、友人から頂いた、藤沢周平の『三屋清左衛門残日録』と高田郁『八朔の雪』を読むことに集中した。

三屋清左衛門残日録は、隠居したばかりの武士の気持ちの移り変わりと、その後に展開する藩での事件を解決に導く手腕を描いた小説である。話の筋もなかなか面白いのだが、今回は、なぜか、文章の書き方に目を奪われることが多かった。一つ一つの文が、また、一つ一つの単語が、とてもきれいに配置されていて、素晴らしい書き手だなあと恐れ入った。今設計しようとたくらんでいるプログラムもこのようにきれいに書けると素晴らしいのだがと対比づけて読んだ。

八朔の雪は、澪と呼ばれる若い女性が江戸で評判となる料理を開発していく様子を描いた小説である。数々の艱難辛苦が待ち受けているのだが、それを一つ一つ乗り越えていく姿に涙を誘われる。経営学のイノベーションの視点からとらえても面白そうなのだが、料理の開発と日常での出来事がうまく織りなされていて、構成が面白いなと思って読んだ。最終講義に寄せて、数学の話と日常生活の話を織り交ぜたエッセイを書いてみた。分かりやすく書いたつもりではあったが、数学のところは読み飛ばした人が多いようであった。専門的なことと日常的なことを織り交ぜることの難しさを知っていたので、この本は私にとってこれから文章を書くときに、随分と役立つことだろうと思っている。

この二つの本を読み終わったころには、頭の中で設計が完了していたので、それを元にプログラムの形にした。

７．１　ケットの表し方

前の記事で紹介したように、格子点を使っての粒子の表し方は下図のようにしていた。
\( | ...00 \dot{0} 00200...>\)

この表現、目には優しいのだが、プログラム内部での表現としては難しいことがいくつもある。格子点の0番目には数字の上にドットがついているが、これをどのように表したらよいのかは悩ましい問題である。また、格子点は正と負に対して無限の数を取るので、これをどのように表すかも、同じように、いやらしい問題である。

表し方はいろいろあるだろうが、全てが0であるケットを次のように用意する。
\( |KetZero>\)

また、粒子が0でない格子点にはケットの中に粒子の数を書くのではなく、生成演算子\(\hat{a}^\dagger\)を用いて表すことにする。
例えば、格子点が１番目のところに粒子が1個の時は、
\(\hat{a}^\dagger_1 |KetZero>\)
と表す。格子点が１番目のところに粒子が2個の時は
\(\hat{a}^\dagger_1 \hat{a}^\dagger_1|KetZero>\)
とする。格子点が１番目と-2番目のところにそれぞれ粒子が1個の時は
\(\hat{a}^\dagger_{-2} \hat{a}^\dagger_1 |KetZero>\)
とする。

７．２　Haskellでケットを実現

ケットを
\(\hat{a}^\dagger_{-2} \hat{a}^\dagger_1 |KetZero>\)
で表すことにしたので、これを、Haskellのデータ型として用意する必要がある。

どうしたらよいだろうか。

ここまでの話で、答えが分かった人はスマートは人だと思う。リストに何となく似ていると思わないだろうか。代表的な例は文字列だ。
例えば、"word"という単語は、Haskellでは、

'w' : 'o' :'r' :'d' : []

と表すことができる。右端に空のリスト[ ]があり、その左側に、そこに入っていく文字が、その順番に従って並べられている。

リストとケットが同じ構造であることは、空のリスト[ ]をKetZeroで、文字を生成演算子で置き換えることで納得できるだろう。

リストは、代数的データ型を用いて次のように定義されている。

infixr 5 :
data [] a = [] | a : [a]

そこで、ケットはこれに倣って次のように定義しよう。

infixr 5 :+:
data Ket a  = KetZero | a :+: Ket a deriving (Show, Read, Eq, Ord)

リストは:で要素を結合させているが、ケットは新たな演算子を設けて:+:で結合させることにしよう。そして、リストと同じように右側から結合するので、infixrで定義し、その優先度は5としよう。
この定義をファイルKet.hsに格納する。そして、これを読みだし、利用する例をいくつか示そう。

Prelude> :load "Ket.hs"
[1 of 1] Compiling Ket              ( Ket.hs, interpreted )
Ok, modules loaded: Ket.
*Ket> let a = KetZero
*Ket> a
KetZero
*Ket> let b = 1 :+: KetZero
*Ket> b
1 :+: KetZero
*Ket> let c = 2 :+: (-1) :+: b
*Ket> c
2 :+: (-1 :+: (1 :+: KetZero))

上記の例で、aはKetZeroとした。また、bは格子点が1番目のところに粒子が一つある場合である。cはbに付け加えて、2と-1番目にさらに粒子が一つある場合である。

格子点の番号の小さい方から生成演算子を順番に並べる関数ksortを用意しよう。これは次のようになる。

ksort :: Ord a => Ket a -> Ket a
ksort KetZero = KetZero
ksort (x :+: xs) = ksort (smaller xs) +++ (x :+: KetZero) +++ ksort (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = s 
      smaller' (y :+: ys) s = if y < x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = s
      larger'  (y :+: ys) s = if y >= x then larger' ys (y :+: s) else larger' ys s

infixr 5 +++
(+++) :: Ket a -> Ket a -> Ket a
(+++) a b = connect a b
    where 
      connect KetZero b = b
      connect (x :+: xs) b = x :+: connect xs b 

ksortのプログラムは、Haskell入門で紹介した記事のquicksortと考え方は同じである。その時は次のようになっていた。

quicksort [] = []
quicksort (x:xs) = quicksort smaller ++ [x] ++ quicksort larger
  where
    smaller = [a | a <- xs, a <  x]
    larger = [a | a <- xs, a >= x]

quicksortでは、リストとリストを接続するのに、関数++を用いていたが、Ketでは、それらを接続するときは関数+++を用いるものとし、上記のように定義する。

それでは、これを用いてみよう。

Prelude> :load "Ket.hs"
[1 of 1] Compiling Ket              ( Ket.hs, interpreted )
Ok, modules loaded: Ket.
*Ket> let a = 5 :+: 1 :+: 2 :+: (-1) :+: 3 :+: KetZero
*Ket> a
5 :+: (1 :+: (2 :+: (-1 :+: (3 :+: KetZero))))
*Ket> ksort a
-1 :+: (1 :+: (2 :+: (3 :+: (5 :+: KetZero))))
*Ket> 

７．３　Haskellで生成・消滅演算子を実現

生成演算子\(\hat{a}^\dagger\)と消滅演算子\(\hat{a}\)をHaskellでは関数+^と関数-^で表すことにしよう。関数+^は、ケットのデータ型での定義a :+: Ket aと同じなので、次のようにする。

infixr 5 +^
(+^) :: a -> Ket a -> Ket a
(+^) a b = a :+: b

消滅演算子は少し厄介である。粒子がないところから粒子を取り去ろうとするとケットではなくなり0になると前の記事では説明した。そこで、ここでは、このようなものは例外処理として表すこととする。即ち、このような場合には、エラー出力を出すこととし、次のようにする。

infixr 5 +^
infixr 5 -^
(-^) :: (Eq a, Ord a) => a -> Ket a -> Ket a
(-^) a b 
  | b == c = error "Nothing (0)"
  | otherwise = c 
    where
      c = delete a b
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

これらを含んだものをファイルKet.hsとし、これを読み込んで実行してみよう。

Prelude> :load "Ket.hs"
[1 of 1] Compiling Ket              ( Ket.hs, interpreted )
Ok, modules loaded: Ket.
*Ket> let a = KetZero
*Ket> a
KetZero
*Ket> let b = (+^) 1 a
*Ket> b
1 :+: KetZero
*Ket> let c =  (+^) (-1) b
*Ket> c
-1 :+: (1 :+: KetZero)
*Ket> let d =  (+^) 1 c
*Ket> d
1 :+: (-1 :+: (1 :+: KetZero))
*Ket> let e =  (-^) 1 d
*Ket> e
-1 :+: (1 :+: KetZero)
*Ket> let f =  (-^) 1 e
*Ket> f
-1 :+: KetZero
*Ket> let g =  (-^) 1 f
*Ket> g
*** Exception: Nothing (0)

前半は生成演算子を利用して粒子を増やしている。後半は消滅演算子を利用して粒子を減らしている。最後の例は、粒子の数が0のところから減らそうとしているのでエラーとなっている。

エラーが出るのが嫌であれば、Maybeを用いて、次のように定義することも可能である。

infixr 5 +^
infixr 5 -^
infixr 5 -^
(-^) :: (Eq a, Ord a) => a -> Ket a -> Maybe (Ket a)
(-^) a b 
  | b == c = Nothing
  | otherwise = Just c 
    where
      c = delete a b
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

７．４　ケットの内部表現を実現

これまでに表示されたケットは、一番最初に約束した表現
\(\hat{a}^\dagger_{-2} \hat{a}^\dagger_1 |KetZero>\)
とは異なる。

そこで、この表現で表示されるようにするために、Ketのデータを表示するためのshowを手動で定義することとする。少し曲がり道をしてみよう。一般的代数的データ型になれるために、代数的データ型で定義されていたKetを一般的代数的データ型を使って定義してみよう（ここは趣味の問題なので、もちろん前のままでもよい。ただしderiving以降は省くこと。私は、一般的代数的データ型の方が代数の構造を直截に表すので、こちらの方が好きである）。

infixr 5 :+:
data Ket a where
  KetZero :: Ket a
  (:+:) :: a -> Ket a -> Ket a

このときプログラムの先頭に次を加えることを忘れないようにしよう。

{-#LANGUAGE GADTs #-}

前に定義したものと同じだが、derivingがないことに注視して欲しい。そこで、クラスの継承関係を自分で定義しなければならない。手始めに、EqをKetで使えるようにする。これは次のようにする。

instance (Eq a, Ord a) => Eq (Ket a)  where
    KetZero == KetZero = True
    KetZero == _ = False
    _ == KetZero = False
    (a :+: b) == (c :+: d) = (a == c) && (b == d)

これは、Ket aをEqのインスタンスにするための定義である。最初の(Eq a, Ord a)はaはEqとOrdを利用できるデータ型と定義している。
等しいことの判定は、KetZeroに対するものと、a :+: bに対するもので分かれる。KetZeroの場合には、相手がKetZeroの場合だけ等しい。それ以外は等しくない。a :+: bの場合には、相手方もこのような形c :+: dになっていて、aとcそしてbとdが両方とも等しいとき等しくなり、それ以外は等しくない。

次のshowであるがこれは次のように実現した。

instance (Show a, Read a, Eq a, Ord a) => Show (Ket a)  where
    showsPrec _ KetZero   = showString "| ...00(0)00... >"
    showsPrec n (a :+: b)   = showString "a" . showsPrec n a . showString "^" . showsPrec n b

KetZeroの時は、ゼロが続くものを用意した。また、0番目の格子の位置は()でくくることとした。a :+: bの時は、aの部分は生成演算子で表すようにし、bについては同じことを繰り返すようにした。

プログラムを実行してみよう。

instance (Show a, Read a, Eq a, Ord a) => Show (Ket a)  where
Prelude> :load "Ket.hs"
[1 of 1] Compiling Ket              ( Ket.hs, interpreted )
Ok, modules loaded: Ket.
*Ket> let a = KetZero
*Ket> a
| ...00(0)00... >
*Ket> let b = 1 :+: a
*Ket> b
a1^| ...00(0)00... >
*Ket> let c = (+^) 3 b
*Ket> c
a3^a1^| ...00(0)00... >
*Ket> let d = (-1) :+: c
*Ket> d
a-1^a3^a1^| ...00(0)00... >
*Ket> ksort d
a-1^a1^a3^| ...00(0)00... >

設計時に、頭に描いたようにプログラムが機能していることが分かる。

７．５　プリティープリント

ここまでくると欲が出てくる。ケットを場の理論で説明していた形で表示したい。そこで、いわゆるプリティプリントを用意することにしよう。関数名は、prKetとしよう。

プログラムの大まかな考え方は次のようである。
1)生成演算子を格子点の大小順ではなく、0番目の位置からどれだけ離れているかで並べる。但し、同じ距離である場合には、負の方を先に並べるようにする。
2)並べ替えられた生成演算子を順番に辿り、真ん中から外へと粒子の数が並ぶようにする。
3)生成関数の処理がすべて終わったら、両端にケットの記号を付けて終了する。

これをもう少し正確に表現すると次のようになる。
1)生成演算子の順を小さいものからではなく、最初は0、次は-1、その次は1、さらに次は-2、その次は2、というように、0から始めて、その右そしてその左、さらにその右そしてその左という順番で並べる。そして、0番目での粒子の個数を書き（ただしこの場合に限りカッコをつける。
2)これを用いてその次は、左端に-1番目での粒子の数を書き次に右端に1番目での粒子の数を書き、さらにその次に、左端に-2番目での粒子の数を書き次に右端に2番目での粒子の数を書くということを続ける。
3)すべての生成演算子を処理したら、左右の端にそれぞれ000を三つ並べて、後はピリオドを繰り返しつけ、左右にケットのマークを付けて終了する。プログラムの動きの概略はこうだが、実際の動きは次のプログラムを参考にして欲しい。

prKet :: (Eq a, Ord a, Num a, Show a) => Ket a -> String
prKet KetZero = "|...000(0)000...>"
prKet a = "|..." ++ prKet' (ksort' $ ksort a) [] "right" 0 0 ++ "...>"
    where
      prKet' :: (Eq a, Ord a, Num a, Show a) => Ket a -> String -> String -> a -> a -> String
      prKet' KetZero _ _ 0 num  = "000" ++ "(" ++ show num ++ ")" ++ "000" 
      prKet' KetZero s "left" _ num  = "000" ++ show num ++ s ++ "000" 
      prKet' KetZero s "right" _ num = "000" ++ s ++ show num ++ "000"
      prKet' (a :+: b) s dir index num
        | dir == "right" && index == a    = prKet' b s dir index (num + 1)
        | dir == "right" && index == 0    = prKet' (a :+: b) (s ++ "(" ++ show num ++ ")") "left" (index + 1) 0
        | dir == "right"                  = prKet' (a :+: b) (s ++ show num) "left" (index + 1) 0 
        | dir == "left"  && index == (-a) = prKet' b s dir index (num + 1)
        | otherwise                       = prKet' (a :+: b) (show num ++ s) "right" index 0 

ksort :: Ord a => Ket a -> Ket a
ksort KetZero = KetZero
ksort (x :+: xs) = ksort (smaller xs) +++ (x :+: KetZero) +++ ksort (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if y < x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if y >= x then larger' ys (y :+: s) else larger' ys s

ksort' :: (Num a, Ord a) => Ket a -> Ket a
ksort' KetZero = KetZero
ksort' (x :+: xs) = ksort' (smaller xs) +++ (x :+: KetZero) +++ ksort' (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if abs y < abs x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if abs y >= abs x then larger' ys (y :+: s) else larger' ys s
reverse1 :: Ket a -> Ket a
reverse1 x = reverse' x KetZero
reverse' KetZero s = s
reverse' (y :+: ys) s = reverse' ys (y :+: s)

なお、上記のプログラムで、ksortに変更がある。それは、reverse1を用いている部分であるが、これは、出てきた順番を保つためである。ksort'では、絶対値での昇順に並べ替える。先に述べたように、生成関数を0から始めて、絶対値での昇順に並べ替えるが、その時、絶対値が同じものでは元の数での昇順になっていてほしい。そのためには、ksortで出てきた順番を守る必要がある。そのため、ksortが変更されている。それではプログラムを実行してみよう。

Prelude> :load "Ket.hs"
[1 of 1] Compiling Ket              ( Ket.hs, interpreted )
Ok, modules loaded: Ket.
*Ket> let a = 4 :+: 5 :+: 3 :+: (-1) :+: (3) :+: 2 :+: KetZero 
*Ket> a
a4^a5^a3^a-1^a3^a2^| ...00(0)00... >
*Ket> prKet a
"|...00000001(0)01211000...>"

７．６　プログラム全体

それでは、プログラム全体をお見せしよう。

{-#LANGUAGE GADTs #-}

module Ket (Ket (KetZero, (:+:)), (+^), (-^), prKet) where

infixr 5 :+:

--data Ket a  = KetZero | a :+: Ket a deriving (Show, Read, Eq, Ord)

data Ket a where
  KetZero :: Ket a
  (:+:) :: a -> Ket a -> Ket a

infixr 5 +^
(+^) :: a -> Ket a -> Ket a
(+^) a b = a :+: b

infixr 5 -^
(-^) :: (Eq a, Ord a) => a -> Ket a -> Ket a
(-^) a b 
  | b == c = error "Nothing (0)"
  | otherwise = c 
    where
      c = delete a b
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 

{-
infixr 5 -^
(-^) :: (Eq a, Ord a) => a -> Ket a -> Maybe (Ket a)
(-^) a b 
  | b == c = Nothing
  | otherwise = Just c 
    where
      c = delete a b
      delete :: (Eq a) => a -> Ket a -> Ket a
      delete a KetZero = KetZero
      delete a (x :+: xs) 
        | a == x = xs 
        | otherwise = x :+: delete a xs 
-}

instance (Eq a, Ord a) => Eq (Ket a)  where
    KetZero == KetZero = True
    KetZero == _ = False
    _ == KetZero = False
    (a :+: b) == (c :+: d) = (a == c) && (b == d)

instance (Show a, Read a, Eq a, Ord a) => Show (Ket a)  where
    showsPrec _ KetZero   = showString "| ...00(0)00... >"
    showsPrec n (a :+: b)   = showString "a" . showsPrec n a . showString "^" . showsPrec n b

prKet :: (Eq a, Ord a, Num a, Show a) => Ket a -> String
prKet KetZero = "|...000(0)000...>"
prKet a = "|..." ++ prKet' (ksort' $ ksort a) [] "right" 0 0 ++ "...>"
    where
      prKet' :: (Eq a, Ord a, Num a, Show a) => Ket a -> String -> String -> a -> a -> String
      prKet' KetZero _ _ 0 num  = "000" ++ "(" ++ show num ++ ")" ++ "000" 
      prKet' KetZero s "left" _ num  = "000" ++ show num ++ s ++ "000" 
      prKet' KetZero s "right" _ num = "000" ++ s ++ show num ++ "000"
      prKet' (a :+: b) s dir index num
        | dir == "right" && index == a    = prKet' b s dir index (num + 1)
        | dir == "right" && index == 0    = prKet' (a :+: b) (s ++ "(" ++ show num ++ ")") "left" (index + 1) 0
        | dir == "right"                  = prKet' (a :+: b) (s ++ show num) "left" (index + 1) 0 
        | dir == "left"  && index == (-a) = prKet' b s dir index (num + 1)
        | otherwise                       = prKet' (a :+: b) (show num ++ s) "right" index 0 

ksort :: Ord a => Ket a -> Ket a
ksort KetZero = KetZero
ksort (x :+: xs) = ksort (smaller xs) +++ (x :+: KetZero) +++ ksort (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if y < x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if y >= x then larger' ys (y :+: s) else larger' ys s

ksort' :: (Num a, Ord a) => Ket a -> Ket a
ksort' KetZero = KetZero
ksort' (x :+: xs) = ksort' (smaller xs) +++ (x :+: KetZero) +++ ksort' (larger xs)
    where 
      smaller xs = smaller' xs KetZero
      smaller' KetZero s    = reverse1 s 
      smaller' (y :+: ys) s = if abs y < abs x then smaller' ys (y :+: s) else smaller' ys s 
      larger xs  = larger' xs KetZero
      larger'  KetZero s    = reverse1 s
      larger'  (y :+: ys) s = if abs y >= abs x then larger' ys (y :+: s) else larger' ys s

infixr 5 +++
(+++) :: Ket a -> Ket a -> Ket a
(+++) a b = connect a b
    where 
      connect KetZero b = b
      connect (x :+: xs) b = x :+: connect xs b 

reverse1 :: Ket a -> Ket a
reverse1 x = reverse' x KetZero
    where
      reverse' KetZero s = s
      reverse' (y :+: ys) s = reverse' ys (y :+: s)