圏論での積と余積―デカルト積

５．４　積の圏

１）デカルト積

デカルト積(Cartesian product)は、直積集合、直積、積集合などと呼ばれたりする。これは集合の集まりに対して、それぞれの集合からひとつずつ元を取り出して組にしたものである。

例えば、二つの集合\(A,B\)に対し、それらのデカルト積\( A \times B \)とは、それらの任意の元\(a \in A, b \in B\)の順序対\((a,b)\)の全てにより構成される集合をいう。

一般には、\(n\)個の集合\(A_i, i=1..n\)に対して定義され、任意の元\(a_i \in A_i, i=1..n\)の順序対\((a_1,a_2,..,a_n)\)のすべてにより構成される集合をいうが、ここでは、話を簡単にするため、二つの集合ということにする。

デカルト積をよく見かける例は座標点である。\(x\)軸上の値\(x_1\)と\(y\)軸上の値\(y_1\)によって、座標点は\((x_1,y_1)\)と表される。

トランプもデカルト積となる。余談だがトランプは和製英語。とかく話題の尽きない大統領もトランプだ。そのスペルはTrumpである。普通名詞のTrumpは切り札、奥の手、素晴らしい人という意味だ。そうであってくれればいいと思う。さて、話を元に戻そう。横軸をランクに、縦軸をスーツにすると、それぞれの交点にカードが一枚対応する。

例えば、ランクが4で、スーツがハートのところにおかれたカードは（4,💛）である。

思わず例にあげそうになったのが、商品ごとに出ているスーパーの価格表。（サンマ、189円）、（さば、250円）などと表示されている。ここまで例にあげた組と同じ構造を取っている。しかし、価格の方の元を考えるのが難しい。整数としたとしても、任意の商品と任意の価格の組は何を表すのだろうか。現実問題として、全ての組が存在することは考えにくい。

僕が通っていた中学では、期末試験が終了すると親との面談に備えて、クラス担任の先生が成績表を用意した。クラス全員の成績が記された表を見せられることは現在ではないと思うが、その当時の親たちはどのような思いで面談に臨んでいたのだろう。成績表は、縦軸を総合成績での順位に、横軸を科目名(この当時は9科目あった)にし、各こま(セル)には点数が記入されていた。
\begin{array}{|c|c|c|c|c|c|c|}
\hline
& 国語 & 数学 & ... & 体育 & 英語 & 合計点 \\
\hline
1 & 98 & 100 & ... & 100 & 95 & 852 \\
\hline
2 & 95 & 85 & ... & 95 & 100 & 833 \\
\hline
3 & 90 & 90 & ... & 98 & 87 & 802 \\
\hline
.. & ... & ... & ... & ... & ... & ... \\
\hline
\end{array}

当時は、コンピュータはおろか電卓もなかったのでソロバンで計算し、コピー機も発明されていなかったのでガリ版だった。先生は何日も夜なべして作成したのではと思う。当時は当たり前のように考えていたが、その時の先生は大変だったなあとつくづく思う。今さらながら感謝だ。ところで、ここでできた表はデカルト積だろうか。組になっていないので、残念ながら、そうではない。それでは、各セルのところに、情報としては冗長なのだが、(国語,1,98),(数学,2,85)などとしたらどうであろうか。何となく、デカルト積のようには見えないだろうか。冗長な情報が付加されたデカルト積のようには見えないだろうか。

それでは、デカルト積を圏論ではどのように表しているかを紹介しよう。デカルト積は下図のようにあらわすことができる。この図で、\(A\)と\(B\)は対象である。また、\(C\)は、\(A\)と\(B\)から構成されたデカルト積である。\(p\)と\(q\)は射である。\(p\)はデカルト積\(C\)の構成要素である\(A\)を示す。\(q\)はもう一方の構成要素である\(B\)を示す。

トランプの場合は、\(A\)はランクであり、\(B\)はスーツであり、\(C\)はカードである。一枚のカードが与えられたとき、それに\(p\)を作用させるとランクが得られ、\(q\)だとスーツが得られる。

Haskellでは、デカルト積は対を用いて表すことができる。例えば、一方の対象を整数\(Int\)、他方の対象をブール値\(Bool\)としたとき、デカルト積は\((Int,Bool)\)となる。そして、\(p\)は対の最初の要素を出力する\(fst\)であり、\(q\)は2番目の要素を出力する\(snd\)である。
簡単な実行例を見てみよう。aでデカルト積の値を一つ定め、これにfst,sndを作用させるだけのものだ。

Prelude> let a = (3::Int,True)
Prelude> :t a
a :: (Int, Bool)
Prelude> fst a
3
Prelude> snd a
True

デカルト積の基本形だけだと面白みがまったくと言っていいほどない。昨日、「総合診療医ドクターGスペシャル」という番組を見ていたら、肺がん治療法についてディスカッションしていた。がんはその周りを大きく切除した方が転移を起こす危険が減るそうだ。しかし、肺がんの場合、あまり大きく切ると呼吸困難に陥るというリスクが伴う。そこで、最小限の範囲で切除することが求められるそうである。

実は、デカルト積にもこれと同じような性質が要求される。先に挙げた図において、デカルト積はこれ以上余分な情報が含まれていないというところまで、切り刻んだものである。

従って、余分なものを含んだものから最小のデカルト積を得るための工程を示したのが、下図である。\(C'\)は\(A\)と\(B\)から構成されたデカルト積に余分な情報を組み込んだ対象である。\(m\)が余分な情報を除くための射である。\(p'\)は\(C'\)から\(A\)への射で、\(q'\)は\(B\)への射である。また、\(p'=p \circ m\)であり\(q'=q \circ m\)である。

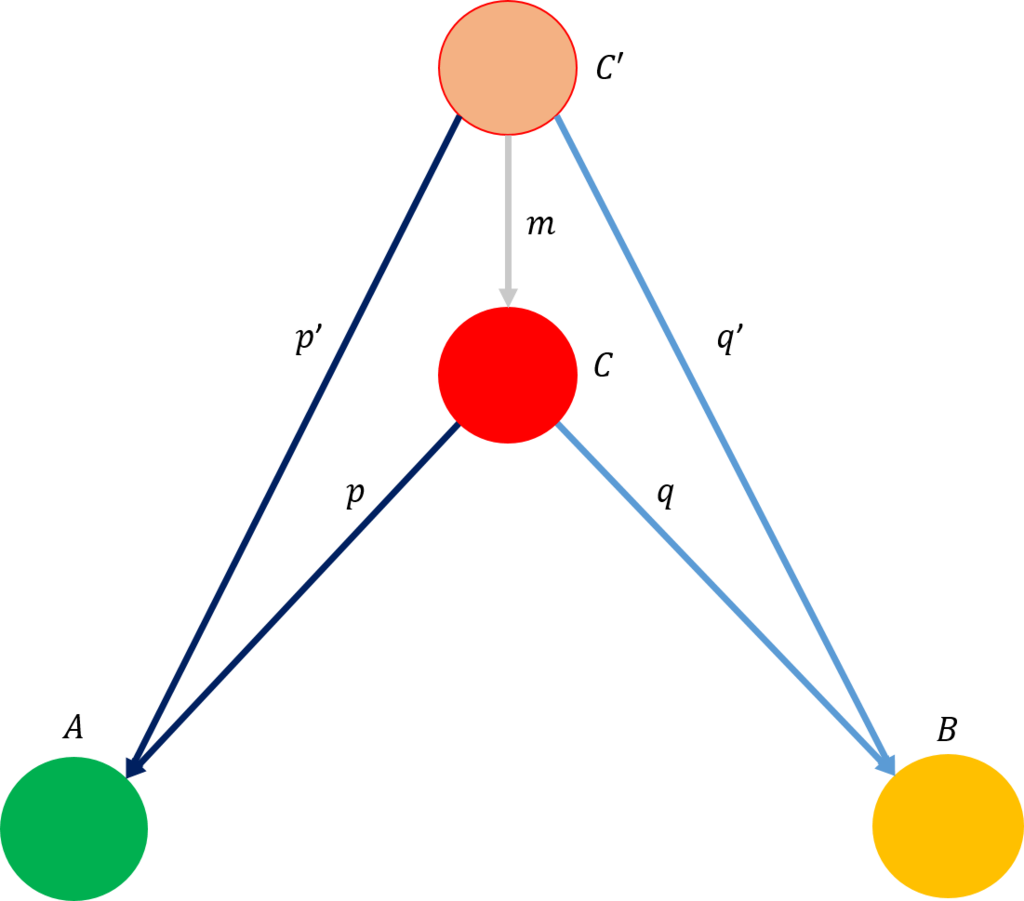
それでは、先ほどの成績表を考えてみよう。対象は科目名\(Subject\)、順位\(Rank\)、成績\(Mark\)とし、デカルト積を対象\((Subject,Rank)\)とし、余分な情報を含んだ対象を\((Subject,Rank,Mark)\)とする。\(p,q\)はそれぞれ\(fst,snd\)となり、\(p',q'\)もそれぞれ\(fst,snd\)となる。また、\(m\)は3番目の対象を除く射となる。すなわち、\(m:(Subject,Rank,Mark)\rightarrow(Subject,Rank)\)である。

これをHaskellで実装すると以下のようになる。

Prelude> data Subject = Kokugo | Sugaku | Rika | Shakai | Ongaku | Bijyutu | Kateika | Taiiku | Eigo deriving (Eq, Show, Read)
Prelude> type Rank = Int
Prelude> type Mark = Int
Prelude> let p = fst
Prelude> let q = snd
Prelude> let m (s, m, _) = (s,m)
Prelude> let p' = p . m
Prelude> let q' = q . m
Prelude> let a = (Kokugo :: Subject, 1 :: Rank, 100 :: Mark)
Prelude> p' a
Kokugo
Prelude> q' a
1
Prelude> m a
(Kokugo,1)

２）最大公約数

数学には積と呼ばれるものがたくさんある。これらの積でも、デカルト積で論じた概念と同じ性質は存在しないのだろうか。もし、このようなものが存在するとすれば、これは積と呼ばれるものすべてに通じる普遍性となる。

デカルト積で説明した性質は次の図である。

この図で、\(p'=p \circ m\)であり\(q'=q \circ m\)である。これから、公約数もこの図で表されることを示すが、この図はより一般的な図なので、積を表す圏と呼ぶことにする。

今二つの整数\(a,b\)を考えよう。これら整数は約数をもつ。
例えば、\(a=66,b=72\)の時、\(a\)の約数は2,3,6,11,22,33であり、\(b\)の約数は2,3,4,6,8,12,24,36である。
これら二つの整数に共通な約数は2,3,6である。
これを\(c=6,c'=3,c"=2,...\)として上の図に記入してみよう。

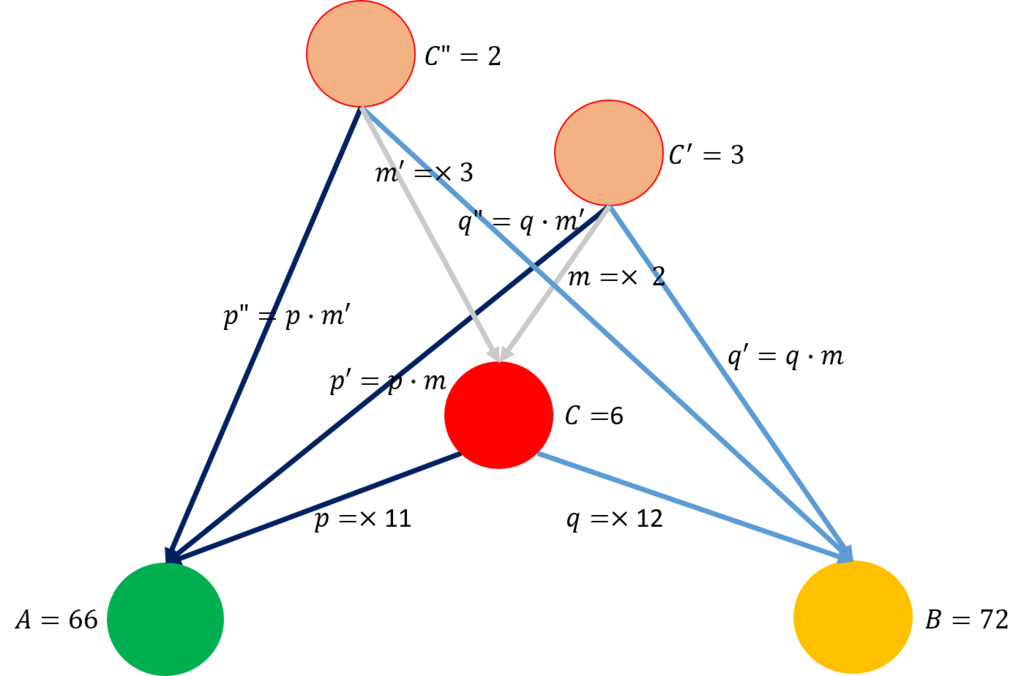
さて上の図のピンクと赤で示した対象の間にはどのような関係があるのだろう。成績表を説明しているときは、ピンクは冗長な情報を有しているとし、冗長な情報をそぎ落としたのが、赤であると説明した。何となくわかったようにさせてくれるレトリックな表現で、数学的な厳密性を欠いている。成績表と公約数の両方のケースを、さらには、積と呼ばれる一般的な圏に対して、共通に説明できる用語で表現することを考えよう。

まず成績表の方から考えてみよう。ピンクの方は(a,b,c)という3組で表される。赤の方は(a,b)という2組で表されている。それぞれが持つ情報の精度という視点から比較すると、ピンクの方がより詳しいといえる。情報が表している空間を考えると、ピンクが表している領域は、赤のそれに含まれることが分かる。即ち、\(pink \subset red\)となる。

次に公約数の方を考えてみよう。公約数は、素因数に分解することができる。例えば、ピンクの\(C'=3\)は素因数分解すると(3)である。他方、赤の\(C'=6\)は素因数分解すると(2,3)である。これを素因数の集合と考えると、いずれのピンクに対しても\(pink \subset red\)となる。

このことから、赤はピンクの領域を可能な限り拡げたものと考えることができる。従って、公約数の場合、赤での公約数は最大公約数となる。

上の図では一つの最大公約数について示したが、これが圏であるといわれても、困る人が多いことと思う。それで、下図のように一般化しよう。

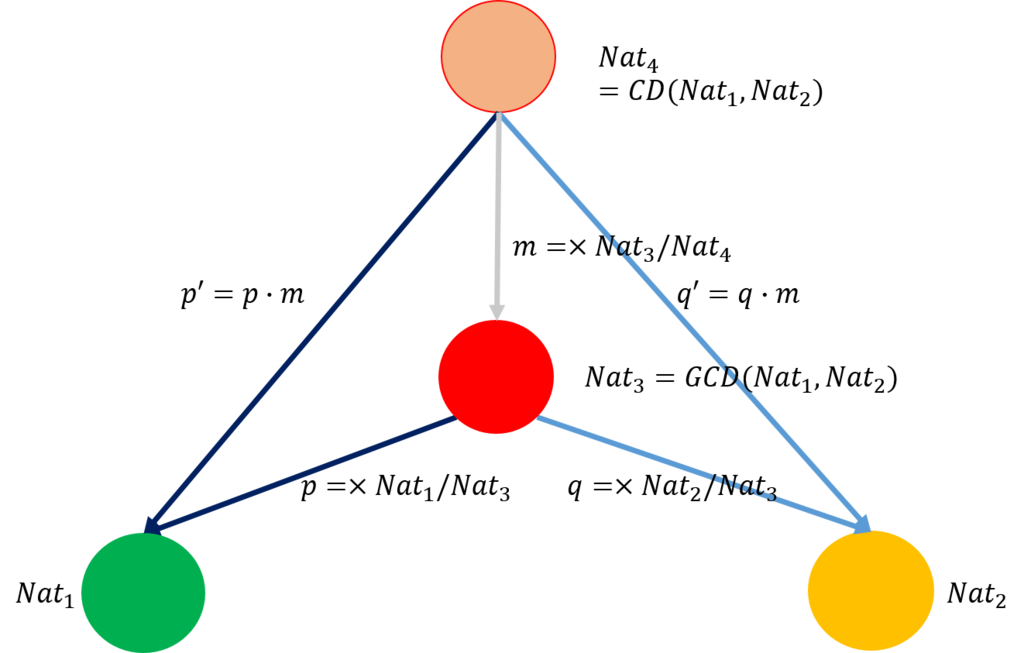
上の図で、\(A\)(緑)\(B\)(黄)はともに1で始まる自然数\(Nat\)で構成される対象である。\(C\)(赤)は、\(A,B\)の最大公約数で構成される対象である。また、\(C'\)(ピンク)は、\(A,B\)の約数で構成される対象である(図では約数を求める関数は\(CD\)となっている)。射\(p\)は乗算する関数で、乗算する数は\(A\)の値を\(C\)の値で割ったものである。同様に、射\(q\)も乗算する関数で、乗算する数は\(B\)の値を\(C\)の値で割ったものである。射\(m\)も乗算する関数で、乗算する数は\(C\)の値を\(C'\)の値で割ったものである。また、\(p'=p \circ m,q'= q \circ m\)である。このことから。上の図はデカルト積の圏と同じ構造を有していることが分かる。

ウィキペディアで積(圏論)を調べると例が出てくる。その最後に、「半順序集合は順序関係を射として用いることで圏として扱うことができる。この場合積と余積は最大下界と最小上界（交わりと結び）に対応する」というのがある。最大公約数はここで述べられている最大下界に相当するものである。

３）論理積

論理積も同じように積の圏として考えることができる。ここでは、図のみを示すので、これをもとに考えて欲しい。

ここの部分はウィキペディアで積(圏論)の例で、「位相空間の圏における積は、各因子の台集合のデカルト積を台として積位相を入れた空間である。積位相はすべての射影が連続であるような最も粗い位相である」に相当する部分である。

４）積の圏

最後に積の圏(product category)をまとめておこう。再び次の図を使う。

積の圏とは、上の図が可換図式となるような対象\(C\)、射\(p,q\)、対象\(A,B\)が存在し、さらに、一意的な関数\(m\)が存在して、その他の対象\(C'\)に対して、\(m: C' \rightarrow C\)となる。
即ち次のようになる。
1) 積と呼ばれる対象が一つ存在する。これを\(C\)とする。
2) \(C\)には投影(projection)と呼ばれる二つの射\(p,q\)が存在する。これらは\(C\)をそれぞれ\(A,B\)に投射する。
3) \(C\)以外の任意の対象\(C'\)は\(A,B\)へ投影する射\(p',q'\)を持つ。そして、ただ一つの射\(m\)が存在し、これは\(p'=p \circ m,q'= q \circ m\)を満たす。

\(C\)が上記を満たす時、これは\(A,B\)の積と呼ばれ\(C=A \times B\)と記される。