6.9 反関手
以前に、\(Reader\)と呼ばれる関手について説明したことがある。二つの射を得て一つの射を出力するという分かりにくい関手だったのではと想像している。圏論は、射を中心にして考えるので、射を射の入力や出力として利用するのは自然なのだが、値で慣れている場合には頭の切り替えが必要になり、分かりにくいことと思う。
そこで、\(Reader\)の復習をした後で、反関手の話をしよう。
1)射を関手にする―復習
具体的な例を用いて、前に説明したファンクタ\(Reader\)を再度考えてみる。そのため、次の問題を考えてみよう。
【問題】苗字という概念がなかったある地域\(\mathcal{C}\)で名前の文字数をカウントする関数\(f\)が用いられていたとしよう。この地域と交流のあった別の地域\(\mathcal{D}\)に、様々な技術移転が生じ、文字数をカウントする関数も他のものと一緒に移転された。しかし、\(\mathcal{D}\)での名前は氏や階級などが一緒になった複雑な構造をなしていた。数学の得意な人がいろいろと考えて、複雑な構造の名前から「名」の部分を取り出す関数\(g\)を考え出した。\(\mathcal{D}\)での名前から名の部分の文字数を得るためにはどうしたらよいかを関手を用いて説明しなさいというのがこの問題である。
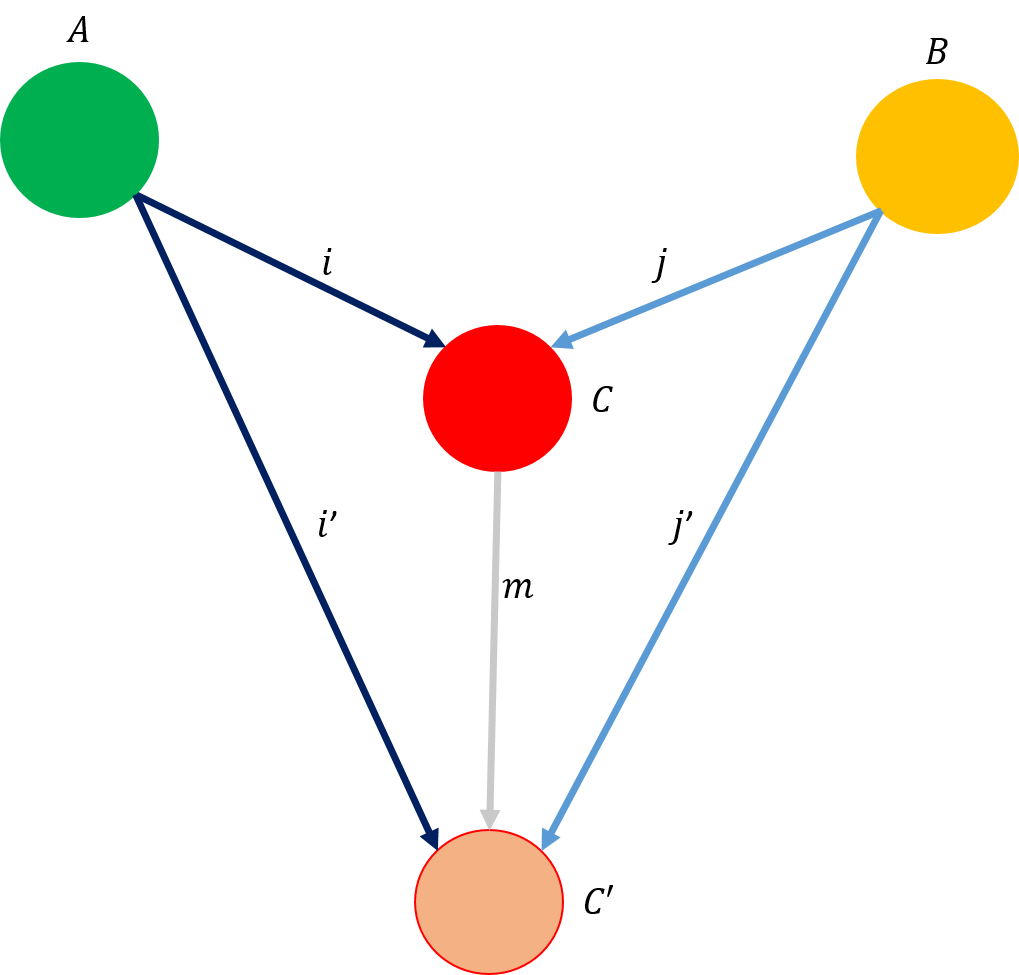
それぞれの地域を圏とし、それぞれの圏の構成を下図に示す。

\(\mathcal{C}\)では、名前を対象\(A\)で文字数を対象\(B\)で表わした。また、名前から文字数に変換する射はそのまま\(f\)である。\(\mathcal{C}\)の対象と射は関手\(F\)によって\(\mathcal{D}\)に移される。即ち、\(\mathcal{C}\)の\(A,B\)は\(F(A),F(B)\)に移され、\(f\)は\(F(f)\)に移されている。
複雑な構造の名前の対象は\(F(R)\)で表した(これは、\(\mathcal{C}\)の対象\(R\)を\(\mathcal{D}\)に移したと読める。このように意図しているのだが、\(\mathcal{C}\)にはもしかすると\(R\)は存在しないかもしれない。この問題の場合には明らかに存在しないのだ。従って、ここでは、この国の名前は\(F(R)\)であるという程度に考えて欲しい。\(F\)がついている理由はHaskellのプログラムになった時に分かる)。(同じ理由から)複雑な名前から名に変換する射を\(F(g)\)とした。ここで、求めたいのが、\(F(R)\)から\(F(B)\)への写像である。これは次のようになる。

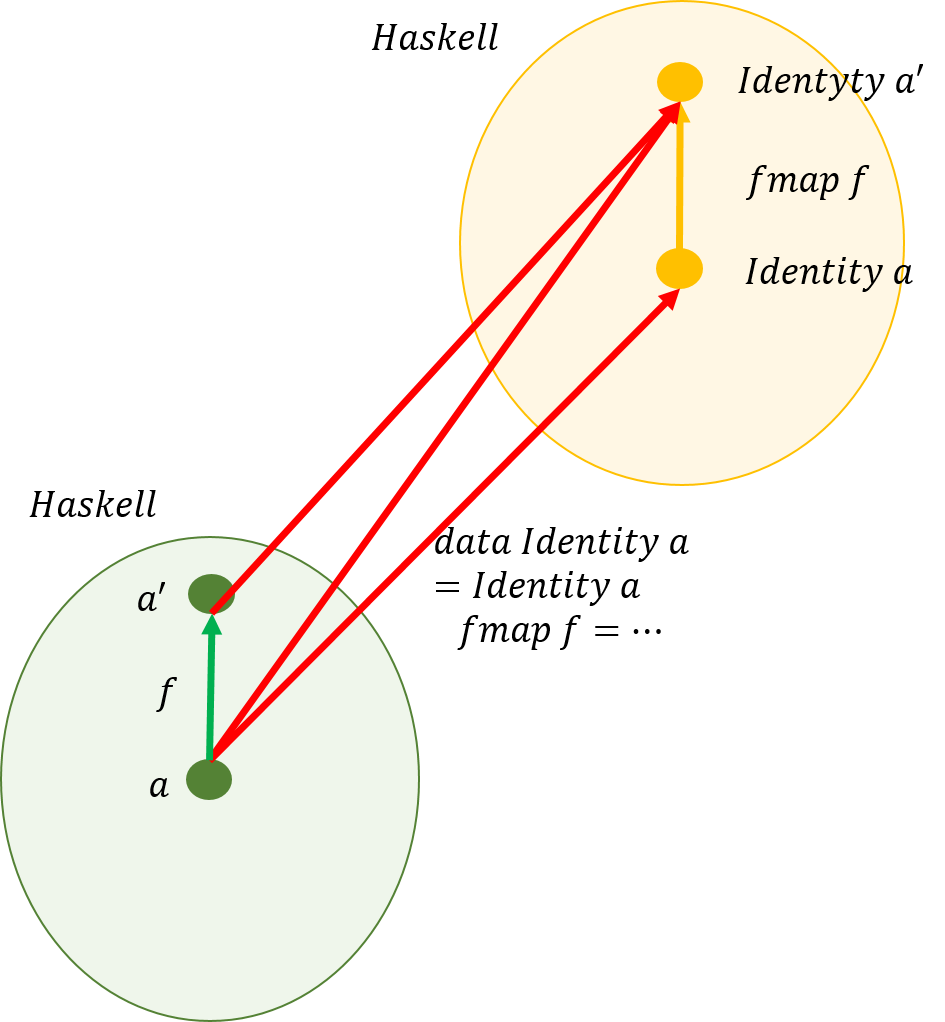
圏でのこの関係をHaskellで記述すると次のようになる。

具体的にプログラムで記述すると、
{-# LANGUAGE InstanceSigs #-}
newtype Reader r a = Reader { getName :: r -> a }
instance Functor (Reader r) where
fmap :: (a -> b) -> Reader r a -> Reader r b
fmap f (Reader g) = Reader (f.g)
first :: (a,a,a) -> a
first (a,_,_) = a
count :: Reader (String, String, String) Int
count = fmap (length :: String -> Int) (Reader first)
smap =[("Takuya","Omi","Kimura"),("Goro","Muraji","Inagaki"),("Hiroaki","Tomonomiyakko","Nakai"),("Singo","Agatanusi","Katori")]このプログラムで\(count\)が\(Reader \ r \ r\)即ち\(F(r)\)から\(Reader \ r \ b\)即ち\(F(b)\)への射を出力してくれる。そこで、データ型(\(Reader \ r \ a\))で定義されているフィールド\(getName\)を利用して射\(r \rightarrow a\)を取り出す。ここで取り出される射は\(r\)から\(b\)への関数である。
これに、複雑な構造の名前(といっても、ここでは、ファーストネームと氏姓制度での地位とラストネームからなるトリプルだが)を入力に与えると、その文字数を与えてくれる。なお、名を散りだす関数は\(first\)である。これは、トリプルの最初の要素を取り出す。
最初の実行例は個人名を与えたものである。\(count\)は\(F(r)\)から\(F(b)\)への射を与える。これに、\(getName\)を施すと\(r\)から\(b\)への射\(length.first)\)を与える。これに("Mike", "Omuraji", "Brooks")という名前を与えてるとファーストネームの文字数が出力される(因みに、友人のMike Brooksは現在は学長だ。「大連」より偉いかもしれない)。少し、複雑だがこのプログラムはこのようになっている。
次は、あるグループを構成していた人たちの名前を入力とした。<$>もファンクタの一種だが、配列での適応を可能にしてくれる。
*Main> getName count ("Mike","Omuraji","Brooks")
4
*Main> getName count <$> smap
[6,4,7,5]*Main> getEven even' "Taro" True *Main> getEven even' <$> smap' [True,True,False,False]
データ型\(Reader\)は関数を表現しているので、関数型(Function Type)とも呼ばれる。
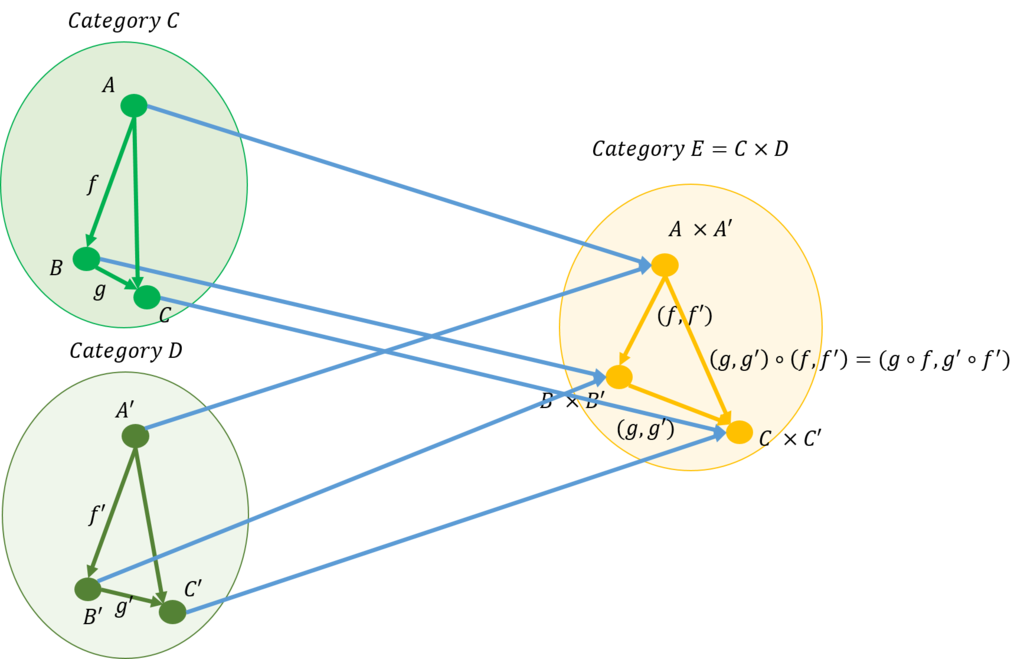
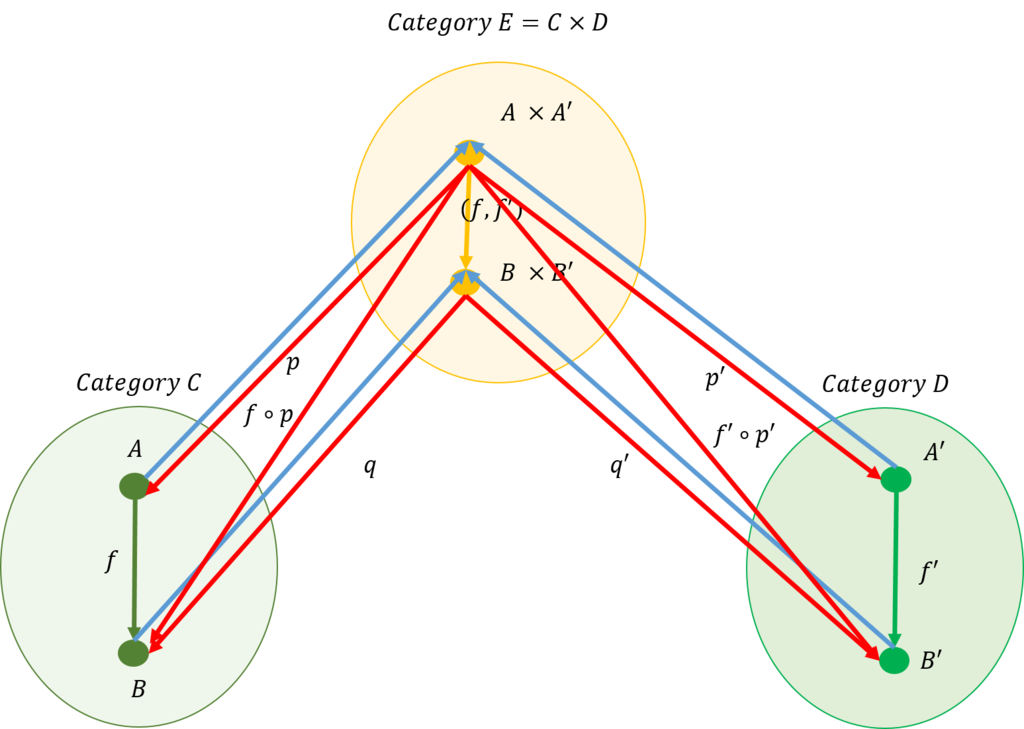
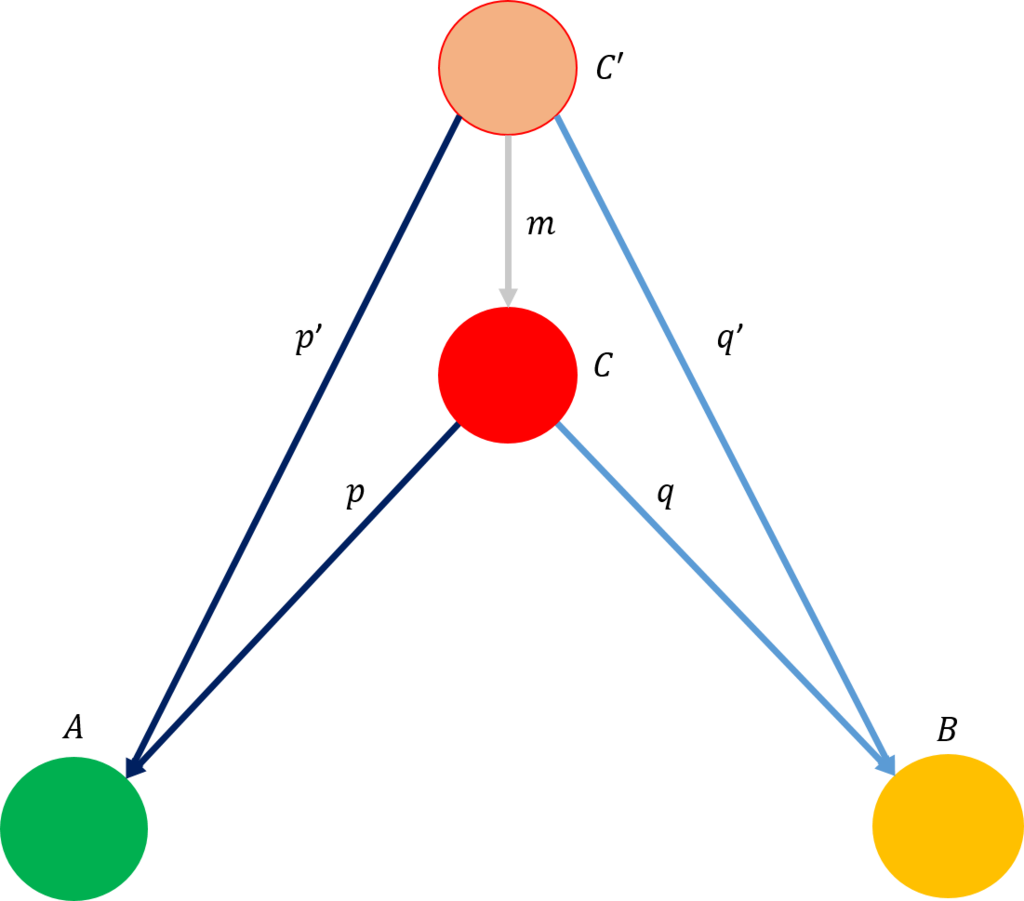
圏での表現を書き換えると下図のように表すこともできる。

この図から、\(\mathcal{C} \times \mathcal{D}=\mathcal{D}\)であることから、デカルト積になっていることもわかる。
2)反関手
それでは先ほどの文字数を求める問題にもう一度戻ることにしよう。
【問題】さらに別の地域\(E\)があって、そこでは文字数が偶数であるかどうかを判断していたとする。
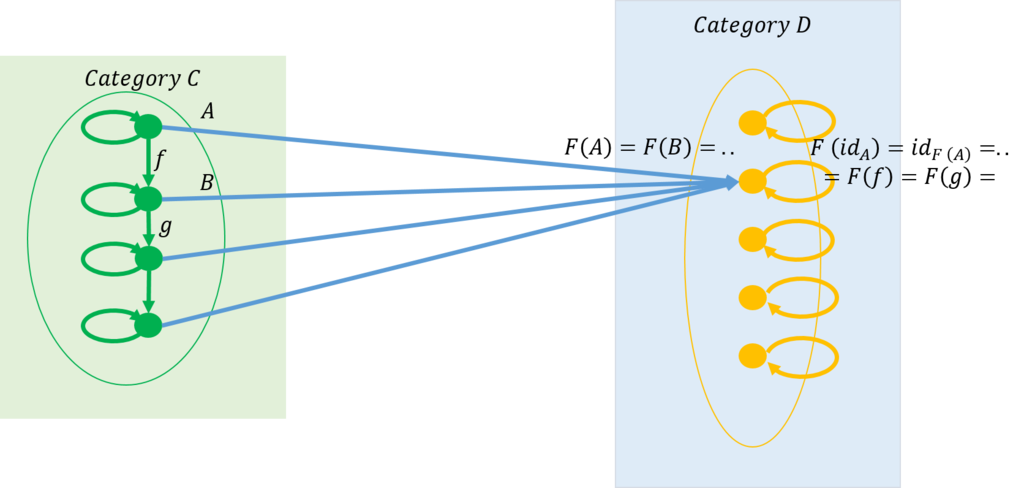
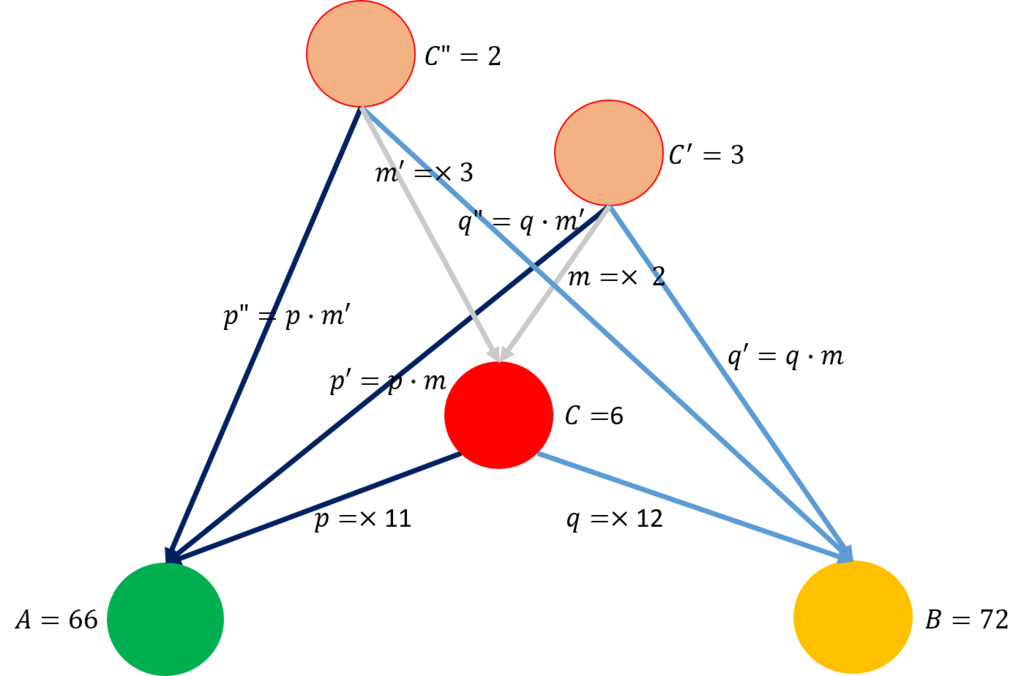
取り敢えず\(C,E\)を圏にして図を示すことにしよう。

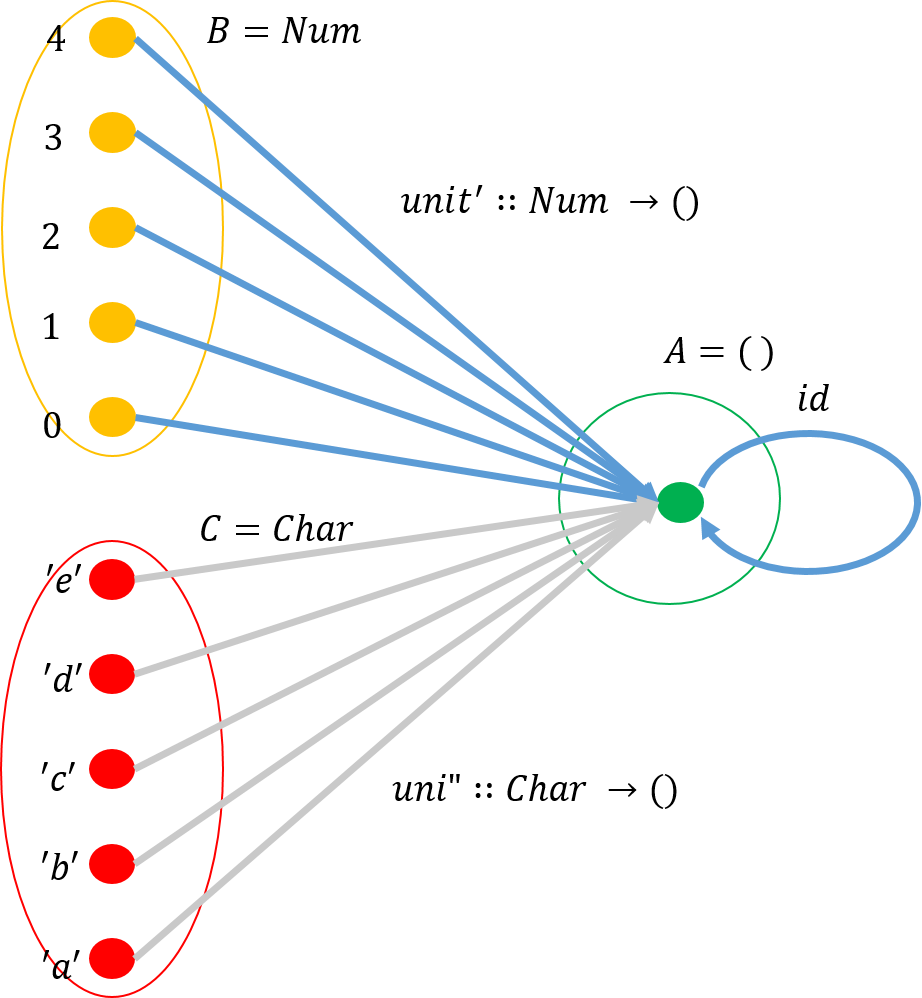
ここで、\(f\)は\(A\)から\(B\)に写像する。それにもかかわらず、矢印の方向は\(F(B)\)から\(F(A)\)である。同様に\(g\)は\(B\)から\(C\)に写像するが、矢印の方向は\(F(C)\)から\(F(B)\)である。このように、ドメイン側の圏\(C\)の全ての射に対して、コドメイン側の圏\(E\)ではその方向が逆になるものを反関手(\(Contravariant\)あるいは\(Cofunctor\))と呼ぶ。
方向が逆向きになることを説明する。今回も前回と同じように、射を利用して、関手を張ることとする。前回は\(Reader\)という関手であった。これは\( new type \)を利用してデータ型を定義したが、その時のデータ型は\(Reader \ r \ a = Reader \ r \rightarrow a\)であった。
その時、\(r\)の方は固定して\(a\)の方が変われるようにした。\(Reader \ r \ a\)は、\(r\)を入力とし、\(a\)を出力とすると考えることができる。従って、データ型の\(Reader \ r \ a\)とフィールドで定義した\(r \rightarrow a\)とは方向が同じと見なせる。
次に、これから説明しようとするものは、反関手\(Writer \ c\)で張られる。後で示すが、そのデータ型は、\(Writer \ c \ a = Writer \ a \rightarrow c\)である。これは、前者\(Reader\)が射の入力を固定したのに対し、後者\(Writer \)は射の出力を固定するためである。このため、\(Writer \ c \ a\)は\(c\)を入力とし、\(a\)を出力とするようにふるまう。これに対して\(Writer \ a \rightarrow c\)は逆である。このため、方向はお互いに逆になる。
さて、本題に移ろう。ここで求めたいのは、\(F(C)\)から\(F(A)\)への射である。下図のようになる。
図
Haskellでの表記に変えると以下のようになる。
図
プログラムは以下のようになる。
{-# LANGUAGE InstanceSigs #-}
class Contravariant f where
contramap :: (a -> b) -> f b -> f a
newtype Writer c a = Writer { getEven :: a -> c }
instance Contravariant (Writer c) where
contramap :: (a -> b) -> Writer c b -> Writer c a
contramap f (Writer g) = Writer (g.f)
even' = contramap (length :: String -> Int) (Writer even)
smap' =["Takuya","Goro","Hiroaki","Singo"]前と同じように実行してみよう。予想通りの動きになっている。
*Main> getEven even' "Taro" True *Main> getEven even' <$> smap' [True,True,False,False]
\(Reader\)の場合と同じようにこれも圏の積になるが、反関手なので、\(C^{op} \times E \rightarrow E \)と記す。\(\mathcal{C}^{op}\)は\(\mathcal{C}\)の全ての矢印を逆にした圏を表す。
次回はいよいよ関手の最後、プロファンクタのお出ましだ。