今年最後に読む本を定めて、28日に市の図書館から網野義彦著『日本の歴史のよみなおし(全)』と山本淳子著『源氏物語の時代 ― 一条天皇と后たちのものがたり』を借りた。
『日本の歴史のよみなおし』は、中世の時代を中心にいくつかのテーマに沿って横断的に説明している。ロングセラーになっている本なので、読まれた方も多いことと思う。2005年に出版されたこの本は、1991年と1996年に刊行された本の合本である。両方とも、筑摩書房の社員向けに講演した内容をもとに書かれている。このため、要領よくまとまっていて読みやすい。

文字、貨幣、女性などがテーマとして取り上げられている。その中で、「日本の社会は農業社会か」を説明した部分が最も感銘を受けた。1991年の山川出版の高校の教科書には、「封建社会では農業が生産の中心で、農民は自給自足の生活を立てていた」と記述されていたそうである。この根拠になっていたのは、関本直太郎著『近代日本の人口構造』である。この中に、秋田藩の人口構成を示した表があり、そこには、諸士9.8%、百姓76.4%、町人7.5%...と示された表がある。
子供の頃、ご飯を残すと「お百姓さんが丹精込めて作ったものを残してはいけない」と叱られた。百姓イコール農民のイメージを持っていたが、この表を利用した学者も百姓を農民と見なしたようである。
能登半島の時国家の文書を調査していた網野さんは、年貢を納めていない百姓が多いことに気がつく。子供の頃に聞いたことのある言葉だが、いわゆる、水呑百姓である。その頃は、この言葉は貧乏な農家を示していた。しかし、網野さんはそうではないことに気がつく。廻船業などで裕福な生活をしている人たちだ。今でいう兼業農家だ。本業は農業以外の職業だが、所有する農地からの生産高がわずかであるために、水呑百姓として分類された人々だ。
このことを発見した網野さんは、封建社会には農業以外の産業に従事している人が多くいたはずだと主張し、この視点からの研究の必要性を説いている。今春、購入した山川出版の『詳説日本史研究』の261ページには身分別人口構成がある。百姓87.3%となっている。やはり、農業と解釈しているように読める。百姓という言葉は、中国語では一般の人民を指す。網野さんも指摘しているが、かつてはそのような意味で使っていたのではないかと思う。
『源氏物語の時代』は、源氏物語が書かれた時代に生きた一条天皇およびその后の定子と彰子の心理状態をあぶりだした本だ。

この時代は摂関政治の最盛期である。一条天皇は、藤原家から政治的な圧力を受けながらも、しなやかに生き抜いていく。定子は中関白家の藤原道隆(みちたか)の娘で才気活発である。彰子は当代一の権力者である藤原道長の娘でおっとりとしたお嬢さんである。
一条天皇は、数え年の7歳で即位し、11歳で結婚する。結婚相手は、いとこの定子14歳である。姉さん女房だが、そういうには二人は若すぎる。姉と弟という関係に近かったのだろう。政略結婚なのだが、一条天皇は定子を熱愛するようになる。定子の兄である伊周(これちか)を含めて、三人は夜を徹して漢詩の知識を競うなど、和やかな生活を享受する。しかし、ヒロインの定子には残酷な悲劇が待ち受けている。伊周が謀反の疑いで配流になり、罪人の家の出としての汚名を背負うこととなる。
一方、天皇の祖父になりたいという欲望を抱く道長は、彰子を12歳で一条天皇の后にする。この時、一条天皇は20歳である。また、二人はいとこである(先ほどの網野さんもいとこ婚だそうだ。そして、なんと彼の両親も、そして義理の両親もいとこ婚だそうだ。少し前の日本では普通だったのだろうか)。
この1年後、定子は24歳で3番目の子供を出産した後、亡くなってしまう。彰子は定子の長男の敦康(あつやす)を、定子が亡くなった1年後に、養子として迎える。この時、彰子は14歳、敦康は2歳であった。継母というには年が若すぎるので、敦康を弟のようにかわいがったのであろう。一条天皇の崩御の後、敦康を東宮にするようにと道長に抗議していることからも、このことがうかがえる。政治の世界は、このような情を許さず、彰子が20歳の時に生んだ敦成(あつひら)が東宮になる。
定子が亡くなった後も、一条天皇は定子が忘れられず、悲しい日々を送っていたようだ。しかし、状況を読み、対応が柔軟であった一条天皇は、仲のよい夫婦として彰子と過ごすようになる。敦成(後一条天皇)を、さらには、敦良(あつなが後朱雀天皇)を儲け、後には、聖代と崇められた。
なお、一条天皇は辞世の句を残している。死ぬ間際のか細い声で言ったため、聞き手によってその内容が異なっている。道長の『御堂関白記』には、
露の身の草の宿りに君を置きて 塵を出でぬることをこそ思へ
となっている。また、藤原行成の『権記』には、
露の身の風の宿りに君を置きて 塵を出でぬることぞ悲しき
となっている。
道長は、当然、「君」は娘の彰子だと思っている。従って、この歌は彰子に捧げたものだと解釈している。これに対して、行成は、「君」は天皇が寵愛していた定子だと解釈している(偶然だが、道長と行成は同じ年の同じ日に亡くなっている)。
作者の山本さんは前者だと思っている。物語の筋としては後者の方が面白そうだが、柔軟に対応した一条天皇であれば前者になるのだろうか。
ところで、草枕の著者である清少納言は定子に、源氏物語の紫式部は彰子に仕えた。この辺りの心理描写も巧みに描かれているので、楽しく読むことができる本である。
5.圏論での積と余積
歴史の中に普遍性を求めることは大変だ。今日の歴史学は多様性を大切にしているので、さらに大変だ。この究極にある学問が数学である。数学は普遍性を追求する学問だといっても過言ではない。その中でも、圏論は最も抽象的であり、最も一般的な普遍性を求めている。これから圏論の中で論ぜられてきたいろいろな普遍的な性質(universal properties)を説明する。まず、手始めに、積(product)と余積(coproduct)から始める。それでは、その一部を構成する始対象と終対象から説明しよう。
5.1 終対象
終対象の定義から始めよう。これは次のように定義される。終対象とは、対象の一つであるがそれは次の性質を持つ。圏内の任意の対象からこの対象への射が一つそして唯一つだけである。
もう少し、詳しく定義してみよう。
ある圏において、一つの対象を\(A\)とする。また、任意の対象を\(B\)とする。この時、下記の①と②を満たすような\(A\)が存在するとき、\(A\)を終対象という。
①\(f:B \rightarrow A\)なる射が存在する。
②任意の二つの射\(f,g:B \rightarrow A\)が存在するとき、\(f=g\)が成り立つ。
例を示そう。

上図で、\(A\)が終対象である。少し調べてみよう。任意の対象となるのは\(A,B\)の二つである。
対象\(A\)から\(A\)への写像\(id\)のみである。これは①と②の条件を満たしている。
また、対象\(B\)から\(A\)への写像は\(f\)のみである。これも①と②の条件を満たしている。
従って、対象\(A\)は終対象となる。
もう一つの例を示そう。Haskellにはタプルがある。例えば、年齢と性別をタプルで示すと\((age,sex)\)となる。このタプルの構成要素は年齢と性別の2個である。構成要素が\(n\)個のものを\(n\)-tuppleという。\(n\)が1以上のものは分かりやすいと思うが、\(n\)が0の場合はどうであろうか。
上述した源氏物語では、年齢を数え年で考えていた。最近は数え年を使わなくなったので、なじみのない人も多いと思う。数え年は誕生したときに1歳となり、その後は、正月を迎えるごとに1歳ずつ増える。これに対して、満年齢は誕生日を迎えるごとに1歳ずつ増え、最初の1年は0歳である。
0という数は、何もないことを表すので、構成要素がない場合には0-tuppleとなる。これは構成要素がないので()と表される。Haskellでは()はシングルトンと呼ばれる。
シングルトンは特殊な対象である。即ち、いかなるタイプの対象からもシングルトンへの射を用意すると、シングルトンは終対象となる。シングルトンへの射を次のように用意しよう。
unit :: a -> () unit _ = ()
実行してみよう。
Prelude Data.Void> :load "unit.hs" [1 of 1] Compiling Main ( unit.hs, interpreted ) Ok, modules loaded: Main. *Main Data.Void> unit 2 () *Main Data.Void> unit 'a' () *Main Data.Void> unit "spring" () *Main Data.Void> unit (14,"male") () *Main Data.Void> unit () ()
最初の例は、対象\(Num\)からシングルトンに写像する唯一の射である。即ち、\(unit :: Num -> ()\)である。図で表すと次のようになる。

2番目の例は、対象Charからシングルトンに写像する唯一の射である。即ち、\(unit :: Char -> ()\)である。
3番目の例は、対象[Char]、即ち、文字列からシングルトンに写像する唯一の射である。即ち、\(unit :: [Char] -> ()\)である。
4番目の例は、対象(Num,[Char])からシングルトンに写像する唯一の射である。即ち、\(unit :: (Num,[Char]) -> ()\)である。
5番目の例は少し注意を要する。図で示すように\(id=unit\)である。

上記の例は、\(A\)に写像される対象が自身を除いて一つ(5番目の例では0)であったが、複数ある場合の例を示そう。
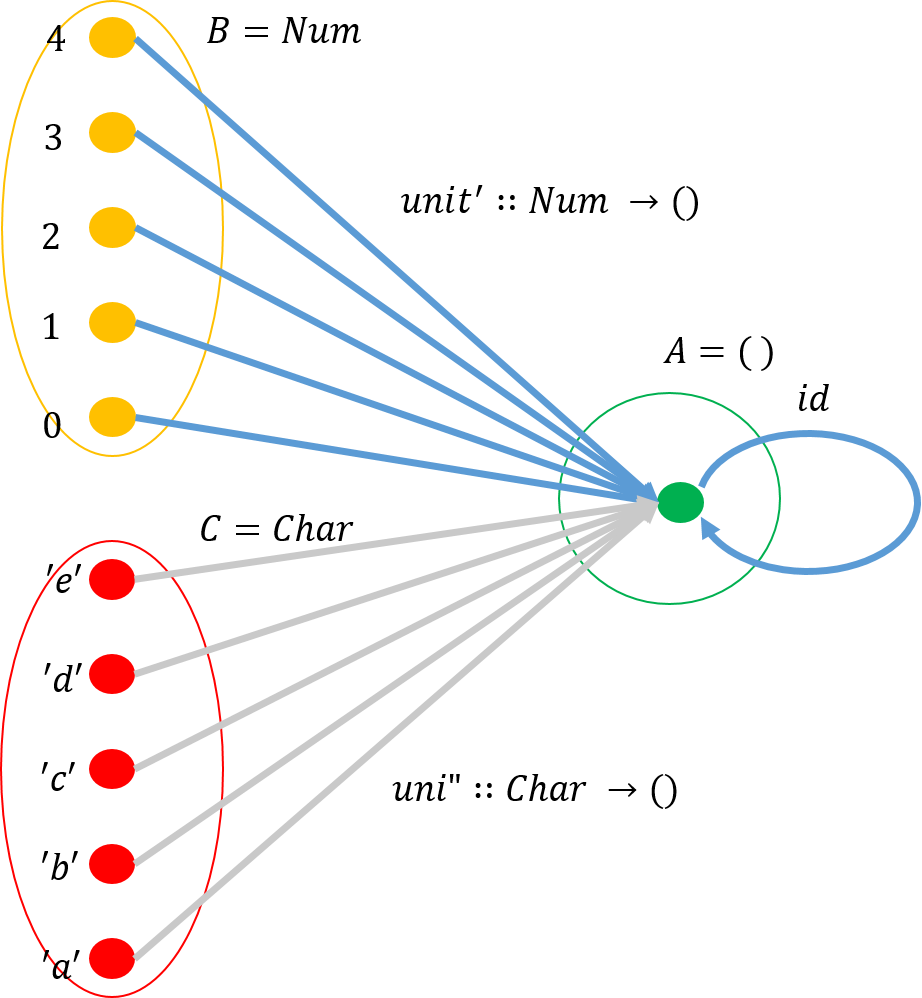
上図では、タイプNumとタイプCharの対象を用意した。分かりやすくするために、射をそれぞれの対象ごとに別々に設け、それぞれをunit',unit"とした。
ところで、終対象は一つとは限らない。複数の場合もある。しかし、この場合でも、それぞれを構成する射の間が同型写像となる(これについては後の記事で説明する)。その結果、これらの終対象を同じものとみなすことができる。
5.2 始対象
始対象次のように定義される。始対象とは、対象の一つであるがそれは次の性質を持つ。この対象から圏内の任意の対象への射が一つそして唯一つだけである。
もう少し、詳しく定義してみよう。
ある圏において、一つの対象を\(A\)とする。また、任意の対象を\(B\)とする。この時、下記の①と②を満たすような\(A\)が存在するとき、\(A\)を始対象という。
①\(f:A \rightarrow B\)なる射が存在する。
②任意の二つの射\(f,g:A \rightarrow B\)が存在するとき、\(f=g\)が成り立つ。
例を示そう。Haskellでは、以前のブログで説明したが、Voidというタイプを用意している。
*Main Data.Void> :i absurd absurd :: Void -> a -- Defined in ‘Data.Void’
これを図で示すと次のようになる。

Voidという用語はC++でも使っているので、混乱を起こす。C++でのvoidは、先ほど説明したスケルトン()と同じである。
先ほどの説明で()は何もないということを表していた。HaskellでのVoidは、空っぽと説明されることが多いが、これでは、()との違いが分からない。適当な日本語がないので、英語を用いるが、HaskellのVoidはPrinciple of explosionである(explosionは爆発を意味する)。即ち、「命題A=>Bの前提条件Aが偽である時、A=>Bは真である」という論理での偽の部分に当たるのが、Voidである。Voidを偽とみなせば、命題absurd :: Void -> aは真であることになる。即ち、前提条件が偽であれば、どのような命題を持ってきたも真となる。言い換えると、矛盾からは何事も引き出せるということになる。とても、比喩的に述べると、ビッグバンが起きるようなものだ。超高温、超高密度な火の塊から宇宙が誕生するような感じだ。
面倒くさい議論になったが、哲学的な説明から離れて、分かりやすい例を示そう。0で始まる自然数を昇順(<)に並べると次のようになる。

昇順で用いた大小関係(<)を射とみなし、対象\(A\)と\(B\)を次のように定めると\(A\)は始対象となる。

先ほどと同じで、始対象についても、複数存在する場合があるが、その場合には、これらは等価であるとみなせる。
ところで上の図で、降順(<)に並べ、射の矢印を逆方向にすると、0は終対象となる。このような性質を双対(Duality)という。

圏には始対象あるいは終対象が存在しない場合がある。圏を構成したときは、どれが始対象になるのか、どれが終対象になるのか、あるいは、なぜ存在しないのかを考えると、圏に対する認識が深まることと思う。